电驱高压气动减压阀动态特性仿真研究

赵祉昕， 高隆隆， 李宝仁

(华中科技大学FESTO气动中心，湖北武汉 430074)

引言

压缩空气由于能源获得方便、无污染、成本低，使得高压气动技术广泛应用于机械工业、国防军事、航天航空等各个领域[1-3]。徐志鹏等[4]研制了一种滑阀先导式高压气动比例减压阀，研究了先导阀预开口形式和环形间隙对减压阀性能的影响;李树勋等[5]针对先导式减压阀不稳定性问题，对先导式减压阀进行了非线性动态模型仿真，研究导阀弹簧刚度、导阀活塞直径以及主阀出口腔体积等参数对减压阀阀后压力的影响；张远深等[6]研究了一种带先导流量稳定器的高压气动减压阀，着重研究先导流量稳定器对减压阀性能的影响; 储景瑞等[7]研究了一种大减压比先导式比例减压阀，着重研究控制腔进气阻尼孔和排气阻尼孔对阀性能的影响。

目前，国内外的研究主要集中在高压先导式减压阀和高压比例减压阀上，本研究设计了一种由直流电机直接驱动的电驱高压气动减压阀，该电驱高压气动减压阀设计输入压力为10～40 MPa，出口压力为0.5～5 MPa，通径为DN15，调压响应时间在0.5 s以内，对调压精度和响应速度要求较高。本研究在数学建模的基础上对电驱高压气动减压阀进行了仿真分析，研究了相关参数对调压精度和响应速度的影响，最终选择了合适的设计参数，实现了电驱高压气动减压阀出口压力快速准确的控制。

1 电驱高压气动减压阀工作原理

图1为所设计的电驱高压气动减压阀的结构简图，该减压阀由直流电机驱动，整体为活塞直动式结构。直流电机的输出轴与螺杆相连接，给予直流电机一定的控制电压，直流电机的输出轴带动螺杆一起旋转，螺杆驱动调压螺母向下运动压缩调压弹簧，调压弹簧进而推动活塞顶开阀芯；高压气体从进气腔进入，经过阀口的节流作用，压力降低从排气腔排出；当排气腔气体作用在活塞上的气压力与调压弹簧施加在主阀活塞上的弹簧力平衡后，主阀口开度不变，排气腔出口压力稳定；若入口压力发生波动时，如压力瞬时升高，排气腔压力也随之升高，作用在活塞下方的气压力增大，破坏了原有的平衡，阀芯在复位弹簧的推动下随着活塞一起向上移动，使阀口开度变小，节流阻力增加，排气腔压力减小，直到活塞达到新的平衡为止，反之同理。

图2为所设计的电驱高压气动减压阀的控制原理图，该减压阀采用PID压力闭环控制的方式，压力传感器检测排气腔气体压力p2，p2与设定压力pz的差值经过PID控制器转换成直流电机的控制电压U，直流电机在控制电压U的作用转动一定的角度θ来调整主阀的开度x，进而控制排气腔的出口压力p2达到设定压力pz。

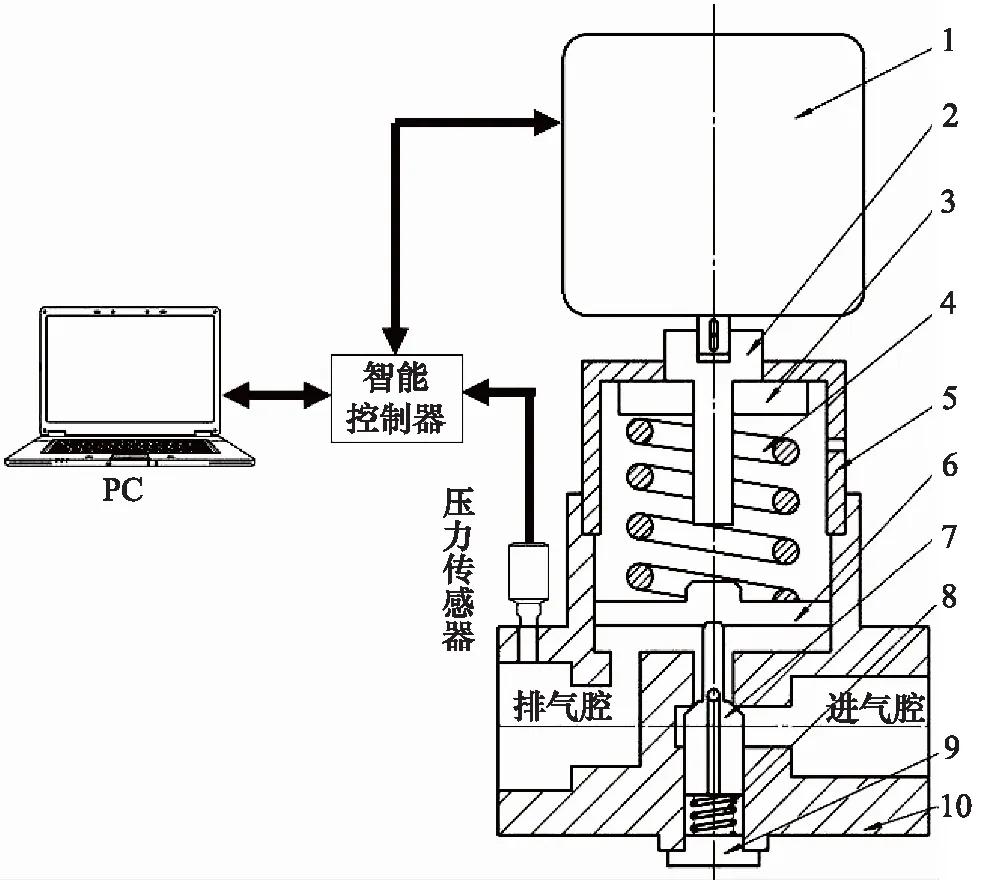
1.直流电机 2.螺杆 3.调压螺母 4.调压弹簧 5.上阀盖6.活塞 7.阀芯 8.阀芯复位弹簧 9.下阀盖 10.阀体图1 电驱高压气动减压阀原理示意图

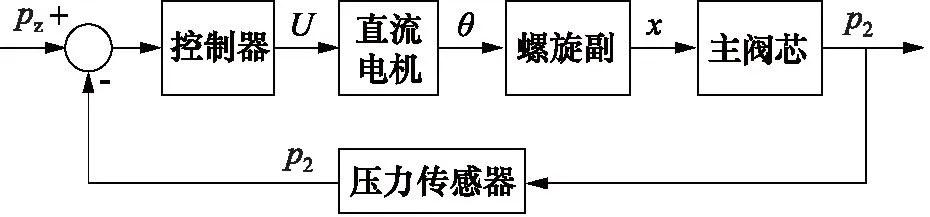
图2 电驱高压气动减压阀控制原理图

2 电驱高压气动减压阀数学模型

在搭建电驱高压气动减压阀的数学模型时，做出如下假设：

(1) 工作介质为理想气体，满足理想气体状态方程；

(2) 气体在减压阀各流道内流动时均为绝热等熵过程；

(3) 减压阀各容腔内温度和压力的分布是均匀的；

(4) 阀排气腔压力与活塞底部压力相等[8]；

(5) 忽略气体泄漏和密封比压的影响。

2.1 直流电机数学模型

对于永磁直流电机[9],有：

(1)

eb=Kbω(t)

(2)

TM(t)=KTi(t)

(3)

(4)

(5)

式中，L—— 线圈电感

i—— 线圈电流

R—— 线圈电阻

ea—— 电机输入电压

eb—— 反电动式

Kb—— 电动机反电动势常数

ω—— 电机转速

TM—— 电机输出力矩

Te—— 负载转矩

KT—— 电机力矩系数

J—— 折算到电机轴上的总转动惯量

B1—— 折算到电机轴上的总黏性阻尼系数

θ—— 电机转过的角度

2.2 阀芯运动组件动力学方程

阀芯运动组件动力学方程如下：

(6)

m=m1+m2

(7)

(8)

式中，m1—— 活塞质量

m2—— 阀芯质量

F1—— 调压弹簧产生的推力

Ff—— 阀芯的摩擦力

Fp—— 排气腔气体作用在活塞上的气压力

F2—— 复位弹簧产生的推力

B2—— 黏性阻尼系数

Fq—— 压缩气体流动产生的气动力

P—— 螺杆螺距

k1—— 调压弹簧刚度

由于气动力与摩擦力的非线性和不确定性，可以把阀芯动力学方程中的Ff与Fp当成干扰忽视[10]。

2.3 阀口质量流量方程

减压阀阀口的高压空气质量流量方程为[11-12]：

(9)

式中，Qm—— 流经阀口的质量流量

Cd—— 流量系数

p1—— 入口压力

k—— 绝热系数

Rg—— 气体常数

T—— 气体温度

σ—— 临界压力比

p2—— 出口压力

2.4 排气腔压力方程

排气腔内气体压力变化为定容积充气和放气同时进行的过程，其压力方程为[13]：

(10)

式中，V—— 排气腔体积

qin—— 进入排气腔气体的质量流量

qout—— 流出排气腔气体的质量流量

3 电驱高压气动减压阀动态特性仿真

3.1 仿真参数设置

仿真模型主要参数设置见表1。

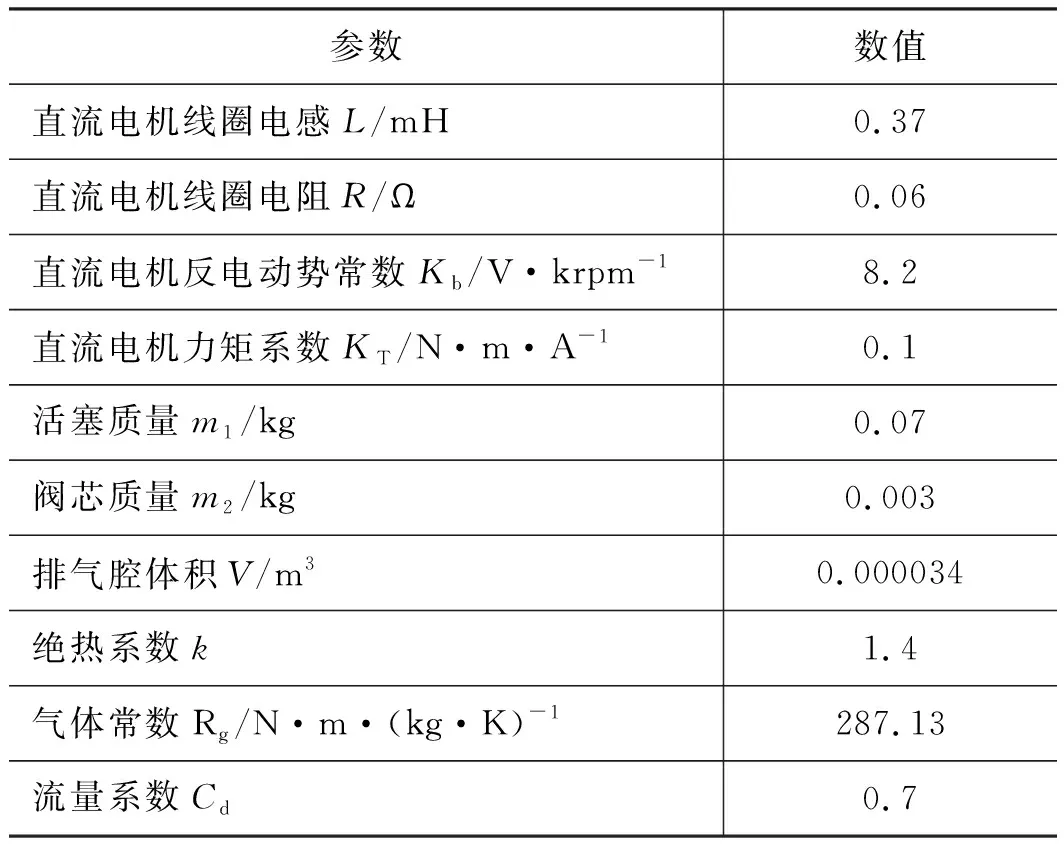
表1 仿真中的主要参数设置

3.2 结构参数对电驱高压气动减压阀性能的影响

基于电驱高压气动减压阀的数学模型，搭建电驱高压气动减压阀的MATLAB/Simulink仿真模型，改变电驱高压气动减压阀的相关参数进行仿真。

1) 不同调压弹簧刚度

设定目标压力pz分别为5 MPa和0.5 MPa，直流电机最高控制电压Umax为18 V，减压阀入口压力p1为40 MPa，改变调压弹簧刚度k1进行仿真分析，仿真结果如图3所示。

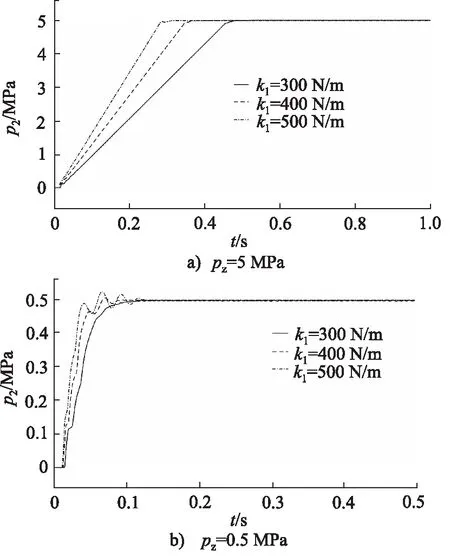
图3 不同调压弹簧刚度下减压阀阶跃响应曲线

由图3可知，电驱高压气动减压阀的响应时间随着调压弹簧刚度的增大而减小，但是当目标压力值较低时，调压弹簧刚度过大会导致出口压力值超调量较大。

2) 不同直流电机最高控制电压

设定目标压力pz为5 MPa，调压弹簧刚度k1为400 N/m，减压阀入口压力p1为40 MPa，改变直流电机最高控制电压Umax进行仿真，仿真结果如图4、图5所示。

图4 不同直流电机最高控制电压下减压阀阶跃响应曲线

由图4、图5可知，直流电机最高控制电压越大，输出转矩越大，减压阀响应速度越快；但是考虑到输出转矩过大容易超过电机的峰值转矩，造成线圈电流过大，减少电机寿命甚至是烧坏电机，直流电机最高控制电压不能太大。

图5 不同直流电机最高控制电压下输出转矩变化曲线

3) 不同活塞面积

设定目标压力pz分别为5 MPa和0.5 MPa，直流电机最高控制电压Umax为18 V，减压阀入口压力p1为40 MPa，调压弹簧刚度为400 N/m，改变减压阀活塞面积分别为设计值S的80%，100%，120%进行仿真分析，仿真结果如图6所示。

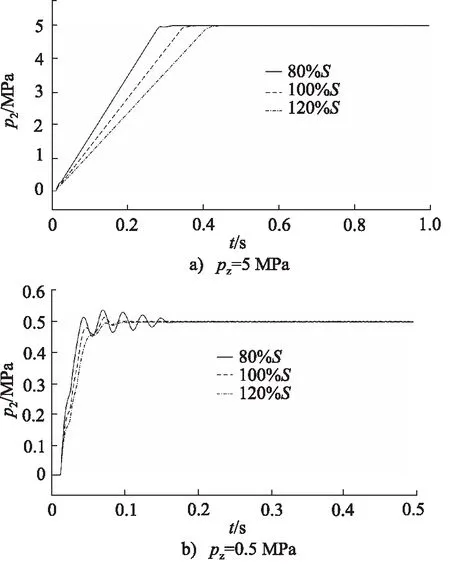
图6 不同活塞面积下减压阀阶跃响应曲线

由图6可知，减压阀活塞面积越小，阶跃响应越快，但是当目标压力值较低时超调量较大，振荡次数较多；反之，减压阀活塞面积越大，阶跃响应越慢，目标压力值较低时超调量较小。此外，减压阀活塞面积越大，阀后压力微小变化所产生作用在活塞上的气压力变化越明显，减压阀调压精度越高，但是考虑到减压阀整体尺寸的大小，减压阀活塞的面积也不能过大。

综上可知，在同时考虑减压阀调压稳定性和响应速度的情况下，选择弹簧刚度为400 N/m，直流电机最高控制电压为18 V，活塞面积为100%S作为电驱高压气动减压阀的最终设计参数。

3.3 电驱高压气动减压阀阶跃响应仿真分析

设定减压阀入口压力为40 MPa，改变减压阀目标压力分别为5, 3, 1，0.5 MPa对减压阀进行仿真分析，得到不同目标压力下减压阀阶跃响应曲线，如图7所示，在不同目标压力下，减压阀调节阀后压力达到目标压力所需时间均小于0.4 s，稳态误差在0.1%以内；目标压力值为5, 3, 1 MPa时阶跃响应曲线均没有超调和振荡，目标压力在0.5 MPa时有不超过3%的超调。

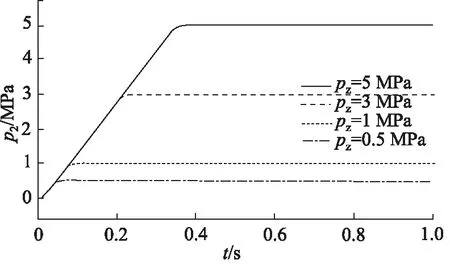
图7 不同目标压力下减压阀阶跃响应曲线

设定减压阀目标压力为5 MPa，改变减压阀入口压力分别为40，20, 10 MPa对减压阀进行仿真分析，得到不同入口压力下减压阀阶跃响应曲线，如图8所示，在不同入口压力下，减压阀阀后压力均可以达到目标压力值，且响应时间几乎相同，均小于0.4 s，满足设计要求。因此，可以认为该电驱高压气动减压阀具有在不同入口压力下调节不同阀后压力的能力。

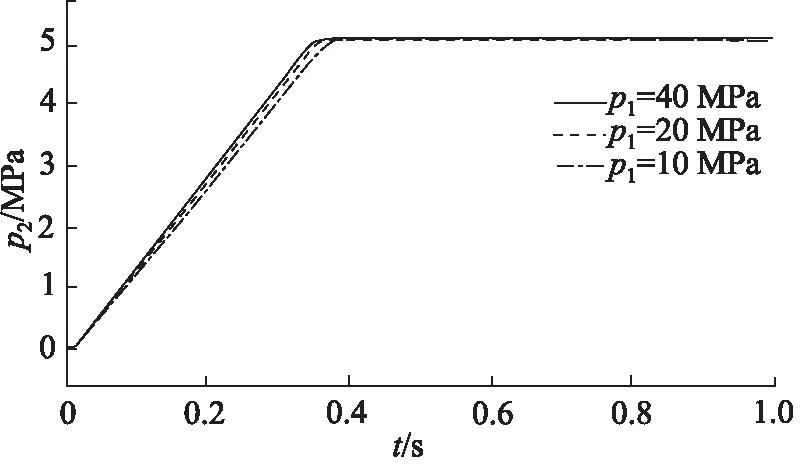
图8 不同入口压力下减压阀阶跃响应曲线

3.4 电驱高压气动减压阀正弦响应仿真分析

为了研究减压阀的动态特性，分别给定频率为1 Hz 和5 Hz的偏置为2 MPa、幅值为0.5 MPa的正弦信号作为指令信号对减压阀进行仿真分析，得到如图9所示减压阀正弦信号跟踪曲线。

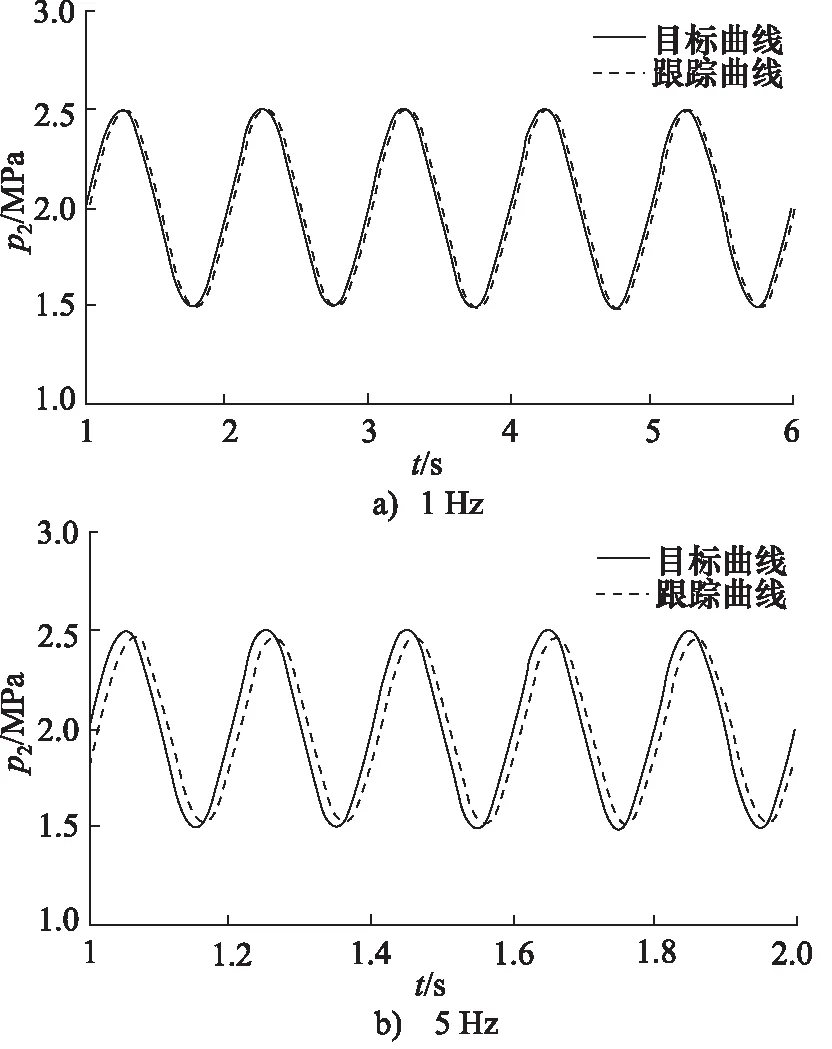
图9 减压阀正弦信号跟踪曲线

由图9可以看出，当目标曲线频率为1 Hz时，尽管跟踪过程中，减压阀的阀后压力有较小误差，但其能够较好跟踪目标位置信号，幅值基本没有衰减，相位滞后5.9°；当正弦信号的频率为5 Hz时，幅值衰减不大，幅值比为0.92，相位滞后24.84°，可以看出该电驱高压气动减压阀对变化的压力信号有较好的跟踪能力。

4 结论

(1) 本研究设计了一种电驱高压气动减压阀，采用直流电机驱动活塞直动式减压阀调压螺杆旋转下压调压弹簧，从而控制阀芯开度，最终达到作用在活塞上的气动力与调压弹簧压力相平衡，得到稳定的压力输出；

(2) 建立了电驱高压气动减压阀的数学模型，并根据数学模型对电驱高压气动减压阀进行了仿真分析，研究了相关参数对减压阀阀后压力的影响规律，并得到了较为合理的电驱高压气动减压阀设计参数；

(3) 对所设计的电驱高压气动减压阀进行了阶跃响应与正弦响应仿真分析，仿真结果表明，出口压力调节到最大出口压力5 MPa时响应时间小于0.4 s，稳态误差不超过0.1%，响应速度快，调压精度高；在5 Hz的正弦信号下，阀后压力仍能较好的保持波形，具有良好的动态性能。

本研究对电驱高压气动减压阀的结构设计和优化以及控制特性的改善具有一定的指导意义。