功能振动载荷作用下民机发动机区域液压管路动力学响应研究
权凌霄, 许孝林, 郭长虹, 史康俊, 黄自力
(1.燕山大学机械工程学院,河北秦皇岛 066004;2.南京机电液压工程研究中心,江苏南京 211153)
引言
航空发动机是为飞机提供动力的心脏,遍布发动机区域的管路为发动机和飞机输送燃油、润滑油和液压油等工作介质,是飞机重要组成部分[1]。发动机通过齿轮箱驱动液压泵工作,使液压油箱中的油液经过发动机区域液压管路系统传输到各液压用户。由于强烈振动以及黏度、压力等外部环境剧烈变化的影响,发动机区域液压管路系统经常会发生振动[2]。通过液压管路支撑组件的布置只能减弱振动,管路局部还是会发生永久性损伤,影响其疲劳寿命。并且,当该区域液压管路系统固有频率和发动机激振频率发生重叠时,会由于共振导致管路系统振动加剧,加速管路裂纹萌生。所以,为了保证发动机区域液压管路系统符合CCAR25-1435项适航条款,需要对其在功能振动载荷(民机正常飞行时振动环境)作用下进行动力学响应分析,得到管路固有频率和疲劳寿命,保证民机能正常服役。
影响航空发动机管路振动的因素较多,主要包括液压管路中的油压脉动、发动机转动引起的系统激振、噪声振动以及流量脉动和气体引起的激振等。目前针对管路振动的研究取得较多成果。林君哲等[3]采用牛顿法建立了航空发动机液压管路在基础激励下的非线性流固耦合振动数学模型,并通过数值仿真分析了航空发动机液压管路的流体压力、流速、轴向力等参数对振动特性的影响;杨同光等[4]通过采用磁力研磨方法提高不锈钢弯管内表面质量并进行试验,验证了提高内表面质量对弯管振动的影响比其他因素都小;郭长虹等[5]通过传递矩阵法创建了国产大飞机C919的一段多弯曲液压管路的完整传递矩阵动力学模型,并进一步分析和试验验证了该管路在正常飞行振动载荷和功能冲击载荷下的流固耦合振动;寸文渊等[6]基于模态分析研究了某型飞机液压管路的故障危险模态并对管路进行了改进;MAMAGHANI等[7]研究了非线性能量对输流管路在激励下的减振影响;AKIRA M等[8]针对管路的振动应力测量问题,提出了一种多点输出的非接触测量方法;KIM B L等[9]通过开发一种改进的振动传递路径分析方法,更精确的分析和估计受到多振源、激励和多干扰的复杂系统的主要振动源的作用力,并将其应用于估算空调机组的振动力。
本研究针对ARJ21-700民机发动机区域某根回油液压管路进行功能振动载荷下动力学分析,研究功能振动载荷对发动机区域液压管路的安全和寿命影响。首先,通过传递矩阵法建立研究对象的动力学数学模型;其次,利用ABAQUS软件对管路进行功能振动载荷下动力学分析并求解其裂纹萌生寿命;最终,和试验结果进行对比,验证分析功能振动载荷对于发动机区域液压管路的影响。
1 管路动力学模型
图1所示为ARJ21-700民机发动机区域某根回油液压管路,主要由直管及弯管部分组成,故需先计算每段管路的传递矩阵,从而最终建立管路整体的传递矩阵[5]:

图1 ARJ21-700民机发动机区域管路模型
N1(s)M1(L1,s)
(1)
式中,Ni(s)为点传递矩阵,当管路截面和材料不变时为单位阵。模型中管段1,5,9轴线分别异面,在管段4,6进行坐标旋转,对其进行坐标变换,其坐标变换关系为:
(2)
式中,R5(s),R3(s)为坐标旋转矩阵,坐标旋转矩阵在三维弯管模型上最早由DAVIDSON等[10]应用,其式为:
R=

(3)
式中,φ为管路坐标旋转角度。
由此可得图1所示发动机区域管路的全局传递矩阵:
Mall(z,s)=M9(L9,s)…M6(L6,s)R5(s)M5(L5,s)×
M4(L4,s)R3(s)M3(L3,s)…M1(L1,s)
(4)
2 ABAQUS有限元分析
2.1 管路模型抽壳及基础设置
在分析过程中为了减少计算量以及提高计算精度,通常对管路模型进行抽壳,在Part(部件)模式下,分别对管路模型提取壳体,抽壳示例如图2所示。

图2 管路抽壳示例
此外,在分析时对模型进行基础设置,设置各部分属性,管路材料属性如表1所示,对接头、卡箍和管路之间设置约束,分别在接头和管路间设置Tie约束、卡箍和管路间设置MPC约束,并设置边界条件及压力载荷等。
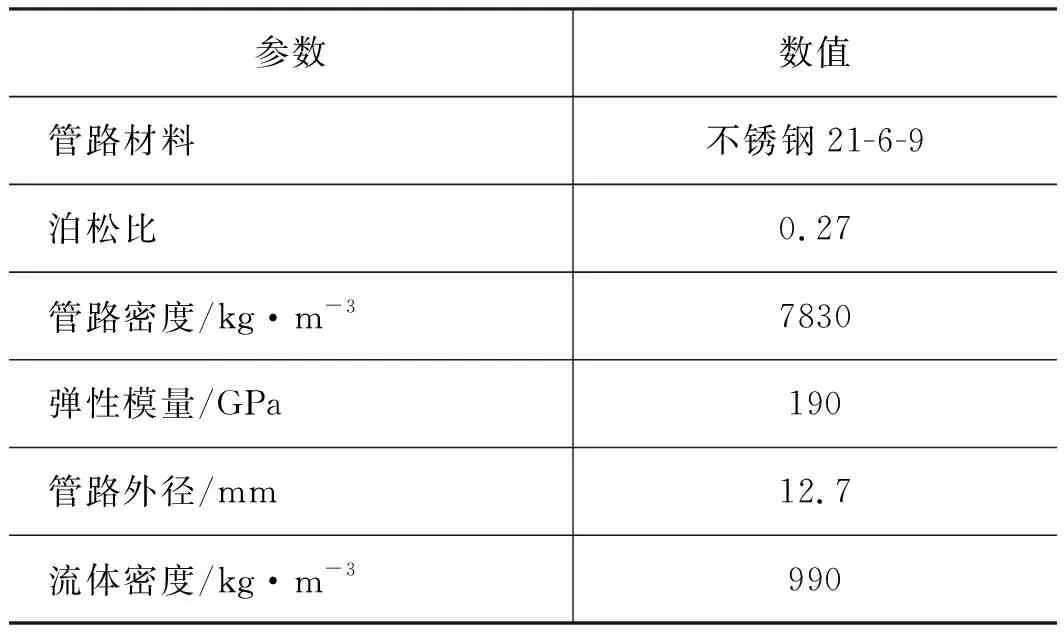
表1 管路材料牌号及性能参数
2.2 模态及功能振动分析设置
根据《CCAR-25运输类飞机适航标准》435项适航条款以及《RTCA-DO-160G 机载设备的环境条件和试验程序》文件要求,发动机区域液压管路系统除进行模态分析外,还需针对功能振动载荷下的发动机区域管路进行分析;根据如图3所示的飞机机载设备机械环境技术大纲(振动冲击加速度)振动功能试验量值,设置如表2所示的功能振动载荷,考核设备在正常飞行振动环境条件下能否满足功能要求。
3 模态分析及振动响应结果
3.1 模态分析结果
对管路进行两端固支并加压10 MPa进行模态分析,得到管路的各阶固有频率,如表3所示,其位移云图如图4所示。
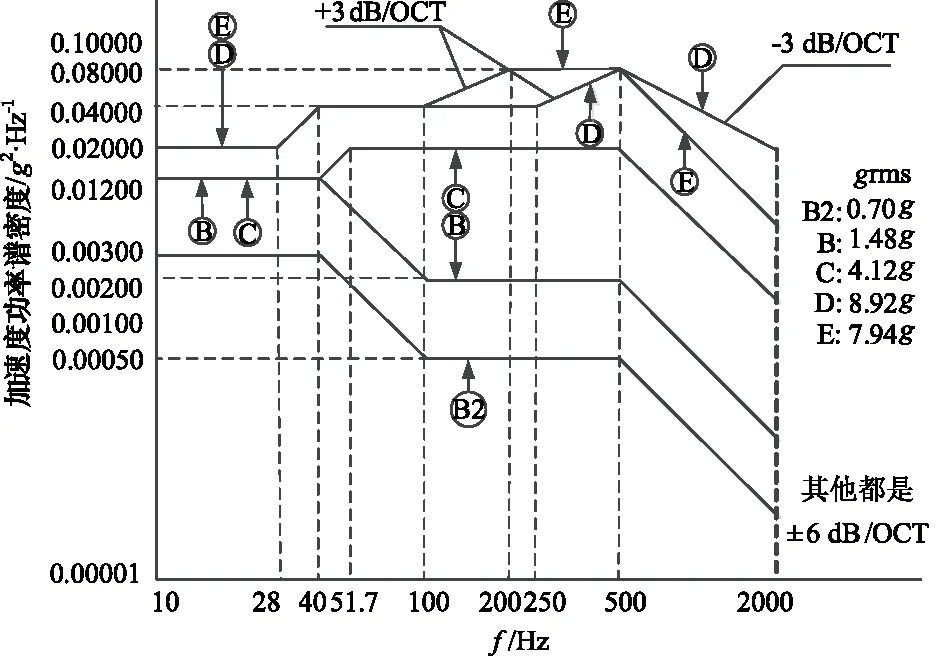
图3 功能振动试验量值(随机)
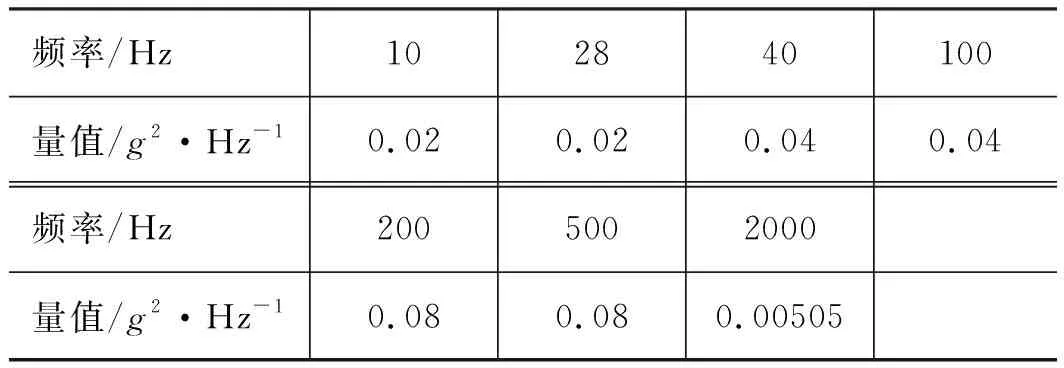
表2 随机功能振动试验曲线转折点对应量值(E区)

表3 两端固支下管路各阶固有频率

图4 管路各阶固有频率位移云图
3.2 功能振动响应分析
数值分析得到在压力为10 MPa,随机振动载荷激励下,管路在X,Y,Z方向上振动频率为2000 Hz时的应力均方根RMS,应力均方根值最大处,即为管路最危险的位置,输出此位置的应力响应功率谱曲线图,如图5所示。
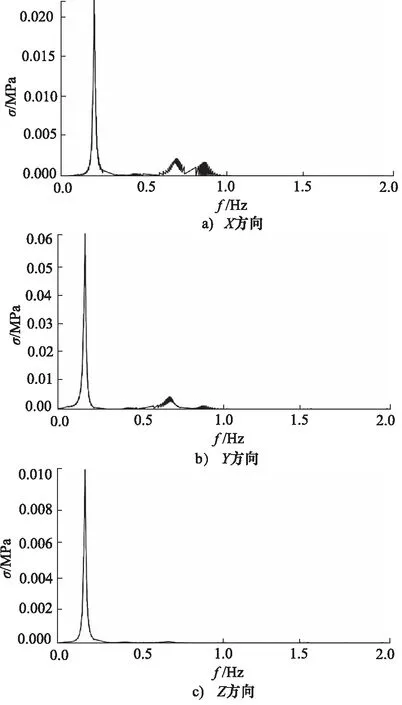
图5 各方向应力响应功率谱曲线图
1) 计算功能随机振动疲劳寿命
工程上常用谱宽参数来描述应力过程的不规则性,当谱宽系数低于0.3时,随机过程归于窄带过程;当谱宽系数达到1时为理想宽带过程。宽带随机振动疲劳寿命计算公式:

(5)
修正因子:
λ=0.926-0.033m+(0.074+0.033m)×
(1-∂)1.587m-2.3323
(6)
随机振动零穿越期望值:
(7)
不规则参数:
(8)
标准方差:
(9)
式中,G(f)为应力功率谱密度(PSD)函数;m,c为材料系数,由S-N曲线拟合为幂函数形式方程SmN=c获取。
2) 计算材料系数m和c
由《SAE AMS 5561G-2007》温度-性能曲线(9.0Mn-20Cr-6.5Ni-0.28N)中不锈钢的S-N曲线,求m,c常数。
S-N曲线的一般函数表达式通常有3种,分别为幂函数形式、指数函数形式及三参式。结合工程实际,为方便计算随机振动疲劳寿命,将S-N曲线拟合为幂函数形式SmN=c,幂函数式中S为应力幅值,N为应力幅值为S时的循环次数。
依据应力循环比k,应力幅值S及最大应力Smax之间的函数关系,结合材料S-N曲线,计算出应力幅值S所相对应的应力循环次数。
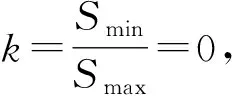
(10)
通过上式将S-N曲线中纵坐标处最大应力转换为应力幅值,并取坐标点由SmN=c计算得到材料系数m和c,k=0时,m=5.816,c=8.285×1017;在k=-1时,m=5.816,c=3.506×1020。
3) 依据Miner线性损伤累积理论
利用数学软件MATLAB编写振动疲劳寿命计算程序,求得疲劳寿命如表4所示。

表4 功能振动载荷下管路寿命 s
4 试验验证
由于缺少发动机区域管路,故本次试验采用验证性试验,用以验证数学模型和仿真方法的正确性。试验采用如图6及图7所示前机身液压管路作为试验研究对象,试验时,利用软管将管路连接至试验系统中。

图7 试验管路安装图
4.1 模态试验
以正弦扫频信号作为管路的振动激励,测试管路的振动特性,为管路模态分析提供验证依据。由于激振器激振方向为Y方向,故在此分析Y方向的振动频域响应。
试验得到管路在不工作状态下,管路外壁各点加速度响应曲线如图8所示。数值分析可以得到管路的一阶固有频率,如图9所示,将其与试验结果对比,如表5所示。对比分析可以看出,试验和数值分析结果误差较小,分析方法正确,且当振动频率接近管路的各阶固有频率时,管路表面加速度明显增大,产生共振现象。

表5 模态试验管路一阶固有频率
4.2 功能振动试验
以功能振动载荷下的加速度功率谱密度作为管路的振动激励信号,测试管路在功能振动载荷下的振动响应,其功能振动功率谱密度量值如表2所示,试验结果如图10所示,为管路功能振动分析提供了验证依据。
对试验管路进行数值分析,得到在压力为10 MPa,随机振动载荷激励下,管路外壁各点加速度曲线,如图11所示,由于激振器激振方向为Y方向,故在此分析Y方向的振动频域响应。
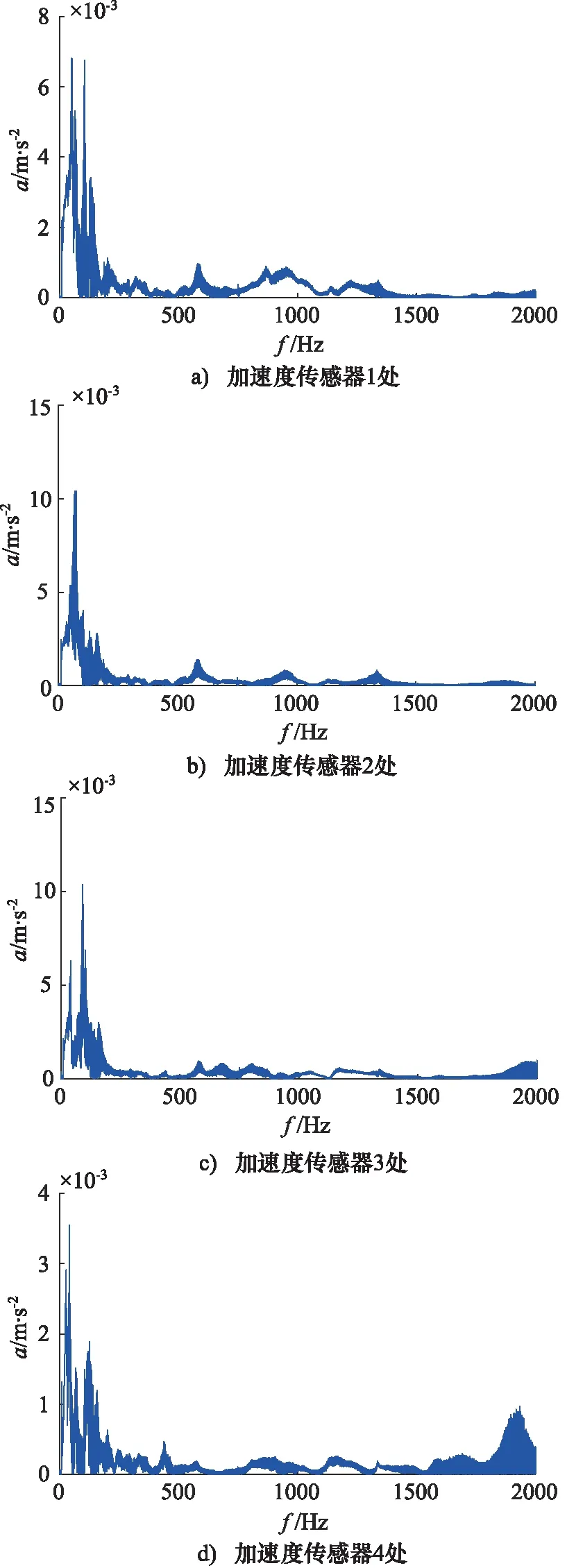
图8 管路外壁各点加速度响应曲线(Y方向)
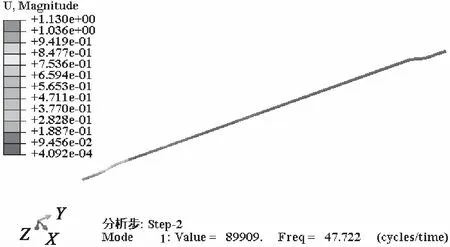
图9 数值分析管路一阶固有频率位移云图

图10 功能振动载荷下管路外壁各点加速度曲线(Y方向)

图11 功能振动频域响应数值分析结果(Y方向)
对比图10试验结果和图11数值分析结果中最大加速度,如表6所示,可见误差在10%以内,数值分析方法基本正确。
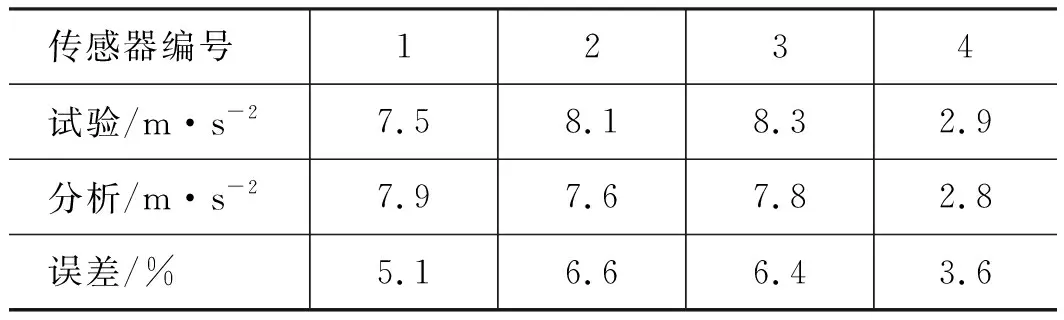
表6 功能振动试验加速度传感器1~4处的最大加速度
5 结论
通过以上研究,针对ARJ21-700民机发动机区域回油液压管路受功能振动载荷的影响,通过理论分析、数值仿真和试验验证可以得到以下结论:
(1) 通过模态分析和试验可以确定管路固有频率,且对比分析和试验误差小于10%,可以验证分析正确性;
(2) 在功能振动分析时,当激振频率接近管路各阶固有频率时,管路表面加速度明显提高,分析和试验共同证明在此情况下管路会出现共振现象,验证了分析正确性;
(3) 基于线性损伤累积理论得出管路疲劳寿命,可以看出飞机发动机区域液压管路寿命远高于60000 h的飞行寿命标准,管路寿命可以视作无限,满足飞机飞行安全要求。

