考虑便乘的地铁乘务任务配对的约束优化模型研究

马 亮，徐晓英

(1. 西南交通大学 信息科学与技术学院，四川 成都 610031；2. 中国铁路西安局集团有限公司，陕西 西安 710608)

地铁车辆基地(包括车辆段和停车场)主要作业任务为检修、行车和乘务，行车依据检修需求和车辆状态为运行车次分配车辆，乘务管理为行车提供司乘保障。乘务管理的核心是依据乘务制度编制乘务排班计划，实现乘务任务、司机出/退勤、司机轮休、司机用餐和司机工作量的管理，保障正线行车效率和乘务人员身心健康，达到减员增效的目的。

乘务排班计划主要包括：乘务任务配对(Crew Scheduling)和乘务任务指派(Crew Rostering)两个问题。其中，乘务任务配对是指依据乘务作业限制，将给定的列车运行计划配对成若干乘务任务；乘务任务指派是指依据乘务班组和轮班制度将乘务任务配对结果指派给具体的司乘人员，形成司乘人员一天的值乘计划。一般情况下，司乘人员驾驶列车出勤或者值乘，若司乘人员不在出勤点或者退勤点，就需要像乘客一样便乘其他列车至出勤点或者退勤点。因此，乘务任务可以分为值乘任务(Crew Tasks)和便乘任务(Passenger Tasks)。便乘是指多组司乘人员同时值乘一个列车，其中1组司乘人员担任司机，其他组司乘人员以乘客身份便乘前往目的地出勤或者退勤，即部分司乘人员只能在非出勤点开始乘务任务或者在非退勤点结束乘务任务。

国外针对铁路司乘任务优化问题：文献[1]考虑了司乘人员可以乘坐其他交通工具便乘出勤和对原有乘务任务修改最少，建立了荷兰铁路司乘人员重新调度的集合覆盖(Set Covering, SC)模型，但是重新调度的计算时间较长；文献[2]研究了铁路货物夜间运输的乘务任务公平调度问题，以乘务任务调度成本最小、不受欢迎的乘务任务最少和不受欢迎乘务任务分配均衡为目标，建立了欧洲铁路运输公司乘务调度的SC模型，并设计了最短路径和线性规划松弛的混合算法；文献[3]重点考虑了任务调度和司乘人员薪酬的均衡性，建立了智利工矿企业工艺铁路的乘务任务调度的0-1整数规划模型，但是改进的局部启发式搜索算法求解耗时达几个小时。由于国外法规制度和铁路值乘制度与国内不同，因此需要研究符合我国国情的乘务任务配对优化问题。

针对我国铁路乘务排班计划优化问题：文献[4]建立了台湾地区铁路客运乘务排班计划的综合0-1优化模型，并使用深度优先回溯搜索算法(DFS)求解，算例表明综合模型比分解模型的解更优；文献[5]以总交路时间最小和各乘务交路间均衡最大为目标，建立乘务交路优化的多旅行商模型，算例验证表明改进蚁群算法比遗传算法求解效果好；文献[6] 建立了客运专线乘务交路计划的SC模型，但是分支定价算法求得初始解的时间较长，算法的可信度不高；文献[7]以乘务人员效率最高为目标，建立了乘务交路计划的SC模型，但是模型中未考虑便乘情况、实际的乘务制度、劳动规章等关键因素。

相对于国铁，地铁具有乘务任务段相对确定、行车密度大、交路相对简单、有多个乘务轮换点等特点。目前，现场绝大多数司乘派班调度员借助办公软件人工编制司乘排班计划，司乘班组的工作效率得不到保证，需要研究地铁乘务排班优化问题。文献[8-10]以总费用最少为目标建立双层整数规划模型，并分别使用最短路、最小费用最大流、Hungarian、禁忌搜索、Dijkstra和离散粒子群等算法求解；文献[11]探讨了乘务排班和值乘方式，比较得出轮乘制比包乘制更节省费用；文献[12-13]建立乘务任务配对的SC和集合分解(Set Partition, SP)模型，并借鉴列生成思想设计混合算法求解；文献[14]建立乘务任务分配的0-1整数规划模型，设计了列生成和跟随分支策略的混合算法，但是应该考虑更长期乘务任务的均衡性；文献[15]针对启发式算法或者列生成算法求解复杂、难于实际应用等问题，以列生成算法为框架，将整个优化问题分解为SP主规划模型和加权网络最短路径的子规划模型两部分，但是在实际应用时成本函数中的权值较难确定。

现有研究主要是建立乘务排班计划的0-1规划模型，再使用解析算法和启发式算法求解，取得了大量的理论成果，但是与投入实际应用之间存有一定的差距。关键问题是所建模型是结构化的数学表达式，难于使用程序语言直接表示；而且针对不同的算例，算法性能的波动较大。同时，部分模型存在不深入和值得商榷的地方，譬如：乘务任务与乘务任务段之间的关系定量描述不精确、各约束没有分情况讨论等。本文使用约束程序(Constraint Programming, CP)[16-17]理论研究便乘情况下的乘务任务配对问题，建立约束优化(Constraint Optimization, CO)[17]模型，并依据模型特点使用弧边界相容的约束传播(Constraint Propagation, CPr)[17]算法化简模型，最后使用CPr和启发式回溯的混合算法求解模型。

1 地铁乘务任务配对问题

乘务任务配对指将给定的列车运行计划配对成若干乘务任务，每个乘务任务由1个乘务班组1天完成，因此，列车运行图是乘务任务配对的基础。列车运行图中纵轴表示所有停靠车站，这些车站按照用途可以分为两类：一类是普通乘客换乘点；另一类是乘务分割点。其中乘务分割点是乘务员进行出/退勤、轮换休息和用餐的站点。移除列车运行图中的乘客换乘点得到只保留乘务分割点的乘务运行线集合为

G={Gi,1≤i≤NG}

式中：Gi(1≤i≤NG)为第i条乘务运行线集合；NG为总的运行线数量。

将每一条乘务运行线Gi上相邻乘务分割点之间的运行任务片段称为乘务任务段，则第i条乘务运行线Gi的第l个乘务任务段为

乘务任务段划分示意图见图1。

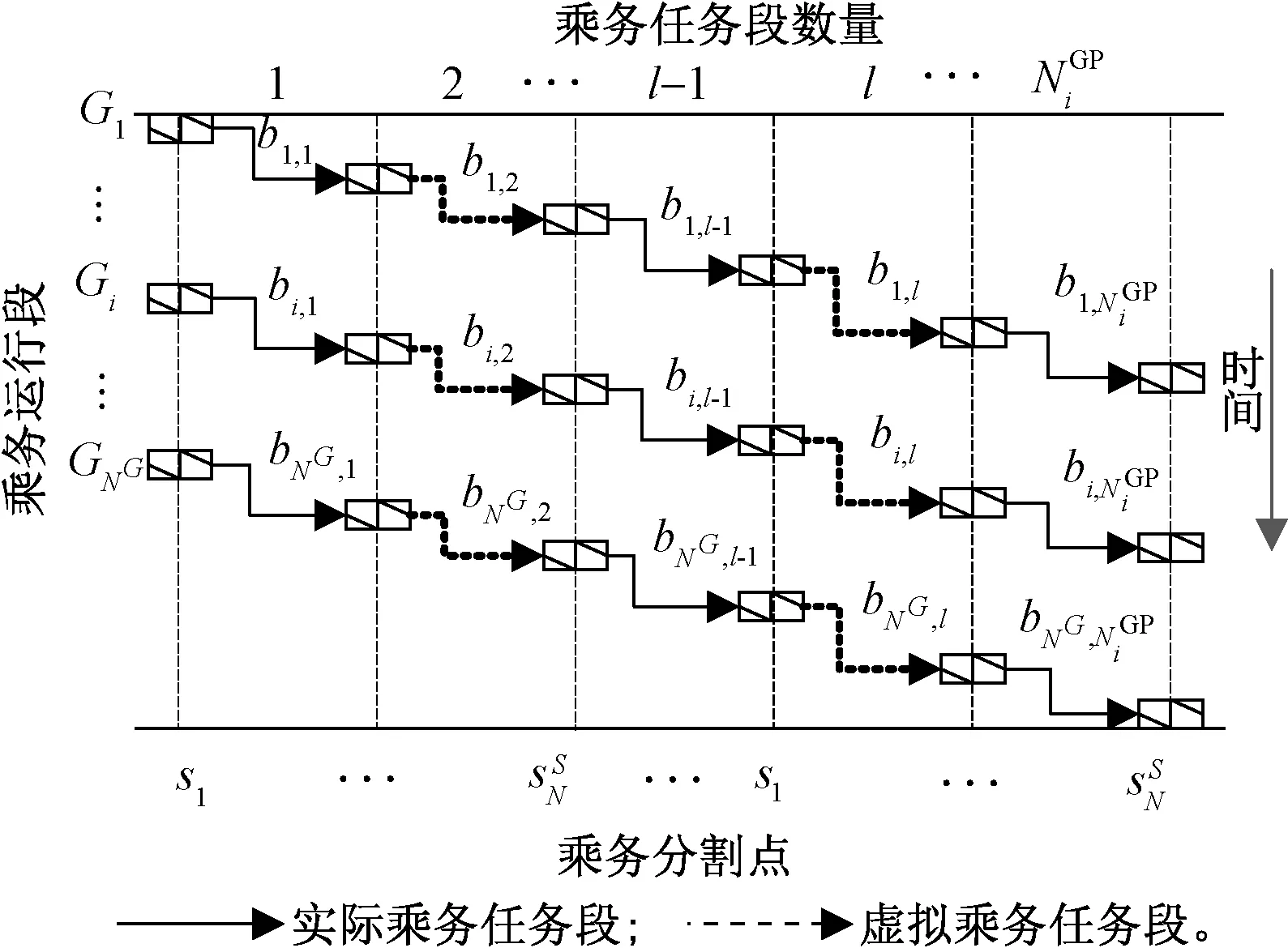
图1 运行线的乘务任务段划分示意图

为了论述乘务任务配对问题，定义变量见表1.

表1 乘务任务配对问题变量及说明

一个乘务任务是指司乘人员从出勤点开始，值乘若干乘务任务段并最终从退勤点结束的全过程[5]，由若干乘务任务段按照一定的乘务规则链接而成。因此，乘务任务段是乘务任务配对的基本单元，其数量与每日列车运行次数、乘务分割点的分布密切相关，并直接决定了乘务任务配对问题的复杂度。乘务任务段之间的树形链接关系见图2。

图2 乘务任务段链接关系的树形结构示意图

2 地铁乘务任务配对的约束优化模型

CO模型记为四元组(X,D,C,F)，其中：X为变量集合；D为变量论域集合；C为约束集合；F为目标函数集合[17]。令某一变量x∈X取值表示为x←v∈D(x)，则CO求得最优解S={(x←v)|∀x∈X,v∈D(x)}是指对于任意约束∀c∈C满足相容性检查c(S)=1，同时使得任意目标函数∀f∈F达到最优。CO的约束是由变量或者变量表达式之间通过逻辑谓词(与“∧”、或“∨”、非“！”、蕴含“=>”等)联接形成的关系[17]。乘务任务配对受到地点、时间、工作强度等限制，而且各约束之间存在较强的逻辑关系，使用CO直接建立考虑便乘的乘务任务配对优化模型(Constrained Optimization Model for Crew Pairing, COCP)。

2.1 常量定义

表2 常量变量及说明

2.2 变量定义

每一个乘务任务段可以视为最小的乘务任务，理论上最多的乘务任务数量等于NB，令以bm为开始任务区段的乘务任务Bm为变量，则定义变量见表3。

表3 任务区段的乘务任务Bm为变量及说明

依据上述定义，乘务任务的结构见图3。

图3 乘务任务结构示意图

2.3 目标函数

为了降低地铁运营成本和提高乘务人员的工作效率，乘务任务配对优化的主要目标是在允许便乘的情况下乘务任务数量最少，表示为

(1)

2.4 约束条件

乘务任务配对需要满足乘务人员总的工作量、乘务人员连续工作量、乘务任务的班次划分、出/退勤地点、轮休时间和地点、用餐时间和地点、乘务任务段完整性等限制。

(2)

(2)1个乘务任务内相邻的乘务任务段之间，前1个乘务任务段的到达地点是后1个乘务任务段的出发地点，即乘务任务内的乘务任务段之间需要满足链接关系

(3)

(3)如果某一个乘务任务的开始车站不是出勤点或者结束车站不是退勤点，那么此乘务任务段为便乘的乘务任务段

c3:∀m:(om=1∧wm=1)

(4)

(4)在最终形成的乘务任务方案应该包括所有的乘务任务段，而且1个乘务任务段只属于1个乘务任务。则乘务任务段全覆盖和唯一性约束为

(5)

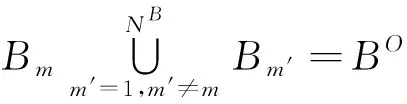
(5)为了保证乘务人员之间的工作量均衡，每一个乘务任务需要满足所属班次总的工作量约束为

(6)

(6)所形成的乘务任务Bm中所有的乘务任务段要么没有特殊的需求，要么满足退勤、轮休、用餐中的1个需求，则乘务任务段特殊需求唯一性约束为

c6:∀m,∀n:(om=1)⟹(dm,n=rm,n+hm,n+em,n)

(7)

(7)为了保证各司乘人员工作量均衡和避免疲劳驾驶，乘务任务内总的工作时间不能超过上限，否则，需要退勤，则总的工作量约束为

(8)

式(8)表示当乘务任务Bm满足其他约束的论域D(Bm)不为空时，但是其中任意乘务任务段加入到Bm中均会超过总的工作时间的上限，则需要退勤。

(8)为了保证司乘人员的身心健康，司乘人员连续工作时间不能超过持续工作时间上限，如果超过，则需要轮换休息，则连续工作量约束为

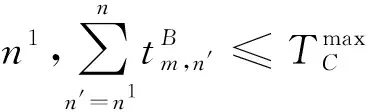
(9)一般情况下乘务任务分为早、白、夜3班，通过乘务任务的开始和结束时间来区分乘务任务所属班次，则乘务任务班次划分约束为

c9:∀m,∃u∈ST:(om=1∧um=u)

(11)

(10)早班中的非便乘出勤的乘务任务直接从车辆基地驾驶出勤

(12)

(11)晚班中的不是便乘退勤的乘务任务直接驾驶到车辆基地退勤：

(13)

(12)为了保证司乘人员的身心健康，乘务人员连续驾驶一段时间之后需要在轮换点休息，则乘务任务的轮换休息持续时间和地点约束为

(14)

(13)乘务人员连续驾驶一段时间之后需要在规定地点和时间范围内用餐，而且需要保证用餐时间，则乘务任务的用餐持续时间和地点约束包括是否用餐约束和用餐时间、地点约束为

(15)

COCP模型为单目标的约束优化模型，每一个乘务任务的确定问题为大规模的NP-Hard问题，首先通过约束传播算法剔除解空间中不可能成为解的那部分变量取值，缩小解空间，减少无效搜索。但是约束传播算法缺乏完备性，同时基本回溯算法(Backtracking Algorithms, BT)未使用已实例化变量进行相容性检查避免未来冲突，求解时间较长，因此，设计了约束传播和启发式回溯(Heuristic BT, HBT)的混合搜索算法(CPr-HBT)快速求解模型。

3 乘务任务配对的混合搜索算法

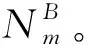
(16)

混合搜索算法(CPr-HBT)步骤如下：

Step1如果未达到总的求解时间或者迭代次数，转Step2，否则，返回使得f最小的解B={Bm}。

Step4初始约束传播约减D(Bm)。在使用启发式回溯算法求解乘务任务Bm前，使用约束传播算法对乘务任务Bm的论域D(Bm)进行约减，转Step5。

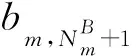
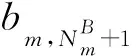
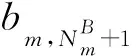
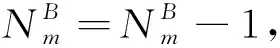
4 算例分析

4.1 算例求解

某地铁线路的站点设置见图4，共有北郊、军区和太平3个乘务分割点。其中北郊为车辆段，北郊和军区为出/退勤点、军区和太平为乘务轮换休息点、军区为用餐点。

某日此地铁线路有101～120共20个运行车次，其中101～118车次之间的间隔为10 min、单向运行次数都为18、在同一单向运行中相同乘务分割点轮换休息时间相同，119和120车次之间的间隔为5 min、单向运行次数都为4、在同一单向运行中相同乘务分割点轮换休息时间相同。不同车次相同运行区间的运行时间相同，其中北郊和军区之间双向运行时间均为10 min，军区和太平之间双向运行时间均为45 min，则依据运行图和乘务分割点划分得到101和119车次的乘务任务段见表3，表格中b1,l(1≤l≤20)为101车次的乘务任务段，b19,l(1≤l≤6)为119车次的乘务任务段，102～118车次的乘务任务段划分类似于101车次的乘务任务段划分，120车次的乘务任务段划分类似于119车次的乘务任务段划分。模型中其他参数见表4。

图4 某地铁线路的站点设置示意图

表3 某地铁线路某日乘务任务段

表4 某地铁线路乘务计划参数表

本算例的乘务任务段总数为372，变量有1 442个，约束的数量级为百万，在Inter Core i3-2 310 M 2.1 GHz & DRAM 2 G & Windows XP &.NET Framework 4.5环境下的PC机上运行本模型及算法，根据现场需求设置算法总的求解时间上限为200 s或者总的迭代次数上限为20 000次。CPr-HBT算法的求解过程见图5，乘务任务配对结果见表5、图6。从图5中可知求得较优解至少需要迭代5 600次，总的花费时间为56.35 s，产生了56个乘务任务，在这些乘务任务中需要进行31次便乘，乘务员之间工作时间最多相差了310 min。

图5 CPr-HBT混合算法的求解过程

图6中早班、白班和夜班各有两种情况。早01～早18的乘务任务为∀i=1…18:{bi,l|l=1…9}，早19～早20的乘务任务为∀i=19…20:{bi,l|l=1…6}；白01～白09的乘务任务为∀i=1…9:{bi,l|l=10…16}，白10～白18的乘务任务为∀i=10…18:{bi,l|l=10…15}；夜01～夜09的乘务任务为∀i=10…18:{bi,l|l=16…20}，夜10～夜18的乘务任务为∀i=1…9:{bi,l|l=17…20}。

从图5中的算法求解过程可以看出：目标函数值是单调递增或者递减的，较少出现震荡，说明通过约束传播技术保证了最优解的求解效率和概率。通过图6可得：乘务任务覆盖了表1中所有的乘务任务段，所有的乘务任务满足所有约束条件，而且满足现场的对计划编制的时效性需求。

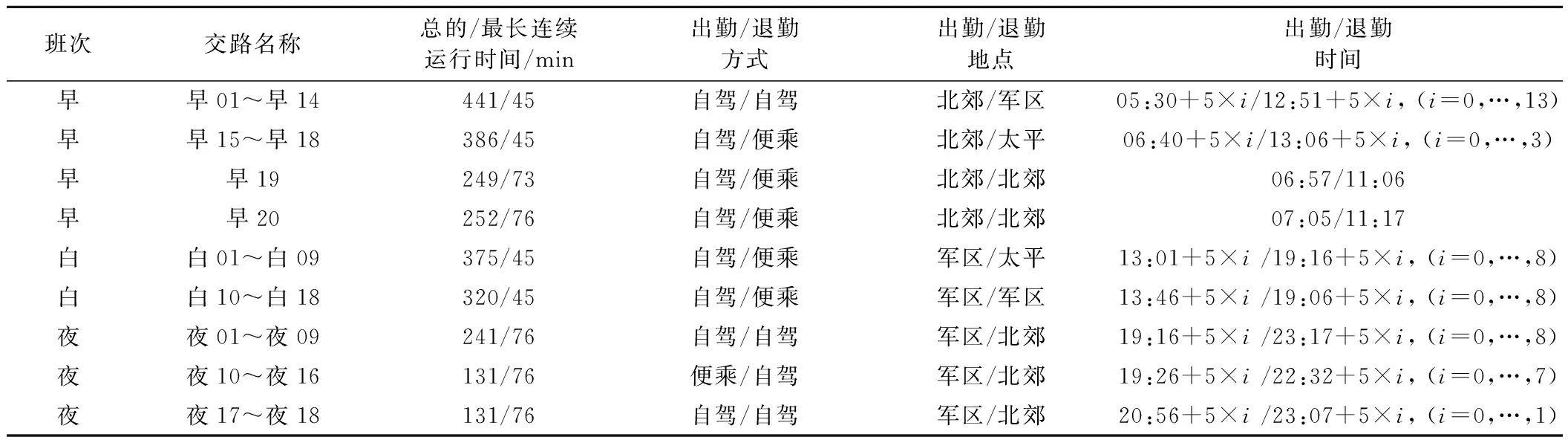
表5 乘务任务配对结果

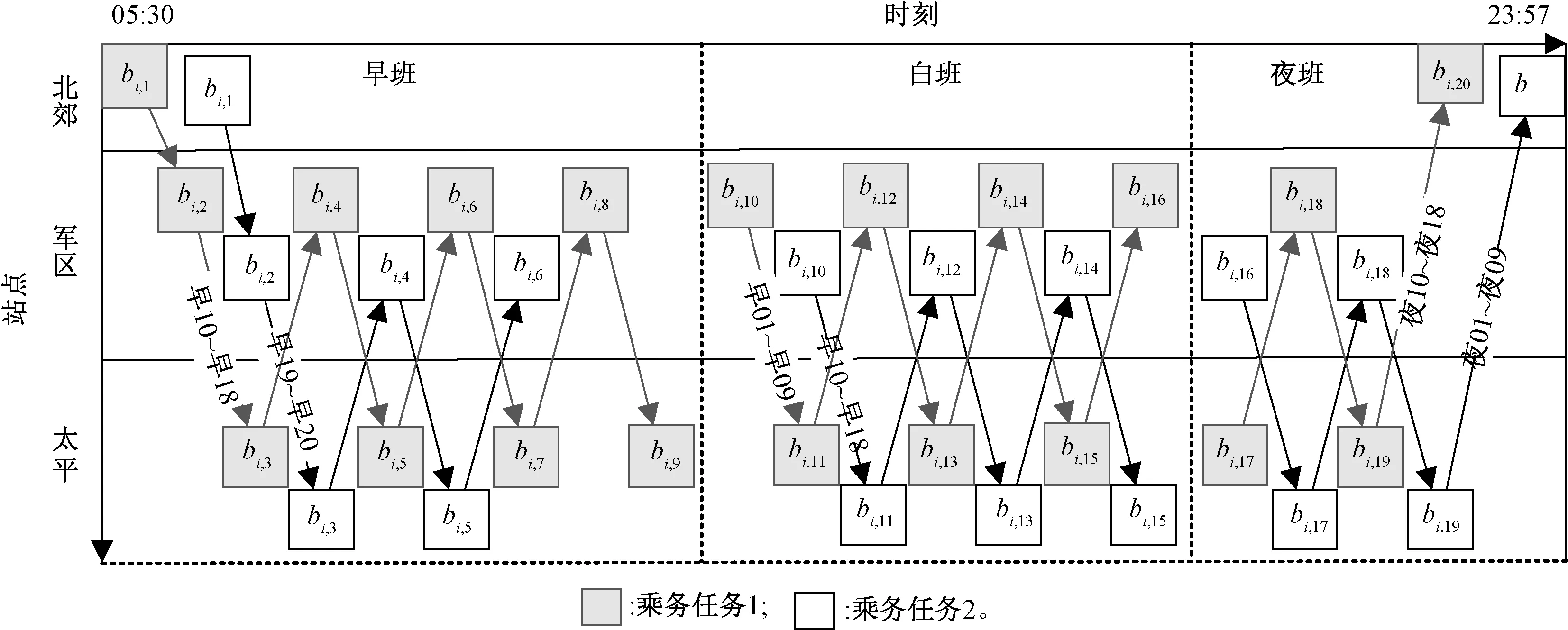
图6 乘务任务配对结果示意图

4.2 算法比较

为了验证本算法的求解效率，在不改变其他参数的情况下，使用文献[4]中不带约束传播的深度优先回溯算法(DFS)求解本模型，求解过程见图7。

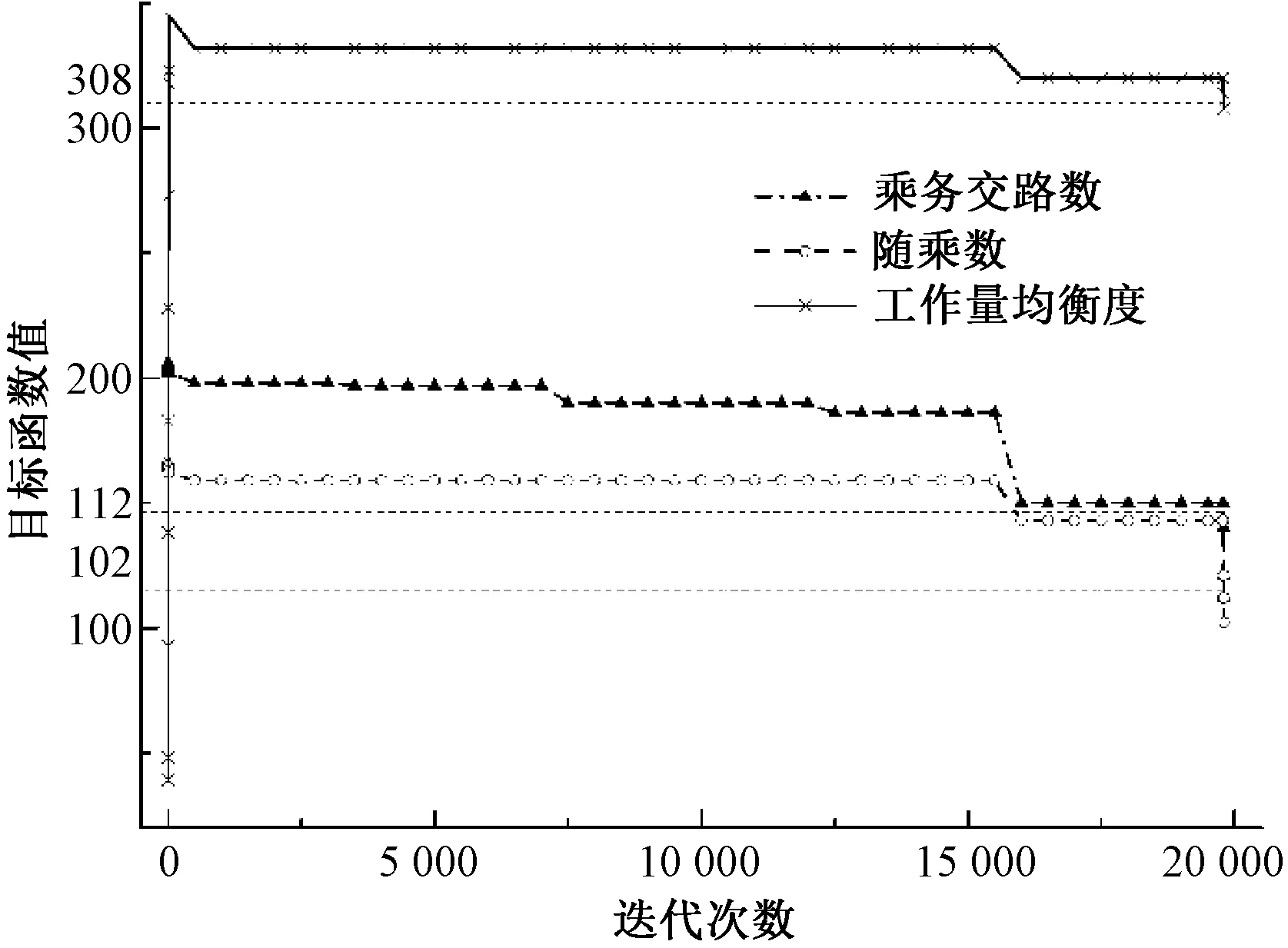
图7 使用DFS算法目标函数的求解过程

DFS达到迭代上限20 000次时，形成的乘务任务数为112个乘务任务，有102次便乘，乘务员之间总的工作时间相差了308 min。因此，不带约束传播的改进回溯算法的求解效率和求解质量都比本文算法要低，验证了本混合算法的高效性。

5 结论

本文综合考虑了乘务人员的工作效率、工作量的均衡性和乘务员便乘等因素，建立了考虑便乘的乘务任务配对的约束优化模型。之后设计了约束传播与启发式回溯的混合算法求解了模型；最后通过现场实际算例验证结果表明：与现场和其他算法相比，本论文的模型和算法优势明显。本论文提出的使用约束程序方法对于考虑便乘的地铁乘务任务配对优化问题是可行的，模型符合现场实际业务需求，保证了排班计划的适用性；本混合算法求解效率和稳定性较高，满足现场对排班计划编制的实时性要求。本论文提出的模型和算法已经成功应用于地铁车辆基地综合自动化系统中，结合乘务任务指派优化方法，共同辅助司乘派班调度工作，降低了派班调度员的工作强度，提高了作业效率。