考虑残余强度修正的混凝土冻融损伤层及轴心受压模型研究

关 虓，牛荻涛，肖前慧

(1.西安科技大学 建筑与土木工程学院，陕西 西安 710055; 2.西安建筑科技大学 土木工程学院，陕西 西安 710055)

对寒冷地区的混凝土结构而言，冻融破坏是引起其性能劣化的主要原因之一，严重影响混凝土建筑物的安全使用及长期寿命[1-5]。因此，近年来不少学者致力于各类混凝土抗冻性及冻融损伤评价方法的研究，并取得了许多有益成果[6-11]，但仍存在以下几点问题：①对于实际工程结构冻融损伤度的评估，传统的抗冻性评价指标——强度、质量、动弹性模量适用性不强；②冻融损伤层不仅能反映冻融损伤演化特点，且便于工程检测，但目前以冻融损伤层为冻融损伤度评价指标的研究还不多，尤其是现阶段所采用的超声波无损检测方法测得的结果准确性还不高；③现阶段的研究成果大都采用理想化的水冻水融加速试验方法，这与大气环境中混凝土结构所遭受的气冻气融作用存在较大差别[12]；④对于已遭受冻融破坏的既有结构，如何根据易于检测的损伤评价指标(如损伤层厚度)建立相应的损伤本构模型，进行结构使用寿命的科学预测，是目前亟待解决的工程问题。

鉴于此，本文开展了混凝土气冻气融试验及冻融后的混凝土轴心受压试验，系统研究冻融后混凝土损伤层的演化规律，并以冻融损伤厚度作为混凝土冻融循环损伤的评价指标，考虑损伤层内的残余强度，引入修正系数，提高损伤层评价损伤度的准确性；同时，根据损伤力学相关理论，建立基于冻融损伤层厚度的混凝土轴心受压本构模型。

1 试验概况

1.1 混凝土配合比及试件分组

本次试验所用水泥为P·O42.5普通硅酸盐水泥；粉煤灰为Ⅱ级粉煤灰；聚羧酸系减水剂，减水率20%～25%；粗集料为5～31.5 mm连续级配天然碎石；细集料为渭河细砂，细度模数2.0。混凝土试块配合比见表1。试验共制作了42个尺寸为100 mm×100 mm× 100 mm的立方体试件及 41个尺寸为100 mm× 100 mm×300 mm的棱柱体试件，用于开展冻融混凝土轴心受压试验及损伤层厚度的测试，其中水胶比0.55组14个棱柱体，15个立方体；水胶比0.45组12个棱柱体，12个立方体；水胶比0.35组15个棱柱体，15个立方体，所有试件冻融循环目标次数均为300次。

表1 混凝土配合比及强度

1.2 试验装置

冻融试验采用气候环境模拟试验箱，其通过工作室内环境温度的改变模拟大气环境中的冻融机制(而非水冻水融中冷冻液改变温度)；冻融损伤层厚度采用北京康科瑞仪器有限公司生产的NM-4B非金属超声波探测仪；轴心受压试验采用天水红山试验机有限公司生产的500 t微机控制电液伺服压力试验机、YHD-10型号位移传感器及TDS-602数据采集仪，最大加载速度为50 mm/min，最小加载速度为0.01 mm/min。

1.3 试验方法

依据文献[13]中慢冻法的相关规定及课题组对陕北寒冷地区大气环境中正负气温变化监测数据确定冻融试验升降温机制为：正温设定为15 ℃，负温为-19 ℃，由设定正温值降至设定负温值用时2 h，并在达到负温设定值后恒温2 h，整个冻结过程持续4 h；再由设定负温升至设定正温用时0.5 h，并在设定正温值恒温1.5 h，随后进行三次喷淋，每次喷淋1 min，间隔1 min，至此为一个完整的冻融循环作用，具体试验过程如下：

将养护24 d的混凝土试件浸泡4 d，随后放入气候环境模拟试验箱，按照上述升降温机制及喷淋方式设定控制程序开始冻融试验；每25个冻融循环周期结束后(可根据实际损伤层变化规律对测试周期进行相应调整)，参照文献[14]中规定的损伤层测试方法进行混凝土冻融损伤层厚度测试，其检测原理如图1所示。图中，T为超声波探测仪发射换能器；R为接收换能器。

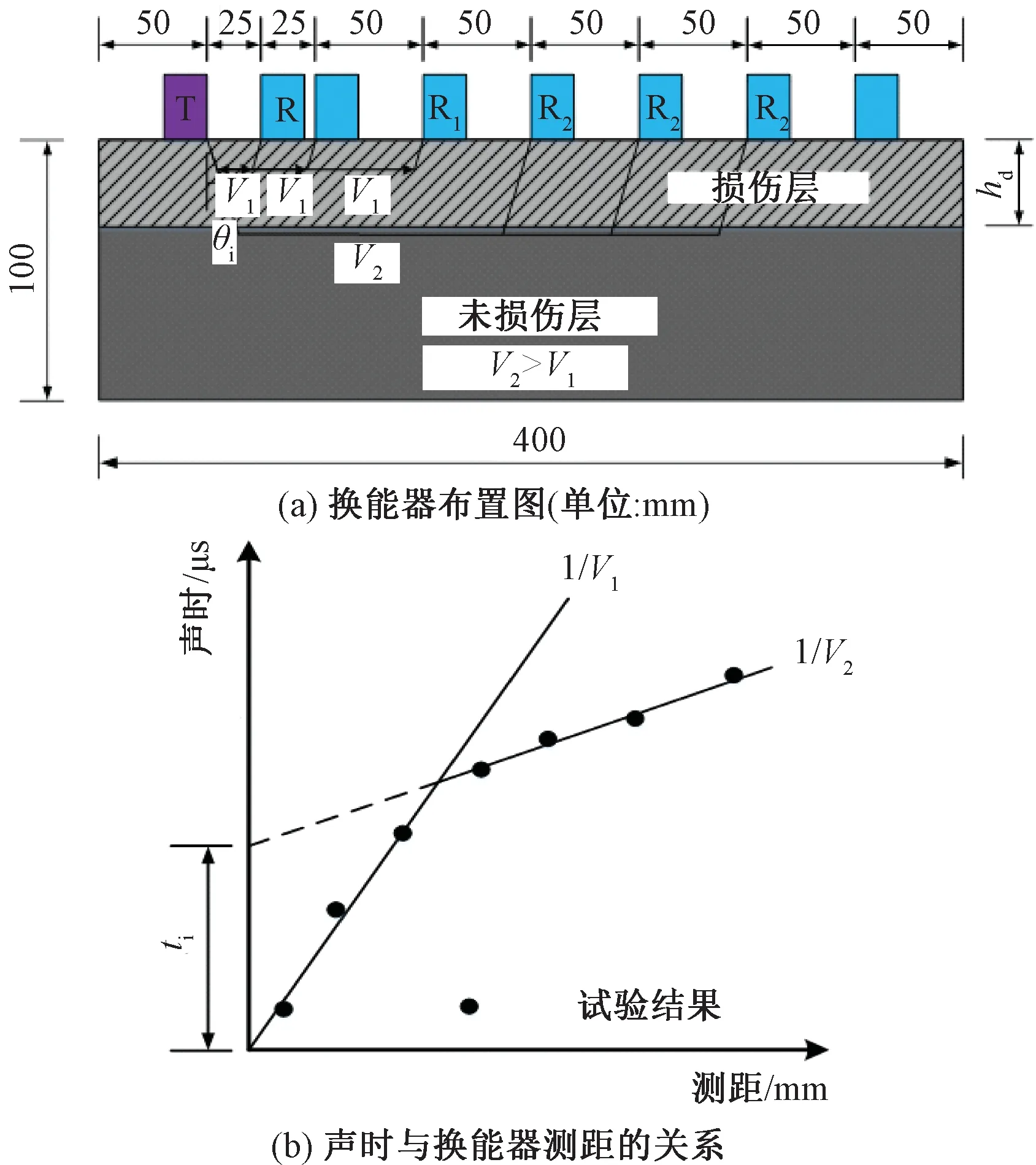
图1 损伤层厚度测试原理图

当冻融循环达到100、200、300次时，分别各取出3个棱柱体试件进行轴心受压试验，未取出试件继续进行冻融试验。轴心受压试验采用人工采点，采取加载过程中力和位移值。前期加载速率为0.2 mm/min，达到预估峰值70%后，加载速率降低为0.1 mm/min。为防止加载速率过快导致的突然破坏，在接近预估峰值时(90%的预估峰值)，加载速率可降低为0.05 mm/min，直至试验结束。

2 试验结果及分析

2.1 冻融损伤层厚度

依据图1中的损伤层厚度测试原理，可计算出不同冻融循环次数下混凝土损伤层厚度hd(N)为

(1)

式中：V1、V2分别为超声波在混凝土损伤层和未损伤层中的传播速度，即测距-声时关系中曲线斜率的倒数，如图1(b)中所示；ti为直线1/V2的截距，如图1(b)中所示。根据式(1)可计算出不同冻融循环次数时混凝土损伤层厚的变化规律如图2所示。

图2 不同水胶比混凝土冻融损伤层厚度

由图2可知，3种水胶比的混凝土试件损伤层厚度均随冻融循环次数的增加而增加，且水胶比越大损伤层厚度越大。损伤层厚度的变化规律反映了试件的损伤劣化情况，随着冻融次数增加，混凝土微观结构逐渐劣化，不断的有微裂缝产生、发展、汇集、成核，损伤层由表及里逐渐扩展。通过回归分析可得冻融环境混凝土损伤层厚度与冻融循环次数的定量关系为

hd(N)=5.901 8kwe0.002 2NR2=0.984 0

(2)

式中：N为冻融循环次数；kw为与混凝土水胶比w/c有关的材料参数，可由下式确定

kw=1.335 2-2.034 4(w/c)+2.815 6(w/c)2

R2=0.944 8

(3)

2.2 冻融后混凝土应力应变曲线

三组不同水胶比混凝土试件在不同冻融循环次数下的轴心受压应力-应变关系如图3所示。

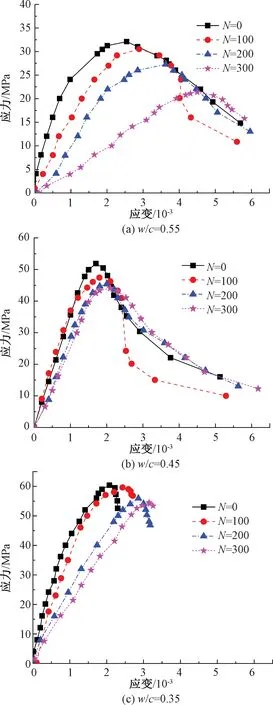
图3 冻融后应力-应变曲线

由图3可知，三组混凝土试件在气冻气融作用下的应力-应变曲线形态大致相似。随着冻融破坏不断加剧，混凝土峰值应力逐渐降低，峰值应变逐渐增大，这反映冻融加剧了混凝土初始损伤；此外，曲线趋于扁平，且水胶比越大曲线扁平率越高；水胶比0.35组试件强度较高，混凝土脆性行为显著，在曲线软化段时较之其他两组试件容易出现突然脆断的现象。

3 损伤本构模型的确定

3.1 损伤变量的确定

根据损伤力学相关理论，损伤变量是材料损伤演化行为及损伤程度的一种评价指标。因此，确定合理的损伤变量是评价混凝土冻融损伤度的关键问题。

冻融环境下混凝土抗压强度通常被用来评价冻融损伤度，但在实际工程中，对于既有混凝土结构而言，强度指标不宜获取(如钻芯取样，对结构有影响)。鉴于此，本文以既能反映冻融破坏特点，又便于工程检测，且对原结构无影响的损伤层厚度为评价标准。

在确定损伤变量的表达式前，作如下假设：①未冻融混凝土损伤度为0；②冻融损伤层厚度沿混凝土试件各方向均匀发展；③损伤层厚度范围内损伤度一致，不考虑其梯度变化。根据损伤力学的概念，混凝土冻融损伤变量D可以定义为

(4)

式中：Dh(N)为冻融损伤变量；b为试件截面宽度，mm；h为试件截面高度，mm。

为讨论混凝土冻融损伤层厚度所定义损伤度的可靠性，将不同评价指标定义的损伤度(即损伤变量)进行对比分析，结果如表2所示。表2中

(5)

式中：fcN、fc0分别为冻融N次与未冻融的混凝土抗压强度。

表2 不同指标损伤度分析

由表2可知，两种评价指标所定义的损伤度均随冻融循环次数的增加而增大，且水胶比越大，损伤度越大，符合一般规律。但损伤层所定义的冻融损伤度远大于强度指标所定义的损伤度，三组不同水胶比Dh/Df的平均值分别为：4.57(w/c=0.55)、3.79(w/c=0.45)、3.65(w/c=0.35)，分析出现该现象原因为：在用损伤层进行损伤度评估时，认为损伤层内材料完全损伤(即没有残余强度)，但实际上，冻融损伤是由表及里逐渐减弱的，也就是说损伤层范围内的混凝土并非完全没有强度。所以，此时以损伤层定义的损伤度较大。

另一方面，分别从每一组水胶比下的Dh/Df值纵向对比来看，随着冻融次数的增加，比值逐渐减小(越来越接近强度指标定义的损伤度)，最终趋于一个较为稳定的数值范围内，反映出采用超声波评测法检测损伤层厚度时，冻融损伤越小，误差越大；冻融损伤越大，误差越小，检测结果可靠性越高。

综上所述，用损伤层评价冻融损伤度时，需考虑损伤层范围内的残余强度，评价结果才能更准确。

3.2 考虑残余强度修正的损伤度

混凝土结构遭受冻融破坏时，损伤是由表及里逐渐减弱的，在损伤层范围内并不是完全损伤，而超声波无损检测法所测结果无法反映出这一特点，故需考虑损伤层范围内存在的残余强度，对所测结果进行相应的修正。

假定损伤层内混凝土的抗压强度是均匀的，记为fcr，冻融后整体混凝土的抗压强度为fcN，未冻融混凝土(未损伤层混凝土)的抗压强度为fc0；损伤层与未损伤层混凝土的本构关系不同，但其变形是协调的，通过变形的一致将两部分联系起来[15]。根据以上假定，冻融后混凝土材料在受压过程中外荷载是由损伤层(存在残余强度，还有承担荷载的能力)混凝土与未损伤层混凝土共同承担，则有

σcNAN=σc0A0+σcrAr

(6)

式中，σcN为冻融后整体混凝土(包括损伤层与未损伤层)的应力；σc0为未冻融混凝土(未损伤层混凝土)的应力；σcr为损伤层内混凝土剩余的平均应力；AN为冻融N次后混凝土截面积；A0为未损伤的混凝土截面积；Ar为损伤层混凝土截面积。

当外荷载达到破坏荷载时，有

fcNAN=fc0A0+fcrAr

(7)

考虑损伤层内的残余强度，引入损伤层厚度修正系数α，表达式为

(8)

则式(4)变为

(9)

修正后的冻融损伤度及其分别与未修正时的损伤度、强度指标定义的损伤度的比值如表3所示。

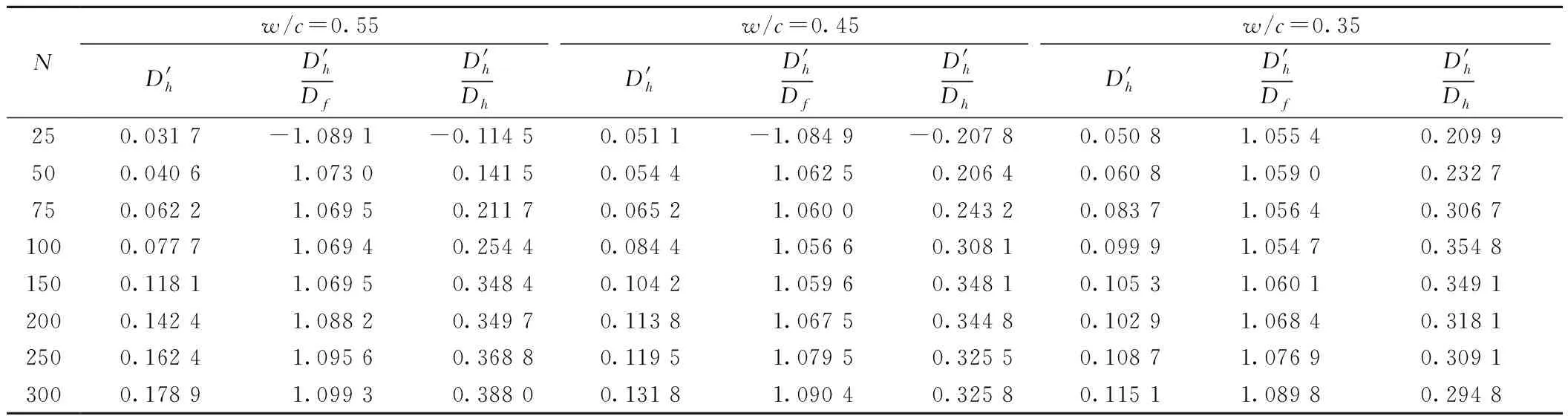
表3 修正后损伤度分析

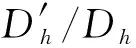
由此可见，考虑损伤层内残余强度，引入损伤层修正系数后的损伤评估结果可靠性明显提高。

3.3 修正系数α

损伤层残余强度修正系数α随冻融循环次数增加的变化规律如图4所示。

图4 α与冻融循环次数的关系

由图4可知，随着冻融次数的增大，修正系数α逐渐减小，且水胶比越大的修正系数减小的越多，这是因为修正系数与损伤层内残余强度正相关，随着冻融次数的不断增加，损伤不断累积，整个混凝土材料的强度与损伤层内的混凝土材料残余强度都在减小，相应地α不断减小，修正后的冻融损伤层厚度越来越接近检测所得损伤层厚度。另一方面，水胶比越大，初始强度越低，同时抗冻性越差，损伤层内残余强度损失越快，故修正系数也减小的越多。由此可见，修正系数α可用于描述混凝土遭受冻融作用后的损伤演化行为。

3.4 轴心受压损伤本构模型

在给出冻损混凝土轴心受压状态下的损伤演化方程(即同时考虑冻融损伤与受荷损伤)时，作如下假设：①混凝土的损伤是冻融损伤和受荷损伤的耦合；②混凝土损伤的主轴与应力主轴和应变主轴重合。考虑工程计算简便，本文以一种简单的双直线混凝土损伤模型为轴心受压状态下混凝土损伤演化方程，其表达式为

(10)

式中：Dc为轴心受压时混凝土损伤变量；ε为瞬时应变；εu为混凝土轴心受压时的极限应变；εc为混凝土轴心受压时的峰值应变；。

混凝土轴心受压损伤本构模型可表示为

σ=E0·ε·(1-Dc)

(11)

式中：E0为混凝土初始弹性模量。

引入修正后损伤层厚度所定义的冻融损伤因子，冻融后混凝土轴心受压损伤本构模型可表示为

(12)

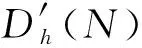
σ=E0·ε·(1-D)

(13)

(14)

3.5 混凝土损伤率的演化规律

混凝土轴心受压状态下损伤率为

(15)

将式(15)代入式(10)，可得

(16)

当冻融次数和由于荷载引起的应变逐渐增加时，两种因素引起的损伤也不断增加，混凝土的总损伤变化率可表示为

(17)

将式(9)、式(14)和式(16)代入式(17)，则可得出气冻气融作用后，混凝土轴心受压时总损伤率演化方程为

当0≤ε≤εc时

(18)

式中：α、β为待定系数，可通过试验确定。

当0≤ε≤εc时

(19)

冻融后不同水胶比混凝土试件轴心受压时应变与损伤之间的关系如图5所示。

图5 不同水胶比混凝土应变与损伤关系

由图5可看出，由于所采用的是双直线模型，应力-应变曲线上升段为线性，峰值点之前混凝土处于弹性阶段，无受荷损伤。随着冻融作用加剧，初始冻融损伤不断增大，峰值应变也不断增大；由图5(a)可知，峰值点后即应力-应变曲线下降段，初始冻融损伤度越大(遭受冻融循环次数更多)总损伤值的增加速率越大，即变化率更大；由图5(b)、图5(c)可知，混凝土抗压强度越大，峰值点后总损伤值的增加速率越大，尤其是水胶比0.35组混凝土试件损伤增加速率趋近于直线，这是因为强度越大，试件脆性破坏现象越显著，峰值点后试件迅速断裂破坏。

4 模型验证

为充分验证模型的通用性，将本文试验数据与文献[15]试验数据(水胶比均为0.45)带入式(2)、式(4)、式(13)与式(14)中，即可得模型计算出的应力-应变曲线，并与相应试验曲线进行比较，结果如图6所示。

图6 水胶比0.45组模型计算与试验应力-应变曲线

从图6可看出，所建立的混凝土冻融损伤本构模型与本文试验结果及文献[15]试验结果均吻合较好，验证了模型的一般通用性；此外，除图6(a)(未考虑冻融损伤)中模型拟合的应力略大于本文试验值外，图6(b)～图6(d)中模型拟合的应力普遍小于本文试验值。分析出现该现象的原因是：图6(b)～图6(d)中所示模型拟合曲线考虑了冻融损伤对应力-应变曲线的影响，且由式(14) 与表3可知，本文混凝土轴心受压损伤本构模型中的损伤因子可由修正后损伤层厚度所定义的损伤度确定，而该损伤度略大于强度指标定义的损伤度，即由修正后损伤层厚度定义的损伤度稍大于实际混凝土的冻融损伤程度，故相同应变时模型拟合应力值略小于试验应力值。

综上所述，使用该模型得到的结果偏于安全，符合模型在工程应用中需相对保守的特点，本文本构模型具有工程适用性。

5 结论

(1)考虑冻融损伤层内残余强度，引入修正系数后，以损伤层所定义的冻融损伤度与混凝土抗压强度所定义的冻融损伤度相近，即修正后的冻融损伤层厚度可较好地描述混凝土气冻气融作用下的损伤行为。

(2) 随着冻融作用加剧，损伤层修正系数α逐渐减小，反映出损伤层内残余强度不断减小，实际损伤度逐渐增大的行为。

(3)随着冻融循环次数的增加，考虑冻融损伤与受荷损伤的混凝土总损伤值增加速率逐渐增大；同时，混凝土抗压强度越大，总损伤值的增加速率越快。

(4)所建立的混凝土轴心受压冻融损伤本构模型与本文试验结果及其他文献试验结果均吻合较好，模型具有一定适用性。