2021年八省市联考第17题的探究与推广

广东省湛江一中培才学校(524037) 魏 欣

求数列的通项公式与数列求和是高考数学的重点考查内容.高考对数列的考查主要有两种形式,一种是直接利用公式或者构造法求等差、等比的通项公式与数列的前n项和公式,重点考查公式法、构造法、错位相减法、裂项相消法等知识.事实上,很多时候除了常用的数列的通项公式与数列求和方法外,还可以通过构造常数列去解决数列求通项求和问题.非零常数列身兼等差数列和等比数列两大特性,在一些数列求通项求和问题中,若能适时地构造常数列,则可避免复杂的累加、累乘或迭代等过程,从而使数列求通项求和一步到位,达到事半功倍的效果.

下面以2021年八省市联考第17 题为例,通过构造常数法的解答与分析,并进行探究与推广,总结出构造常数法巧解数列的通项公式与数列的前n项和的几种题型.

一、试题展示与解法探究

题目(2021年八省市联考第17 题)已知各项都为正数的数列{an}满足an+2=2an+1+3an.

(1)证明: 数列{an+an+1}为等比数列;

(2)若a1=求数列{an}的通项公式.

分析该题主要考查了等比数列的判定,根据数列的递推关系式求通项公式等知识,考查了学生分析问题、解决问题的能力及特殊与一般、转化与化归的数学思想,体现了逻辑推理、数学运算等数学核心素养.第(1)问通过对递推关系式的变形不难证明;第(2)问在第(1)问的基础上展开,通常解法为构造法.下面构造常数法求数列的通项公式.

解析(1)注意所证数列的结构特征暗示了证明方法.将an+2= 2an+1+3an两边都加上an+1得an+2+an+1=3(an+1+an), 因为数列{an}的各项为正数, 所以数列{an+an+1}是首项为a1+a2, 公比为3 的等比数列.以下第二问的两种解法.

解法1以第1 问所得结果为基础进行解答.

解法2由an+2= 2an+1+3an, 设an+2-µan+1=ν(an+1-µan),即an+2= (µ+ν)an+1-µνan,与已知等式比较得

当µ=-1 且ν= 3 时,an+2+an+1= 3(an+1+an),下同解法1,此处从略.

当µ= 3 且ν=-1 时,an+2-3an+1=-(an+1-3an).若a1=当n= 1 时,an+2-3an+1=a2-3a1== 0, 所以数列{an+1-3an}是恒为零的常数数列,所以an+1= 3an,故数列{an}是首项a1=公比为3 的等比数列,故数列{an}的通项公式为an=

二、教材寻根

教材题目(新课标人教版A 版《数学(必修5)》第二章复习参考题B 组第6 题) 已知数列{an}中,a1= 5,a2=2,an=2an-1+3an-2(n≥3),对于这个数列的通项公式作研究,能否写出它的通项公式?

解(构造法)由an=2an-1+3an-2,得an-3an-1=-(an-1-3an-2),而a2-3a1=-13,故数列{an+1-3an}是公比为-1,首项为-13 的等比数列,所以

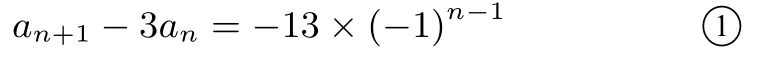
又由an=2an-1+3an-2,得an+an-1=3(an-1+an-2),而a2+a1=7,故数列{an+1+an}是公比为3,首项为7 的等比数列,所以

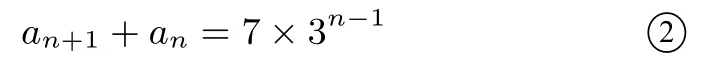
由①、②两式消去an+1, 得数列的通项公式为an=

三、提炼推广

(一)构造常数列求数列的通项公式

在数列{an}中,若an+1=an,n ∈N*,则称数列{an}为常数列,其通项公式为an=a1.

1 构造常数列推导等差数列通项公式

在等差数列{an}中,an -an-1=d,(n≥2,n ∈N⋆),则an-nd=an-1-(n-1)d,所以数列{an-nd}是一个常数列,即an-nd=a1-d,故an=a1+(n-1)d.用此方法还容易得到an-nd=am-md,即an=am+(n-m)d.

2 构造常数列推导等比数列通项公式

在等比数列{an}中,=q, (n≥2,n ∈N⋆).则所以数列是一个常数列,即故an=a1qn-1.用此方法还容易得到可得an=amqn-m.

评析等差、等比数列的通项公式的推导是数列教学的难点,教材分别采用累加法、累乘法推导其通项公式,对新学数列知识的同学要求较高.如果巧借常数列推导等差、等比数列的通项公式,似乎更好理解,而且给人耳目一新的感觉.

3 构造常数列巧求递推数列的通项

题型一an+1=pan+q,(p、q都是非零常数,p/=1)

定理1若an+1=pan+q(其中p、q都是非零常数,p /= 1), 则an+1- xpn - y=p(an-xpn-1-y), 数列{an-x·pn-1-y}是各项都为零的常数列, 且an=x·pn-1+y,其中x=

证明an+1=pan+q ⇔an+1-xpn=pan-xpn+q ⇔an+1-xpn -y=p(an-xpn-1-y)+q+y(p-1)(x,y是待定的常数).

设q+y(p -1) = 0, 且a1- x - y= 0, 则{an-x·pn-1-y}是各项都为零的常数列,所以数列{an}的通项公式为an=x·pn-1+y.由于q+y(p-1) = 0,所以y=因为a1-x-y=0,所以x=a1-所以定理1 得证.

例1(2014年高考全国ⅠⅠ卷) 数列{an}中,a1= 1,an+1=3an+1,求{an}的通项公式.

解因为an+1= 3an+1, 所以an+1-即an+1-因为a1= 1, 所以= 0, 所以数列是各项均为零的常数列, 所以=0,所以数列{an}的通项公式为an=

注释由定理1, 知a1= 1,p= 3,q= 1,x=数列{an}的通项公式为an=x·pn-1+y=

例2(2006年高考江西卷理科节选)已知数列{an}满足:a1=(n ∈N*).求数列{an}的通项公式.

解因为an+1=所以an ＞0,因为所以数列是各项都为零的常数列,所以数列{an}的通项公式an=

注释把看成an, 则就看成a1,就看成an+1.比较,an+1=pan+q可见由定理1 知

题型二an+1=an+rn-1,(r ＞0 且r /=1).

定理2若an+1=an+rn-1(r ＞0 且r /= 1), 则an+1-x·rn-y=an-x·rn-1-y,{an-x·rn-1-y}是各项都为零的常数列,an=x·rn-1+y,其中x=

证明an+1=an+rn-1⇔an+1-x·rn-y=anx·rn-1-y,其中x,y是待定的常数,且满足a1-x-y=0,则数列{an-x·rn-1-y}是各项都为零的常数列, 所以an=x·rn-1+y.因为an+1-x·rn-y=an-x·rn-1-y ⇔an+1=an+x(r -1)·rn-1⇔an+1=an+rn-1, 所以x(r -1) = 1,x=因为a1- x - y= 0, 所以y=a1-定理2 得证.

例3(2008年高考天津理科节选) 在数列{an}中,a1=1,a2=2,且an+1=(1+q)an-qan-1(q /=0).

(Ⅰ)设bn=an+1-an(n ∈N*),证明:{bn}是等比数列;(ⅠⅠ)求数列{an}的通项公式.

解(Ⅰ){bn}是首项为1,公比为q的等比数列,过程从略.

(ⅠⅠ)an+1-an=qn-1,(1)当q= 1 时an+1-an= 1.因 为a1= 1, 所 以an= 1 + (n -1)·1 =n.(2) 当q /= 1 时, 因an+1-an=qn-1, 所以an+1=an+qn-1,an+1-因为a1= 1,所以数列是各项都为零的常数列,an=综上所述,数列{an}的通项公式为an=

注释对比an+1=an+qn-1与an+1=an+rn-1可得r=q.因为a1= 1, 所以由定理2 知:x=这种方法回避了叠加法,简化了解题过程.

题型三an+1=pan+rn+1,其中p,r都是非零常数.

定理3若an+1=pan+rn+1(p,r都是非零常数,p /= 1,p /=r,r ＞0,r /= 1), 则an+1-x·pn -y ·rn+1=p(an-x·pn-1-y·rn),数列{an-x·pn-1-y·rn}是各 项 都 为 零 的 常 数 列,an=x · pn-1+y · rn, 其 中

证明an+1=pan+rn+1,所以an+1-x·pn-y·rn+1=p(an-x·pn-1-y·rn), 其中, 令a1- x - yr= 0, 则{an-x·pn-1-y·rn}是各项都为零的常数列.所以an=x · pn-1+y · rn, 因为an+1- x · pn - y · rn+1=p(an-x·pn-1-y·rn),⇔an+1=pan+y(r-p)·rn ⇔an+1=pan+rn+1,所以y(r-p) =r,即取y=由a1-x-yr=0,所以x=a1-定理3 得证.

例4(2006年高考全国Ⅰ理科节选)设数列{an}的前n项的和Sn=(n ∈N*).求数列{an}的通项公式.

解因为Sn=所以a1=a1=2,因为Sn=所以所以Sn+1-Sn=

所 以an+1= 4an+ 2n+1,an+1-4·4n -(-1)·2n+1=4[an-4·4n-1-(-1)·2n], 所以an+1-4n+1+2n+1=4(an-4n+2n), 因为a1= 2, 所以a1-4+2 = 0, 数列{an-4n+2n}是各项都为零的常数列,数列{an}的通项公式为an=4n-2n.

注释对比an+1= 4an-2n+1与an+1=pan+rn+1可见:p= 4,r= 2.因为a1= 2, 所以由定理3 知:

题型四f(n)an+1=g(n)an,其中f(n)、g(n)都是关于n的表达式,f(n)·g(n)/=0.

思路先根据a1,a2,a3的值猜想出an, 再对f(n)an+1=g(n)an直接进行恒等变形.

例5(2018年高考全国Ⅰ卷文科第17 题节选)已知数列{an}满足a1= 1,nan+1= 2(n+1)an,求数列{an}的通项公式.

解因为nan+1= 2(n+ 1)an, 所以nan+1-n(n-1)2n= 2(n+ 1)an - n(n-1)2n, 所以n[an+1-(n-1)2n]=2(n+1)[an-n2n-1],因为a1=1,所以a1-1×21-1= 0,所以数列{an-n2n-1}是各项都为零的常数列,数列{an}的通项公式为an=n2n-1.

例6(2012年高考全国卷文科节选)已知数列{an}的前n项和Sn=,(n ∈N*),a1= 1.求数列{an}的通项公式.

解因为Sn=, 所以Sn+1=所以an+1=,nan+1= (n+2)an, 所以因为a1= 1, 所以a1-是各项都为零的常数列, 所以数列{an}的通项公式为

这种方法回避了迭乘法,简化了解题过程.

题型五an+1=λan+f(n),其中λ/=0.

对于递推关系式为an+1=λan+f(n)(λ /= 0)的数列,求其通项公式时,我们可以构造常数列{bn},通过通项bn求得通项an.

(1)当λ=1,f(n)为常数时,数列{an}为等差数列,利用公式求通项.

(2) 当λ= 1,f(n) =pn+q(p,q为常数,p /= 0) 或f(n) =pqn+r(p,q,r为常数,p /= 0,q /= 1),可利用累加法求通项.

(3) 当λ /= 1,f(n) =pn+q(p,q为 常 数) 时, 构造常数列{bn}, 设bn=由bn+1=bn及an+1=λan+f(n), 得解得,即再由首项a1得通项bn,整理得通项an.

(4)当λ/=1,f(n)=pqn+r(为常数,p/=0,q /=1)时:

①若λ=q,递推关系式整理为

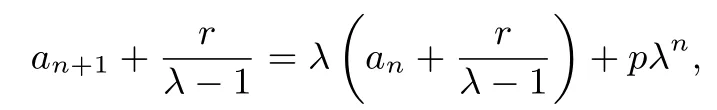
则

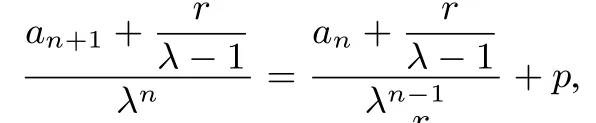
转化为公差为p的等差数列求通项问题;

②若λ/=q,构造常数列{bn},设bn=由bn+1=bn及an+1=λan+f(n),得

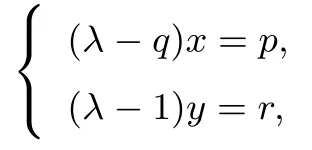
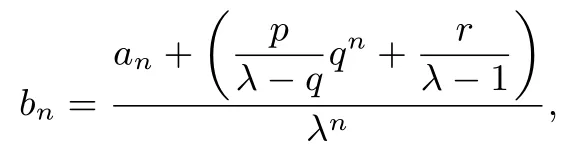
再由首项a1得通项bn,整理得通项an.

例7(2021年八省市联考第17 题) 用构造常数列法.由(1) 知数列{an+an+1}是首项为a1+a2, 公比为3 的等比数列.则有an+an+1= 2·3n-1.构造常数列{bn},满足bn=即an+1+an=-4x3n-2y,又an+an+1=23n-1, 所以所以bn=

例8(2020年高考全国Ⅲ卷理科第17 题节选)设数列{an}满足a1=3,an+1=3an-4n.求数列{an}的通项公式.

解构造常数列{bn},满足bn=于是即an+1= 3an+2xn-x+2y,又an+1=3an-4n,则解得所以bn=所以数列{an}的通项公式为an=2n+1.

例9(2013年高考广东卷理科节选)设数列{an}的前n项和为Sn,a1=1,

(Ⅰ)求a2的值;(ⅠⅠ)求数列{an}的通项公式.

解(Ⅰ)a2=4,过程从略.(ⅠⅠ)因为所以2Sn=nan+1-当n≥2 时,2Sn-1=(n-1)an-所以2Sn-2Sn-1=nan+1-(n-1)an -所以2an=nan+1-(n-1)an -n(n+1),所以nan+1=(n+ 1)an+n(n+ 1), 所以n[an+1-(n+1)2]= (n+1)(an-n2), 所以an=n2(n≥2), 因为a2= 4, 所以a2-22= 0,数列{an-n2}(n≥2)是各项都为零的常数列,所以数列{an}的通项公式为

因为a1=1 也适合(1)式,所以an=n2(n ∈N*).

例10(2014年高考广东卷理科节选) 设数列{an}的前n项和为Sn, 满足:Sn= 2nan+1-3n2-4n(n ∈N*),S3=15.求数列{an}的通项公式.

解容易得a1=3,a2=5,a3=7.因为Sn=2nan+1-3n2-4n,所以Sn+1=2(n+1)an+2-3(n+1)2-4(n+1),Sn+1-Sn= 2(n+1)an+2-2nan+1-3(n+1)2+3n2-4(n+1)+4n,an+1=2(n+1)an+2-2nan+1-6n-7,(2n+2)an+2=(2n+1)an+1+6n+7,(2n+2)[an+2-(2n+5)]=(2n+ 1)[an+1-(2n+3)].因为a2= 5, 所以n≥2 时,a2-5=0,数列{an-(2n+ 1)}(n≥2)是各项都为0 的常数列,所以数列{an}的通项公式为

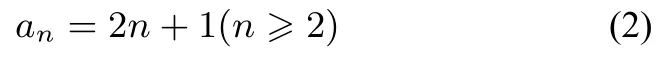
因为a1=3 也适合(2)式,所以an=2n+1(n ∈N*).

(二)构造常数列巧求数列的前n 项和

1 等比数列{an}的前n 项和,其中公比q /=1.

由an=a1qn-1=(qn-qn-1), 可得Sn=(qn-qn-1), 即Sn -=Sn-1-故数列为常数列, 因为Sn -所以Sn=

评注等比数列的求和公式我们一般用“错位相减法”推导,运用构造常数列来求和则极大的减小了这类求和的运算复杂性.

2 利用构造常数列巧求形如an = (kn + b)qn(k /=0,q /=0,1)的数列的前n 项和.

一般地, 除了用常规的“错位相减法”求其前n项和以外,还可以用如下方法转化为常数列: 由an=Sn-Sn-1,得Sn=Sn-1+(kn+b)qn,令Sn+(xn+y)qn=Sn-1+[x(n-1)+y]qn-1,则Sn=Sn-1+-y]qn,比较系数,得-y=b,联立解得:x=故{Sn+(xn+y)qn}为常数列, 进而求出Sn.

例11(2020年高考全国Ⅲ卷理科第17 题节选)设数列{an}满足a1= 3,an+1= 3an -4n.求数列{2nan}的前n项和Sn.

解由题知n≥2 时,Sn - Sn-1= (2n+ 1)2n, 设Sn -(xn+y)2n=Sn-1-(x(n -1) +y)2n-1, 整理得Sn-Sn-1=(xn+x+y)2n-1,则xn+x+y=2(2n+1),得所以Sn-(4n-2)2n=Sn-1-[4(n-1)-2]2n-1,因此数列{Sn-(4n-2)2n}常数列,又S1-(4-2)×2=2,所以Sn-(4n-2)2n=2,故Sn=(2n-1)2n+1+2.

例12(2018年高考浙江卷节选)已知等比数列{an}的公比q ＞1,且a3+a4+a5=28,a4+2 是a3,a5的等差中项.数列{bn}满足b1= 1,数列{(bn+1-bn)an}的前n项和为2n2+n.

(1)求q的值;(2)求数列{bn}的通项公式.

解(1)q=2.过程略.

(2) 设cn= (bn+1-bn)an, 数 列{cn}前n项和Sn,由cn=解得cn= 4n-1,由(1)知an= 2n-1, 所以bn+1- bn= (4n -1)·设bn+1-(kn+b)·则bn+1- bn=与式子bn+1- bn= (4n -比较, 得解得所以bn+1+(8n+14)=bn+[8(n-1)+14]即数列是常数列, 所以bn+ [8(n -1) + 14]=b1+ 14 = 15, 故bn=

例13(2018年高考天津卷理科)已知数列{an}为等差数列,前n项和Sn,{bn}是首项为2 的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.

(1)求{an}和{bn}的通项公式;(2)求数列{a2nb2n-1}的前n项和Tn.

解析(1)bn=2n,an=3n-2.过程略.

(2) 由题知n≥2 时,Tn - Tn-1= (3n-1)4n, 设Tn -(xn+y)4n=Tn-1-(x(n-1)+y)4n-1, 整理得Tn - Tn-1= (3xn+x+3y)4n-1, 则3xn+x+ 3y=4(3n-1),得3x=12,x+3y=-4,解得x=4,y=所以Tn-,因此数列为常数列,又所以Tn -故

(三)利用构造常数列巧求“裂项相消法”的数列的前n项和.

一般地,除了用常规的“裂项相消法求和”求其前n项和以外,还可以用如下方法转化为常数列: 若数列{an}为每一项都不为零的等差数列,设数列bn=则数列{bn}的前n项和

证明设数列{an}的公差为d,若d=0,则所述等式显然成立.若d /= 0,因为则Tn -Tn-1=bn=即Tn -Tn-1=所以Tn+所以数列为常数列,所以

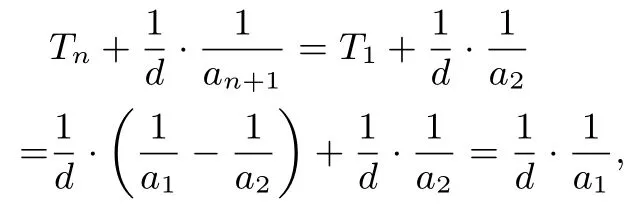
所以

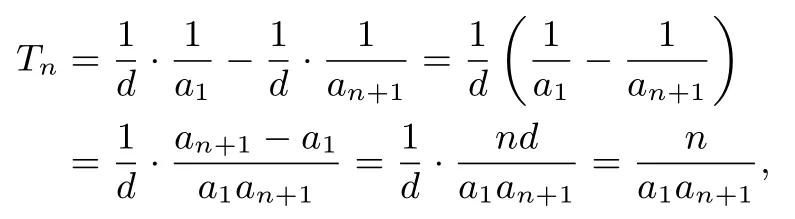
例14(2017年高考全国Ⅲ卷文科) 数列{an}满足a1+3a2+···+(2n-1)an=2n.

(1)求{an}的通项公式; (2)求数列的前n项和.

解(1)an=过程略.(2) 设bn=则bn=设数列的前n项和为Sn,当n≥2,bn=Sn-Sn-1=即所以数列是常数列, 又S1=所以

例15(2016年高考全国卷)已知数列{an}的前n项和Sn=n2.

(1)求{an}的通项公式;(2)记bn=求数列{bn}的前n项和Tn.

解(1)an=2n-1,过程略.

(2)则Tn=Tn-1+所以Tn -=Tn-1-故数列为常数列,所以

例16(2014年高考山东卷理科)已知等差数列{an}的公差为2,前n项和为Sn,且S1,S2,S4成等比数列.

(1)求数列{an}的通项公式;

(2)令bn=求数列{bn}的前n项和Tn.

解(1)an=2n-1,过程略.

(2)

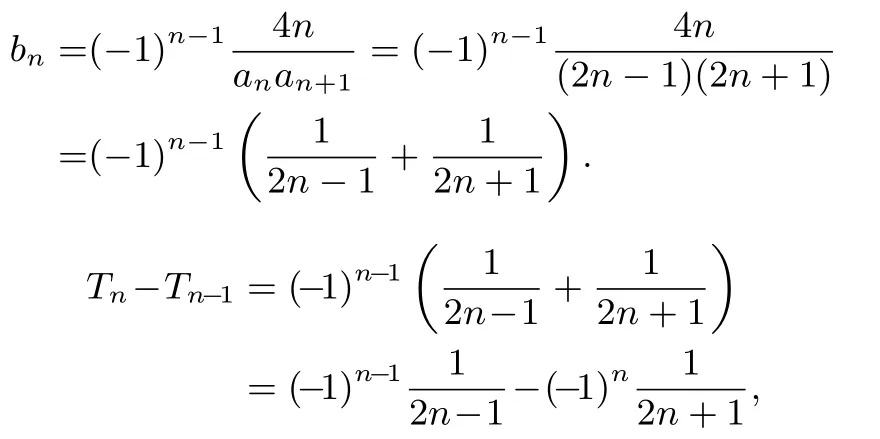
四、教学建议

通过构造常数列求数列的通项与求和,给我们提供了解决数列的通项公式与数列求和问题的另外一种途径,值得指出的是,在实际解题中,我们应该根据实际情况或自己对方法的掌握程度,去选择最佳的求和方法,不能一味地追求变常数列,这样可能反而降低了学习数学的效率,减弱了数学解题的多样性和对解题方法的掌握.

对照近几年的全国卷高考试题,可以发现几乎每一道都可以从教材中找寻到“源头”, 它们或是课本习题的简单变式,或是重组,又或是拓展等,清楚地呈现出“题在书外,根在书中”.课本上的例习题是对基本知识的考查,是教材中每一个概念、每一个公式、每一个定理的检验依据.通过对课本例题、习题的变形、改编和拓展,揭示例题、习题与高考题的联系,探寻高考题的解题方法和规律.