圆锥曲线几个结论的拓展、变式及推广
福建省莆田第五中学(351100) 宋桂芳
文[1]对2015年全国高考北京卷第19 题进行了本质探究和推广,得到了关于椭圆、双曲线的3 个结论,读后觉得意犹未尽.本文先将这些结论拓展到抛物线的情形,再给出这些结论的等价变式及部分等价变式的推广.首先将[1]的这3 个结论抄录如下:
结论1(综合文[1]的结论1,2)已知椭圆C:1(a >b >0) 上一点P(x0,y0),A(m,n) 为椭圆C上一动点, 点A关于x轴(y轴) 的对称点为B, 若直线PA与x轴(y轴) 交于点M, 直线PB与x轴(y轴) 交于点N, 则|OM|·|ON|=a2,如图1(|OM|·|ON|=b2,如图2).
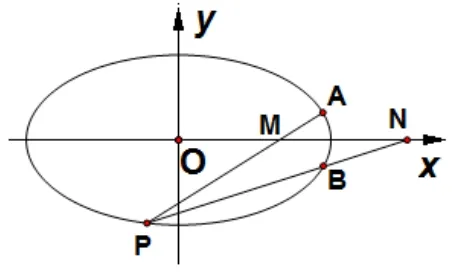
图1

图2
结论2(文[1]的结论3)已知双曲线1(a >0,b >0)上一点P(x0,y0),A(m,n)为双曲线C上一动点,点A关于x轴(y轴)的对称点为B,若直线PA与x轴(y轴) 交于点M, 直线PB与x轴(y轴) 交于点N, 则|OM|·|ON|=a2,如图3(|OM|·|ON|=b2,如图4).

图3

图4
1 结论的拓展
以上结论只涉及椭圆、双曲线,那么,对于抛物线,有没有类似的结论? 经探究,可得
结论3已知抛物线C:y2=2px(p >0)(x2=2py(p >0)上一点P(x0,y0),A(m,n)为抛物线C上一动点,与点P不关于x轴(y轴)对称,点A关于x轴(y轴)的对称点为B,若直线PA与x轴(y轴)交于点M,直线PB与x轴(y轴)交于点N,则|OM|=|ON|.
证明对于抛物线C:y2= 2px(p >0), 由条件知B(m,-n), 直线PA,PB的方程分别为y - y0=(x-x0),y -y0=·(x-x0).分别令y=0,可得则

又由P(x0,y0),A(m,n)在抛物线C上知= 2px0,n2=2pm,则2n2x0-= 2x0·2pm-2m·2px0= 0,从而=0.又易知点M,N在y轴异侧,即异号,从而有|OM|=|ON|.
相仿地,可以证明C:y2= 2px(p >0)也具有相应性质,限于篇幅,此处从略.证毕.
2 结论的等价变式
在上述结论中,由于点A,B关于x轴(y轴)对称⇔直线NA,NB(即NP)的斜率k1,k2满足k1+k2=0,故上述结论可分别等价表示为结论1′,2′,3′:
结论1′已知椭圆=1(a >b >0)上一点P(x0,y0),A(m,n)为椭圆C上一动点(与点P不关于x轴(y轴)对称),直线PA与x轴(y轴)交于点M,点N在x轴(y轴)上,若直线NA,NP的斜率k1,k2满足k1+k2= 0,则|OM|·|ON|=a2(|OM|·|ON|=b2).
结论2′已知双曲线C:= 1(a >b >0)上一点P(x0,y0),A(m,n) 为双曲线C上一动点(与点P不关于x轴(y轴) 对称), 直线PA与x轴(y轴) 交于点M,点N在x轴(y轴)上,若直线NA,NP的斜率k1,k2满足k1+k2=0,则|OM|·|ON|=a2(|OM|·|ON|=b2).
结论3′已知抛物线C:y2= 2px(p >0)(x2=2py(p >0)) 上一点P(x0,y0),A(m,n) 为抛物线C上一动点(与点P不关于x轴(y轴)对称),直线PA与x轴(y轴)交于点M,点N在x轴(y轴)上,若直线NA,NP的斜率k1,k2满足k1+k2=0,则|OM|=|ON|.
3 部分等价变式的推广
经探究发现,结论1′,2′中有关“x轴”的情形及结论3′可以推广到更一般的情形.
结论Ⅰ已知椭圆C:= 1(a >b >0)上一点P(x0,y0),A(m,n)为椭圆C上一动点(与点P不关于x轴对称),直线PA与x轴交于点M,点N在x轴上,点N1在过点N且垂直于x轴的直线上(不在直线PA上),若直线N1A,N1P,N1M的斜率k1,k2,k3满足k1+k2= 2k3, 则|OM|·|ON|=a2.
证明设直线PA的方程为x=ry+s(r /= 0), 与椭圆C的方程联立,得b2(ry+s)2+a2y2-a2b2=0,整理得(a2+b2r2)y2+2b2rsy+b2(s2-a2)=0.据韦达定理,得

易知直线PA与x轴交点M(s,0), 设N(u,0),N1(u,t), 则又由x0=ry0+s,m=rn+s得

又由k1+k2=2k3及k3=可得
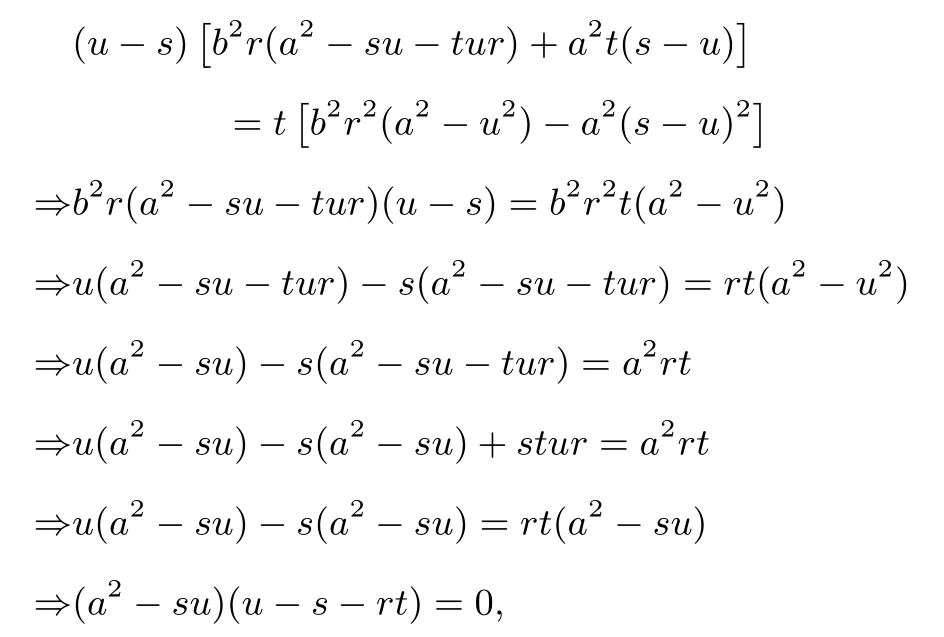
由于点N1(u,t) 不在直线PA:x=ry+s(r /= 0) 上,得u - s - rt /= 0, 则a2- su= 0.从而有s=进而得|OM|=又由N(u,0) 得|ON|=|u|, 故|OM|·|ON|=a2.证毕.
类似地,结论2′中有关“x轴”的情形及结论3′可分别推广为
结论ⅠⅠ已知双曲线C:= 1(a >0,b >0)上一点P(x0,y0),A(m,n)为双曲线C上一动点(与点P不关于x轴对称),直线PA与x轴交于点M,点N在x轴上,点N1在过点N且垂直于x轴的直线上(不在直线PA上),若直线N1A,N1P,N1M的斜率k1,k2,k3满足k1+k2=2k3,则|OM|·|ON|=a2.
结论ⅠⅠⅠ已知抛物线C:y2= 2px(p >0)(x2=2py(p >0)) 上一点P(x0,y0),A(m,n) 为抛物线C上一动点(与点P不关于x轴(y轴) 对称), 直线PA与x轴(y轴) 交于点M, 点N在x轴(y轴) 上, 点N1在过点N且垂直于x轴(y轴) 的直线上(不在直线PA上), 若直线N1A,N1P,N1M的斜率k1,k2,k3满足k1+k2= 2k3, 则|OM|=|ON|.
下面只证明结论ⅠⅠⅠ,结论ⅠⅠ仿结论Ⅰ可证.
证明设直线PA的方程为x=ry+s(r /= 0), 与抛物线C的方程联立并整理, 得y2-2pry -2ps= 0.据韦达定理, 得y0+n= 2pr,y0n=-2ps.易知直线PA与x轴交点M(s,0), 设N(u,0),N1(u,t), 则k3=又由x0=ry0+s,m=rn+s.得
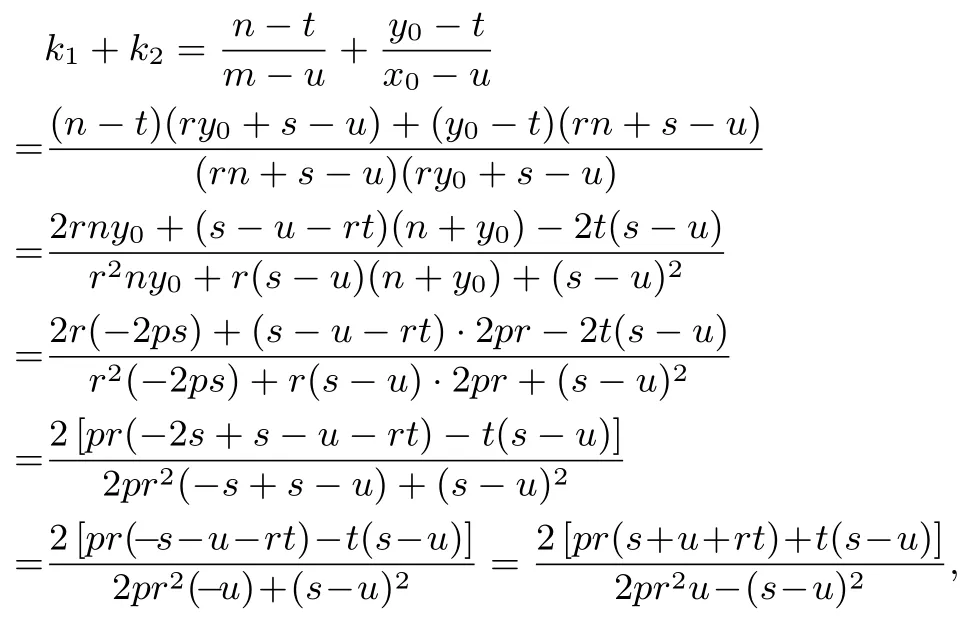
又由k1+k2=2k3及k3=可得
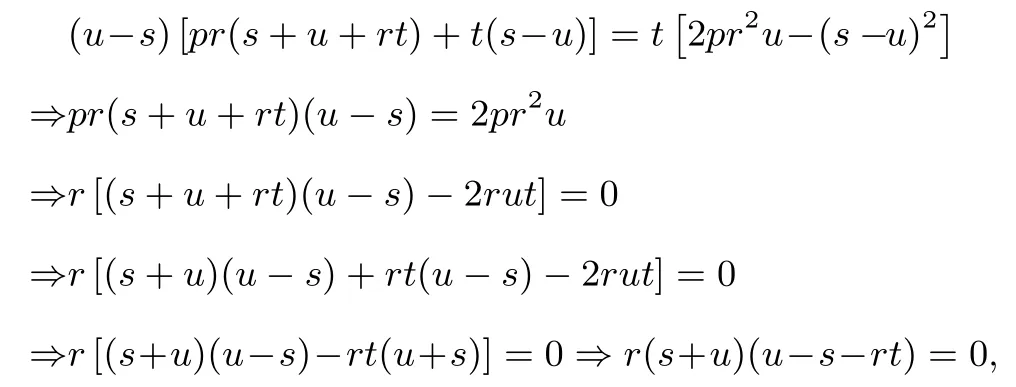
由于r /= 0 且点N1(u,t)不在直线PA:x=ry+s(r /= 0)上得u - s - rt /= 0, 故s+u= 0, 从而有|s|=|u|, 即|OM|=|ON|.证毕.
特别地,当点N1重合于点N时,结论Ⅰ,ⅠⅠ分别为结论1,2 中有关“x轴”的情形,结论ⅠⅠⅠ为结论.
至此,我们完成了对文[1]的3 个结论的拓展、变式及推广.

