核酸检测背后的数学原理
福建省石狮市第三中学(362700) 李 榕
新冠疫情爆发以来,我国在武汉、北京、新疆等地开展全员新冠病毒核酸检测筛查.面对数量巨大的检测样本我们采用了混合检测方式,这样的方式是否有效合理? 本文以数学建模的方式探究核酸检测过程中的数学问题,从而解释核酸检测背后的数学原理.
关键字 核酸检测;混合检测;均值不等式;二项分布
一、问题的提出
2020年5月11日武汉市下发《关于开展全市新冠病毒核酸筛查的紧急通知》,要求在10 天之内,对全武汉人员做一次核酸检测,彻底摸清武汉市的人员感染新型肺炎病毒的详细情况.
在新冠肺炎疫情防控期间,利用核酸检测出武汉市存在的确诊病例对早日战胜疫情来说至关重要.然而核酸检测确诊病例最快的话也需要几个小时,因此检测策略的效率将直接影响疫情的防空和确诊病人的救治.面对我国这样巨大的检测人数压力以及庞大的公共卫生经济资源的压力,去探究一种有效的解决途径势在必行.
2020年6月2日,湖北省新冠病毒肺炎疫情防控工作指挥部召开新闻发布会,介绍武汉市在十天内集中核酸检测排查结果,如下表[1]:

武汉市新冠病毒核酸检测“十天大会战”情况
为什么说657.4 万的检测试剂数量完成了武汉约1000万人全员排查的呢? 面对大于1 千万人数的检测需求,武汉一天需要完成超百万的检测量,这样的艰难目标到底如何去实现? 其中核酸检测的背后数学原理是什么呢?
二、数学模型
(一)模型假设:
1.新冠病毒核酸检测试剂的判断正确率为100%.
2.新冠病毒核酸检测试剂同样可以正确检测出混合样本,当混合样本的人均为阴性时则显现阴性特性,否则显示阳性特征.
3.假设每个人的取样足够多,且分组之后不影响最终检测结果.
4.假设武汉各地区感染情况是均匀分布的,且病毒总体感染率为p
(二)数学记号:
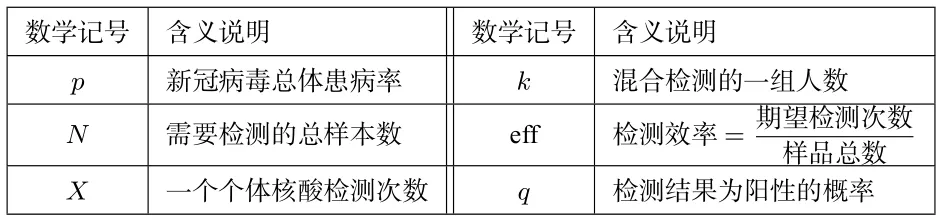
数学记号含义说明数学记号含义说明________________p 新冠病毒总体患病率k 混合检测的一组人数N 需要检测的总样本数eff 检测效率= 期望检测次数样品总数X 一个个体核酸检测次数q 检测结果为阳性的概率____
(三)模型建立与求解
1.初步探究问题
假设武汉各地区感染情况是均匀分布的,现对某社区进行新冠病毒核酸检测,全员100 人采集样本后,每20 个样本为一组,每组内的20 个样本混合起来,这样共得到5 组样本.若某个组的混合样本检测为阳性,则对这组的20 人再去进行逐一检测.记该社区检测总次数为η,且各组之间相互独立.求一个混合样本为阳性的概率q及其该社区检测总次数η分布列和期望.
2.初步探究结论
共需要检测多少次? 写出所有可能的次数.
·5 组都是阴性,则共需要5 次检测;
·1 组是阳性,4 组阴性,则共需要5+20 次检测;
·2 组是阳性,3 组阴性,则共需要5+20+20 次检测;
·3 组是阳性,2 组阴性,则共需要5+20+20+20 次检测;
·4 组是阳性,1 组阴性,则共需要5+20+20+20+20 次检测;
·5组是阳性,0 组阴性,则共需要5+20+20+20+20+20 次检测.
可得一组混合样本检测为阴性的概率为(1-p)20,阳性的概率为q=1-(1-p)20,η可能的取值为5,25,45,65,85,105.概率分布列图如下:

η 5 25 45 65 85 105 P C05(1-q)5 C15(1-q)4q C25(1-q)3q2 C35(1-q)2q3 C45(1-q)q4 C55q5
假设共有Y组检测结果为阳性,则Y ~B(5,q).因此E(Y)=5q.又由于随机变量η与Y的关系可得:
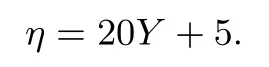
所以社区检测总次数为η的数学期望为:

3.再探究问题
4.再探究结论
易知,单次核酸检测效率为1,即每个个体所需的检测次数为1 次,一般来说个体平均需要检测的次数往往低于1.所以只需要求出每个个体的核酸检测次数X的数学期望,如果数学期望小于1,说明每个个体的检测次数平均小于1,也即混合检测的策略能够提高检测效率.同时每个个体的核酸检测次数X的取值只可能有两种:因此可以说随机变量X服从二项分布:
如果混合样本检测结果为阴性,k人平均测试即:

如果混合样本检测结果为阳性,k人平均测试次,即:

可得X的数学期望:

根据实际情况可知p非常小,同时根据二项式定理有:
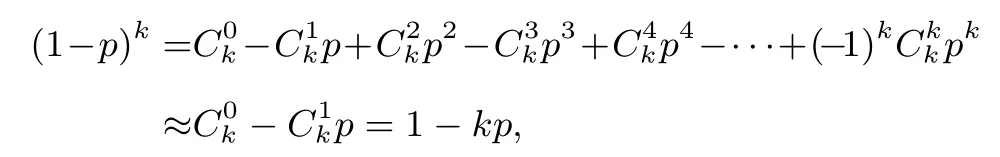
所以有:

依据武汉卫健委公布数据: 武汉约1000 万人口, 约8万人感染新冠病毒, 感染率p约为0.008, 四舍五入可以取p=0.01 代入式(1)为:
随着社会的发展,技术的进步,可能现在孩子学的许多东西到二三十年后就没有用了,但是让孩子做最好的自己,可以让他们受益一辈子。

显然E(X) 越小越好, 根据均值不等式可得当且仅当时,即k= 10 时,E(X)取最小值0.2.也就是说平均单人只需要检测0.2 次,这约节省了80%的成本.实际上,武汉市的部分区域正是一次性将10 人的样本混合在一起作为一组进行检测,从而提高检测效率.
武汉市十天大会战需要核酸检测的人数约为1000 万,如果每天可以检测10 万人次的话,单次检测则需要100 天(3 个多月).但是如果采取混合检测的策略,就可以通过数学方法解决了这个棘手的问题.假设如上方法武汉市每10 人一组进行混检,只需要10 天便可以完成全武汉一千万人的核酸检测.
三、评价与改进
以上模型通过数据运算说明了在保证正确率的前提下,最佳的混合检测样本数.但是以上的结果当然只是理论上的期望估计值,实际检测过程还有很多制约和干扰因素,比如,在疫情严重的地方我们可以采取单一检测的方法,在病毒感染率较高情况下可以采取混合检测的方法,以此提高效率.
核酸检测过程中我们还可以在此地方进行改进:
(一)适当缩小混合组,这即可以减小混合样本过多检不准的问题, 还可以减少一个组中可能包含两个阳性的概率.实际上武汉是使用这种方式,将5 10 人的样本作为一组进行混合检测。
(二)排除实践中阳性不会呈现完全均匀分布问题的对检测的干扰.我们可以根据以往的新型肺炎感染率,同时可以先将整个待测地进行预采样,得到此片区的整体平均感染率.针对低阳性率的地区用多人分组混合检测,较高阳性率的地区可以采用两三人一组为混合检测.疫情最严重的地区可以采用逐一检测,即1 人1 测.
(三)重视从技术上解决个别误检问题.在假设误检概率不是很大时,现在采取重复检测方法,如果有2 个检测结果为阳性的话,则最后判定为阳性.这样的话一次误检的结果也不会影响最后的结果.
四、探究推广与应用
实践和理论分析表明,当大量的待检测样本中含阳性样本较少时,如高考考生体检验血、新兵入伍复查体检验血,组合检测法比逐一检测法需要的检测次数要少.反之如果所有样本中阳性的比较多,那么组合检测法很有可能不仅不会减少检测的次数,还会增加检测的次数.根据Hu-Hwang-Wang猜想: 若已知有1/3 以上的样本是坏的,则逐一检测法是最好的[2].

