基于单轴磁传感器的旋转弹姿态解算算法

严 浩，袁 磊

(1.北京理工大学机电学院，北京 100081；2.北京特种车辆研究所，北京 100072)

0 引言

在弹体设计以及弹体空气动力学研究中，弹体的飞行姿态参数测量是必不可少的，准确地对弹体飞行姿态进行测试对推动弹体的设计进程有重大意义。使用陀螺仪进行高速旋转弹体姿态测量，测量结果误差大、成本高。磁传感器具有成本低、体积小、抗过载高、灵敏度高的优点，多用于航向估计，使用磁传感器对旋转弹体测姿有研究价值。采用机载磁传感器精确测量旋转体的姿态一直被认为是一项艰巨的任务[1]。文献[2]建立了数学模型，提出了利用地磁信息求解地磁偏角的方法，但是数学模型应用范围受限较大，且没有进行误差分析。文献[3]在Harkins等人研究基础上，提出了磁传感器选择、安装与调试原则，但是并未进行展开研究。文献[4]推导了磁传感器输出值的特征比值与弹体俯仰角的数学关系，研究了姿态角的解算与修正算法，没有进行实际实验验证。文献[5]从旋转体转速和地磁数据采样率两个方面进行了零点交叉法测量磁方位角的误差分析。文献[6]着重分析地磁场和传感器安装位置的空间关系，进行炮弹姿态角和磁方位角的推导和解算，解算误差为±0.4°。文献[7]采用非正交地磁传感器组合测量并计算得到地磁方位角和滚转角信息，解算误差为±0.2°。文献[8]提出了采用地磁传感器和光电传感器相结合的方法解算弹体的滚转姿态信息，解算角度误差在4°以内。本文针对使用陀螺仪对高速旋转弹体测姿误差大，存在漂移的问题，提出基于单轴磁传感器的旋转弹姿态解算算法。

1 旋转弹姿态解算原理

如图1所示，O-NED为地理坐标系，其中M为地磁场矢量，H为地磁场水平分量，d为地磁方位角，I为地磁倾角。O-xbybzb为弹体坐标系，是与弹体固连的动坐标系。O-xbybzb的原点O为弹体质心，Oxb为弹体对称轴，指向弹体头部；Oyb轴位于炮弹横截面内且垂直于Oxb轴；Ozb轴由Oxb轴和Oyb轴右手定则规定。弹体坐标系可以由地理坐标系经平移旋转变换而来，旋转过程的三个旋转角分别为偏航角ψ、俯仰角θ、滚转角φ。

图1 地理坐标系和弹体坐标系Fig.1 Geographical coordinate system and projectile coordinate system

由图1所示坐标系O-NED和O-xbybzb的关系，弹体旋转滚转角φ为0时，设这时与O-xbybzb重合的坐标系为准弹体坐标系O-xByBzB，准弹体坐标系可以由地理坐标系平移后经偏航角ψ和俯仰角θ旋转而来。此时地磁场矢量M和准弹体坐标系O-xByBzB以及弹体坐标系O-xbybzb的空间关系如图2所示。其中MxByB是M在xBOyB平面的投影，γ为M与xBOyB平面的夹角，α为投影MxByB与OxB轴的夹角。在弹体上安装磁传感器，在弹体旋转初始状态即φ为0时，传感器敏感轴OS在xBOzB平面内且与OxB轴的夹角为β，称为传感器安装角。

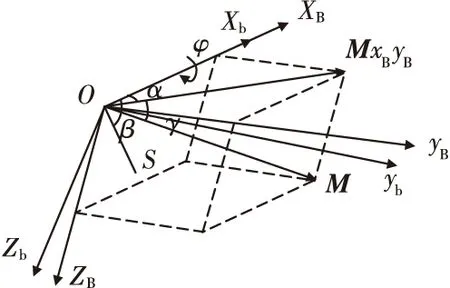
图2 弹体坐标系、准弹体坐标系和地磁场空间关系Fig.2 The spatial relationship of projectile body coordinate system, quasi-projectile coordinate system and geomagnetic field

在弹体飞行过程中，由于旋转角速度远大于偏航角和俯仰角变化率，因此假设在弹体飞行过程中，弹体旋转一周，γ和α不变，则磁敏感轴OS上的地磁强度变化和传感器安装角β及滚转角φ有关。在安装角度β已经固定的情况下，弹体旋转一周的OS轴地磁强度随φ变化。

由图1、图2所定义的坐标系和传感器OS轴以及相互之间的位置关系，可以求得传感器敏感轴上的地磁强度为：

MOS=MxBcosβ-MyBsinβsinφ+MzBsinβcosφ

(1)

式(1)中，MxB=Mcosγcosα，MyB=Mcosγsinα，MzB=Msinγ。

当β=0°或180°，即OS与Oxb轴重合时，有MOS=±Mxb=±Mcosγcosα，故弹体旋转一周，磁传感器输出的信号为一个大小和γ、α有关的常数，没有零点。

当β=90°，即OS⊥Oxb轴时，有：

MOS=-Mcosγsinαsinφ+Msinγcosφ

(2)

当γ=0°或180°且α=0°或180°，即M与Oxb重合时，MOS=0，MOS不随φ的变化而变化，弹体旋转一周传感器敏感轴上磁场强度皆为0；当γ=0°或180°且α≠0°或180°时，MOS=±Msinαcosφ，弹体旋转一周传感器敏感轴上磁场强度随φ呈正弦变化，幅值和α有关；当γ≠0°或180°且α=0°或180°时，即M在xbOzb平面内时，MOS=Msinγcosφ弹体旋转一周传感器敏感轴上磁场强度随φ呈余弦变化，幅值和γ有关；当γ≠0°或180°且α≠0°或180°时，有：

MOS=Asin(φ+φ0)

(3)

式(3)中，

弹体旋转一周传感器敏感轴上磁场强度随φ呈幅值为A，初始相位角为φ0的正弦变化。故当磁传感器安装角度与弹轴成90°且当地磁场方向不与弹轴方向重合时，弹体旋转一周，磁传感器输出的信号总有零点，但是零点的相位差不变且为90°。

当β≠90°，0°或180°时，有：

MOS=A0+Asin(φ+φ0)

(4)

式(4)中，

令Mos=0，可以解得：

(5)

式(5)在一个2π周期内有两解的必要条件为：

(6)

故当传感器安装角度不与弹轴垂直或重合，且满足式(6)要求时，传感器输出信号在一个弧度为2π的旋转周期内存在两个零点φs1、φs2，这时相位差为：

Δφs=φs2-φs1

(7)

从式(5)及式(7)可以看出，Δφs与γ、α、β有关，即存在函数关系f：

Δφs=f(γ,α,β)

(8)

式(8)数值解可由式(5)、(7)解出，f为用数值解拟合的函数关系。如果已知γ、α、β其中的两个量，由Δφs可以求出第三个量。

实际上，γ和α是未知的。对于弹体姿态常用欧拉角描述，即前文提到的偏航角ψ、俯仰角θ、滚转角φ。在当地地磁环境参数M、D、I已知的情况下，φ为0°时弹体三轴上的磁强强度为：

将上式代入式(1)可以得到与前述相似的结论。即对于高速旋转弹，解出φs′：

(9)

式(9)中，

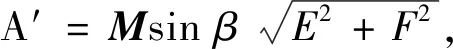
令：

(10)

则在满足|H|<1以及M、D、I不变的情况下，存在Δφs′：

Δφs′=φs2′-φs1′

(11)

从式(11)和式(9)可以看出，Δφs′与ψ、θ、β有关，即存在函数关系h：

Δφs′=h(ψ,θ,β)

(12)

若满足|H|<1，则θ和Δφs′、ψ、β之间存在唯一函数关系g：

θ=g(Δφs′,ψ,β)

(13)

将式(13)中的ψ、β视作常数，则可以通过式(12)解出数值解Δφs′，利用Δφs′和求解数值解Δφs′过程中使用的θ数据，拟合出函数g。

2 旋转弹姿态解算算法

2.1 假设条件

目前国内外主流火炮多采用线膛炮管设计，打出的炮弹都是旋转弹[9]。旋转弹的旋转速度较高，且在旋转一周的过程中，弹体滚转角的变化远远大于偏航角和俯仰角的变化。火炮射击射程较近，例如制式155 mm榴弹射程在60 km以内，可以忽略在该射程内地磁场强度矢量的变化[10]。

基于以上情况，提出以下假设条件：整个弹道过程中，偏航角ψ保持不变；弹体旋转一周过程中，旋转角速度是个常数且俯仰角不变；整个弹道过程中，地磁场强度矢量不变。

2.2 姿态角和地磁零点相位差Δφs拟合

基于地磁信号零点相位差计算姿态的原理，根据当地地磁环境参数，由火炮发射初始诸元，计算磁传感器在不同安装角度下旋转弹姿态角随地磁信号零点相位差的关系。

某地地磁环境参数D=-10.64°，I=65.9°，M=56 868.1 nT，由试验场炮位已知发射方位角可以确定ψ=148.62°。根据前述章节，可以求出：不同安装角度β，初始相位角φ0′和俯仰角θ的关系如图3所示；H和俯仰角θ的关系如图4所示；Δφs和俯仰角θ的关系如图5所示。

图3 不同安装角度β下φ0′随θ变化曲线Fig.3 Variation curve of φ0 with θ at different installation angle β

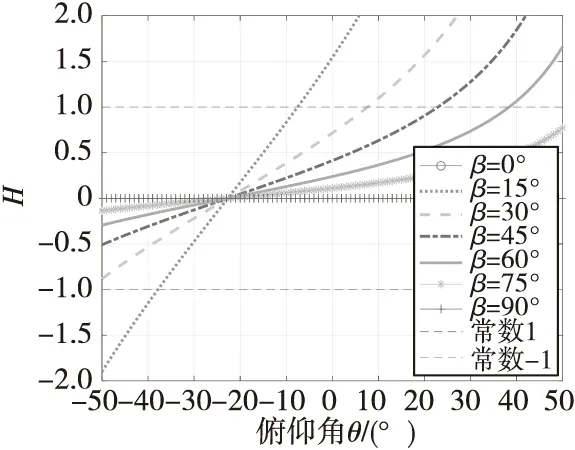
图4 不同安装角度β下H随θ变化曲线Fig.4 Variation curve of E with θ at different installation angle β

图5 不同安装角度β下Δφs随θ变化曲线Fig.5 Variation curve of Δφs with θ at different installation angle β

由图3可知，不同安装角度，旋转弹上磁传感器输出的地磁信号初始相位随俯仰角θ变化曲线重合，地磁信号初始相位和安装角度β无关。

从图4、图5可以看出，Δφs和俯仰角θ的关系在一定区域内是单调变化的，也就是说，利用零点相位差Δφs求解弹体姿态存在盲区。明显看出图4中H值落在(-1,1)之间时，图5中Δφs和俯仰角θ有确定的关系，此时对应的θ范围为姿态可求解区域。

图6所示是β=60°时θ随Δφs变化曲线。从图6可知，只要知道旋转弹弹体在旋转一周内的地磁信号的两个零点之间的相位差Δφs，就能求得在这个旋转周期内的姿态角θ。

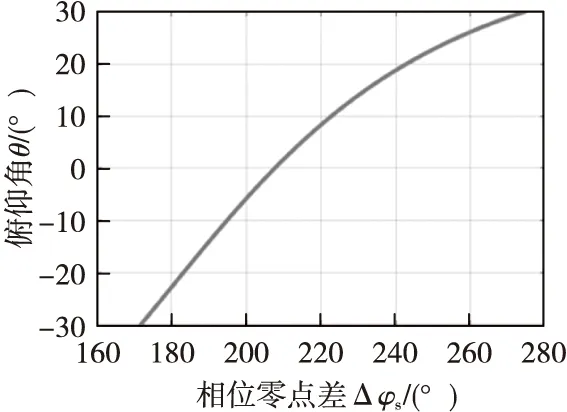
图6 β=60°时θ随Δφs变化曲线Fig.6 Variation curve of θ with Δφs at β=60°

2.3 安装角度β修正

实际工程中，地磁信号测试装置中的地磁传感器理论上应与弹轴成β角安装，实际安装的角度为β′，如果不进行安装角度修正，还以β角进行计算，则会形成误差。假设弹体的俯仰角θ=15°，理论安装角β=60°，未进行安装角β修正的情况下，真实安装角β′和俯仰角θ解算误差的变化关系曲线如图7所示。

图7 θ=15°，β=60°时β′随θ解算误差变化曲线Fig.7 Variation curve of β′ with the solution error of θ at θ=15°, β=60°

由图7可知，真实安装角β′和俯仰角θ解算误差变化关系是有规律的，当真实角度在60°±10°变化时θ解算误差在(-12°,11°)之间变化。安装角度误差的存在，将大大增加俯仰角θ的解算误差，所以需要对传感器安装角度进行修正。

安装角度的修正，是通过转台试验实现，转台的俯仰角是某一固定值，通过提取在转台上匀速转动一周的地磁信号，利用地磁信号零点信息求解俯仰角与转台俯仰角之间的误差，进一步根据真实安装角β′和俯仰角θ解算误差变化关系确定真实传感器真实安装角β′。

2.4 地磁信号处理

地磁信号经过信号去噪处理后，其零点提取流程如图8所示。

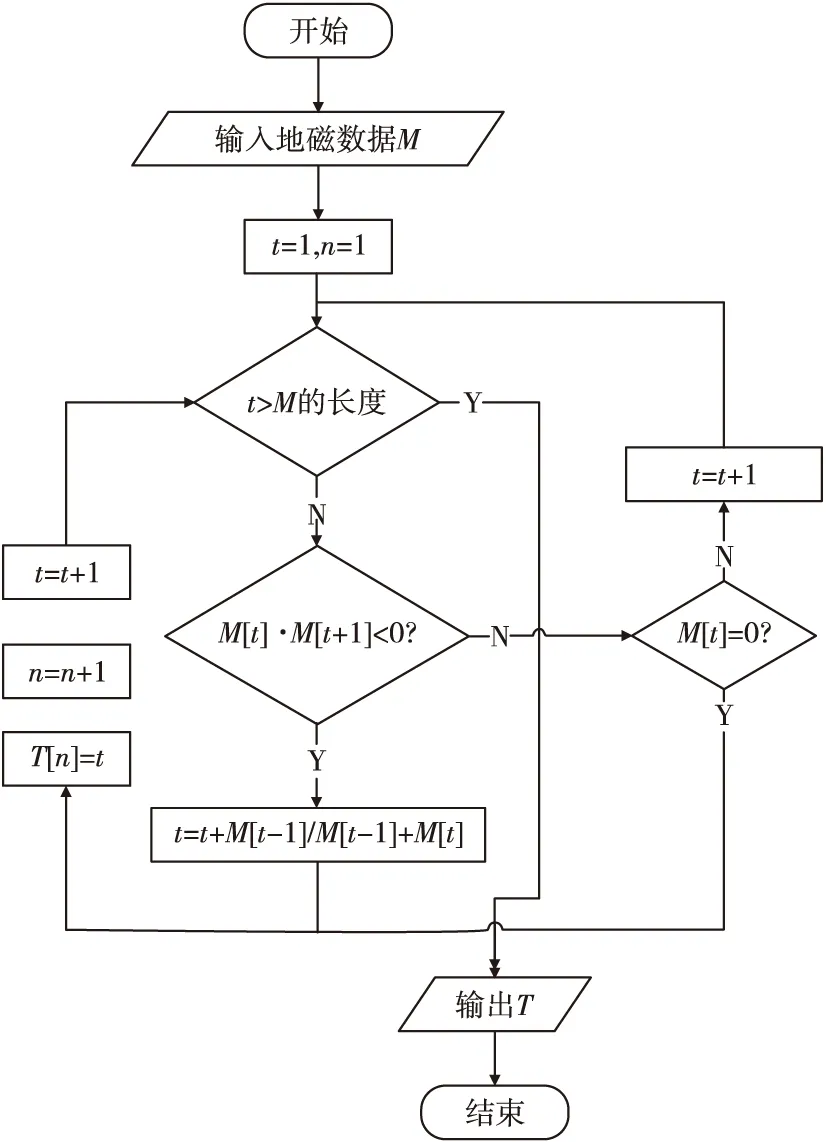
图8 地磁信号零点提取流程图Fig.8 Flow chart of zero point extraction of geomagnetic signal

T包含了弹体整个弹道过程中地磁数据的零点信息，提取出来的地磁信号时间零点T数据用于求解弹体每个旋转周期内的零点相位差Δφs，根据之前的假设，有：

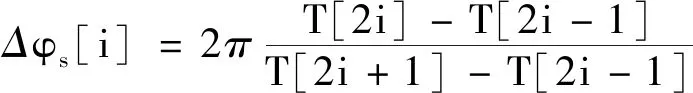
(14)

式(14)中，N是T数据的长度，Δφs包含了弹体整个弹道过程中每个旋转周期内的地磁数据零点相位差信息。

2.5 姿态角解算

由前文假设的条件，弹体每个旋转周期转速一定，只要求得每个旋转周期的角速度，就能求出滚转角。每个旋转周期的转速为：

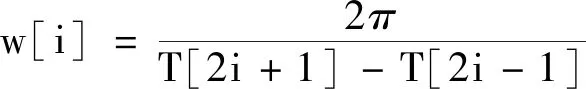
(15)

式(15)中，w包含了个旋转周期的旋转角速度信息。则滚转角为：

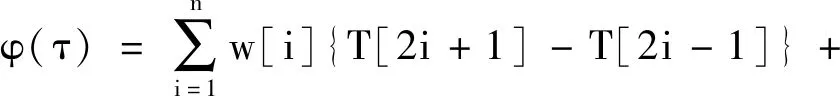
(16)

式(16)中，φ(τ)为某τ时刻弹体的旋转弹滚转角度值，n为时间T[2i+1]内弹体的旋转周数。

求解俯仰角θ，由修正后的安装角β′重新拟合姿态角和相位零点差Δφs的关系：

θ=g(Δφs,β′,ψ)

(17)

式(17)中，依据姿态解算假设条件，ψ=ψ0，是由已知条件发射方位角确定的。β′是修正后的安装角。将由式(14)求出的Δφs数据代入式(17)，可以求出：

θ[m]=g(Δφs[m],β′,ψ0)

(18)

式(18)中，θ[m]为弹体第m个旋转周期的俯仰角，Δφs[m]为弹体第m个旋转周期的地磁信息零点相位差。

3 火炮射击实验验证

为获取真实弹道地磁环境数据，本文进行了火炮射击实验，将地磁传感器沿弹轴方向和与弹轴成60°方向安装，对真实弹道环境地磁数据进行存储测试。火炮射击实验选取的研究对象为155 mm牵引式加榴炮杀伤爆破砂弹，发射药使用4号装药。实验过程中使用DR582弹道雷达跟踪弹丸位置，如图9所示，以获得弹道倾角信息。

图9 DR582雷达Fig.9 DR582 radar

实验中，存在磁干扰和测量噪声，磁干扰主要为铁磁干扰，设计磁阻传感器置复位电路和使用非铁磁性材料取代铁磁性材料减少铁磁干扰；对地磁数据使用小波变换进行去噪处理减小测量误差[11]。

存储测试系统所选地磁传感器为Honeywell公司HMC150x系列磁阻传感器，该系列传感器具有尺寸小、频响高、精度高等优点。传感器安装于榴弹引信结构中，存储测试装置如图9所示。

图10 存储测试装置Fig.10 Storage test device

3.1 实验初始参数

实验场地主要地磁参数如表1所示。

表1 实验场地地磁参数Tab.1 Geomagnetic parameters of test site

火炮射击试验主要参数如表2所示。

表2 火炮射击实验初始诸元Tab.2 Initial elements of artillery firing test

3.2 传感器测试数据

经过火炮射击实验，测得的弹轴方向和与弹轴成60°方向的地磁数据信息，经过信号处理后分别如图11和图12所示。图13为60°方向地磁数据局部放大图。

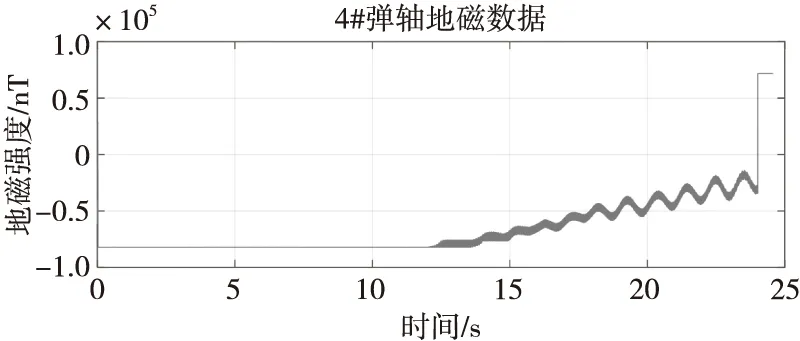
图11 弹轴方向地磁数据Fig.11 Geomagnetic data at projectile axis direction

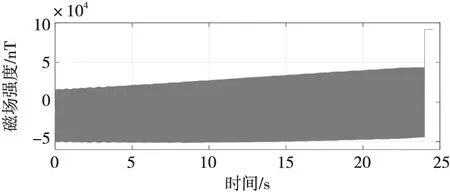
图12 60°方向地磁数据Fig.12 Geomagnetic data in 60° direction

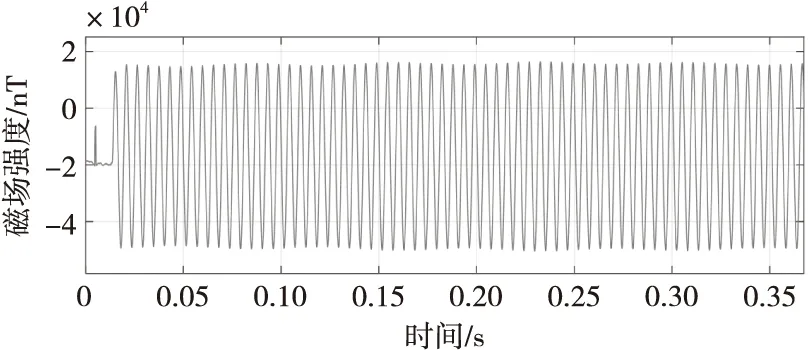
图13 60°方向地磁数据局部放大Fig.13 Partial enlargement of geomagnetic data in 60° direction

从图11可知，实验测得的弹轴方向地磁数据不完整，这是测试系统中弹轴方向磁传感器信号调理电路设计不合理造成的。从图12、图13可知，60°轴地磁传感器大概在20 ms开始有数据，说明存储测试装置在触发后经过20 ms左右飞出炮膛。60°轴地磁传感器数据较为理想，和理论推导几乎一致，该数据可以用来解算弹体姿态。

3.3 姿态解算结果

假设弹丸刚飞出瞬间滚转角为0°，则弹体旋转滚转角解算结果如图14所示。利用地磁数据解算的俯仰角值和实验中使用雷达弹道数据计算的俯仰角作对比，如图15、图16所示，俯仰角θ解算误差随时间变化曲线如图18所示。

图14 滚转角φ解算结果Fig.14 Rolling angle φ solution result

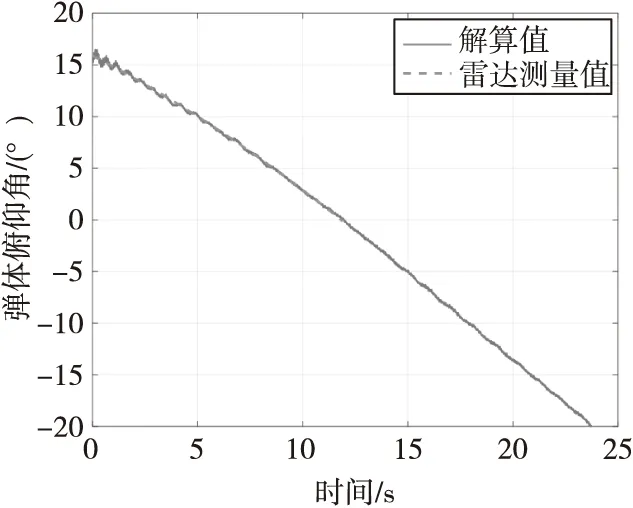
图15 俯仰角θ雷达数据和解算值Fig.15 Radar data and calculated value of pitch angle θ

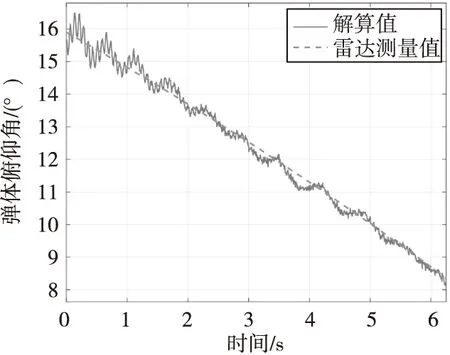
图16 俯仰角θ雷达数据和解算值局部放大Fig.16 Partial enlargement of pitch angle θ radar data and solution value

从图14滚转角φ解算结果可以看出，4号装药的155 mm榴弹在飞行过程中的旋转速度较高，旋转周期最快约为5 ms。从图15、图16俯仰角的解算结果可以看出，俯仰角变化率远远小于滚转角变化率，这也符合了前文提出的姿态解算假设条件。

从图16可以看出，解算出的俯仰角在某条曲线附近摆动，摆动频率由快慢两种频率组成。这是因为在弹体实际飞行过程中存在章动运动，其在弹道初始段表现最为明显，章动运动是一种二圆运动，势必会引起偏航角和俯仰角会有两种频率的微小摆动。为了和雷达数据比较，取俯仰角的解算值摆动中心，将俯仰角解算值摆动中心和雷达数据作比较，结果如图17、图18所示。

从图17姿态解算中心值与雷达数据对比和图18的姿态解算误差可看出，由于弹丸的章动运动，解算的弹丸俯仰角的最大误差出现在弹道的初始段，这个时候弹丸刚飞出炮膛，章动较大。通过本文提出的姿态解算算法解算出的弹道初始段俯仰角解算误差变化在0.15°以内，具备较高的解算精度。

图17 俯仰角θ雷达数据和解算中心值局部放大Fig.17 Partial enlargement of pitch angle θ lradar data and solution center value

4 结论

本文提出基于单轴磁传感器的旋转弹姿态解算算法。该算法同传统的地磁匹配算法相比，仅需一个磁传感器的地磁数据，且可显著降低地磁数据采集分辨率的要求，提升工程适用性。算法通过对磁传感器安装角的修正，提高了姿态解算精度。炮射试验验证结果表明，解算误差最大不超过0.15°，姿态解算误差较小，精度有所提高，具有一定的工程应用价值。