非合作辐射源雷达杂波建模方法

闫宇嘉，吉琳娜，宋 杰，杨风暴

(1.中北大学，山西 太原 030051；2.中国人民解放军海军航空大学，山东 烟台 264001)

0 引言

随着雷达技术的迅速发展，研究人员已经不再满足于对简单目标的处理，而转向高杂波环境、特殊目标以及区域范围动态化处理等方向。双基地雷达由于收发系统分置，基于此提出了非合作运动辐射源雷达系统[1-3]，该系统发射装置为预警机，接收站可配置高精度雷达，通过固定的接收系统接收直达波参考信号和目标回波，实现对目标的探测与定位，不仅继承了双基雷达的“四抗”优势，也可用敌方雷达检测敌方目标，优势十分明显[4-6]。

双基地机载预警雷达已受到研究人员的关注。1995年，R.Klemm[7]在采集MCARM数据时，专门有四次飞行是用于采集双基地机载预警雷达数据的，他从杂波多普勒频率及杂波散射体与接收机、发射机之间的双程距离关系出发，建立杂波模型；但该模型所产生的杂波协方差矩阵是不适合作自适应处理的，因为发射方向图对杂波特性的调制很难在杂波抑制中得到补偿和抑制。海军航空大学于2014年，研究了海上非合作雷达源的信号特征、天线扫描调制影响、直达波脉冲丢失与相位突变影响，以及双基地海杂波抑制等问题[8]。文献[9—11]建立了地心直角坐标系，模型以接收机、发射机、地心三者所在的平面建立坐标系。以上模型接收机都属于运动状态，当接收站处于固定状态，装载精度足够的雷达，运用非合作运动雷达辐射源提供雷达信号，可以为目标检测提供新的思路。

基于此，本文针对双基地雷达辐射源、接收站与地物杂波存在相对运动，导致雷达配置场景下出现的杂波复杂化问题，借鉴文献中杂波数据的仿真方法，简化了几何模型，提出非合作辐射源雷达建模方法, 并基于该方法，对空时二维杂波特性进行了分析。

1 非合作辐射源雷达杂波系统的应用场景和几何关系

非合作辐射源雷达系统应用背景如图1所示。杂波的建模思想，便是以接收站和辐射源所在的坐标为核心，根据辐射源所辐射的电磁波对目标进行处理，然后将系统所引起的杂波变化进行处理，由于杂波在一定程度的大环境下属于相对静止，则杂波的空-时-频域中的空-频域关系便可以决定杂波的二维谱分布特点。

图1应用背景Fig.1 The application background

根据研究背景建立数学模型如图2所示。R为接收站，T为辐射源，P为杂波环上的杂波点。依据假设可知，辐射源是匀速运动的，信号产生即为通过辐射源T，然后经过杂波点P后传输给接收站R。并且接收站可分为直达波通道和回波通道，为了体现杂波特性，此次杂波模型并不考虑辐射源T本身对接收站R的影响。

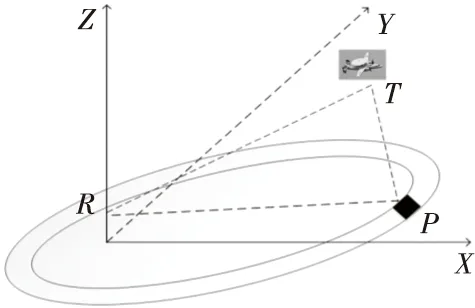
图2 杂波环几何分布Fig.2 Clutter rings are geometrically distributed

2 非合作辐射源雷达杂波建模方法

为了简化模型的复杂程度，作以下假设环境条件：1)电磁波在标准大气压状态下进行传播；2)地面粗糙不平的部分远小于辐射源与地物的距离；3)外辐射源在空中作水平运动；4)在几何坐标内，杂波处于平稳状态。

2.1 杂波几何模型

根据以上假设条件建立的位置几何模型如图3所示。

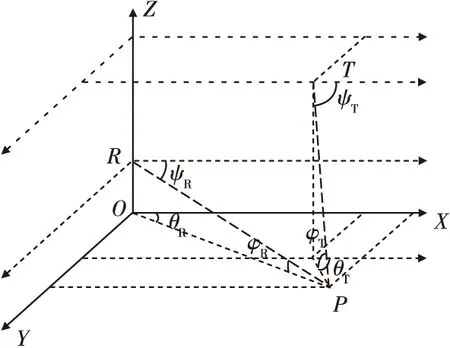
图3 杂波相对于应用背景的几何模型Fig.3 Geometrical model of clutter relative to the applied background

设辐射源与接收站的位置分别为T(xT,yT,zT)、R(xR,yR,zR)，并且设置杂波点P的位置为(xP,yP,0)。由于接收站是位于z轴的，所以接收站的坐标简化为R(0,0,zR)。电磁波从T出发，经过P点最后被接收站R所接收。图中θT,θR分别为杂波相对于辐射源和接收机的方位角；φR,φT分别为杂波相对于辐射源和接收站高低角；ψT,ψR分别为杂波相对于辐射源和接收站的杂波入射锥角。设辐射源的运动状态可以随意改变，位置也可以随机改变，它们的天线均为M行N列的矩形侧面阵列，阵元在行与列方向均为等间隔。

由于接收站的位置固定，数学的模型可以简化。由辐射源所发射的信号经过P点到双基地距离之和设置为l，即RTP+RRP并且设置辐射源的速度为V(xV,yV,zV)，则地面的等距离曲线方程为：

(1)

则等多普勒曲线满足以下方程：

(2)

由于参数的设置，我们对于杂波点P的坐标未知，可以根据图2了解到P的点可以围成杂波环，根据式(1)可得到等距离曲线方程，由于未知的参数很多，对隐函数求解困难，所以我们将其改成参数方程[10]，根据以上公式以及接收站的坐标简化为R(0,0,zR)，并且设P点的坐标可用参数坐标(ρcosφ,ρsinφ)表示，则可以得到以下方程：

(3)

未知量随之改变，则多普勒曲线可得：

(4)

(5)

又因为zR≪ρ，所以简化上式可以得到ρ有：

(6)

这个公式表示参数方程内杂波点到坐标原点的距离。

2.2 基于天线增益杂波模型

散射单元的具体表达式可用Pi(n,k)表示，理想情况下第n路(列子阵)的第k个脉冲对第i个杂波距离环的采样数据，公式如下：

(7)

式(7)中，k表示子阵的第k个脉冲接收到的信号；RTPRRP表示双基地与杂波点的距离之积；gTP(θT)gRP(θR)表示发射天线增益和接收天线增益[12]。则发射机和接收站的接收增益可以用以下公式表示：

(8)

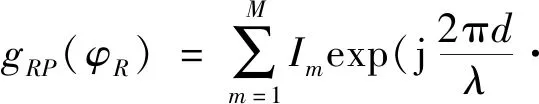
(9)

式(8)、式(9)中，Im、In分别为固定的列、行子阵加权。

ws和wt分别是空域角频率和时域角频率，由于只是接收站进行数据处理，并根据杂波P的参数表达式，亦可将俯仰角进行改变，则可得出公式(10)。

式(10)中的fr是脉冲重复频率。将式(8)—式(10)带入式(7)中，即可得到所需杂波的数据，并且设置在观测的时间内接收到k个脉冲，用NM×1维矢量P=[P11,P12…,PN1,…，P1M,P2M，…,PNM]表示空时二维杂波样本，N为接收天线的阵元数，M表示相干脉冲个数。设PKL为第K个阵元第L个脉冲信号，则RP=[PPH]表示杂波的二维协方差矩阵，则RP的矩阵元素为式(11)所表示。

(10)

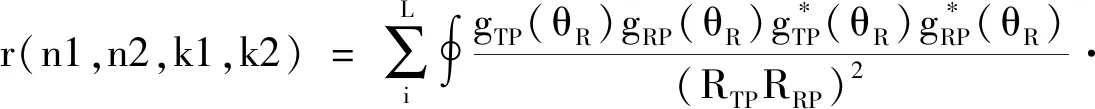
(11)

式(11)中，n1,n2=1,2，…，N;k1,k2=1,2，…，K，此处r表示假设不同距离单元的杂波回波信号互不相关。以上公式是根据雷达的接收站所接收的信号进行处理，将辐射源所引起的杂波变化映射到接收站上，进行建模。

定义Ss(ws)=[1,ejws(θ,φ),…，ej(N-1)ws(θ,φ)]与St(wt)=[1,ejwt(θ,φ),…，ej(N-1)wt(θ,φ)]T分别是空域导向矢量、时域导向矢量，则空时二维导向矢量定义为Ss(ws)和St(wt)的Kronecker积S(ws,wt)=Ss(ws)⊗St(wt)，所以对杂波协方差矩阵RP的变量[ws,wt]在相应的取值内遍历就可以得到二维杂波功率谱：

(12)

以上便是二维杂波功率谱，将分置的发射机所引起的杂波变化映射到接收站上。

3 仿真结果及杂波特性分析

3.1 参数设置

接收站的接收波束按正侧视阵配置，发射波束指向为阵列法线方向，其参数依据现有机载预警雷达的工作模式和工作参数范围等进行设置，具体参数如表1所示。

表1 非合作辐射源雷达参数Tab.1 Non-cooperative emitter radar parameters

3.2 数值仿真分析

根据表1的参数，设置非合作辐射源不同速度矢量的仿真结果如图4所示。

图4 杂波方位角与多普勒频率关系图Fig.4 Cluttered azimuth and Doppler frequency relation diagram

图4是根据式(4)得到的多普勒曲线。根据以上的四幅图，我们可以很清晰地看到，多普勒的变化会随着辐射源的速度而改变，并且速度的大小会影响多普勒频率的大小，方位角在0°～100°时多普勒值的变化率十分明显，其他范围则相对平缓，并且这种分布特点不会随着辐射源速度的改变而改变，说明主瓣的波束范围会导致杂波的展宽变大，而其他方位的杂波谱展宽较小。

当速度的取值由于方向的原因不同时，曲线虽然有着很明显的变化，但它们的趋势却是一致的，并且四幅图的趋势在某种程度上有着相似性。同时也可以得到，若是预警机的速度方向(发射阵列的方向)和接收站的接收方向(接收阵列方向)不同时，会导致多普勒变化出现偏差，会导致杂波谱的展宽有所变化。由此可见，仅仅对运动的辐射源进行简单的多普勒频移抑制杂波，可能达不到预期的效果。

而影响多普勒曲线效果是由预警机作为辐射源的相对速度导致的。针对速度不同而引起的杂波谱的变化，采用数值仿真来描述Ws与Wt的关系，并将相对速度的方向进行改变，速度方向分别为正/负径向、切向、斜向(夹角为30°)。

图5是Ws与Wt的关系图，当杂波环即杂波点到双基地距离和l的大小趋于很大时，Ws与Wt的关系趋于一致，接近重合，相反，在近距离情况下，它具有快速锐利的特点。

图5 辐射源速度矢量不同时的Ws与Wt曲线Fig.5 The Ws and Wt curves with different velocity vectors of the emitter

以上的图像没有进行距离模糊处理，只考虑了无距离模糊时单距离环杂波回波。由于其中没有考虑由于距离模糊引起的杂波叠加对杂波功率谱的影响，所以文中给出的杂波谱显得非常“规则”。但这是不符合机载雷达实际工作情况的，因为雷达在采用高、中脉冲重复频率工作时，必然存在距离模糊问题。在双基地雷达系统中，雷达最大不模糊距离由脉冲重复频率fr所决定，即Rsu=c/fr，其中c表示光速，并且需要对一个杂波单元进行全程距离模糊处理，以下仿真便是加入距离模糊后的结果。

当l值的大小趋于杂波环取值极限时，根据式(12)可得到图6的结果。

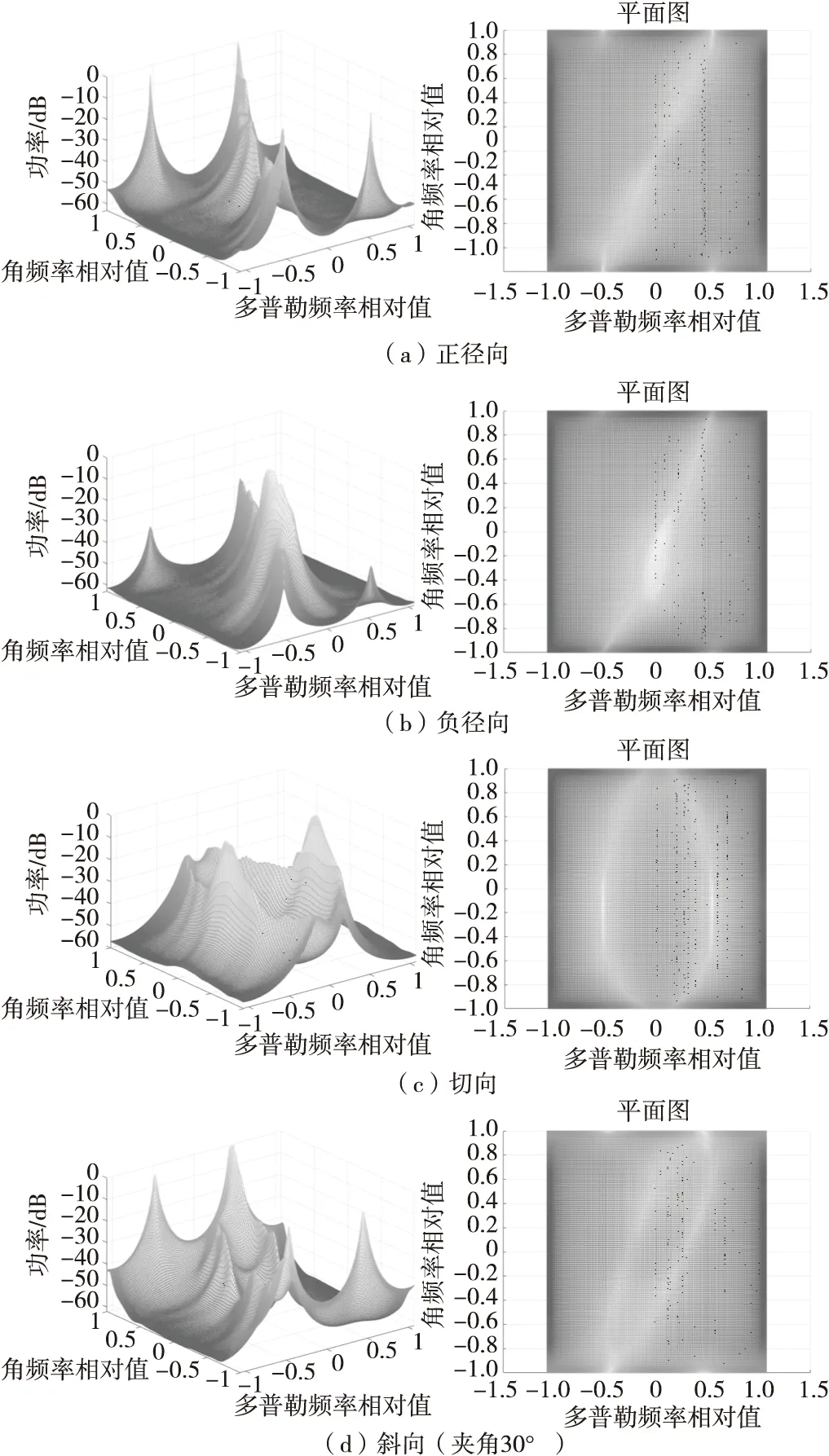
图6 辐射源速度矢量不同时的杂波谱Fig.6 The clutter spectrum of the emitter with different velocity vectors

通过平面图的杂波谱趋向，并与Ws与Wt的关系图对应，可以判定二维谱的正确性。

根据以上的四组实验可以得到，当辐射源处于正径向运动时，杂波分布的不一致性扩大，趋于两极化；而辐射源相对于接收站时负径向运动时，可以将其当作单站雷达，杂波的分布也趋向于单站雷达的波形；当辐射源切向运动时，杂波多普勒曲线封闭，相互之间分散，并且相对于前两种配置，第三种配置距离相关性减弱；当辐射源速度与接收站接收方向呈30°夹角时，杂波谱的前后瓣不对称，且在距离增大时曲线封闭，杂波特性随着距离增大而逐渐减弱。

非合作辐射源雷达系统下的特征谱即根据矩阵R所求，图7为四种配置条件下的特征谱。由于特征值的大小与阵元相关，图中将其统一为正数，从图中可以看到特征谱的数目基本大于N+M-1，这和R.Klemm的结论一致，而且由于双基地和单基地的几何配置下自由度的不同，特征根的数目远大于N+M-1。根据特征根的自由度也可以得出，方向比较规整时杂波谱也趋于规则化，但当辐射源的速度角度和接收站方向呈任意角度以及趋于切向时，杂波的自由度会增大，意味着杂波谱的复杂程度也会加深。

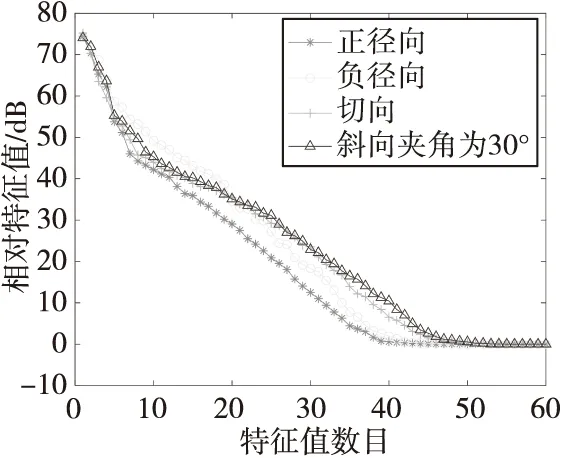
图7 杂波协方差矩阵的特征值Fig.7 The eigenvalues of the clutter covariance matrix

4 结论

本文提出非合作辐射源雷达杂波建模方法。该方法构建了非合作运动雷达辐射源及固定地面接收站体制下的双基雷达构型，对其杂波分布的影响进行了理论分析和仿真研究，验证了该杂波模型的有效性，根据仿真结果评估其杂波特性。仿真结果表明：双基距离和单元在大地固定坐标系水平面内成椭圆，验证了模型的正确性; 通过分析不同辐射源速度情况下的接收站所得到的杂波特性，研究杂波特性分布的距离依赖性，并得到不同配置下，杂波点到双基距离越小，杂波的变化率越大，相关性越强，随着距离增大，杂波特性对于距离的依赖减弱；并且辐射源速度与接收站的接收方向有着密切关联，二者的角度越趋于复杂，自由度会随之增大，它们的杂波谱也会趋于复杂。本文提出的二维杂波谱建模方法适用范围得到了扩展，简化了计算，为非合作运动辐射源雷达系统的杂波抑制、目标检测奠定了基础。