基于ICA-TOPSIS法的空战威胁评估

彭明毓，李战武，杨爱武，奚之飞，方诚喆

(空军工程大学航空工程学院，陕西 西安 710038)

0 引言

近些年来，空战的对抗模式伴随着智能化、信息化的发展而发展，尤其是新一代前沿技术的应用研究使得飞行员所面临的空情愈加复杂，同时在电磁环境的影响下，飞行员所能获得的空战目标状态信息也愈加不充分。当下，信息“无所不至”的空战场中，空战对抗逐渐向“瞬时对抗”转变，进而要求对抗短时且高效。而把握空战的态势进行实时、准确的空战威胁评估，则是战机夺取空战先机的关键。因而，信息化条件下，空战威胁评估在对抗中的地位愈加凸显。

威胁评估是空战对抗中的一个重要环节，吸引着众多学者进行深入研究。目前，常见的空战威胁评估方法主要分为两类：一类是基于参量模型的方法[1-3]，主要思想是通过完善目标态势评估的推理模型，同时可利用智能算法进一步优化，最终实现对目标威胁的评估，但此类方法对先验知识和参数的要求均较高，导致实时性不高；另一类是基于非参量模型的方法[4-7]，主要思想是通过目标态势评估模型或评估指标权重选取的优化与改进，进而实现客观威胁评估，此类方法较为简单且易实现，并通过优化权重，一定程度上能满足主客观性的要求。文献[4]最先将TOPSIS法引入至空战中，实现对空战威胁的客观评估，但缺乏专家主观知识经验支撑；文献[5]通过引入层次分析法构建组合赋权优化权重模型，对空战威胁进行主客观评估，但未考虑空战中的复杂耦合环境，即采用TOPSIS法的前提无法满足；文献[6]引入粗糙集优化权重以降低主观性和先验知识需求的影响，但仍无法满足TOPSIS的前提。以上文献均未考虑复杂耦合指标下的空战环境。文献[7]则针对耦合指标问题，提出灰色关联度模型修正耦合指标权重，实现耦合指标下的威胁评估，但仍难以解决耦合指标对TOPSIS理想解偏差的影响。上述文献均仅从优化权重进行分析考虑，未能从根本上解决指标耦合问题而存在结果偏差。

本文针对传统空战威胁评估方法存在的问题，提出基于ICA-TOPSIS的空战威胁评估方法。通过引入独立成分分析方法，采用FastICA算法对干扰耦合的空战目标状态数据进行分析，以解决耦合的空战指标下导致的威胁度偏差问题。仿真实验验证了方法的可行性。

1 独立成分分析与逼近理想解排序法

1.1 盲源分离——独立成分分析法

盲源分离(BBS)是指观测到一组相混合的信号，通过分离技术得到无法被直接观测的各个源信号独立成分。其运用的思想可以归纳为：寻找一个线性表示，使得该表示所对应的成分是统计独立的。关于盲源分离问题，大部分采用独立成分分析(ICA)的方法。

独立成分分析法是从多维统计数据中得到潜在因子或成分的分析方法[8]，最初为利用代数和高斯统计量实现的方法[9-10]，后续演化为一种综合利用统计、信息论、神经网络和优化方法等多门学科的新兴信号处理方法。而在空战的实际对抗过程中，目标状态信息的获取也正是通过信息的传递与分析得到的，而混合(如与干扰信息混合)的目标不同状态信息分离则可通过ICA技术进行实现。如图1所示，假设有一组无法直接通过观测得到的信号源 ，进行如(1)所示的线性混合过程：

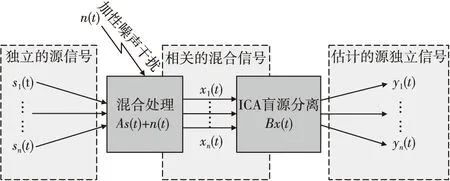
图1 信号的混合与分离过程Fig.1 The process of signals mixing and separating

x(k)=As(k)+n(k)

(1)

式(1)中，A∈M×N为未知混合矩阵，x(k)为信号源混合得到的信号集合(可直接被观测)，n(k)=[n1(k),n2(k),…,nm(k)]为加性高斯白噪声，即干扰信号。由于信号经过混合与干扰，所被观测的信号x(k)相对于源信号s(k)是相互耦合关联的。

为获得源数据的估计，引入分离矩阵B∈M×N。通过不断调整分离矩阵B来得到一组估计值y(k)=[y1(k),y2(k),…,yn(k)]，且y(k)由式(2)得到：

y(k)=Bs(k)

(2)

盲源分离的目的就是使得估计得到的y(k)尽可能的接近源数据s(k)。因此，分离矩阵B必须收敛于混合矩阵A的逆矩阵。由于数学上的限制，BBS方法中还固有次序模糊和尺度模糊[11]。这是因为，该方法中各个分量之间的排序以及尺度缩放是允许不尽相同的。因此，在本文的算法中，需要处理这些模糊以避免造成结果上的偏差。

在独立成分分析法中，有两种算法可用来处理多属性决策问题。一个算法是由Cardoso等人于1993年提出的联合逼近对角化特征矩阵(JADE)算法[12]。该算法利用信号的自身特征，通过计算高斯累积量将盲源分离问题转化为特殊矩阵的对角化问题，最终得到源信号的独立性。JADE算法由于通过矩阵的特征分解和联合对角化计算进行独立性估计，导致存贮空间大，因此，尽管JADE算法有着解决独立性一致的源信号进行信息分离问题的优势，即估计更加准确，但不适宜直接用于多维度指标的空战威胁评估当中。

另一个是由芬兰学者Aapo Hyvarinen等人于1997年提出的FastICA算法[13]。该算法使用峭度或者负熵来作为非高斯性度量，用以度量独立性。其中，峭度定义为一个随机变量的四阶累计量：

kurt(y)=E{y4}-3(E{y2})

(3)

通过峭度来判定变量间的独立性，最后通过峭度最大化以估计得到每个源信号。FastICA将直接度量的独立性间接转化为非高斯性的度量，通过寻求基于独立性最大化的目标函数，采用不动点迭代算法对目标函数进行优化，得到解混合矩阵的最佳估计以实现混合信号的分离。基于FastICA的分离算法能够快速的收敛，且算法中没有学习速度或其他大量的需调参数，实时性较高，符合空战的实际特点。

在博弈性空战对抗过程中，实时获取目标真实状态信息是占据空战主动的关键。然而，战场环境的复杂性以及多机协同干扰掩护等导致载机获取的信息并不准确，因此，基于ICA的盲源分离技术，通过数据驱动，可进一步分析所获数据的潜在价值。在空战目标威胁评估当中，所获目标数据的耦合性将一定程度上造成评估的偏差，从而影响飞行员的决策。为获得准确的空战威胁态势评估，需要对所获得的目标数据进行解耦，而ICA技术正适用于该解耦问题。如图2所示，可引入信号分离处理的ICA技术对载机传感器所获得的数据加以解耦。同时，为实现较快的收敛效果和鲁棒性，本文采用了FastICA算法，对得到的目标独立威胁指标值进行分离估计。

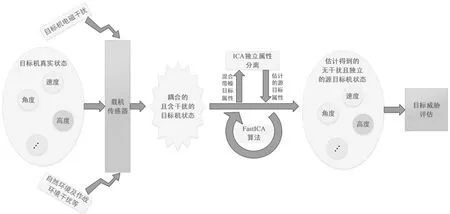
图2 基于ICA的目标状态信息解耦Fig.2 Targets state information decoupling based on ICA

1.2 方案优劣排序——逼近理想解法

传统的TOPSIS算法是基于计算方案与正负理想解之间的欧里几德距离[14]，从而将接近度最小的方案判定为最劣方案，反之为最优方案。同时，通过接近度大小可对备选方案进行优劣排序。限于篇幅，TOPSIS的计算流程及公式可参考文献[4]。

传统的TOPSIS可对独立属性下目标方案的优劣进行排序，然而在复杂环境的空战下，载机所获得的目标状态属性间将不再满足独立性的基本前提。此时，TOPSIS法所计算的欧式距离将包含冗余的信息，进而导致目标威胁度的偏差。因此，为去除冗余的信息，改进的TOPSIS-M法引入了二阶统计量——协方差，来考虑两个多维随机变量之间存在的相关性，即引入关联性度量Σ：

Σ=E{(U-E(U))(U-E(U))T}

(4)

式(4)中，U为已标准化的评估矩阵。同时，其采用马氏距离[15]来代替欧氏距离以度量每个方案与正负理想解之间的距离。马氏距离DM定义如下：

式(5)中，u为相同指标下不同的目标状态组成的列向量；u±为不同指标下的正负理想解[4]；Δ为指标对应权重ω构成的对角矩阵，即Δ=diag(ω1,ω2,…,ωM)；Σ为关联性度量，即协方差矩阵。

TOPSIS-M算法通过引入协方差矩阵消除了属性之间的关联性，并以马氏距离作为度量方式，但在确定正负理想解时，仍是以混合后的耦合数据确定的。因此，TOPSIS-M方法得不到针对原有的独立属性的准确目标理想解，最终可能导致所得到的距离仍离理想解较远。基于ICA-TOPSIS的方法就可解决这个理想解的偏差问题，同时，将耦合指标进行解耦分析，得到的独立属性更适合作为TOPSIS的输入。

2 基于ICA-TOPSIS的空战威胁评估

2.1 空战目标威胁评估指标体系建立

随着空战武器装备的集成与发展，先进战机的隐身、攻击、机动、干扰等性能不断地提升以及愈加复杂的作战环境，导致载机获取目标状态信息难度增大，进而产生空战威胁评估结果的偏差。空战威胁评估所涉及的指标众多[3]，因此，在进行相应的评估前，需要确定具有代表性且能够提供反映目标威胁信息的关键指标。综合考虑各项因素，仿真实验中主要分析目标的空间态势、空战能力以及作战意图指标，如图3所示。限于文章篇幅，各威胁指标具体的计算公式不再赘述，可参考文献[7，16—21]。

图3 空战威胁评估指标体系Fig.3 Threat assessment index system for air combat

本文所考虑的空战态势指标包含速度、隐身、角度、距离等4个威胁因子，通过空战目标的速度、角度、RCS、距离等信息代入文献[7，17—20]的威胁模型中即可得到；对目标的空战能力指标，文献[16]依据相对参数衡量作战飞机的能力，以现代战机先进指标或标准值为基准，采用幂数作为作战能力指数，且针对空战目标的机动性、火力、探测能力、操作效能、生存力、航程和电子对抗能力，采用对数法构建最终得到空战能力指数威胁因子；对目标作战意图指标，文献[21]通过给定不同的作战意图得分对应得到作战意图威胁因子。

2.2 ICA-TOPSIS法威胁评估

针对空战威胁指标属性间存在的关联性问题， ICA-TOPSIS方法通过独立性估计解决该问题，其威胁评估过程如图4所示。首先建立ICA估计模型以估计出所观测威胁属性的独立隐属性；接着对估计得到的数据进行处理，避免次序模糊和尺度模糊；最后将调整后的隐属性和权重作为TOPSIS的输入，利用TOPSIS法进一步得到目标威胁等级排序。

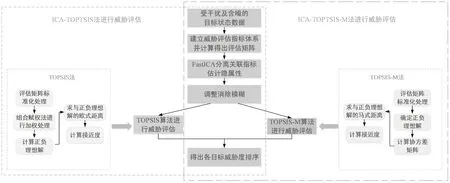
图4 空战威胁评估流程Fig.4 Air combat threat assessment process

具体的步骤如下：

4) 对威胁目标进行排序。通过计算得到的接近度γ，对目标的威胁度进行排序。

如图2所示，空战过程中，载机所想获取的目标的各个指标属性值s(t)是相互独立的，但由于传感器所接收的信号可能受到干扰或信号相互叠加，导致载机最终所能观测到的是相关联的属性x(t)。为能准确地进行TOPSIS威胁评估，采用ICA技术估计独立属性y(t)≈s(t)。

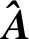
1) 置换

(6)

2) 反转

3 空战实例分析

3.1 空战对抗过程想定

假设我方战机在空域中遭遇敌方4架战机，分别为F-16C、F-15C、F-5G三种机型。在某一时刻，我方战机与目标线之间的夹角为20°，飞行速度为300 m/s，导弹的最大射程为80 km，雷达的最大作用距离为140 km，RCS为6 m2，门限RCS为2 m2。通过文献[16]中公式的计算，求得敌方4架3种机型战机的空战能力指数分别为16.8、14.4、13.4，其对应RCS分别为4.9、11.3、5.5，且所携带的空空导弹的最大作用距离为100、60和70 km，雷达最大作用距离为130、160、120 km。某一时刻各敌机的部分空战状态可参考文献[21]，如表1所示。

表1 敌机某一时刻的空战状态Tab.1 Air combat status of enemy at a certain moment

3.2 基于ICA-TOPSIS的各目标威胁度计算

根据3.1节的作战想定，代入威胁指标因子计算公式[7,16-21]，得到各目标威胁因子值，如表2所示。

表2 各目标的威胁因子值Tab.2 Threat factors value of each targets

由表2得到评估的决策矩阵V为：

通过层次分析法，可得到各指标的主观权重为：

WS=[0.394 5,0.051 7,0.079 9,
0.158 4,0.243 5,0.072 0]

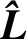
最后通过TOPSIS法，得到各目标的接近度为：

从而得到目标威胁的威胁度排序为：4>1>3>2。ICA-TOPSIS的结果与TOPSIS、TOPSIS-M的结果对比如表3所示。

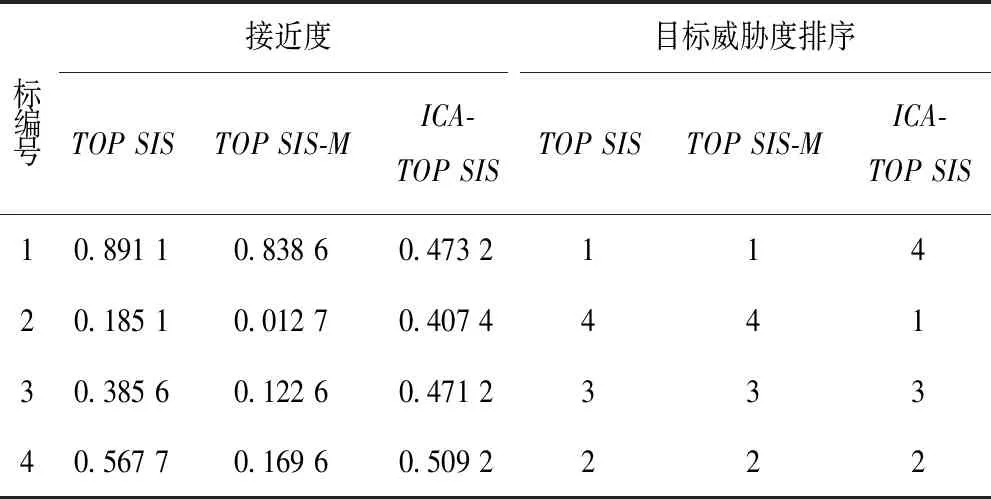
表3 各算法的威胁评估结果Tab.3 Evaluation results of each algorithm

如表3所示，本文提出算法得到的威胁结果排序与传统算法结果排序不一致。事实上，由于在获取信息耦合度较强的情况下，采用原耦合数据计算的威胁因子存在偏差较大，进而结果不一致。后续仿真中将进一步做干扰耦合下威胁度偏差分析。

4 仿真对比分析

通过第3章的实例分析，ICA技术用于空战目标威胁评估能够得出较合理的目标威胁等级排序。为进一步对该算法进行仿真验证，采用反向验证法，即在特定条件下一部分独立的威胁评估指标，通过某一关系进行耦合，得到耦合的威胁指标，再通过ICA技术进行相应的分离，验证其准确性，同时对比基于耦合性指标下TOPSIS法、TOPSIS-M法的威胁评估结果。

在忽略机身构造所造成的不同角度可能影响飞行速度，可认为角度因素和速度之间不存在耦合关系，即角度威胁和速度威胁两个评估指标可视为相互独立。同时，忽略因飞机的各器件故障因素造成某些性能的影响，如机动性能间接影响到飞机的角度和速度能力，而间接影响目标到速度威胁和角度威胁，即可认为空战能力威胁与角度威胁、速度威胁三个指标是相互独立的评估指标。为简便计算以及有效说明问题，本文仅选取以上指标进行相应的威胁评估，同时，选取25个不同时刻目标数据进行分析，对比其他算法在威胁评估中的结果。

4.1 目标数据的处理及权重、混合矩阵的确定

选取25个连续或不连续时间点目标的角度、速度值，计算相应的三个威胁评估指标值，并通过组合赋权法获得相应的权重。

此时，所得到的角度、速度、空战能力都是独立的，而实际观测到的数据往往是相互耦合关联的，因此，利用混合矩阵进行混合，生成相互耦合的数据。针对空战过程中，干扰对真实数据影响反映为目标状态值的偏差，因此，混合矩阵A可设为：

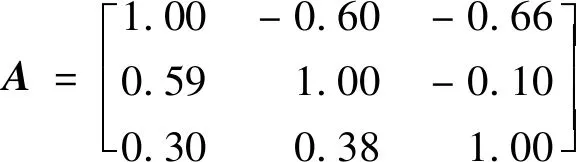
(7)

同时，在真实的对抗过程中，我方获得的数据往往受到敌方及电磁环境的干扰，即获得的数据含有噪声。因此，考虑不同的信噪比对评估的影响，信噪比定义如下：

(8)

4.2 算法对比分析

考虑到最初假定角度、速度及空战能力数据独立，因此，将得到的决策矩阵用作TOPSIS输入，其所得到的结果可认为是准确理想的，后续的对比将此结果视为真实理想的结果。仿真实验将通过混合矩阵A混合得到的决策矩阵作为TOPSIS、TOPSIS-M、ICA-TOPSIS输入，所得到的各结果利用评价指标与真实理想的排序结果进行对比分析。

在不同的干扰等级下，所获得的目标真实状态存在偏差，最终导致空战威胁因子的偏差。在仿真实验中，分析不同干扰等级下对目标威胁度的影响。进而分析，在不同干扰情况下，目标信息获取的偏差所导致目标威胁评估的偏差程度，如表4所示。

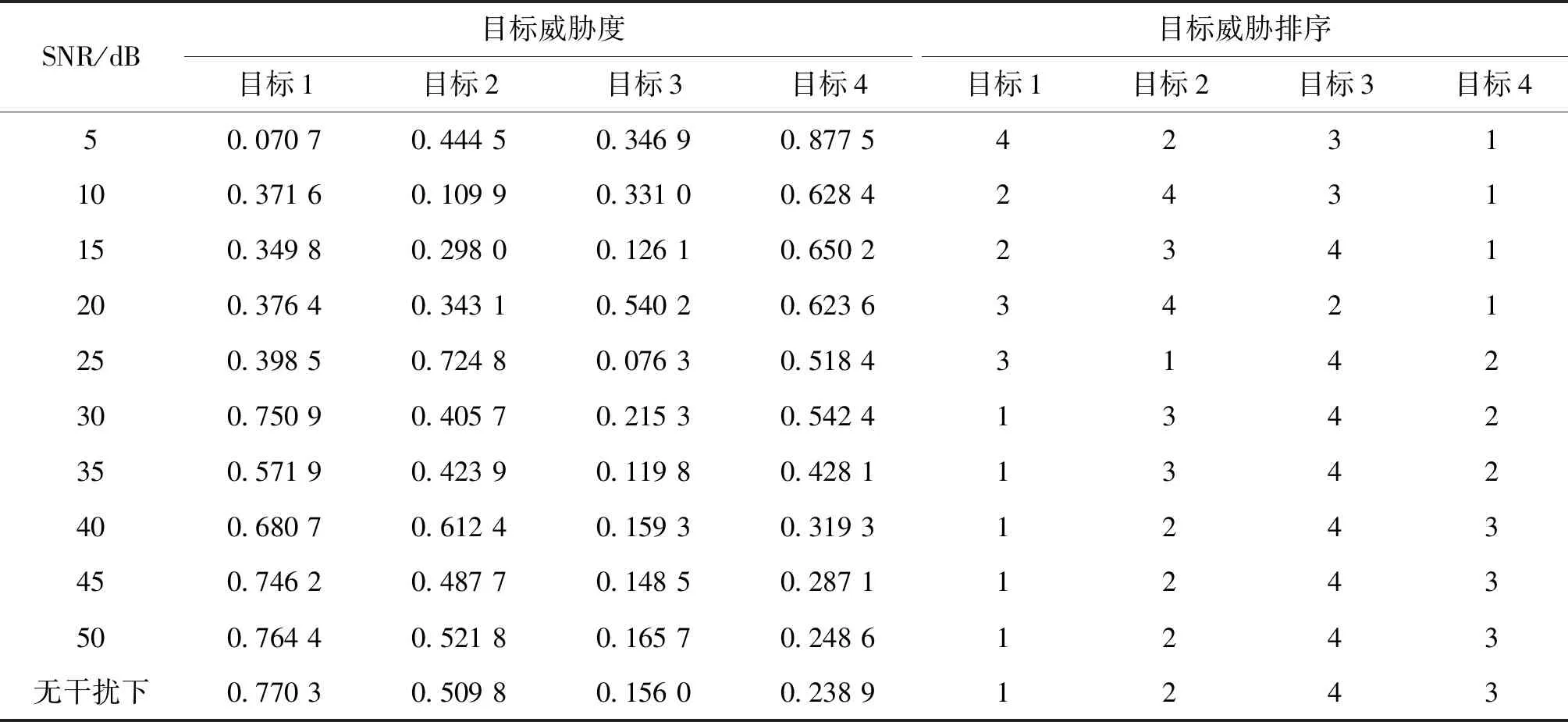
表4 某一时刻在部分干扰等级下，目标的威胁度及排序Tab.4 Threat degree and ranking of targets at certain time under partial interference levels

在干扰情况下，由于获取目标的信息含有干扰造成威胁因子的偏差，最终导致威胁度偏差。其中，在干扰等级较强的情况下，目标的威胁度与真实的目标威胁度差距较大；在低干扰情况下，目标威胁度与真实的威胁度接近，所得的目标威胁排序也保持一致。由此说明在干扰的情况下，若对信息不加以处理，则影响空战威胁评估结果。

对于多属性决策的评价，本文采用评价指标——Kendall[23]和Spearman[24]等级相关系数。两个指标主要用以统计测量两个随机变量相关性的统计值。当输入为两个排列时，反映两个排列的相似程度，其具体计算公式分别为：

(9)

(10)

式(9)、式(10)中，τ、ρ∈[-1,1]，NC为两个排序中排名相同的数量，ND为两个排序中排名不同的数量，M为目标总数，di为两个排序的等级差。当τ=1时，说明两个目标的威胁度排序是一致的；当τ=-1时，说明两个排序是不一致的；当τ=0时，说明两个目标威胁度之间相互独立。Spearman系数类似，ρ值越接近1，两个排序则越接近。

对4个目标的25组不同时刻数据仿真，最终得到4个目标在TOPSIS、TOPSIS-M、ICA-TOPSIS算法下不同信噪比下的目标威胁度排序，并均与独立无干扰指标下的TOPSIS威胁排序进行Kendall一致性和Spearman相关性系数对比分析，如图5和图6所示。在不同的干扰环境下，与真实理想的目标威胁排序结果进行一致性和相关性分析，可以得到在中低干扰的环境中(SNR>16 dB)，基于ICA-TOPSIS的目标威胁排序结果相比其他算法与真实理想的排序结果明显保持较优的一致性和相关性，即其结果更靠近理想的结果。而在强干扰的情况中(SNR<16 dB)，其目标威胁排序的结果一致性略低于其他算法。这是由于在空战环境中，低幅度目标状态信号受到目标的强干扰下，不同信号的混合由于强噪声的影响，无法通过数据的统计特性估计其源成分，但其结果与TOPSIS、TOPSIS-M算法的差距并不大。

图5 四种算法在不同噪声等级干扰下的威胁排序一致性比较Fig.5 Comparison of targets ranking consistency of four algorithms under different SNR

同时，基于ICA分离的仿真结果表明：基于ICA-TOPSIS-M的排序结果与ICA-TOPSIS的排序结果基本吻合(如图6所示的两个算法的Spearman相关性系数曲线基本重合)。这说明仅经过ICA的分离，就能获取接近不相关指标信息。为此，仿真中还通过ICA-TOPSIS与ICA-TOPSIS-M、TOPSIS的威胁评估结果的相关性检验，进一步验证了ICA算法在威胁评估中能对目标进行更加精准地威胁分析。如图7所示，ICA-TOPSIS与ICA-TOPSIS-M的相关性基本保持接近于1，而与未经过ICA分离，即输入为耦合指标的TOPSIS算法则保持较低的相关性，由此说明，ICA有较优的解耦能力。

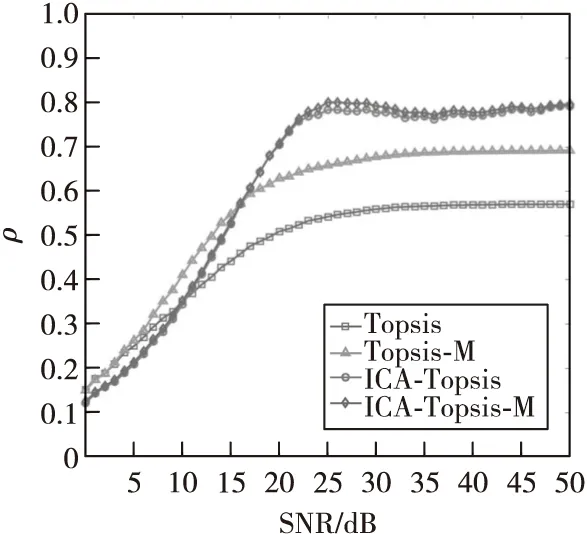
图6 四种算法在不同噪声等级干扰下的威胁排序相关性比较Fig.6 Comparison of targets ranking correlation of four algorithms under different SNR

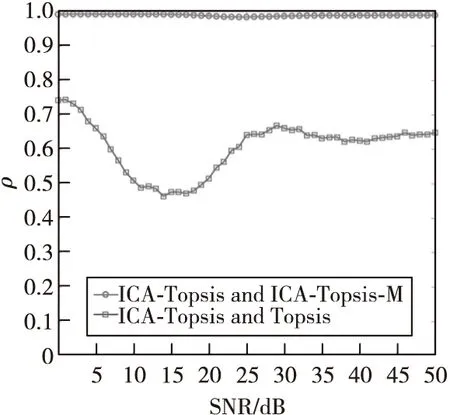
图7 ICA-TOPSIS结果的相关性检验Fig.7 Correlation test of ICA-TOPSIS results

5 结论

本文提出基于ICA-TOPSIS的空战威胁评估方法。该方法通过ICA方法进行空战干扰环境下耦合状态解耦，得到源目标独立状态的估计，用以解决传统的多属性决策算法在耦合空战状态下存在的理想解偏移而导致的威胁偏差问题。仿真实验结果表明：

1) 在传统的TOPSIS基础上，引入ICA算法进行耦合性指标的独立性估计，所得到威胁度排序与理想威胁排序有较优的一致性，较好地解决了传统算法的理想解偏移问题；

2) 本文采用FastICA算法进行独立评估指标的估计，能够快速地实现独立状态估计，同时所得到的目标威胁度排序与经过TOPSIS-M去指标相关性的威胁度排序保持高相关性，进一步验证了ICA的独立估计能力；

3) 针对不同干扰程度下的空战环境仿真，ICA-TOPSIS法相对传统的评估方法，在中低干扰环境下能保持较优的表现；在强干扰下能与传统算法保持相当的表现，进一步验证了ICA方法在空战环境下的适用性。