利用信号长驻留的隐身目标探测性能提升方法
万鹏飞,李伟龙
(空军工程大学防空反导学院,陕西 西安 710051)
0 引言
针对隐身目标的探测,现阶段取得了部分成果,例如针对目标隐身机理提出的采用发射低频信号雷达[1-3]、双多基地雷达[4-6]等反隐身技术,可以在一定程度上解决隐身目标的探测问题。但雷达采用低频信号存在探测精度差、数据率低、可靠性差的问题;双多基地雷达技术和作战使用复杂,空间探测效率低。截至目前,尚没有一项技术能够有效解决隐身目标的探测问题。
隐身目标的探测需要从多个技术方面进行针对性的优化,包括时域、频域、空域、能量域。其中传统的能量对抗,是反隐身技术研究的一个重要方向。实际情况中,目标往往是处于不同的运动状态,其相对雷达视线的姿态角时刻都在变化,导致雷达接收到的回波信号发生起伏,而隐身目标的这种起伏更为严重。为了解决雷达在对隐身目标进行探测时回波信号起伏较大的问题,从能量对抗的角度提出了利用信号长驻留的隐身目标探测性能提升方法。
1 信号长驻留
1.1 长驻留信号的概念
信号长驻留主要包括跟踪雷达的驻留时间和驻留探测。
1) 驻留探测:所谓驻留探测,主要针对相控阵跟踪雷达而言,是指天线处于不扫描状态,维持波束指向不变,对目标进行连续探测。
2) 驻留时间:在雷达进行驻留探测过程中,信号的发射总时间称为驻留时间。
常规雷达信号的驻留时间由所要求的目标探测距离范围决定,假设要求雷达探测的最大距离为Rmax,则常规雷达信号的驻留时间T通常在2Rmax/c~4Rmax/c范围内。
而长驻留信号要求驻留时间T≫2Rmax/c,通常取T≥10×2Rmax/c,即通过增长驻留时间提高雷达发射信号能量,从而增大雷达的探测距离范围,使雷达能够探测到更远更小的目标。
1.2 驻留时间与雷达作用距离的关系
雷达对目标的探测性能从根本上来说取决于接收信号的信噪比。而目标的RCS变化是影响接收信号信噪比的重要因素,决定了雷达能在多大距离上发现目标。
由式(1)所示雷达方程可得,雷达作用距离的大小取决于雷达发射机、接收系统、天线等分机参数,同时又和目标的性质及环境因素有关。
(1)
式(1)中,Pt为雷达发射功率,G为雷达天线的增益,λ为发射信号波长,σ为目标散射的雷达截面积,Simin为最小可检测信号功率。
从雷达方程可以看出,雷达作用距离与发射功率和雷达目标截面积成正比,与最小可检测信号功率成反比。而Simin又可表示为:
(2)
式(2)中,k为玻尔兹曼常数,T0=290 K,Bn为通带带宽,Fn为接收机的噪声系数。
现代雷达多采用复杂的信号波形,波形所包含的信号能量往往是接收信号可检测性的一个更合适的度量。例如,匹配滤波器输出端的最大信噪功率比等于Er/N0,其中Er为接收信号的能量,N0为接收机均匀噪声谱的功率谱密度,在这里以接收信号能量Er来表示信号噪声功率比值。从一个简单的矩形脉冲波形来看,若其宽度为τ、信号功率为S,则接收信号能量Er=Sτ;噪声功率N和噪声功率谱密度N0之间的关系为N=N0Bn,其中Bn为接收机噪声带宽,采用简单脉冲信号时,可认为Bn=1/τ。这样可得到用能量表示的雷达方程:
(3)
式(3)中,CB为带宽校正因子,它表示接收机带宽失配时所带来的信噪比损失,通常CB≥1,匹配时CB=1。L表示雷达各部分损耗引入的损失系数。
由式(3)可以看出在其他参数不变的情况下,提高雷达的辐射能量能够有效提高雷达的作用距离。
2 信号长驻留对隐身目标探测性能的提升方法
分析信号常驻留对隐身目标的探测性能,首先需要对隐身目标的RCS特性进行仿真建模,然后研究信号长驻留对隐身目标起伏特性的探测性能。
2.1 隐身目标特性
1)隐身目标RCS起伏特性
目标的起伏特性[7]是雷达系统探测、跟踪、识别目标必须考虑的因素。回波的起伏[8-9]总是与目标的雷达散射截面积(RCS)相联系,而RCS是雷达测量中的重要参量之一,隐身目标通过控制和降低自身雷达特征,减小雷达散射截面积的方法来降低探测雷达的作用距离,从而达到有效提高突防能力和生存概率的目的。图1为探测雷达俯仰角保持不变,方位角从0°~360°扫描,得到的对非隐身目标和隐身目标的RCS仿真曲线。
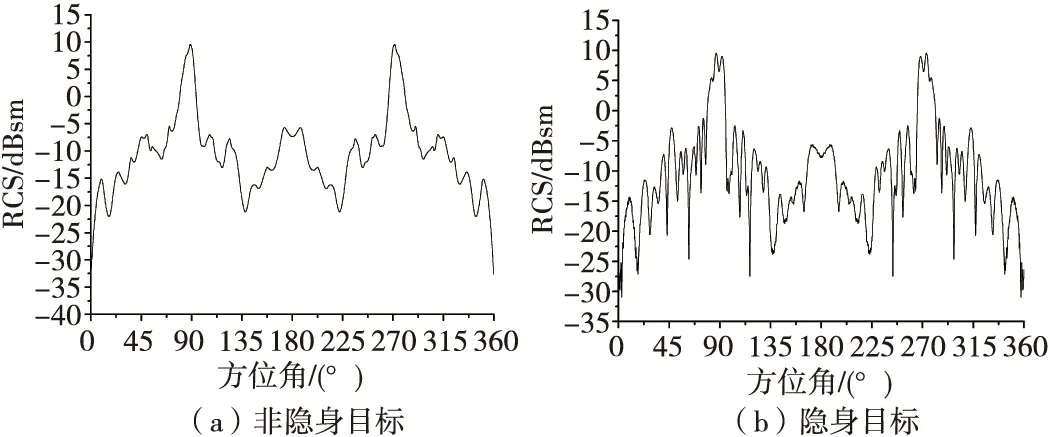
图1 全方位RCS变化情况Fig.1 The whole airspace RCS variation
从图1可知,随着雷达方位角的变化,目标RCS出现较大起伏,在目标正前方(方位角为0°)和正后方(方位角为180°)±30°范围内RCS较小,两翼(方位角为90°和270°)±10°范围内RCS较大。比较图1(a)和图1(b)可以发现,全方位上隐身目标相对非隐身目标RCS起伏剧烈,具有快起伏特点,这对雷达目标探测非常不利,极易造成跟踪目标丢失。
2) 常用RCS起伏模型
为了准确地描述目标雷达截面积的起伏特性,需要知道RCS的概率密度函数和相关函数,然后建立相应的起伏统计模型[10]。W.Weinstock等人提出一种通用性较强,符合实际目标测量数据的起伏模型——χ2统计模型,此模型下雷达截面积服从χ2分布的概率密度函数为[11]:
(4)

施威林目标起伏模型是χ2分布统计模型的特例,当m=1时,相当于施威林Ⅰ、Ⅱ类目标分布,其概率密度函数为:
(5)
式(5)的模型适用于复杂目标是由大量近似相等单元散射体组成的情况。Ⅰ类为快起伏,Ⅱ类为慢起伏。
当m=2时,相当于施威林Ⅲ、Ⅳ类目标分布,其概率密度函数为:
(6)
式(6)适用于目标是由一个较大反射体和许多小反射体合成,或者一个大的反射体在方位上有小变化的情况。Ⅲ类为快起伏,Ⅳ类为慢起伏。
m趋于无穷大时,相当于不起伏目标。
3) 隐身目标RCS起伏模型
大多数运动目标的RCS起伏统计特性都近似满足式(5)表示的概率密度函数,即服从指数分布,例如常规飞机等非隐身目标;还有的目标比较接近于对数正态分布,例如船舶等。
对于隐身目标,在信号的驻留时间内RCS起伏通常并不是单一服从某个指数分布,而是多个服从相同分布RCS的叠加,因此,用多个相互独立同分布叠加后的概率密度函数能更好表现隐身目标RCS的起伏情况。
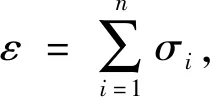
(7)
式(7)即为多个服从同分布RCS叠加后的概率密度函数,它能更好地表示隐身目标RCS的起伏情况。接下来基于式(7)的模型分析长驻留信号对快起伏目标的探测性能影响。
2.2 探测性能提升方法
隐身目标由于其RCS极小并且具有强起伏特性,导致雷达不容易检测出目标,上文已经对信号长驻留与雷达作用距离的关系进行了分析,本节提出信号长驻留信号提高雷达隐身目标探测性能的方法。
1)提升雷达作用距离
雷达使用各种复杂脉压信号的情况,只要知道脉冲功率及发射脉宽就可以用来估算作用距离而不必考虑具体的参数。由于脉冲功率一般受到发射机的限制,不能过大,所以考虑增加发射信号的脉宽来提高雷达的检测性能。
雷达发射长驻留信号相当于增加发射信号的等效脉宽,从而通过提高信号能量使雷达的探测距离增大。图2给出了常规雷达最大可探测距离与发射信号驻留时间的关系曲线。从图中可以看出,随着驻留时间的增长雷达最大可探测距离逐渐增大。
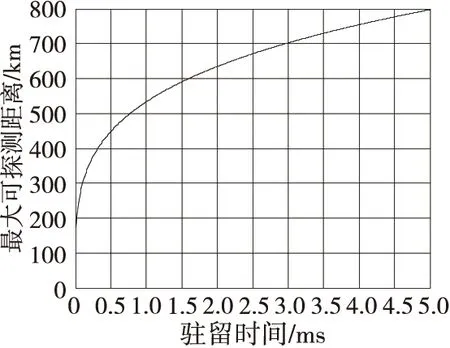
图2 最大可探测距离与驻留时间关系曲线Fig.2 The relationship curve between maximum detectable range and dwell time
2)提升雷达探测概率
雷达信号的接收和处理过程一直受噪声影响,而噪声是一种随机过程,所以噪声中的信号检测也是一种随机事件。对于雷达信号来讲,当没有目标时,接收机输出噪声一般情况下服从均值为零,方差为μ的正态分布;当有目标信号存在时,接收机输出目标加噪声信号,其均值大于零,仍服从正态分布。对于窄带噪声信号,其包络幅度服从瑞利分布。
匹配滤波器的输出具有平方律特性,信号包络的幅度服从指数分布:
无目标:
(8)
有目标:
(9)
设U0为门限判决电平,可得:
虚警概率:
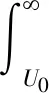
(10)
检测概率:
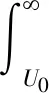
(11)
假设在虚警概率Pf=10-6,目标RCS=0.02 m2,图3给出了驻留4 ms和40 ms条件下雷达作用距离与接收机输出最小可检测信噪比的关系曲线;图4给出了驻留4 ms和40 ms条件下雷达作用距离与探测概率的关系曲线。
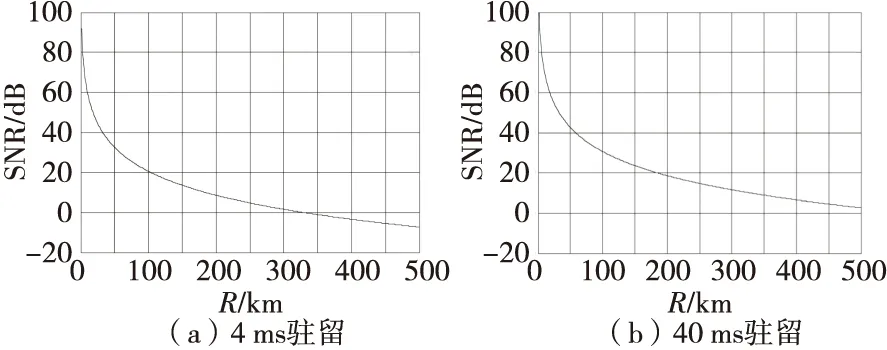
图3 作用距离与输出最小可检测信噪比关系Fig.3 The relationship between the detection distance and minimum detectable SNR
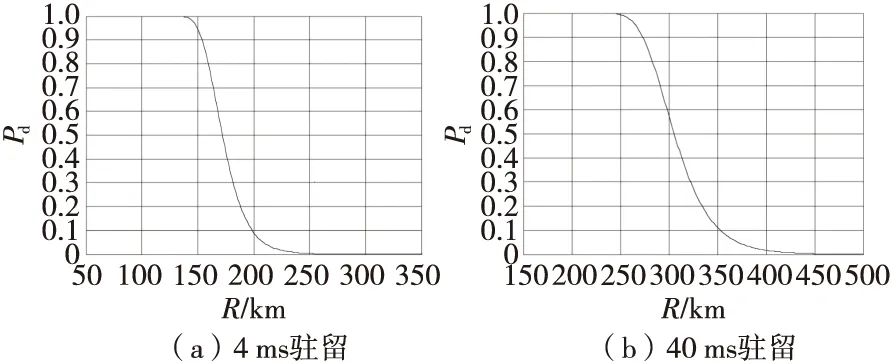
图4 作用距离与探测概率的关系Fig.4 The relationship between the detection distance and detection probability
图3反映了同一信噪比条件下,驻留40 ms的信号比驻留4 ms的信号具有更大的雷达作用距离;图4反映了对同一距离上的目标进行探测时,驻留40 ms的信号比驻留4 ms的信号探测到目标的概率更大。因此,长驻留信号比常规雷达信号具有更好的探测性能。
3 仿真分析
雷达发射长驻留信号对目标进行探测时,接收机将经目标RCS调制的长驻留回波信号作为一个整体进行匹配滤波处理,因此具有抗目标快起伏的潜力。图5给出了雷达从发射长驻留信号到接收处理的示意图。
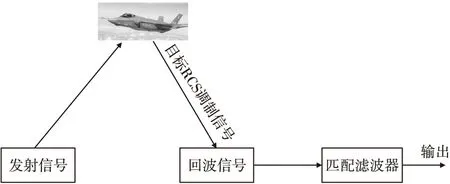
图5 雷达信号发射到接收处理示意图Fig.5 Diagram of the radar signal emission to the receiving processing
仿真中假设匹配接收机理想匹配,即忽略目标运动带来的影响。通过设置不同的RCS起伏频率来控制目标雷达截面积的起伏快慢,并利用式(4)产生一组RCS随机数据作为回波信号包络,然后进行匹配处理输出信号。假定目标起伏频率100 Hz,分别用4 ms和40 ms驻留信号对目标进行探测,图6给出了4 000 ms内不同时长驻留回波输出信号的起伏情况。
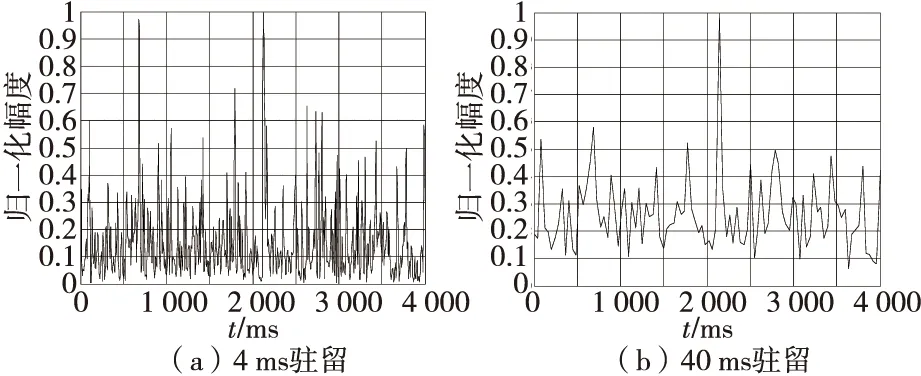
图6 不同时长驻留回波输出信号起伏情况Fig.6 The fluctuation of different dwell time echo output signal
从图6中可以看出,4 ms驻留时输出信号起伏很大,而40 ms驻留时输出信号起伏明显减小,并且平均输出归一化幅度增大,在保证相同探测概率的条件下相当于增大了目标探测距离。因此,当目标RCS起伏频率为100 Hz时,40 ms驻留相对4 ms驻留不仅能够有效抑制目标回波起伏,而且增大了雷达的作用距离。
下面通过设置不同的起伏频率,进一步分析长驻留信号抗目标起伏特性,图7给出了目标RCS起伏频率分别为100、50、25、10 Hz时,4 ms驻留(左图)和40 ms驻留(右图)回波输出信号归一化幅度的变化情况。
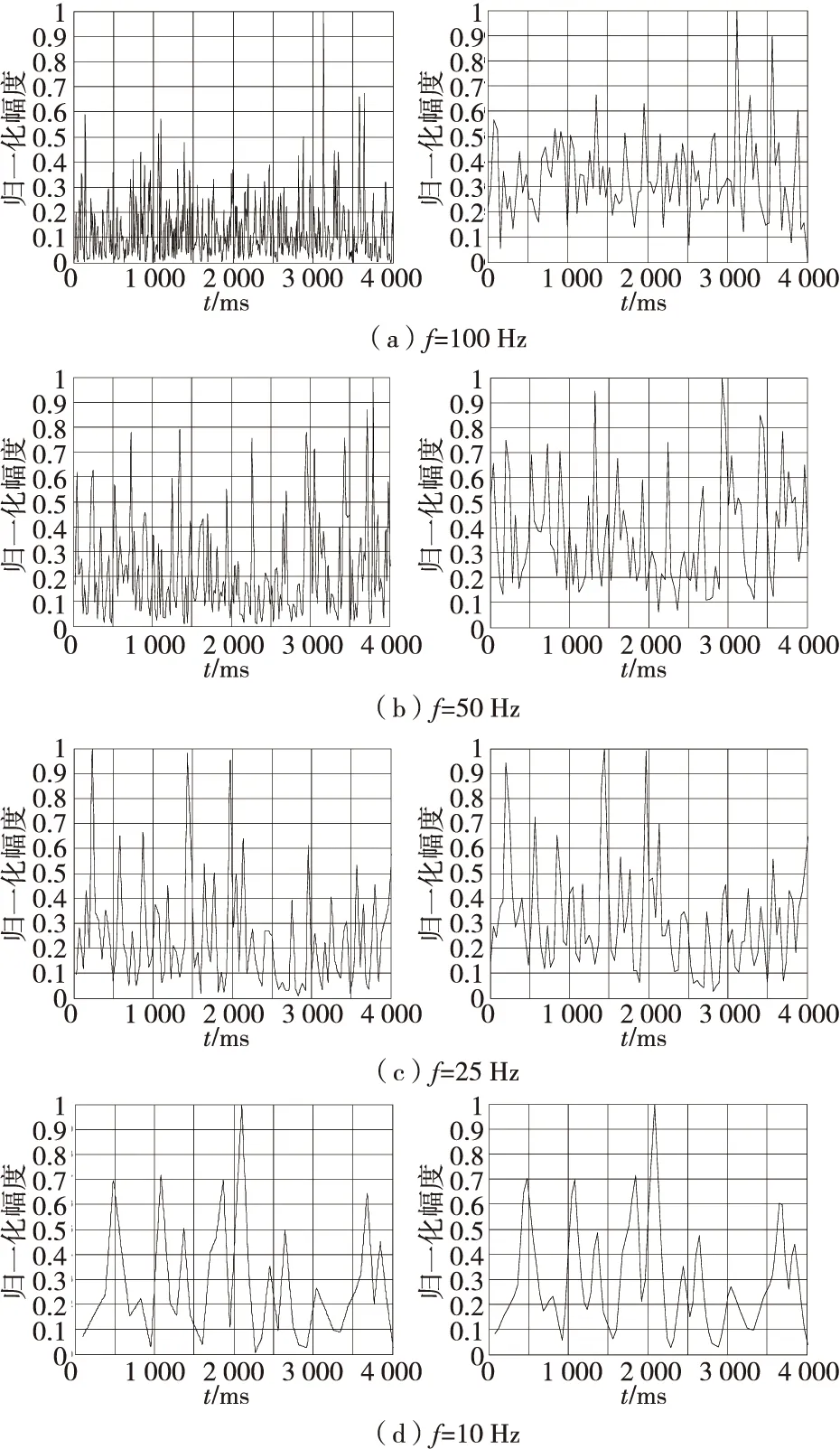
图7 4 ms驻留和40 ms驻留回波输出信号Fig.7 The 4 ms dwell and the 40 ms dwell signal echo output signal
从图7可以看出,当目标RCS起伏频率较高时,输出信号幅度起伏较大,随着起伏频率的降低,输出信号幅度起伏逐渐减小。通过对比4 ms驻留和40 ms驻留回波输出信号归一化幅度前后变化情况可以发现,在目标RCS起伏频率较大时,40 ms驻留相对4 ms驻留回波输出信号起伏明显降低,并且平均输出归一化幅度增大,能够有效减小目标RCS起伏带来的影响,随着起伏频率的降低,长驻留信号抗起伏效果逐渐减弱。通过多次设置不同的起伏频率仿真长驻留信号抗起伏特性效果得到:当起伏频率降到10 Hz以下时,40 ms驻留信号与4 ms信号匹配输出几乎一样,事实上,此时目标RCS起伏已经很小,在信号驻留时间内RCS起伏对输出信号的影响非常小,没有必要采用长驻留信号进行探测。
为了更加直观地反映长驻留信号抗目标起伏特性,从雷达作用距离改善程度的角度考虑,从图7可以看出,40 ms驻留时回波输出信号平均归一化幅度增大,在保证相同探测概率的条件下,相当于增大了雷达作用距离。为了体现这种变化,这里定义一个距离改善因子参量δ,表示长驻留和常规驻留两种状态下雷达作用距离之比。以4 ms驻留时雷达作用距离作为基准,表1给出了不同驻留时间和不同目标RCS起伏频率下距离改善因子的大小。
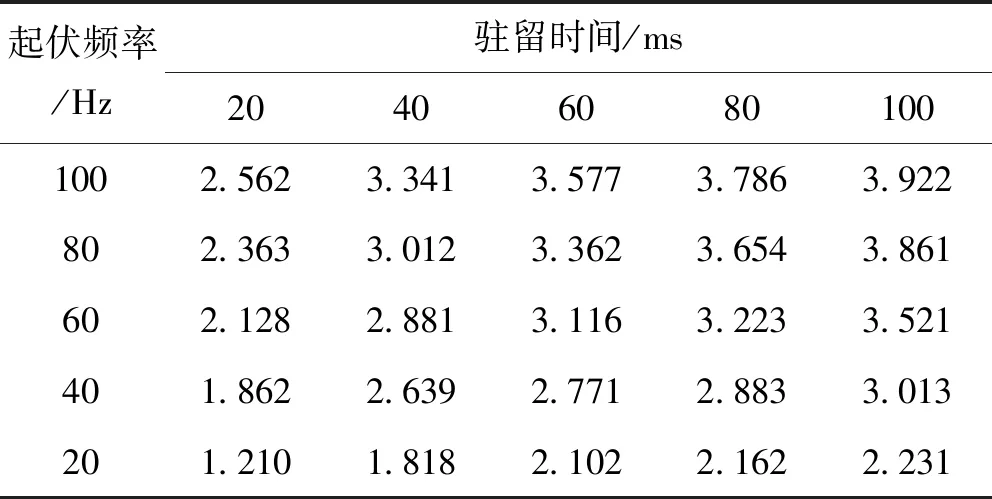
表1 不同驻留时间和起伏频率下距离改善因子Tab.1 The distance improvement factorof under different dwell time and RCS fluctuating frequency
从表1中可以看出,距离改善因子随着驻留时间的增大而增大,并且随着目标RCS起伏频率的减小也呈下降趋势。结果表明,同一目标相同RCS起伏频率下,信号驻留时间越长,目标作用距离越远,抗目标起伏效果越明显,并且对RCS起伏频率大的目标,改善程度更好。因此,长驻留信号能够有效对抗隐身目标快起伏特性。
4 结论
本文通过分析隐身目标起伏特性建立了隐身目标起伏模型,提出利用信号长驻留提升对隐身目标探测性能的新方法。该方法通过提高信号的驻留时间从而提升雷达作用距离和探测概率。仿真结果表明,信号长驻留相对常规雷达信号能够在有效抑制隐身目标回波信号起伏的同时,显著提高雷达的探测性能。下一步将针对雷达辐射的不同波形在长驻留下的信号处理方法进行研究。

