五阶IIR低通数字滤波器的性能*

周 旋，邬云文

(1.吉首大学信息科学与工程学院，湖南 吉首 416000；2.湖南省普通高校近地空间电磁环境监测与建模重点实验室，湖南 长沙 410114；3.吉首大学物理与机电工程学院，湖南 吉首 416000)

数字滤波器因具有高精度、高可靠性、复用等优势，被应用于手机通信、传感器网络通信、自动控制、医疗、军事、发电供电等诸多领域[1-2].如适用于集群系统的以氧化镁为衬底的集群超导滤波器和以铝酸镧为衬底的滤波器，它们都具插入损耗低、带边陡度高、带外抑制好等优势，对所需信号有更高的选择性，能减少来自相邻信道信号的干扰，特别是高温超导滤波器，还有降低系统噪声系数及提高检测微弱信号的能力[3].又如运用Verilog HDL语言、基于FPGA设计的3 级 CIC 滤波器，与传统结构的 3 级 CIC滤波器相比，它的硬件资源节省可达 35.48%，且每个寄存器的位宽可变[4].再如具有宽阻带特性的四陷波超宽带滤波器[5-7]和应用于电动滑台位置实时补偿的卡尔曼滤波器[8-9].这些滤波器在各行各业中均发挥了不可忽视的作用，其特性是值得研究的，但学者的研究多集中在滤波器的通带特性，而对于过渡带和阻带特性的分析尚有欠缺.因此，笔者拟以五阶IIR数字低通滤波器为例，结合时域特性、频响特性和Z域特性等，重点分析该滤波器过渡带和阻带的特性，以期充实数字滤波器过渡带和阻带特性研究的相关理论.

1 理论分析

(1)

其中T为周期.由(1)式推导出s域与Z域的映射关系为s=σ+jΩ，z=rejω，这里Ω为s域角频率，于是

对于s平面虚轴，有σ=0，s=jΩ，r=1，于是

(2)

其中ω为z平面角频率，Ω为s平面角频率.在求解模拟滤波器的指标时，利用(2)式进行预畸变处理.根椐巴特沃斯经典滤波器转换设计数字滤波器的方法，幅频特性定义为

(3)

阻带最小衰减As和通带最大衰减Rp分别为

(4)

(5)

由(3)～(5)式及巴特沃斯滤波器特性经典理论，可得

(6)

(7)

由(6)，(7)式，可得滤波器阶数N与通带最大衰减Rp、阻带最小衰减As、通带边界角频率Ωp和阻带边界角频率Ωs的关系式：

(8)

双线性变换法要求将s域Ωs，Ωp值从0到±SymboleB@的分布压缩至0到±π之间，s和z的对应转换关系式为

(9)

2 实验设计

本研究所讨论的五阶IIR数字低通滤波器，其通带边界频率ωp=0.25π rad/s，通带最大衰减Rp=1 dB，阻带最小衰减As=15 dB，阻带边界频率ωs=0.4π rad/s，滤波器采样频率fs=100 Hz.

因为数字滤波器的传输函数只与频域的相对值有关，所以先利用(2)式对滤波器设计指标进行预畸变处理，将数字指标转换为中间模拟滤波器指标.为了方便分析，先求解五阶低通巴特沃斯滤波器的归一化频率，求解公式为

(10)

图1 五阶IIR数字低通滤波器设计流程Fig. 1 Design Process of Fifth Order IIR Digital Low-Pass Filter

根据(8)～(10)式求出阶数N，同时得到模拟滤波器系统函数

运用双线性变换法将五阶模拟滤波器系统函数转换为数字滤波器系统函数，即将五阶低通巴特沃斯滤波器系统函数H(s)转换为数字滤波器系统传输函数H(z)，得到

五阶IIR数字低通滤波器设计流程如图1所示.

3 仿真结果与讨论

为了研究五阶IIR数字低通滤波器的性能，采用Matlab软件对其在理想环境下的特性进行仿真，仿真结果如图2所示.

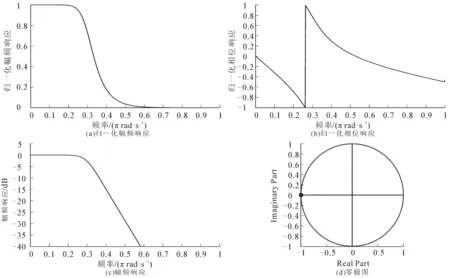
图2 五阶IIR数字低通滤波器特性Fig. 2 Characteristics of Fifth Order IIR Digital Low-Pass Filter

由设计方案可知，通带边界频率ωp为0.25π rad/s，阻带边界频率ωs为0.4π rad/s，通带为0～0.25π rad/s，阻带为0.4π～π rad/s，过渡带为0.25π～0.4π rad/s.由图2(a)可见，最大通带幅度偏离即通带幅度的最小值为0.891 3，最大阻带幅度为0.177 8.

令该滤波器通带最大衰减

(11)

其中ε为波纹参数，δp为通带误差容限(通带波纹峰值).由(11)式可得

(12)

(13)

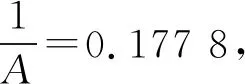
由图2(b)可见：当频率为0～<0.25π rad/s时，归一化相位值为负数，而该滤波器的通带为0～<0.25π rad/s，说明滤波器在通带范围内出现相位延迟，且随着频率的增加延迟越来越大；当频率为0.25π rad/s时，相位翻转180°，由延迟最大值变为超前最大值；之后频率再增加，滤波器将通过过渡带进入阻带区间，相位超前量逐渐减小；当频率在0.5π rad/s附近时，传输信号相位差回到0，此时所有信号同步但不在滤波器传输范围.综合图2(b)和(c)可见：当进入阻带即该数字滤波器的幅度衰减至15 dB时再次变为相位滞后，且滞后量逐渐增加.

由图2(c)可见：当频率为0～<0.25π rad/s时，幅度无衰减；当频率为0.25π～<0.4π rad/s时，幅度响应呈非线性衰减，该区域为过渡带；当频率为0.4π～π rad/s时，幅度响应呈线性衰减，该区域为截止带.

由图2(d)可见：零点处于单位圆上但与极点距离较远，故该滤波器通带较窄；频率响应峰值为0；极点关于坐标轴的横轴呈对称分布.

综上分析，由图2可知：

(1)在通带和阻带截止频率处的参数为Rp≤1 dB，As≥15 dB，系统的极点都在单位圆内，是一个稳定的系统.

(2)当频率为0.25π rad/s时出现相位反转，进入过渡区，信号幅度陡降，相位由滞后突变为超前，传输的信号包络坍塌崩溃，此时系统不稳定；当频率不小于0.4π rad/s时进入截止区，相位由超前逐渐变为延迟，且当频率在0.5π rad/s附近时，传输信号相位差回到0，此时所有信号同步但不在滤波器传输范围.

(3)当幅度响应衰减为0后，系统信号传输仍存在相位变化，即中高频段仍有微量信号通过，此现象属于数字滤波器的正常误差，不影响该数字滤波器的正常滤波功能.

4 结论

在现有滤波器经典理论基础上，以五阶IIR数字滤波器为例，重点分析了其过渡带和阻带特性.分析结果如下：

(1)利用信号与系统经典理论，推导出滤波器阶数N与通带最大衰减Rp、阻带最小衰减As、通带边界角频率Ωp、阻带边界角频率Ωs的关系式.

(2)该滤波器的相位特性为在通带内延迟随着频率的增加而增加.当频率为0.25π rad/s时出现相位反转突变，传输的信号包络坍塌崩溃，当频率在0.5π rad/s附近时，传输信号相位差回到0，此时所有信号同步但不再传输.幅度响应衰减为0时，系统中仍有微量的中高频信号通过，这属于正常误差范围.