非等纹响应低通滤波器研究
高山山,徐嘉莉
(成都大学 电子信息工程学院,四川 成都 610106)
0 引 言
随着无线通信系统的快速发展,对低通滤波器提出了更高的要求.过去的研究中,研究者们主要集中于研究通带内具有等纹响应的低通滤波器.然而,由于加工误差等因素的影响,滤波器在通带内的插入损耗会增大,该现象在通带到阻带的过渡带附近尤为严重.近年来,一些研究者开始用不同的方法在带通滤波器上实现非等纹响应,如链状函数滤波器[1-4]、圆顶信封函数滤波器[5]、短路支节带通滤波器[6]、平行耦合线带通滤波器[7].在此基础上,本研究设计了一种非等纹响应的低通滤波器,相比于传统的等纹响应低通滤波器,该滤波器具有更加优良的性能.
1 传统切比雪夫低通滤波器
切比雪夫响应在通带内表现为等纹特性,在阻带内呈最大平坦特性.对于一个n 阶切比雪夫响应的低通滤波器而言,它的插入损耗可表示为[8],
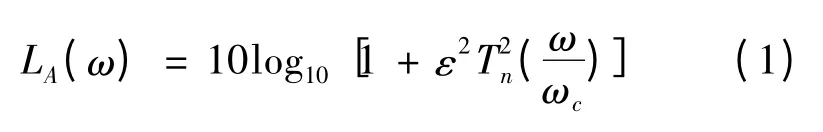
其中,

Tn(x)为n 阶的第一类切比雪夫函数多项式.
一个7 阶的切比雪夫函数多项式为,
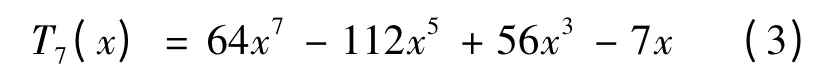
若设置该7 阶切比雪夫函数低通滤波器通带内的反射波瓣值为-10 dB,可得到该滤波器的响应曲线如图1 所示.
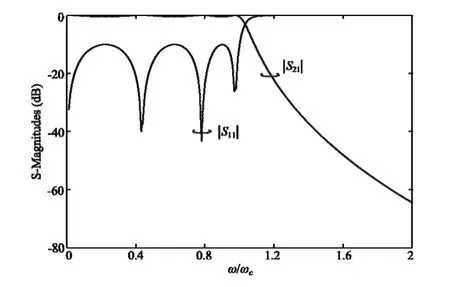
图1 传统切比雪夫响应曲线
由图1 可知,该滤波器在通带内具有等纹的特性,通带内3 个反射波瓣值均在-10 dB.
2 非等纹响应低通滤波器
本研究基于非等纹响应带通滤波器的综合设计方法,设计出了一种7 阶非等纹响应的低通滤波器,其插入损耗可以表示为,
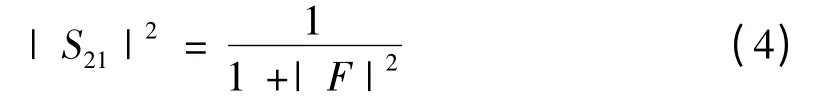
其回波损耗可表示为,
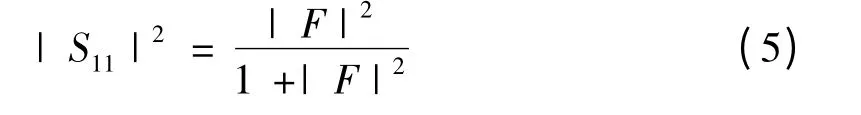
其中,F 为特征函数多项式.
对于传统切比雪夫响应低通滤波器而言,通带内具有等纹的特性.而对于非等纹响应的低通滤波器,通过调节特征函数多项式的系数,可以改变通带内反射波瓣的值,将通带内的反射波瓣设置为不全部相等,即实现非等纹响应低通滤波器的特性.本研究以7 阶低通滤波器为研究实例.从图1 可以看出,该切比雪夫响应低通滤波器在通带内具有3 个反射波瓣,设第1 个反射波瓣的值为RL1,第2 个反射波瓣的值为RL2,第3 个反射波瓣的值为RL3.对于切比雪夫响应低通滤波器而言,通带内3 个反射波瓣值全部相等,即RL1= RL2= RL3.对于非等纹响应低通滤波器,通带内的反射波瓣值不再全部相等,即RL1≠RL2≠RL3,此时,可得特征函数F 的表达式为,
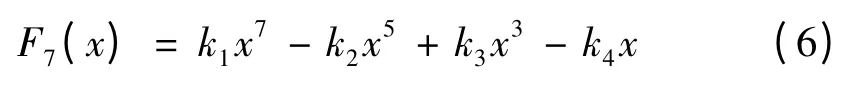
通过调节特征函数F 的系数,可将低通滤波器通带内的反射波瓣设置在指定值.本设计中,设定通带内反射波瓣值分别为,RL1=-10 dB、RL2=-15 dB、RL3=-20 dB,可建立7 个满足边界条件的方程为,

其中,F1、F2、F3分别对应于反射波瓣值等于RL1、RL2、RL3时F 函数的值.通过求解式(7)~(13)的非线性方程组,可以求得系数k1、k2、k3、k4的值.通过综合得到该滤波器的特征函数多项式为,
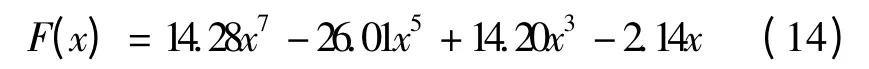
该滤波器的响应曲线如图2 所示.采用相同的综合设计方法,可以综合得到RL1=- 15 dB、RL2=-20 dB、RL3=-25 dB 时的特征函数多项式为,
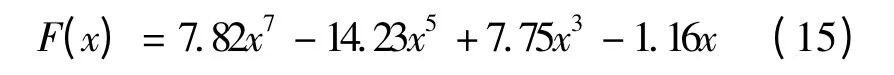
此时,滤波器的响应曲线如图3 所示.
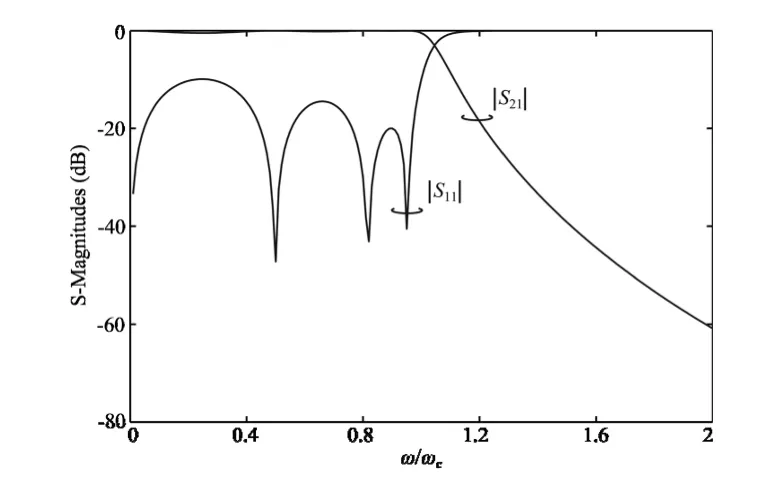
图2 非等纹响应曲线
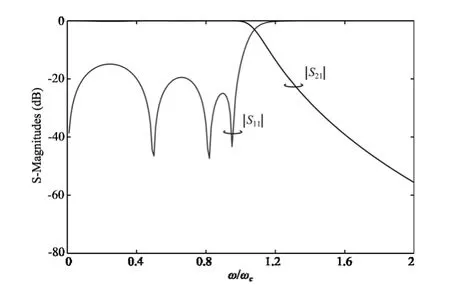
图3 非等纹响应曲线
从图2、图3 都可以看出,该滤波器的响应特性曲线在通带内具有非等纹的特性,通过调节特征函数多项式的系数,可以控制通带内反射波瓣的值.同时,在靠近通带边沿部分反射波瓣值较低,这样可以很好地解决滤波器在实际加工过程中由于加工误差带来的通带内插入损耗增加的问题.
3 结 论
本研究设计了一种非等纹响应的低通滤波器.通过调节特征函数的系数,可实现低通滤波器在通带内的非等纹特性.与传统的切比雪夫函数滤波器相比,该滤波器具有更加优良的性能.
[1]Guglielmi M,Connor G.Chained function filters[J].IEEE Microw Guided Wave Lett,1997,7(12):390-392.
[2]Chrisostomidis C E,Guglielmi M,Young P,et al.Application of chained functions to low-cost microwave bandpass filters using standard PCB etching techniques[C]//Proceedings of 30th European Microwave Conference.Paris,France:EUMA,2000:40-43.
[3]Chrisostomidis C E,Lucyszyn S.On the theory of chainedfunction filters[J].IEEE Trans Microw Theory Tech,2005,53(10):3142-3151.
[4]Chrisostomidis C E,Lucyszyn S.Seed function combination selection for chained function filters[J].IET Microw Ant Prop,2010,4(6):799-807.
[5]Jayyousi A B,Lancaster M J,Huang F.Filtering functions with reduced fabrication sensitivity[J].IEEE Microw Wir Comp Lett,2005,15(5):360-362.
[6]Sun S,Gao S S.Design and implementation of ultra-wideband bandpass filter with non-equiripple responses[C]//IEEE MTT-S Int Microwave Symp.Seattle,USA:IEEE Press,2013.
[7]Gao S S,Sun S.Synthesis of wideband parallel-coupled line bandpass filters with non-equiripple responses[J].IEEE Microw Wir Comp Lett,2014,24(9):587-589.
[8]Zhu L,Sun S,Li R.Microwave bandpass filters for wideband communications[M].Hoboken,NJ,USA:John Wiley & Sons,2012.

