一种小线段平滑过渡轨迹控制算法的实现

林 峰，郑力新

(1.福建商业高等专科学校 信息管理工程系，福建 福州 350012;2.华侨大学 工学院，福建 泉州 362021)

0 引 言

在数控加工系统中，对于加工工件的曲面通常采用直线段进行逼近，即把待加工的图形分解成一系列的小线段后，再由数控系统中的控制器对每个小线段进行插补运算.为了保证加工精度，传统的直线插补算法在每个小线段之间进行加减速处理，使加工每条小线段时的初始速度和终止速度都为零.这种方式必然造成系统的频繁启停，使得加工效率低，且加工的质量不高.为了解决这些问题，科研人员相继开展了小线段过渡技术的研究，并取得了一定成果［1－6］.为了进一步提高小线段的加工效率，使小线段之间的过渡更为平滑，本研究提出了一种小线段平滑过渡算法，使其能够应用于一般的控制器中，从而在满足加工精度和机械特性的条件下，提高工件的整体加工效率.

1 圆弧过渡的数学模型

如图1 所示，由点Pi－1、Pi、Pi+1所构成的线段Pi－1Pi、PiPi+1分 别 为2 条 相 邻 的 小 线 段，圆 弧为在两线段之间插入的过度曲线，其中Q0、Q2分别为圆弧在线段Pi－1Pi、PiPi+1上的切点，Q1为圆弧的中点.为了分析圆弧与两线段之间的关系，如图2 所示，首先建立一个以Q0为原点、以为X 轴正向和以为Y 轴正向的坐标系.假设加工路径为Pi－1→Pi→Pi+1，Pi为线段之间的拐角点，按照这个顺序取向量为和，则将2 个向量之间的夹角作为线段之间的夹角.在这个顺序下，Q0即为过渡圆弧的接入点，而Q2即为过渡圆弧的转出点.

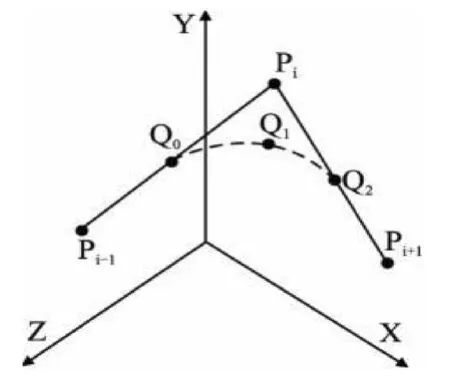
图1 圆弧过渡示意图

图2 圆弧过渡坐标系

图2 中，△Q0OQ2为等腰三角形，从而可以推出△Q0PiQ2也为等腰三角形，因此拐角点Pi到接入点Q0和转出点Q2的距离是相等的，即Pi到接入点Q0和转出点的距离称为线段Pi－1Pi和PiPi+1完成圆弧过渡所需的最小长度，这里称它为过渡距离.由于线段PiQ1垂直于圆O 上过点Q1的切线，所以线段PiQ1的长度为拐角点Pi到过渡圆弧的最短距离，称之为轮廓误差.

假定线段Pi－1Pi与PiPi+1的长度分别为Si和Si+1，且它们之间的夹角为α，过渡圆弧半径为r，圆心角为φ，拐角点Pi到圆弧的最短距离为e，以及完成圆弧过渡所需的过渡距离为l.根据几何知识，可以得到下面这组式子，

通过式(1)就可推导出相邻小线段之间的夹角α、小线段的过渡距离l、拐角点到过渡圆弧的最短距离e 以及过渡圆弧的半径r 之间的关系为，

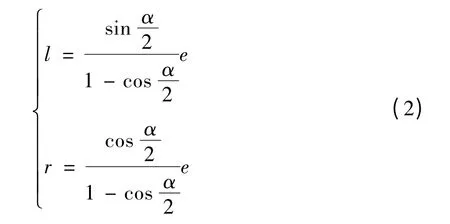
2 圆弧过渡算法

采用插入圆弧的方式来实现相邻小线段之间的平滑过渡时，实际加工路径与原始加工路径会有一定偏差.首先，需要满足的就是使加工的轮廓误差在允许范围之内，根据轮廓误差、两线段夹角和线段长度就可以确定过渡圆弧的半径以及接入点和转出点，然后通过两线段的向量关系得出过渡圆弧的旋转方向，其次，是在过渡圆弧上的进给速度需满足加工平台的机械特性，根据所允许的最大加速度即可算出最大进给速度.最后，计算出全路径上的数据并与控制器的插补指令相结合，即可实现小线段的平滑过渡.

2.1 过渡圆弧半径和接入点、转出点的确定

在两线段间插入过渡圆弧后，实际加工路径将不同于原始加工路径，因此存在着一定的轮廓误差.这个轮廓误差的最大值就是拐角点到过渡圆弧中点的距离.为了使加工精度能够满足要求，在确定过渡圆弧的半径和接入点、转出点时需考虑它的轮廓误差，因此取最大轮廓误差Em来限制过渡圆弧的参数.将Em代入式(2)中，可以得到由最大轮廓误差所限制的过渡距离lc为，

由于式(3)是建立在图2 的数学模型之上，且实际的Em取值会远远小于线段长度，因此最大轮廓误差Em限制的过渡距离lc一定小于相邻线段的长度.

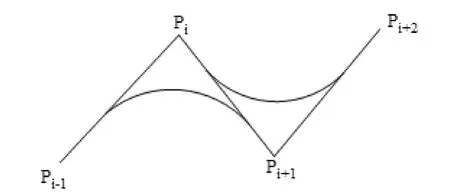
图3 线段自身长度限制示意图

如图3 所示，任意3 条连续的小线段Pi－1Pi、PiPi+1、Pi+1Pi+2构成了2 个相邻的拐角，它们之间存在公共线段PiPi+1，因而2 个拐角在公共线段PiPi+1上的过渡距离可能发生重叠的情况，即后一个过渡圆弧的接入点位置在前一个过渡圆弧转出点之前，所以过渡圆弧的半径和过渡距离不仅受到最大轮廓误差的限制，还受到小线段自身长度的限制.假设受到线段自身长度限制的过渡距离为ls，且每条小线段上的过渡距离不超过自身长度的一半，则有，

为了使如图1 所示的小线段Pi－1Pi和PiPi+1之间的过渡圆弧能够同时满足最大轮廓误差和小线段长度2 个约束，这里分成2 种情况进行讨论，以确定过渡圆弧的半径r 和圆弧的接入点Q0及转出点Q2.

1)当lc≤ls时，表明由最大轮廓误差确定的过渡距离能够同时满足小线段自身长度的要求，因此过渡圆弧的参数仅根据最大轮廓误差得出即可.此时过渡距离为lc，根据式(3)和几何上的比例关系可以计算出过渡圆弧的半径r 和圆弧的接入点Q0及转出点Q2，它们分别为，

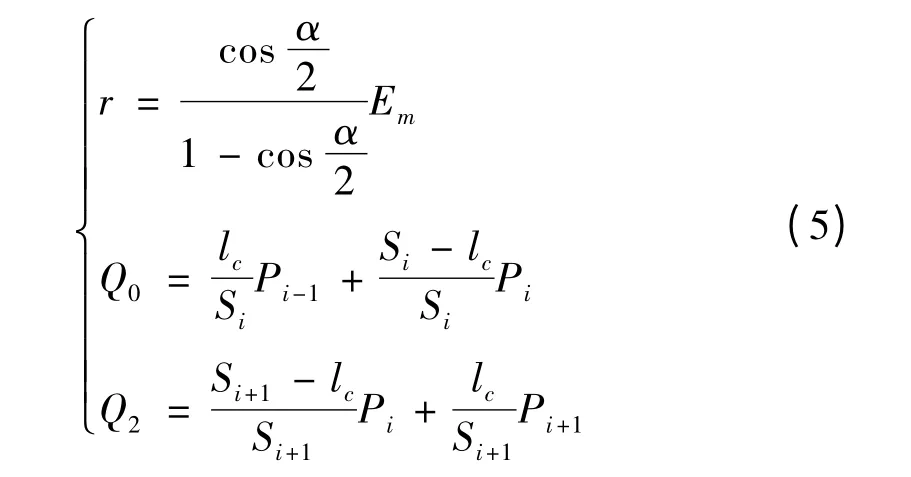
2)当lc＞ls时，表明由最大轮廓确定的过渡距离不能够满足小于小线段自身长度一半的要求，因此还应该由小线段长度进一步约束过渡圆弧的参数.此时的过渡距离为ls，同理，根据几何上的比例关系可以计算出过渡圆弧的半径r 和圆弧的接入点Q0及转出点Q2，它们分别为，

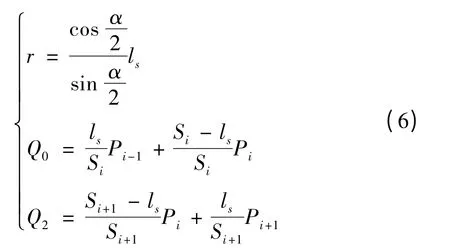
首先根据最大轮廓精度和小线段长度算出由它们分别决定的过渡距离，比较lc和ls根据情况将其一和线段端点Pi－1、Pi、Pi+1代入式(5)或(6)中就可以得到唯一的满足最大轮廓误差和小线段长度2 个条件的过渡圆弧.

2.2 过渡圆弧旋转方向的确定

圆弧插补有2 种描述方法:半径描述方法和圆心坐标描述方法.本研究的过渡圆弧采用的是半径描述的方法，除了确定圆弧的起始坐标、终点坐标和半径外，还需要判断其是顺时针或逆时针方向.在向量的叉乘中，2 个向量的向量积方向同样符合右手定则，因此本研究将一系列小线段所在的平面坐标系扩充为三维坐标系，即原来小线段所在的xOy 面保持不变，作垂直于该坐标平面的轴为z 轴，然后以相邻小线段为向量，研究它们的向量积方向就可以判断出相邻小线段间过渡圆弧的旋转方向.

假设有如图1 的相邻小线段，且Pi－1、Pi、Pi+1的坐标分别为(xi－1，yi－1)、(xi，yi)、(xi+1，yi+1)，将平面坐标系扩充为三维坐标系后，由于小线段处于xOy面上，因此Pi－1、Pi、Pi+1在三维坐标系中的坐标为(xi－1，yi－1，0)、(xi，yi，0)、(xi+1，yi+1，0)，则 向 量分别表示为(xi－ xi－1，yi－ yi－1，0)、(xi+1－ xi，yi+1－ yi，0).设根据向量积的坐标表达式，

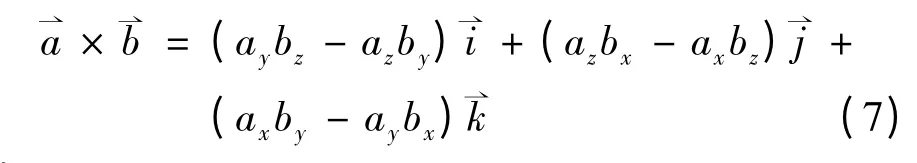
可知，

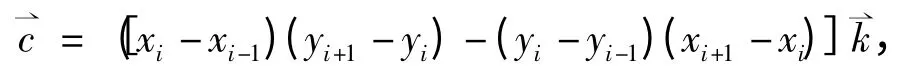
2.3 过渡圆弧段最大进给速度的确定

直线段的插补按照设定的最大进给速度工作，受到工作平台机械特性的约束，其所能提供的最大加速度是有限的.为了保证加工过渡圆弧时的法向加速度满足加工平台的机械特性，需要限定过渡圆弧段的最大进给速度.假设加工平台所能提供的最大加速度为am，过渡圆弧的半径为r，则根据向心加速度公式得出由最大加速度所限制的过渡圆弧段的最大进给速度vm为，

为了使过渡圆弧既能符合加工工艺的要求，又能满足加工平台机械特性，最终过渡圆弧段的最大进给速度应取系统设定最大速度、最大加速度限制的进给速度vm中的最小值，即，

在进入到过渡圆弧段之前，应当提前进行减速，使加工速度在过渡圆弧的接入点时恰好为v，并以该速度完成过渡圆弧的加工.

2.4 离线的前瞻控制

一般意义上的前瞻控制是实时的，若本研究算法采用实时前瞻控制实现，那么控制器应当先由用户对加工图形进行编程，用直线插补指令对分解出来的一系列小线段进行直线插补.当使用前瞻控制功能时，控制器从用户编写的指令中预先获取待加工路径的几何信息，提前计算出各个相邻小线段拐角处过渡圆弧的参数和最大进给速度，并插入到相应的拐角中，然后按照平滑后的加工路径进行加工，如图4 所示.

图4 平滑后的加工路径

本研究采用固高GTS-400-PV 运动控制卡对算法进行验证，因此无法对其进行前瞻控制，只能采用离线的方式完成前瞻控制功能并用控制卡自身的指令实现.对此，本研究使用VC 6.0 作为开发工具，编写程序完成前瞻控制的运算并产生相应的代码.首先将原始路径上各个端点的数据保存于文本文档中，并与该程序存放于相同目录下，运行程序后自动读取文档中的数据，再根据这些数据和程序中设定好的诸如最大加速度、进给速度等加工参数自动计算各个拐角处过渡圆弧的参数以及每个过渡圆弧段的最大进给速度，最后将计算出来的结果按照该型号控制卡直线插补和圆弧插补的指令格式输出至新的文本文档中，将指令复制到控制卡的程序代码中，即可完成前瞻控制的功能.

3 实验验证

在工件的小线段加工中，加工效率的高低主要取决于各个拐角点所允许的最大进给速度.本研究采用固高GTS-400-PV 运动控制卡进行验证.在进给速度F = 20 pulse/ms，最大加速度am= 0.15 pulse/ms2，最大轮廓误差Em= 1 pulse 的条件下，分别采用直接过渡的方式和本研究算法对如图5 的图形进行加工，图中一端为原点的斜线为图形加工前的过渡段，计入整个加工过程，并实际测试它们的加工时间和加工时的速度曲线，结果如图6、7 所示.

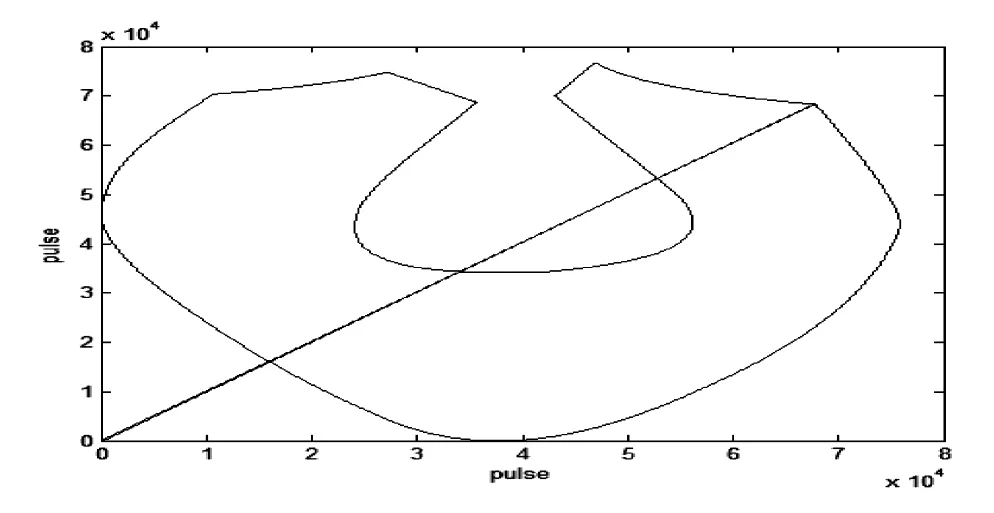
图5 工件加工图形

图6 直接过渡方法的速度曲线

图7 本研究算法的速度曲线

图6、7 显示，采用直接过渡的方式进行加工的时间为29 063 ms，而采用本研究算法进行加工的时间为25 250 ms.相比于直接过渡的方式，本研究算法对加工效率的提升为13.12%.同时，从加工时的速度曲线来看，直接过渡的方式在各个拐角点处仍保持一定的进给速度，其加减速频率明显降低，整体速度有了大幅提高，但采用本研究算法时的速度曲线相比于直接过渡方法更为平滑，加减速频率进一步降低，且平均速度也有了一定的提高，有效提升了加工效率.

4 结 论

本研究在分析现有小线段平滑过渡算法的基础上，根据一般控制器的需求，首先建立过渡圆弧的数学模型，并以此推导基于过渡圆弧的小线段平滑过渡算法，最后采用固高GTS-400-PV 运动控制卡进行测试.通过与控制卡前瞻控制模块所使用的直接过渡方式进行对比，可以看出该算法过渡平滑并实现简单的特点，能够在不影响加工质量的条件下有效地提升小线段加工的效率.

［1］叶伟，王小椿.一种连续小线段高速插补算法［J］.南京理工大学学报(自然科学版)，2008，32(4):443－448.

［2］张得礼，周来水.数控加工运动的平滑处理［J］.航空学报，2006，27(1):125－130.

［3］冷洪滨，邬义杰，潘晓弘.三次多项式型微段高速自适应前瞻插补方法［J］.机械工程学报，2009，45(6):73－79.

［4］沈斌，齐党进，樊留群，朱志浩.基于NURBS 曲线拟合的微段高速自适应加工算法［J］.中国机械工程，2012，24(15):1825－1829.

［5］何均，游有鹏，王化明.面向微线段高速加工的Ferguson样条过渡算法［J］.中国机械工程，2008，19(17):2085－2089.

［6］李方，李迪，黄昕.非均匀有理B 样条在线拟合高速平滑插补法［J］.华南理工大学学报(自然科学版)，2010，38(8):61－65.