一种改进的最大信杂比MTD滤波器设计算法
贾可新 张锦中
(华东电子工程研究所 合肥 230088)
一种改进的最大信杂比MTD滤波器设计算法
贾可新 张锦中
(华东电子工程研究所 合肥 230088)
为了提高算法对调节因子和初始阻带衰减的稳定性,提出了一种改进的最大信杂比MTD滤波器设计算法。与原始的设计算法相比,该算法通过对滤波器频响与期望频响的误差进行归一化处理,并重新计算某些杂波功率为零,但不满足期望阻带衰减要求的频点的杂波功率,获得了改进的杂波功率迭代公式,降低了对调节因子的敏感性。为降低初始阻带衰减对算法稳定性的影响,所提算法采用了逐次增大初始阻带衰减的策略。因此,改进的MTD滤波器设计算法不需反复调节控制参数,提高了设计效率,具有较高的价值。仿真实例验证了所提算法的有效性。
MTD滤波器组;杂波抑制;最大信杂比准则;脉冲重复频率
Abstract: To improve algorithm stability for regulatory factor and initial stopband attenuation, a design algorithm of modified maximum signal-to-clutter ratio(SCR) moving target detection (MTD) filters is presented. Comparing with original design algorithm, using this algorithm can achieve improved clutter power iterative formula, and reduce sensitivity to regulatory factor by normalized processing error between filter frequency response and expected frequency response and recalculating clutter power of frequency point whose power is zero, but it cannot meet requirement for expected stopband attenuation. In order to reduce effect of initial stopband attenuation on algorithm stability, the proposed algorithm employs strategy of increasing initial stopband attenuation gradually. Hence, the modified MTD filter design algorithm does not need to regulate control parameters so as to increase design efficiency. It provides higher value. The simulated example verifies effectiveness of the presented algorithm.
Key-words:MTD filter bank; clutter suppression; maximum signal-to-clutter ratio criteria; pulse repetition frequency
0 前言
在工作环境中,雷达接收信号不但含有来自运动目标的回波信号,也有从地物、云雨以及人为施放的箔条等物体散射产生的杂波信号。由于杂波往往比目标信号强得多,杂波的存在会严重影响雷达对运动目标的检测能力。因此,自适应杂波抑制是雷达信号处理的重要内容[1-4]。
在自适应杂波抑制方法中,动目标检测(MTD)是一种利用多普勒滤波器来抑制各种杂波,以提高雷达在杂波背景下检测运动目标能力的技术[1-4]。目前,MTD滤波器组常采用FFT滤波器组或有限脉冲响应(FIR)滤波器组实现。与FFT滤波器组相比,FIR滤波器组中某些滤波器的(幅度)频率响应能够在零频附近灵活的形成较深的零陷,用于抑制零频附近杂波。
为了灵活形成零频附近的零陷,文献[5]将阵列方向图数字综合算法[6]和常规自适应滤波器相结合,给出了一种MTD滤波器设计算法,它假设杂波具有高斯型功率谱,且需已知杂波的协方差矩阵。文献[8]借鉴文献[6,7]中阵列综合的思想,提出了一种基于最大信杂比准则的MTD滤波器设计算法,该方法虽无需杂波功率谱,通过迭代更新杂波功率,获得满足最大信杂比准则的最佳滤波器系,但对调节因子和初始阻带衰减值比较敏感,若参数选择不当,容易不收敛。
为提高文献[8]中算法的稳健性,降低其对调节因子和初始阻带衰减值的依赖性,本文借鉴文献[9]和[10]中阵列方向图数字综合的思想,提出了一种改进的MTD滤波器设计算法。该算法无需反复调节控制参数,提高了滤波器设计的效率。
1 原始的MTD滤波器设计算法
原始的MTD滤波器设计算法是一种基于最大信杂比准则的迭代设计算法。该算法的原理为:假设在重频范围内,均匀分布着许多窄带杂波,通过调节各窄带杂波的功率,使得滤波器在满足期望阻带衰减的同时,获得最大的输出信杂比。
设MTD滤波器的期望阻带衰减为D(ω)dB,相应的实际值为d(ω)=10D(ω)/20。若令系统噪声为白噪声,M个窄带杂波均匀分布在整个重频范围内,其在通带内的功率固定为0。因此,杂波和噪声的自相关矩阵为
(1)
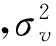
对于滤波器的通带,不允许引入窄带杂波,当窄带杂波位于滤波器通带内时,令其功率为零。因在每次调节杂波功率时,滤波器通带宽度会发生变化,故需要在每次调节时,重新确定通带范围,即确定频谱第一零点ωL、ωH的位置。对于滤波器的阻带,当阻带范围内某个频点ωm处的衰减G(ωm)大于期望的阻带衰减d(ωm)时,增加该频点处的杂波功率;反之,减小该频点处的杂波功率。在调节各频点杂波功率时,窄带杂波功率不能为负数,若在调节过程中,得到的阻带区域内杂波功率为负,则令其等于零。
若第k次迭代得到的滤波器频谱为G(ωm,k),相应的通带范围内的最大值为Gmax(k),则在第k次迭代过程中,第m个频率处的期望幅度值为

(2)
其中,d(ωm)为第m个频率处的期望衰减值。因此,窄带杂波功率由第k次到第k+1次调节时的更新公式
(3)
Γm(k)=ξm(k)+η[G(ωm,k)-rm(k)]
(4)
其中η为调节因子。第k次调节的滤波器系数为
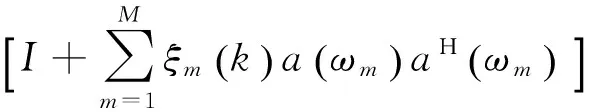
(5)
通过不断调节杂波功率,使得滤波器的频谱满足期望的阻带衰减,最后一次调节对应的自适应权向量即为所求的最佳滤波器系数。
2 改进的MTD滤波器设计算法
在原始的MTD滤波器算法中,调节因子η的选择受滤波器中心频率的影响比较大。对于给定的滤波器中心频率,调节因子η若选择不合适,将导致算法不收敛。对于滤波器加权系数的初始值选择,为了在零频附近形成零陷,要求该权值对应的阻带衰减略大于期望阻带衰减。当滤波器的初始阻带衰减值选择不合适时,算法将不收敛。为获得一个合适的调节因子和初始阻带衰减值,在实际使用时需要人工反复调节,降低了设计MTD滤波器的效率。
为了降低滤波器系数初始值和调节因子η对算法收敛性能的影响,提高算法稳定性,本节给出一种改进的MTD滤波器设计算法。由式可知,在某一次迭代中,某一频率的杂波功率为零,则该频率处的杂波功率在以后的迭代中一直为零。这必将影响算法的收敛性,因杂波功率为零的频率处的阻带衰减值并不一定满足期望衰减要求。因此,本文将修正窄带杂波功率由第k次到第k+1次迭代时的迭代公式。
令Δm(k)=G(ωm,k)-rm(k),则由第k次到第k+1次迭代时的公式可更新为
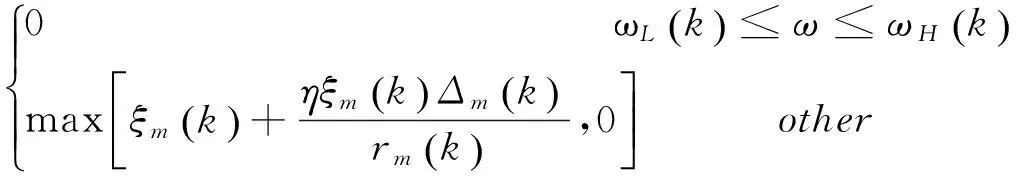
(6)
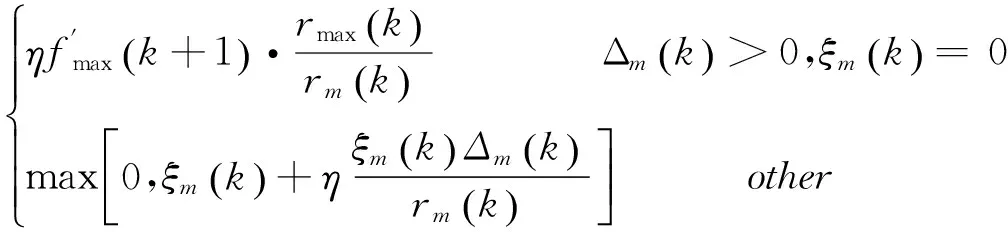
(7)
(8)
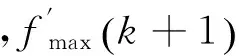
为改善滤波器初始阻带衰减值对算法收敛性的影响,本文给出了一种逐次增大初始阻带衰减值的方法,即给定一个略大于期望阻带衰减值的初始值,经多次迭代后,若算法不收敛,则按固定步进增大滤波器的初始阻带衰减值。如此反复调整,直到算法收敛。
基于以上讨论,改进的最大信杂比MTD滤波器组的设计步骤可总结如下:
1)给定某个滤波器的中心频率ω0,设置期望阻带衰减d(ω)=10D(ω)/20,初始化窄带杂波功率ξm(0)=0,m=1,2,…,M。
2)根据滤波器的初始阻带衰减值,调整滤波器系数的加权系数,计算滤波器的初始通带范围ωL(k),ωH(k)。
3)根据式(6)、(7)和(8),迭代调节窄带杂波功率,根据式(5)计算最佳滤波器系数,确定滤波器的通带范围ωL(k+1),ωH(k+1)。
4)比较滤波器的实际阻带衰减与期望阻带衰减,若满足要求,则停止;若不满足最大迭代次数则重复执行步骤3;若满足最大迭代次数,则执行步骤5。
5)按固定步进增加滤波器初始阻带衰减值,重复执行步骤2到步骤4,直到满足期望阻带衰减要求。
3 仿真实验
本节将通过仿真实验验证所提算法的有效性。设MTD滤波器的阶数为12,滤波器总个数为13,零频附近四个滤波器的阻带衰减-35dB,剩余九个滤波器的阻带阻带衰减-35dB,在零频附近归一化频率宽度0.05内零陷深度低于-60dB。窄带杂波个数取为128,迭代次数100。本实验仅考虑需在零频附近形成零陷的某些滤波器的设计。
采用原始MTD滤波设计算法,取归一化中心频率等于0.2283,调节因子为1,当滤波器系数初始阻带衰减值为-37dB,经100次迭代,其频率响应如图1(a)所示,所设计的滤波器不满足期望频率响应要求。当初始阻带衰减值为-42dB时,其频率响应如图1(b)所示,所设计滤波器在零频附近不满足期望频响要求,该的加权损失为1.3266dB,它虽在频率范围[0.4,0.8]内衰减值满足期望频率响应要求,但比期望值小约3dB,这将增加滤波器的加权损失。当初始阻带衰减值为-42dB时,将调节因子改为0.01,其频率响应如图1(c)所示,该滤波器的加权损失为1.3199dB,满足期望频率响应要求。维持阻带衰减值和调节因子不变,将归一化中心频率改为0.45,其频率响应如图1(d)所示,所设计滤波器的加权损失为1.347dB,它虽满足期望频响要求,但在阻带范围内比期望值小约5dB,这同样增加了滤波器的加权损失。由图1可知,原始MTD滤波器设计算法对调节因子和初始阻带衰减值比较敏感。若相关参数选择不合适,将可能使算法不收敛,即使算法收敛,其加权损失也较大。
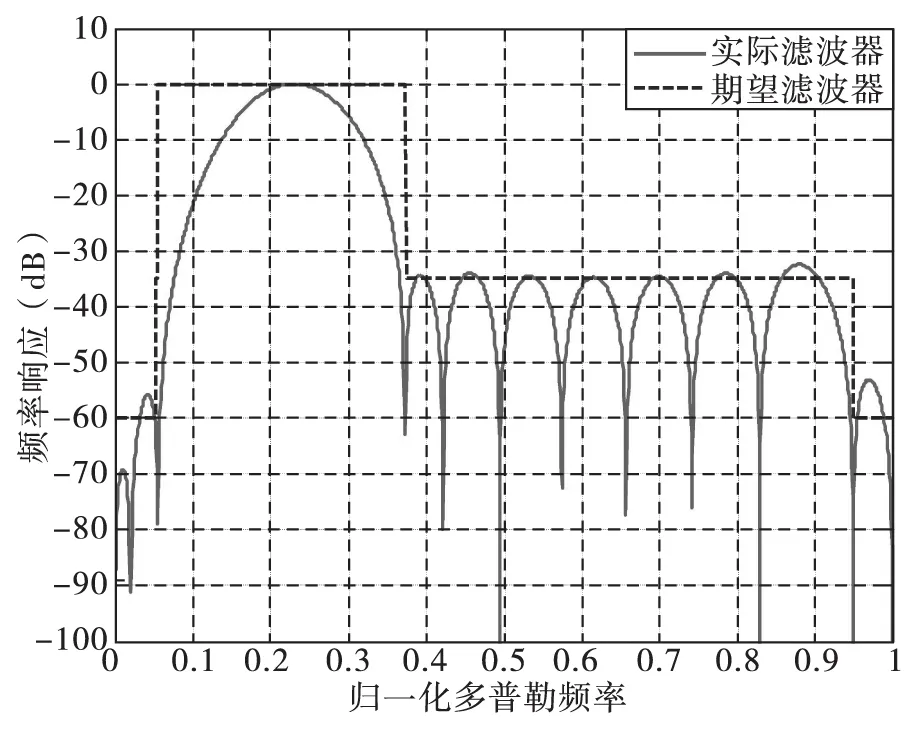
(a) 初始阻带衰减-37dB,调节因子为1,中心频率0.2283
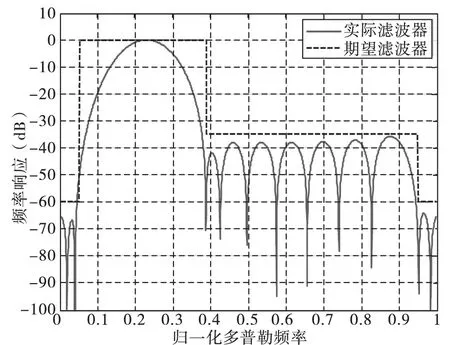
(b) 初始阻带衰减-42dB,调节因子为1,中心频率0.2283
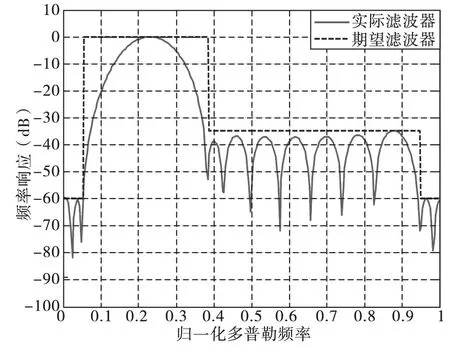
(c) 初始阻带衰减-42dB,调节因子为0.01,中心频率0.2283

(d) 初始阻带衰减-42dB,调节因子为0.01,中心频率0.45
采用改进MTD滤波设计算法,取归一化中心频率等于0.2283,调节因子为1,当滤波器系数初始阻带衰减值为-37dB,逐次增加衰减值的步进为1dB,经100次迭代,其频率响应如图2(a)所示,该滤波器满足期望频率响应要求,加权损失为1.2617dB。维持调节因子和初始阻带衰减不变,将归一化中心频率改为0.45,其频率响应如图2(b)所示,该滤波器满足要求,其加权损失为1.1421dB。由图2可知,所提改进算法对调节因子和初始阻带衰减值不敏感,在满足要求的前提下,使加权损失最小。
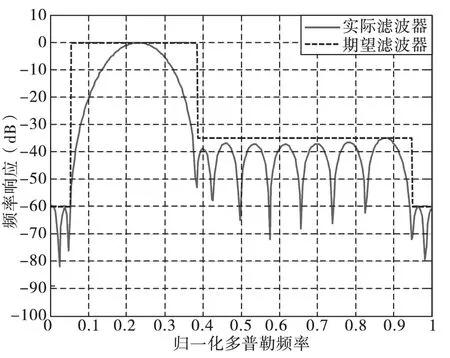
(a)归一化中心频率为0.2283

(b)归一化中心频率为0.45
4 结论
为改善滤波器设计算法的收敛性能,本文提出了一种改进的MTD滤波器设计算法。所提算法充分考虑了在迭代过程出现某些频点杂波功率为零,但不满足期望阻带衰减要求的情况,并给出了相应的迭代公式。这一改进降低了算法对调节因子的依赖性,提高了算法收敛性能。同时为改善滤波器初始阻带衰减值对算法收敛性的影响,在所提算法中采用了逐次增大初始阻带衰减值的策略。与原始MTD算法相比,所提算法对调节因子和初始阻带衰减值不敏感,不需要通过多次实验人工选择合适参数,提高了MTD滤波器设计的效率。
[1] 吴顺君,梅晓春. 雷达信号处理和数据处理技术[M]. 北京:电子工业出版社,2008:105-146.
[2] L. J. Spafford. Optimum radar signal in clutter[J].IEEE Trans. Information Theory,1968,14(6):734-743.
[3] 陈小龙,关键,郭海燕,黄勇. 基于WPT-FRFT的微弱动目标检测及性能分析[J]. 雷达科学与技术,2010,8(2):139-145.
[4] E. D’addiio.Performance comparison of optimum and conventional MTI and Doppler processors [J]. IEEE Trans. Aerospace and Electronic Systems,1984,20(6):707-714.
[5] 谷泓,赵永波,张守宏. 一种基于数字综合算法的MTD滤波器设计方法[J]. 航空计算技术,2002,32(2):58-62.
Gu Hong,Zhao Yongbo,Zhang Shouhong. A design method of MTD filters based on the numerical synthesis algorithm[J].Aeronautical Computer Technique,2002,32(2):58-62.
[6] Carl A. Olen,R. T. Compton. A numerical pattern synthesis algorithm for arrays[J]. IEEE transactions on antennas and propagation,1990,38(10):1666-1676.
[7] 王永良,丁前军,李荣锋. 自适应阵列处理[M]. 北京:清华大学出版社,2009:220-271.
[8] 贾可新,柳桃荣.一种基于最大信杂比的MTD滤波器设计算法[J]. 雷达科学与技术,2014,12(5):506-509.
[9] Guo Q H,Liao G S,Wu Y T. Pattern synthesis method for arbitrary arrays based on LCMV criterion. Electronics Letters,2003,39(23):1628-1630.
[10] Liu Jun,Liu Zheng,Qi Fei-lin.Sum and Difference pattern synthesis for conformal arrays.
AnAlgorithmofDesigningModifiedMaximumSignal-to-ClutterRatioMTDFilterBank
Jia Kexin, Zhang Jinzhong
( East China Research Institute of Electronic Engineering, Hefei 230088)
TN958.2
A
1008-8652(2017)02-047-05
2017-03-13
贾可新(1982-),男,工程师。主要研究方向为雷达和对抗领域信号处理。

