偏置自纠错最小和译码算法

周志伟，孙发鱼，白瑞青

(西安机电信息技术研究所，陕西 西安 710065)

0 引言

信道编码是为了克服信息在信道传输过程中受到干扰和噪声，保证通信系统的传输可靠性而设计的一类抗干扰的技术。目前PCM/FM遥测系统中较多采用的是多符号检测和Turbo乘积码技术[1-2]。相比于Turbo码，LDPC码有更加优异的译码性能，低的译码复杂度和高度并行化带来较短的译码时延，在高码率时的优势更加明显[3]。好的译码算法应该可以在保证性能的基础上降低译码的复杂度。目前LDPC译码主要采用置信传播译码，通过该译码算法可以得到与最大似然译码一样优异的性能，但是也导致算法的复杂度过高，尤其在码长过长时，译码的复杂度往往随着码长的增加呈指数型增长。为了降低译码的复杂度，研究人员对其进行了深入的探索与改进，之后提出了最小和译码算法，该算法是将对数似然比算法中的对数运算简化为比较运算，极大地降低了译码复杂度，但是性能上带来了一定的损失[4]。针对置信传播译码复杂度高以及最小和算法性能不佳的问题，本文提出偏置自纠错最小和译码算法。

1 LDPC码译码算法

1.1 LDPC表示方法

LDPC码是一种(n,k)线性分组码，其中码长为n，信息序列长度为k，由m×(n-k)校验矩阵H唯一决定。H的每一个列向量对应一个码字，每一个行向量对应一个校验方程[5]。 其中LDPC码校验矩阵H包含大量的零元素，只有少量的非零元素，这种稀疏特性大大降低了译码复杂度。

一般校验矩阵H以矩阵和Tanner图两种形式来表示，下面给出了一个5行10列行重为4列重为2的校验方程和校验矩阵。

(1)

(2)

该LDPC码Tanner图如图1所示，图中a为校验节点,b为变量节点。通过Tanner图可以直观地展现迭代译码的过程。可以看出,Tanner图是双向图,可以用G={(V,E)}表示，其中V表示节点的集合，V=Va∪Vb。若校验矩阵H维度为m×n，则变量节点数量有n个，以Vb=(b1b2…bn)表示,每个Vb中元素对应H的一列或一个码字。校验节点数量有m个,以Va=(a1a2…an)表示,每个Va中元素对应一行。所有边的集合用E属于Vb∪Va来表示,同种节点间无相连边。校验矩阵每有一个非零元素,校验节点和变量节点间就会存在一条边进行连接。

图1 Tanner图Fig.1 Tanner

1.2 LDPC译码

译码算法的选取直接决定了是否能激发出码本身具有的潜在优势，特别是在译较长码的时候，译码复杂度往往伴随码长的增加呈指数型增长，因此选取好的译码算法可以在保证性能的基础上减小译码的复杂度，易于硬件实现[6]。

LDPC码有很多种译码方法，本质上都是基于Tanner图的消息迭代译码算法。

置信传播译码是根据软迭代信息进行概率译码，每一轮迭代都需要对码字中的各个码字关于接收码字和信道参数的后验概率进行估算，因此置信传播译码算法是一种逐比特最大后验概率算法，所有迭代过程可以看作有校验矩阵决定的Tanner图上进行消息传递的过程[7]。在讨论算法前，先介绍算法符号代表的含义：

a∈{1,2,3，…，M}，校验矩阵的第a个校验节点；

v∈{1,2,3，…，N}，校验矩阵的第v个变量节点；

s表示算法的迭代次数；

S(s)(Qv)迭代次数为s时第v个变量的后验概率；

M(a)表示与校验节点a连接的变量节点的集合；

N(v)表示与变量节点v连接的校验节点的集合；

a′∈M(a)/v表示与第a个校验节点相连的除去第v个变量节点的其他变量节点的集合；

v′∈N(v)/a表示与第v个变量节点相连的除去第a个校验节点的其他变量节点的集合；

S(s)(Ra，v)在第s次迭代过程中，由第a个校验节点传递给第v个变量节点的信息；

S(s)(Qv，a)在第s次迭代过程中，由第v个变量节点传递给第a个校验节点的信息。

1.2.1 置信传播算法

设编码器输出的码字为ci，在AWGN信道下进行BPSK，输出为xi(xi=2ci-1)；经过信道后，译码器接收变量为yi，其中yi=xi+n，n服从高斯分布N(0，σ2)。

1) 初始化

根据接收变量yi，来计算ci=1的条件概率：

令P(xi=1)=P(xi=-1)=1/2，则：

从定义可知，Pv1是接收变量yi得到关于ci=1的消息。

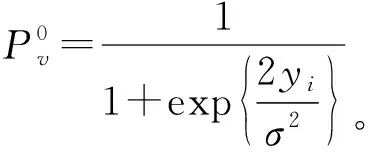
根据校验矩阵H，若hij=1,则变量节点vi与校验节点ai连接，定义变量消息：

迭代过程主要由两个更新步骤组成，执行迭代这两个步骤，对每一比特的后验概率进行准确的估算。

2) 校验节点更新：对变量消息进行计算得到新的校验消息。

在二进制M维序列中，如果任意的一位ai(i=1,2,3，…，M)的概率为P(ai=1)=Pi，则该序列中含有偶数个1的概率为：

含有奇数个1的概率为：

3) 变量节点更新：对校验消息进行计算得到新的变量消息。

(1)

4) 译码判决

每一轮迭代完成后，对每个信息比特xi(i=1,2,3，…，n)计算其后验概率：

最后可以得出对发送码字的一个估计c′=[c1,c2,c3,…,cn]。计算其伴随式S=cHT,如果S=0，则译码成功，结束其迭代；否则继续迭代，若迭代次数达到预先设定的最大值仍未成功，则失败，结束迭代。

1.2.2 最小和算法

置信传播算法中含有大量的乘除运算，不利于硬件实现，对于硬件开发而言，实现乘法运算消耗的资源比加法运算和比较运算大的多，时延大。除此之外，在实际应用中，由于噪声方差σ2需要通过信道估计获取的准确度没有办法保证，所以迭代信息不易获取，因此提出了最小和译码算法[8]。

1) 初始化

将初始信道信息传递给变量节点作为初始信息：

2) 校验节点更新

3) 变量节点更新

4) 计算后验概率

5) 译码判决

该算法在校验节点的更新中运用了符号运算与比较运算代替了乘积运算，极大地降低了运算的复杂度，并且在迭代中使用的初始信息2yi/σ2简化为yi，极大地减小了获取信息的复杂度。但是由于最小和算法是对校验节点更新的简化，因此降低译码复杂度的同时也使译码性能下降，本文提出偏置自纠错最小和译码算法，引进在校验节点的更新过程中加入偏置系数α，同时改变其变量节点的更新过程，删除变量节点更新过程中的不可靠信息。

2 偏置自纠错最小和算法

1) 初始化

将初始信道信息传递给变量节点作为初始信息：

2) 校验节点更新

3) 计算后验概率

4) 变量节点更新

L(l)(Qa,v)=

6) 译码判决

偏置自纠错算法通过在校验节点的更新过程中引入偏置系数，弥补了最小和算法近似运算带来的损失，同时改变其变量节点更新过程，在连续两次迭代中，如果变量节点更新结果符号相异，就把变量节点的更新结果取零，删除了变量节点更新过程中的不确定信息，使译码性能得到提高。这种算法只是增加了加法运算与比较运算，相比于传统的置信传播算法的乘积运算的复杂程度可以忽略不计，更加容易硬件实现。相比于最小和算法，只是加入一点代价就极大提高译码的性能。

3 算法仿真

3.1 算法复杂度分析

表1列出了置信传播算法、最小和算法、偏置自纠错算法3种算法节点更新所需要的乘法、加法、比较及其他运算的次数，其中da表示校验节点的度，dv表示变量节点的度。

偏置自纠错最小和算法存在加法运算、比较运算以及极少数的乘法运算，而置信传播算法中存在着大量的乘法运算，随着码长的增加，其计算复杂度呈指数型增加。相对于置信传播算法，偏置自纠错算法大大节省了计算量，更容易硬件实现，同时相比于最小和算法，本文提出的偏置自纠错算法在只增加加法运算及比较运算的前提下，极大地提高了译码性能。

表1 算法次数Tab.1 Number of algorithms

3.2 仿真结果及分析

偏置自纠错算法中的偏置因子α，是影响译码性能的关键因数之一，若是偏置因子选取合适，则可以使偏置自纠错算法在性能上逼近置信传播算法。本文给出了4种偏置因子α的性能曲线，如图2所示。

图2 偏置自纠错最小和算法在不同偏置系数下的性能Fig.2 The performance of the bias selfcorrecting minimum sum algorithm under different bias coefficients

从图2可以得到，当偏置系数α=0.1 时，该算法译码性能最佳，同时在硬件实现上比较简单，只需通过加法器与比较器就可以实现。通过以上分析，本文选取α=0.1 为该算法的偏置因子。

为了充分衡量偏置自纠错最小和译码的性能，在AWGN信道下，采用了BPSK调试的方式，分别对硬判决、置信传播、最小和以及本文所提出的偏置自纠错最小和译码算法进行了仿真分析。LDPC码采用码长为1 024的规则码，码率为1/2，最大迭代次数为30次。

图3给出了不同译码算法的误码率与信噪比曲线的仿真结果图。通过曲线可以看出置信传播算法的性能最好，硬判决译码的性能最差，当误码率为10-5时，置信传播算法与偏置自纠错算法算法相比有0.1 dB的增益，但是置信传播算法的译码复杂度相比于偏置自纠错算法要高，随着码长的增加和迭代次数的变大，译码复杂度会越来越高。同时由于最小和算法采用了近似的方法损失了部分的性能，偏置自纠错算法引入偏置因子，改变了变量节点的更新过程，删除了变量节点更新过程中的不可靠信息，弥补了最小和算法带来的损耗，使其性能逼近置信传播算法。

图3 不同译码算法性能比较Fig.3 Performance comparison of different decoding algorithms

4 结论

本文提出偏置自纠错最小和译码算法，该算法的主要思想是通过添加偏置系数，改变其变量节点的更新过程，删除变量节点更新过程中的不可靠信息，弥补了最小和算法由于近似运算带来的损耗，使其性能逼近置信传播算法。仿真结果表明，本文提出的偏置自纠错最小和算法，相较于置信传播算法，运算复杂度降低，拥有较小的时延，性能优于最小和算法，易于硬件实现，具有一定的研究和应用价值。

虽然初步完成所需工作，但是如何找出适用于偏置自纠错最小和译码算法的最优性能参数，还需要做大量工作。