聚四氟乙烯材质引信天线罩烧蚀算法

魏 新，纪 涛，刘忙龙

(西安机电信息技术研究所，陕西 西安 710065)

0 引言

随着远程火箭弹的射程不断增加，飞行速度也越来越快，在高速气流下气动热产生的烧蚀也越来越严重。引信天线罩位于火箭弹的头部，受到的气动热环境最为恶劣，因此天线罩的气动热烧蚀问题的研究显得尤为重要。目前烧蚀计算的工程算法根据材料特性分为三种：硅基复合材料工程算法、碳基复合材料工程算法和碳化复合材料的工程算法，这些工程算法已被广泛研究。文献[1]中基于碳/碳材料的热化学烧蚀模型推导出C/C/Al2O3材料的烧蚀公式，并研究了烧蚀规律。文献[2]中研究了碳化锆材料的烧蚀机理，给出了材料原始层的表面可能存在的化学反应，建立了材料的烧蚀响应数学模型。文献[3]对酚醛浸渍多孔碳纤维复合材料进行了氧乙炔烧蚀试验，并对烧蚀行为进行了有限元模拟，得出材料的烧蚀规律。文献[4]采用气动热化学烧蚀机理，扩散和化学动力机制，计入气流与粒子的侵蚀，建立了三元乙丙橡胶的烧蚀模型。这些材料已在航天航空领域广泛应用，而在火箭弹上天线罩普遍采用的材料为聚四氟乙烯。聚四氟乙烯材料的烧蚀计算按照碳基复合材料的烧蚀算法，目前国内外学者对聚四氟乙烯烧蚀过程的化学反应一般采用19组元28种反应模型[5]和19组元29种反应模型[6]。这些模型包含的组元数和反应方程较多，在实际的工程应用中比较困难。为此，本文提出了简化的聚四氟乙烯材质引信天线罩烧蚀算法。

1 碳基复合材料烧蚀计算理论

飞行器烧蚀热防护计算是以高超声速化学边界层理论为基础。假定气流为定常、二维或轴对称，有m个组元的混合气体边界层，其基本方程如下：

总连续方程：

(1)

组元连续方程：

(2)

式(2)中，ci为i组元质量浓度，ωi为单位时间、单位体积内由于化学反应而生成的i组元质量。

采用局部平衡假定时，壁面温度为未知量ωi采用独立组元的概念，确定局部化学平衡条件下各组元质量浓度。设m个组元的分子式共含有σ个元素，i组元的化学分子式Ai可写成：

(3)

则有：

(4)

式(4)中，vij为化学计量系数，{Aj}为独立组元，{Ai}为{Aj}的混合物，由式(1)—式(4)可得j种组元的当量质量浓度为：

(5)

(6)

(7)

得到当量质量浓度的微分方程：

(8)

在化学边界层中，以当量质量浓度边界条件代替质量分数边界条件为：

简化计算，假定Le=Pr=Sc=1，此时状态方程和扩散方程为：

(9)

(10)

则有：

(11)

对式(1)—式(8)进行积分，可以得到：

(12)

则有：

(13)

式(13)中，st为壁面热交换系数。

2 聚四氟乙烯材料的烧蚀算法

碳基复合材料烧蚀机理由两部分组成，即热化学烧蚀和机械烧蚀。通常对烧蚀的计算主要以计算化学烧蚀的质量损失率来确定。本文是以碳基复合材料烧蚀机理的计算方法为基础，建立了聚四氟乙烯材料的烧蚀计算模型并进行了计算。聚四氟乙烯材料的烧蚀壁面边界和碳/碳材料类似，聚四氟乙烯属于低温烧蚀材料，在烧蚀过程中的反应主要产物为C2F4，烧蚀表面的主要化学反应为：

(14)

由上式可得平衡常数分别为：

(15)

式(15)中，K为化学平衡常数，组元分压有10个，方程组不封闭，因此需要根据相容性条件补充关系式，引进质量浓度ci，由状态方程(11)导出ci与组元分压的关系为：

(16)

(17)

(18)

(19)

在Le=Pr=1的条件下，引入无因次质量损失率B，由相容性条件得：

(20)

(21)

(22)

由于表面温度可由热传导方程决定，其进入壁面的静热流，可由表面能量平衡关系确定，表面能量平衡关系如图1所示。

图1 烧蚀表面能量示意图Fig.1 Energy schematic diagram of the ablation surface

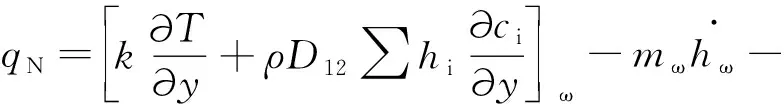
(23)

式(23)中各未知量均可以看作是温度和压力的函数，根据热环境的计算结果确定表面热流，进一步求得无因次质量损失率B，进而可求得材料的质量损失率。

则材料的烧蚀性能通过材料的烧蚀率表征为：

(24)

式(24)中，ρ为固体材料密度。

3 算例及验证

3.1 算例

根据引信体外形尺寸建立仿真模型进行计算，在高速气流作用下，烧蚀最为严重的过程发生在火箭弹前端，为了便于简化模型，本文主要针对头部位置的引信天线罩进行建模，计算模型如图2所示。

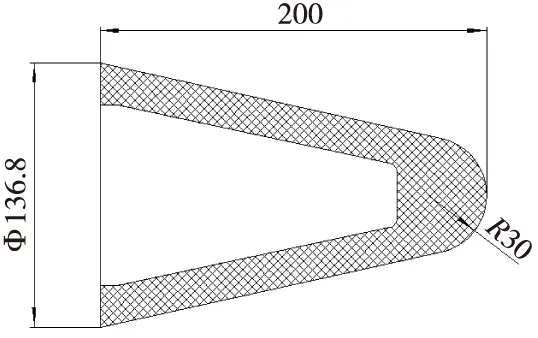
图2 引信天线罩结构示意图Fig.2 Dagram of the fuse radome structure

天线罩材料为聚四氟乙烯，密度2.2×103kg/m3，比热容1.05 kJ/kg·K，热传导系数0.3 W/m·K。选取火箭弹小射程的弹道参数作为算例条件，小射程最大速度为2 000 m/s,飞行时长为120 s。由飞行速度和时间得到引信天线罩的气动热环境参数，热环境参数见表1。

表1 引信天线罩热环境参数Tab.1 Thermal environment parameters of the fuse radome

烧蚀过程天线罩受到高热流密度的作用，其端头外形会发生激烈变化，由于天线罩表面粗糙度分布具有随机分布的特性，烧蚀外形亦具有随机分布的特性，即小不对称外形[7]。本文在统计烧蚀量时以天线罩驻点位置的后退距离作为结果进行统计，图3为各时刻下引信天线罩的烧蚀量。整个过程中，引信天线罩受烧蚀总时间为120 s，总烧蚀量为26 mm。

图3 天线罩驻点烧蚀量Fig.3 Ablation at the stagnation point of the radome

图4给出了聚四氟乙烯材料引信天线罩驻点位置随时间变化的烧蚀速率曲线。初始阶段，天线罩表面受到热流冲击时，流场的热流量较小，温度升高缓慢，因此在15 s之前的烧蚀量较少，烧蚀速率也比较缓慢；在20 s时刻时随着表面的热流增大，表面温度也迅速上升，此时的化学反应速率加快，导致材料烧蚀率迅速增加；29～36 s这段时间内随着烧蚀表面热流随着时间达到动态平衡，烧蚀率趋于平稳，在30 s时烧蚀率达到最大为1.21 mm/s；36～40 s之间天线罩受到的热流大幅度减少，因此烧蚀率也迅速下降；40～120 s时间段天线罩表面温度变化基本处于稳定状态，此时烧蚀率主要受表面热流变化影响，烧蚀速率随着表面热流减小而下降。整个过程天线罩材料受到烧蚀后退量为26 mm。

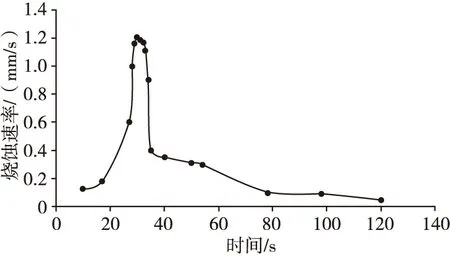
图4 天线罩驻点烧蚀速率Fig.4 Ablation rate of the radome stagnation point

3.2 试验验证

根据气动热理论计算分析，确定气动热环境，模拟该气动热环境进行地面电弧热风洞试验。实验室可以模拟的条件为驻点压力、驻点温度和驻点热密度，根据实验室的试验条件，选取特定的时刻下引信天线罩气动热环境，获得各个时刻下热环境数值。设备为25 MW电弧加热器，试验出口截面尺寸为Φ90 mm，主要调参数恢复焓h和压力p，用于进行驻点天线罩试验。

试验台阶设计如表2所列，根据理论计算，对试验设备进行状态调试，保证测试点的热流与理论计算相同。经过试验调试，从引信天线罩端头170 mm长度内的气动热环境与理论值基本相符，可以有效降低测试误差。引信天线罩表面的温度使用红外热像仪获取以避免因采用接触方法带来的对试验体的破坏，采用热电藕传感器测量，该电阻具有较高的精度。

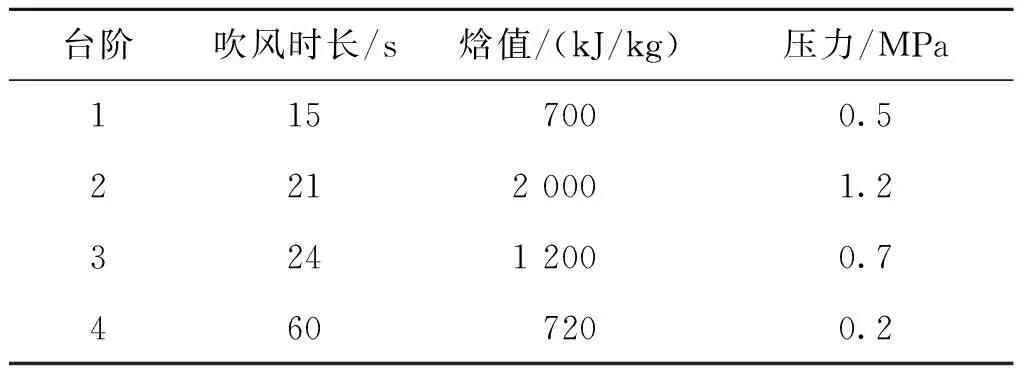
表2 试验台阶设计Tab.2 Step design for the test

图5为引信天线罩电弧热风洞试验后结果。从图中可以看出引信天线罩前端出现了小不对称的烧蚀形状，烧蚀的黑色痕迹说明其过程中产生了碳的氧化反应，经测量天线罩沿轴向烧蚀退后最大距离为24.3 mm，试验结果测量结果与计算结果对比值见表3。

图5 天线罩热风洞试验结果Fig.5 The experimental result of arc hot wind tunnel in the fuze radome

通过表3可以看出，试验结果与计算结果基本一致，引信天线罩各个时段的烧蚀速率变化规律基本相同。其中烧蚀量计算结果与试验结果最大误差为9%，烧蚀速率计算结果与试验结果最大误差为29%。由此可以说明，本文采用简化的聚四氟乙烯材料烧蚀算法能够较为准确地计算出引信天线罩的烧蚀情况。

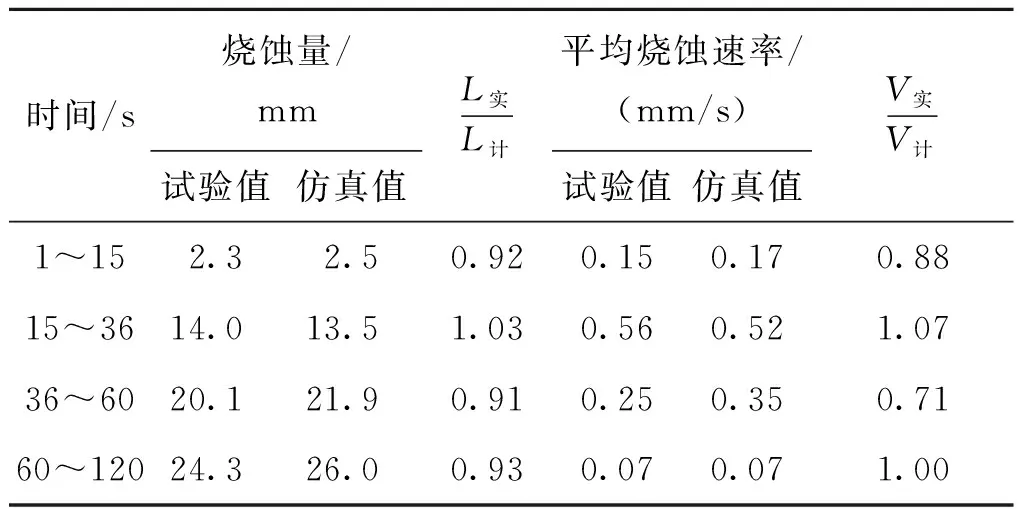
表3 数值模拟与试验结果的比较Tab.3 Comparison between the numerical simulation and experimental results

4 结论

本文提出了聚四氟乙烯材质引信天线罩烧蚀算法。该算法基于碳基复合材料的烧蚀理论，对聚四氟乙烯材料烧蚀算法进行了简化。给出了聚四氟乙烯的表面烧蚀化学方程，确定了组元浓度，建立了烧蚀模型，通过计算质量损失求得材料的烧蚀率。仿真试验结果表明，烧蚀量计算最大误差为9%，烧蚀速率计算最大误差为29%。造成这种误差的原因一方面是本文在建立烧蚀模型时对反应方程进行了简化，选取氟化物反应为烧蚀主要方程，实际烧蚀过程中氮元素也参与了反应，而氮元素的反应产物会对氟化物的反应速率产生影响，进而会影响烧蚀速率；另一方面是本文在计算时没有考虑烧蚀作用导致引信天线罩气动外形改变所带来的影响。在实际的烧蚀过程中，由于天线罩烧蚀后的形状反作用于气流，使外弹道原本的流场发生了变化，进而造成天线罩所受到的气动热条件发生了变化，最终导致烧蚀速率会发生变化。这两方面因素对烧蚀计算的影响还需进一步研究。总体上本文采用的烧蚀算法是可行的，能够准确地计算出引信天线罩受气动热烧蚀的情况。