稀疏表示系数下局部最优重构的SAR图像目标识别算法
唐吉深,覃少华
(1.河池学院,广西 河池 546300;2.广西多源信息挖掘与安全重点实验室,广西 桂林 541004;3.广西师范大学计算机科学与信息工程学院,广西 桂林 541004)
0 引言
自20世纪90年代以来,合成孔径雷达(synthetic aperture radar, SAR)图像目标识别问题在世界范围内得到广泛研究并产出了大量的成果[1-2]。SAR目标识别系统通过检测、鉴别和分类的三个阶段从大场景图像中获取感兴趣的目标并判定其类别。现有公开的SAR目标识别算法主要集中在对分类算法的研究,即在已经剔除虚警后的感兴趣目标区域(region of interest,ROI)的基础上对其类别进行决策(后文将其称为SAR目标识别)。一般的SAR目标识别算法主要设计特征提取和分类决策两个环节。前者通过分析目标几何形状、灰度分布以及电磁散射等特点获取低维特征矢量,实现对目标核心特性的有效描述。文献[3—5]以目标区域、轮廓等为基本特征设计SAR目标识别算法。文献[6—9]采用主成分分析(principal component analysis,PCA)、非负矩阵分解(non-negative matrix factorization,NMF)、单演信号分解等手段获取SAR图像的不变特征。文献[10—11]基于属性散射中心设计SAR目标识别方法,通过散射中心的一一配对考察目标可能出现的局部变化。分类决策阶段,根据提取特征的不同规律和特点,选用相适应的分类机制。目前,在SAR目标识别中广泛运用的分类器包括K近邻(K-NN)[6]、支持向量机(support vector machine,SVM)[12]、稀疏表示分类(sparse representation-based classification,SRC)[13]以及深度网络[14-15]等。
稀疏表示目前已在模式识别领域获得到广泛运用。Wright等人[16]首次将稀疏表示运用于人脸识别并根据各训练类别的重构误差进行决策;Thiagaraianm等人[13]将稀疏表示分类引入SAR目标识别;后续,稀疏表示分类成为SAR目标识别中广泛运用的分类器之一,对于多种特征均有良好的适应性。这些算法多是基于最小重构误差准则进行分类决策。文献[17]提出基于最大系数能量的决策方法,其基本思想是计算各个类别上系数的能量和,根据最大能量的准则进行决策。无论是最小重构误差准则还是最大系数能量准则,它们的应用并没有深入分析SAR目标识别这一问题的特殊性。与光学图像不同的是,SAR目标图像对于方位角变化具有很强的敏感性[18]。因此,在稀疏表示过程中,只有与测试样本具有相近方位角训练样本才是有效的,其余样本的引入容易造成更大的误差。文献[19]正是利用SAR图像的方位角敏感性设计了方位角区间内的稀疏表示方法(SRCA)并应用于目标识别。本文针对当前相关研究存在的问题提出全局稀疏表示系数下局部最优重构的SAR目标识别方法。
1 稀疏表示分类
稀疏表示的基本思想是采用预先构建的字典对特性位置的样本进行稀疏重构,从而根据表示稀疏的分布规律对未知样本的特性进行有效评估。具体在目标分类邻域,字典一般由类别确定的训练样本构建然后对待分类的测试样本进行表示。假设D=[D1,D2,…,DC]∈Rd×N为来自C个类别的全局字典,其中Di为来自第i类别的Ni个训练样本,对测试样本y的稀疏表示过程可描述如下:
(1)
式(1)中,x为待求解的稀疏表示系数矢量,ε为重构误差的约束门限。式(1)中的优化问题难以直接求解。为此,研究人员通过1范数等效[16]或贪婪算法(如正交匹配追踪算法(orthogonal matching pursuit,OMP))[13]获得近似解。
在获得稀疏表示系数的基础上,按照式(2)计算各个类别对于测试样本的重构误差。
(2)
式(2)中,xi为对应于第i类的系数;r(i)为相应的重构误差。
传统的稀疏表示分类大多根据重构误差的大小进行类别判定,即具有最小重构误差的训练类别为测试样本的目标类别。后续,也有研究人员根据各类别系数能量的大小作为判决依据。需要指出的是,这些方法都在所有非零表示系数上进行决策,缺乏对独立原子的考察。实际上,由于SAR图像自身具有的特性,对稀疏表示系数进行更深层次考察和分析有利于获得更为准确的分类结果。
2 局部最优重构的目标识别算法
2.1 SAR图像方位角敏感性
SAR图像具有较强的方位角敏感性,即当目标和雷达平台的方位向视角变化较大时,图像中的目标特性表现出很大的差异。这一特性导致了同一目标的不同方位角SAR图像之间的差异往往超过了不同类别之间的某些图像差异,给识别问题带来较大的混淆。同时,在多视角样本可利用的条件下,方位角敏感性又为多视角识别方法提供了更充分的信息。不同视角之间相互补充从而为目标类别的确认提供了更强的鉴别力,文献[20—22]正是基于此设计了多种多视角SAR目标识别方法。
传统基于稀疏表示的SAR目标识别方法的决策思路与光学图像识别一致,并没有考虑到SAR图像的方位角敏感性。实际上,对于SAR图像测试样本,与其高度相关的原子(无论是来自正确类别还是错误类别)应当与其具有相近的方位角。因此,针对SAR目标识别的稀疏表示系数应该具有明显的方位角区间特性。这一特性的引入有利于进一步增强稀疏表示系数以及重构误差区分不同类别的能力,从而提高目标识别性能。
2.2 基于局部最优重构目标识别方法
本文在全局稀疏表示的基础上提出局部最优重构方法。本方法通过SAR图像方位角敏感性的引入进一步考察各训练类别对于测试样本的真实表征能力。对于全局字典,按照方位角升序的方式对其中各个类别的训练样本分别进行排列。对于求解的稀疏表示系数矢量,选取其中P个最大的系数,记为x(P)。这一步的目的主要是剔除大量无关原子(即与测试样本的方位角差异很大)的影响。根据选取的原子及其对应的系数,分别在各个类别上对测试样本进行重构:
(3)

saz(i)=var([k1,k2,…,kMi])
(4)
式(4)中,函数var()计算方差。当选取原子之间聚集性较差时,方差相对较大;反之,方差相对较小。据此对式(3)中的重构误差进行加权修正,得到最终的决策变量如下:
dv(i)=exp(saz(i))·rL(i)
(5)
式(5)计算得到的决策变量与重构误差具有一致的含义。通过方位角聚集系数的引入使得最终的决策变量更具可靠性。分类阶段,根据式(5)计算的各类别对应的决策变量,采用最小误差原则进行目标识别。因此,相比于传统的全局稀疏表示,本文方法的目标是在局部字典上通过利用方位角的敏感性获得最优重构,并通过分析稀疏系数的分布规律进一步突出真实类别与虚假类别之间的差异,从而提升最终的识别性能。
本文主要是在传统稀疏表示的基础上针对SAR目标图像的特性进行改进,设计了更适用于SAR目标识别的新方法。图1为提出方法的基本流程。对于测试样本,首先在全局字典上对其进行稀疏表示,获取系数矢量;根据当前识别问题的规模(待识别的类别数量)选取少量的最大系数并在各个类别上对测试样本进行重构;最后,按照式(4)计算各类别上系数的方位角聚集系数并对重构误差进行修正,获取最终的决策矢量进行目标识别。方法的具体实施中,从全局稀疏表示系数中选取P=5C个最大系数;采用经典的PCA对测试和训练样本进行特征提取,从而降低计算复杂度。

图1 方位角敏感性约束下局部最优重构的SAR目标识别方法流程Fig.1 Procedure of SAR target recognition based on local optimal reconstruction under the constraint of azimuthal sensitivity
3 实验与分析
3.1 MSTAR数据集
为验证提出方法的有效性,基于MSTAR数据集开展实验。该数据集中包含如图2所示的10类车辆目标,各类目标图像由X波段SAR传感器采集,成像模式为聚束模式,分辨率0.3 m。对于任一类目标,其SAR图像样本的相邻方位角间隔约为1°~2°。现阶段,大多数公开文献中的SAR目标识别算法均是基于MSTAR数据集进行性能测试,表明其权威性。
标准操作条件(standard operating condition)和扩展操作条件(extended operating condition)是SAR目标识别中两类情形。标准操作条件指的是当前测试样本与构建的训练(模板)样本差距较小,可近似认为采集自相同的条件。反之,扩展操作条件则是指由于测量条件(包括背景环境、目标自身、传感器等因素)的变化,测试样本与训练样本存在较大的差异。典型的扩展操作条件包括型号变化、俯仰角变换、噪声干扰等。为了充分验证提出方法的性能,本文在后续实验中分别在标准操作条件和部分扩展操作条件下对其进行测试。同时,选用若干对比方法进行同步测试,分别为文献[13]中基于最小重构误差分类原则的SRC方法(记为“最小误差-SRC”),文献[17]中基于最大系数能量的SRC方法(基于 “最大能量-SRC”),文献[19]中基于SRCA的方法,文献[12]基于SVM的方法以及文献[14]中基于全卷积神经网络(A-ConvNets)的方法。其中,前两个对比方法与本文方法一样,采用SRC作为基础分类器,但其具体的决策准则与本文不同。

图2 10类目标的光学图像Fig.2 Optical images of the ten targets
3.2 标准操作条件
标准操作条件下的识别问题相对简单,但它是对SAR目标识别算法的基本考核。表1给出了当前基于MSTAR数据集设置的一种典型标准操作条件,包含了其中全部10类目标。其中,训练和测试样本来自相同的目标型号,唯一的区别为2°的俯仰角差异(两者分别来自17°和15°俯仰角)。图3显示了提出方法在标准操作条件下的分类结果,各类目标的正确识别率如对角线所列,综合得到10类目标的平均识别率为98.74%。
表2对比了各类方法在标准操作条件下的识别性能。在识别精度方面,本文方法的平均识别率略低于A-ConvNets方法而优于其他方法。在标准操作条件下,训练样本与测试样本相似高,能够较好覆盖测试样本中出现中的各种情形。因此,训练得到的卷积神经网络分类能力很强,能够取得很高的识别率。与其他三类基于SRC的方法相比,本文方法的识别率有一定的提高,表明通过局部最优重构能够有效改善识别性能。方位角约束下的SRCA方法相比最小误差-SRC和最大能量-SRC具有更高的识别率,表明充分利用SAR图像的方位角敏感性有利于提升整体识别性能。在相同的硬件平台上对各类方法进行测试并计算它们识别单个测试样本所需的时间消耗。从表中可以看出,本文方法的效率低于最小误差-SRC和最大能量-SRC方法但高于其他方法。由于本文方法在决策变量的计算中充分考虑了稀疏系数矢量的局部特性因此相比简单最小重构误差和最大系数能量需要更多的时间消耗。对于SVM和A-ConvNets方法,它们则需要分类器的训练时间。综合来看,本文方法在标准操作条件下的性能较优,能够较好地完成多类目标的识别任务。

表1 标准操作条件的典型实验设置Tab.1 Typical experimental setup under SOC

图3 本文方法在标准操作条件下的分类结果Fig.3 Classification results of the proposed method under SOC

表2 各方法标准操作条件下的性能比较Tab.2 Performance comparison of different methods under SOC
3.3 扩展操作条件
3.3.1 型号变化
目标自身型号变化时SAR目标识别中一种典型扩展操作条件,主要是指测试样本的目标型号与训练样本存在差异。表3给出了基于MSTAR数据集设置的型号变化条件下的训练和测试集。其中,BMP2和T72的测试型号与训练样本完全不同;BTR70的引入主要是为了进一步增加识别问题的难度。表4对比了各类方法在型号变化条件下的平均识别率,本文方法性能最优。当训练样本与测试样本存在一定差异时,训练得到的卷积神经网络分类性能出现下降,这也是当前基于深度学习方法的方法对于大量训练样本的依赖性。与其余两类SRC方法相比,本文方法在型号变化条件下仍然能进一步提高识别稳定性,表明了设计的局部最优重构算法的有效性。

表3 型号变化下的典型实验设置Tab.3 Typical experimental setup under configruation differences
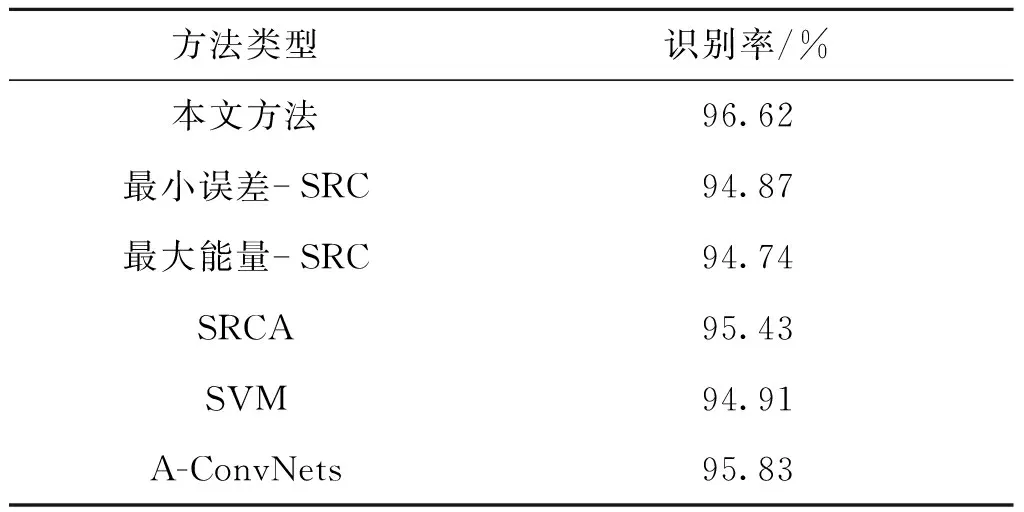
表4 各方法型号变化下的平均识别率Tab.4 Average recogntion rates of differnet methods under configuration differences
3.3.2 俯仰角变化
随着训练和测试样本俯仰角差距的不断增大,识别问题也不再是标准操作条件。由于较大俯仰角差异带来的SAR图像差异使得识别问题尤为困难。基于MSTAR数据集设置如表5所示的训练和测试集,3类目标以17°俯仰角下的图像作为训练集分别对30°和45°俯仰角下的测试样本进行分类。各类方法在不同俯仰角的平均识别率如图4所示。显然,由于俯仰角差异相对较小,30°下的识别性能远远优于45°下的性能,主要是因为28°的大幅俯仰角变化使得测试样本和训练样本出现了很大的差异。对比各类方法,本文方法在两个角度下都取得了最佳的性能,验证其对于俯仰角差异的稳健性。在俯仰角变化较大的情况下,可用于表征测试样本的训练样本不断减少。因此,通过选取合适的训练样本进行最优重构有利于避免无效样本的影响从而提高决策的可靠性。
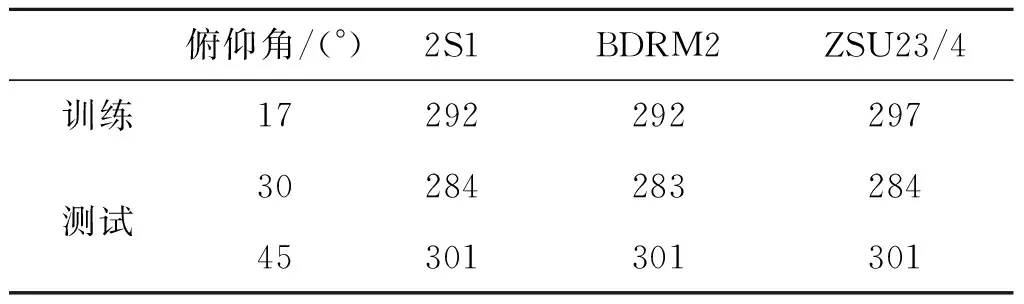
表5 俯仰角变化下的典型实验设置Tab.5 Typical experimental setup under depression angle differences

图4 各方法在不同俯仰角下的平均识别率Fig.4 Average recognition rates of different methods at different depression angles
3.3.3 噪声干扰
噪声伴随着SAR数据采集以及成像的整个过程。尽管现阶段已经有了一些SAR图像噪声抑制算法,但噪声仍然是影响SAR目标识别性能的重要因素。原始MSTAR数据集信噪比(signal-to-noise ratio,SNR)较高,难以直接考察目标识别算法在低噪声水平下的性能。为此,本文首先按照文献[10]中的策略向表1中的训练样本添加噪声,然后基于构造的噪声样本测试各方法在噪声干扰条件下的分类性能。图5为各类方法在不同信噪比下的识别率曲线。显然, 噪声水平的不断提高导致各类方法的识别性能均出现了明显的下降。对比可见,本文方法对于噪声干扰具有更强的稳健性。此外,基于SRC的四类方法对于噪声干扰表现出更好的适应性,尤其在低信噪比的条件下,性能优势更强,这与文献[16]中的实验结果具有一致性。对于A-ConvNets方法,受噪声干扰影响,基于高信噪比(原始)训练样本训练的网络对于低信噪比的SAR图像的适应性较差。
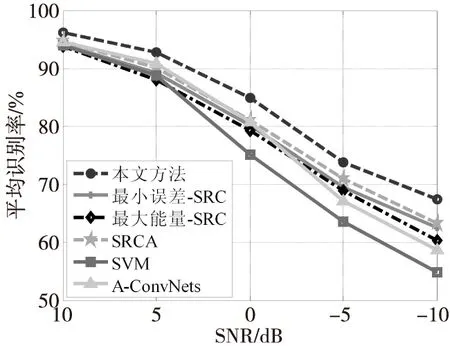
图5 各方法在噪声干扰下的平均识别率Fig.5 Average recognition rates of different methods under noise corruption
3.4 方位角间隔大小影响
在局部重构中,按照升序排列的相邻原子方位角间隔对算法性能存在影响。采用原始MSTAR数据集时,相邻原子方位角间隔约为1°~2°,此时两幅SAR图像具有较高的相似性。随着这一间隔的增大,相邻图像的相关性降低,会一定程度破坏稀疏系数的局部聚集性规律。为此,本实验在原始局部字典的基础上通过去除部分原子的思路,考察方位角间隔的影响。具体的,在基于表1设置的实验条件下,对局部字典中的原子进行抽样,并统计识别结果如表6所示。其中,“隔1取1”表示在原始局部字典中间隔1个保留下1个,去除中间的原则,其余条件同理。从结果可以看出,随着方位角间隔的不断增大,各类方法的性能均出现下降。对于几类对比方法,它们性能下降主要是由于可用训练样本的规模减小,导致分类器的可靠性下降。本文方法除了上述原因外,还存在大方位角间隔条件下局部原子结构的破坏,导致性能下降。总体来看,本文方法在“隔1取1”和“隔3取1”两种条件下还可以保持最高识别率,但在“隔5取1”条件下性能不再是最优。这样反映了方位角间隔增大对所提方法的影响。

表6 各方法在方位角间隔变化条件下的平均识别率Tab.6 Average recogntion rates of differnet methods under variation of azimuthal interval
4 结论
本文提出稀疏表示下局部最优重构的SAR目标识别算法。该算法通过在全局字典上求解得到的稀疏表示系数选取若干最大的系数;然后,根据选取的系数分别在各个训练类别上对于测试样本进行重构;同时,根据SAR图像的方位角敏感性对各类别上的系数结构进行分析,并与各类别的重构误差进行结合,获得最终的决策变量完成目标识别。实验结果表明,该方法在标准操作条件和扩展操作条件下均可以取得更好的性能。

