基于L2范数的高斯混合模型空域去噪方法

王彩玲，孙昌霞

(1.河南警察学院网络安全系，河南 郑州 450046;2.河南农业大学信管学院计算机系，河南 郑州 450046)

0 引言

由于图像在获取、传输和数字化过程中会遇到不同光照的影响，传感器温度发生变化等情况，获取的图像中会引入随机噪声。图像去噪的方法很多，常分为频域滤波和空间域滤波。常用的频域滤波方法有小波去噪[1]、高通滤波、维纳滤波[2]等；空域滤波的方法很多，如偏微分方程、变分法[3]、统计方法[4]等，这些方法均有较多的应用。经典的偏微分方程法是一种各向同性的滤波算法，能很好地去除噪声，但这类方法在对噪声成分进行平均的同时也对图像信息进行了平均，导致处理后的图像变得较为模糊。Yaroslavsky根据像素灰度的差异来定义像素点之间的相似性，得到了Yaroslavsky滤波[5]。Tomasi在Yaroslavsky滤波的基础上，结合像素点间的灰度差异和空间距离来定义了像素间的相似性，得到了双边滤波[6]。近年来，对双边滤波也出现了一些改进算法[7-11]，主要集中于滤波参数的选择、算法效率的提升等方面，其中，文献[12]提出了距离核的概念，将其应用于像素相似性权值的定义中，在细节丰富的区域中，算法的去噪性能有很大的提升。此外，文献[13]提出了一种基于方向波域混合高斯模型的合成孔径雷达图像去噪方法。与小波域不同，文献[14]对合成孔径雷达图像进行复Shearlet变换，并对系数进行高斯混合模型建模，有效提升去噪图像的峰值信噪比。

针对图像像素间相似性衡量不准确而导致去噪性能下降的问题，本文利用高斯混合模型对像素周围邻域内的像素信息进行建模，结合高斯混合模型间的L2范数与空间距离来定义像素点之间的相似性权值，提出基于L2范数的高斯混合模型空域去噪方法。

1 基于高斯混合模型的图像去噪原理

基于高斯混合模型的图像去噪的基本思想：首先利用每一个像素点周围邻域的像素信息估计出高斯混合模型的参数，将像素信息建模为高斯混合模型，得到预滤波图像；然后计算两像素点对应高斯混合模型间的L2范数，结合L2范数值和两像素点间的空间位置距离来定义两像素点间的相似性权值；最后对每一个像素点进行加权平滑滤波，得到去噪后的图像。

与经典的空域去噪方法不同，基于高斯混合模型的图像去噪方法是根据像素点周围信息的统计差异性大小来定义像素点间的相似性权值，其具体步骤如下：

1) 对某一个像素点，利用其周围邻域内的像素信息估计出高斯混合模型的参数，得到一个高斯混合模型；

2) 对图像中的每一个像素均估计出一个高斯混合模型，所有的高斯混合模型构成了一个预滤波图像；

3) 计算两像素点对应高斯混合模型间的L2范数，并结合两像素点间的空间距离来定义像素点间的相似性；

4) 对图像中的每一个像素均进行加权平滑滤波，得到滤波后的图像。

从上述步骤可知，基于高斯混合模型的图像去噪是根据两像素点x与y间的空间距离和其对应高斯混合模型间的L2范数来定义相似性权值w(x,y)，并进行加权平滑滤波得到滤波后的图像，滤波公式如下：

(1)

(2)

式(2)中，G(x)和G(y)分别表示像素点x与y处的高斯混合模型，d2(x,y)=|x-y|2表示像素点x与y间的空间距离，参数r是滤波控制系数。r越大，图像的平滑效果越好，图像的细节信息损失越多；r越小，图像的平滑效果越差，图像细节信息损失越小。因此，在滤波过程中需要选择合适的滤波控制系数r。基于高斯混合模型的图像去噪方法的基本思想可表示如图1所示。

图1 基于高斯混合模型的图像去噪Fig.1 Image denoisingbased on Gaussian mixture model

2 基于L2范数的高斯混合模型去噪

对每一个像素点，利用其周围邻域内的像素信息估计出高斯混合模型的参数，得到一高斯混合模型。像素点对应的高斯混合模型表示该像素周围邻域内像素信息的局部灰度强度和细节丰富程度，利用两高斯混合模型间的L2范数，并结合像素点间的空间距离来定义像素间的相似性权值。依据该相似性权值对图像中的每一个像素进行加权平滑滤波，下面主要介绍像素信息的高斯混合模型建模以及两高斯混合模型间的L2范数计算。

2.1 像素信息的高斯混合模型估计

对某一像素点x，其周围邻域窗口Ψ(x)的大小为M×M，邻域内包含M2个像素点，位置(i,j)处的像素灰度值为I(i,j)，利用这些像素信息估计出一高斯混合模型，公式如下：

(3)

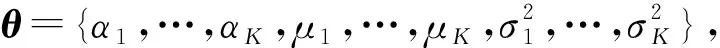
(4)

式(4)中，z表示类别的标签，P(·)表示概率大小。式(4)给出γim,i=1,…,n2,m=1,…,K的计算公式，进一步，依据式(4)可计算出其余的参数：

(5)

根据式(4)和式(5)可以利用EM算法迭代估计出高斯混合模型的参数，参数估计的具体步骤如下：

1) 对参数θ取初值；

4) 重复步骤2)和步骤3)，直至收敛。

采用上述步骤可以估计出每个像素点的高斯混合模型的参数，所有像素点对应的高斯混合模型即构成了预滤波图像，在预滤波图像中，结合两像素点对应高斯混合模型间的L2范数和空间距离来计算两像素点之间的相似性权值。为了分析利用EM算法进行高斯混合模型参数估计的有效性，以某次参数估计为例，对于给定7×7的图像区域的像素信息，利用此49个像素进行高斯混合模型的参数估计，选取模型的成份数为5，其参数估计的中间结果如表1所示。

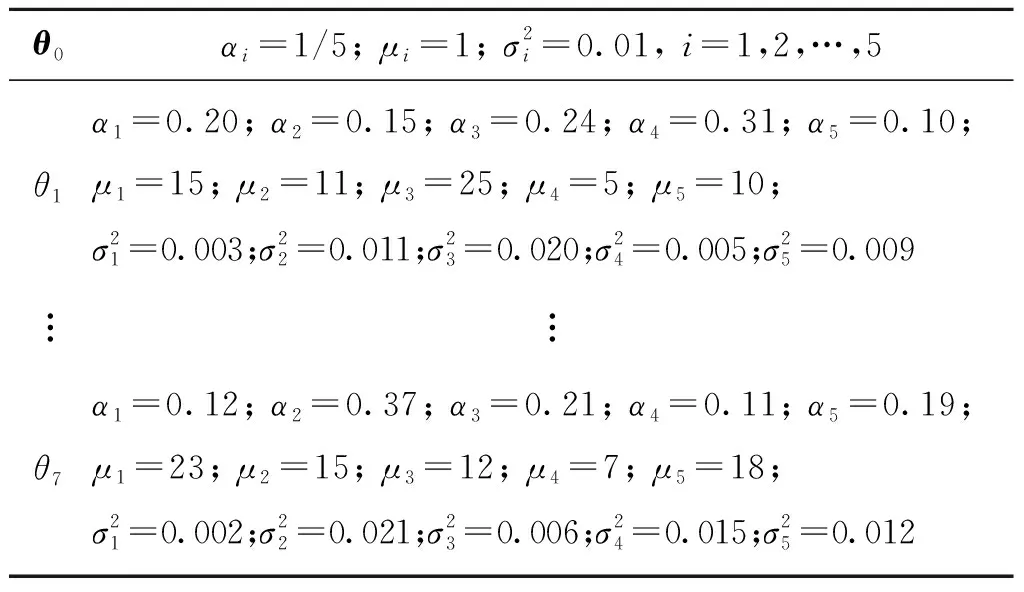
表1 高斯混合模型的参数估计的中间结果Tab.1 Intermediate results of parameter estimation

从表1的结果可以看出，利用EM算法进行高斯混合模型的参数估计，在第7步时算法收敛，并且不同高斯成分对应的权值以及均值和方差均不相同。

2.2 L2范数的计算

假设每个像素点周围的像素信息建模为混合成份数均为K的高斯混合模型，对于两像素点x与y对应的高斯混合模型为：

(6)

其间的差异性度量计算方法较多，如KL散度、蒙特卡洛方法等，但KL散度并没有解析表达式，只能通过近似的方式来计算，蒙特卡洛方法的计算量太大，均不适合。为此，本文采用L2范数来计算两高斯混合模型间的差异性，高斯混合模型间的L2范数具有解析表达式，便于算法的实施。

对于高斯混合模型G(x)与G(y)，其间的L2范数可计算如下：

(7)

上式展开可得，

(8)

将式(6)代入式(8)，化简可得，

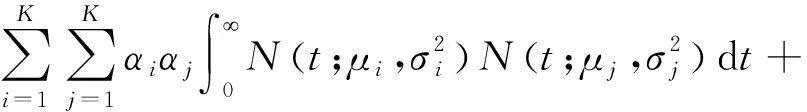
(9)

根据高斯分布的积分性质可知，

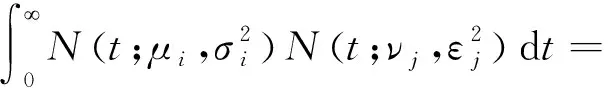
(10)

将式(10)代入式(9)，化简可得，

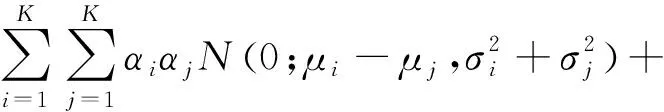
(11)

根据式(11)，可计算两高斯混合模型间的L2范数距离。

The acoustic impedance of the perforated plate is related to the acoustic resistance and mass reactance of the orifice on the assumption that the interaction between the orifices,if they are sparsely distributed,can be neglected.

3 实验验证

3.1 评价指标

对去噪算法的评价须从两个指标进行评价，即去除噪声的多少和图像细节信息损失多少。噪声去除的越多，表明去噪算法的去噪能力越强；噪声去除的越少，表明算法的去噪能力越差。同时，图像细节信息保留越多，表明图像的质量越好；图像的细节信息保留越少，表明图像的质量越差。通常在去除图像噪声的同时，尽可能多地保留图像的细节信息。为此，本文采用峰值信噪比(peak signal to noise ratio，PSNR)来衡量算法的去噪能力，同时，采用结构相似度因子(structural similarity index，SSIM)[15]来评价去噪后图像的质量好坏，也即图像的细节信息保留的能力。PSNR的值越大，SSIM的值越接近1，说明算法的去噪能力越强，且图像的细节信息保留越多。

3.1.1PSNR

在图像去噪的算法评价中，PSNR常用于图像去噪能力的评价指标，PSNR可计算如下：

(12)

式(12)中，vmax表示图像中的最大像素值，在0～255的图像中，vmax=255；v(i)和u(i)分别表示噪声图像和无噪声图像的灰度值，mean{[v(i)-u(i)]2}是指噪声的平均功率。

3.1.2SSIM

结构相似度因子是根据人类视觉机制来定义的图像去噪的评价指标，从视觉上来看图像，图像的细节信息越多，则图像越清晰，反之，图像越模糊。SSIM是结合图像的对比度、边缘结构和图像亮度等三方面的特性，通过加权乘积得到的评价指标，SSIM可由如下公式计算：

(13)

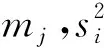
在本文中，c1=(k1L)2，c2=(k2L)2，L表示像素值的取值范围，k1和k2是权系数，一般情况下，k1=0.01，k2=0.03。一幅图像的SSIM是不同窗口内SSIM的均值mSSIM。

3.2 实验结果分析

为了验证本文算法(GMMD)的有效性，首先需要分析算法的处理过程，包括相似性权值的分析，待滤波图像的求解，然后分析去噪效果。算法在联想笔记本上运行，其环境为Windows 10系统，处理软件为matlab 2019a，CPU采用英特尔i7-8850H，内存16 G。

对于一幅“Lena”图，从中选择A、B、C、D 4个区域，依据相似性权值的计算公式分别计算A与B、C、D之间的相似性。结果如图2所示：A与B之间的像素信息差异较大，其相似性较低，只有0.31；A与C之间的像素信息比较接近，其相似性高达0.92；A与D之间的颜色信息有一定的差异，其相似性适中，有0.75。上述相似性的结果能较好地反映出不同区域间的差异性大小，为加权平均滤波奠定了基础。

图2 图像不同区域的相似性Fig.2 Similarity of different regions in image

为了进一步分析算法的有效性，需要给出图像的预滤波图像。如图3所示，分别给出了原图像、噪声方差为0.01的图像、均值图像以及方差图像，其中均值和方差图像为预滤波图像，说明了图像在均值和方差域的信息。

从图3的结果可以看出，均值图能较好地反映出图像的像素信息，而方差图能反映出图像的边缘细节信息，利用高斯混合模型能较好地建模图像区域像素信息的局部灰度强度和细节丰富程度。

从图4—图8的去噪结果可以看出，GMMD算法和KBF算法的去噪性能明显优于MF和BF的性能，GMMD算法能很好地去噪图像噪声，同时能较大程度上保留图像的细节信息。为了从视觉上更好地看出不同方法的去噪性能，在图像中选取某一区域，给出其去噪结果，以“Lena”图为例，选取的图像区域以及去噪结果如图9所示。

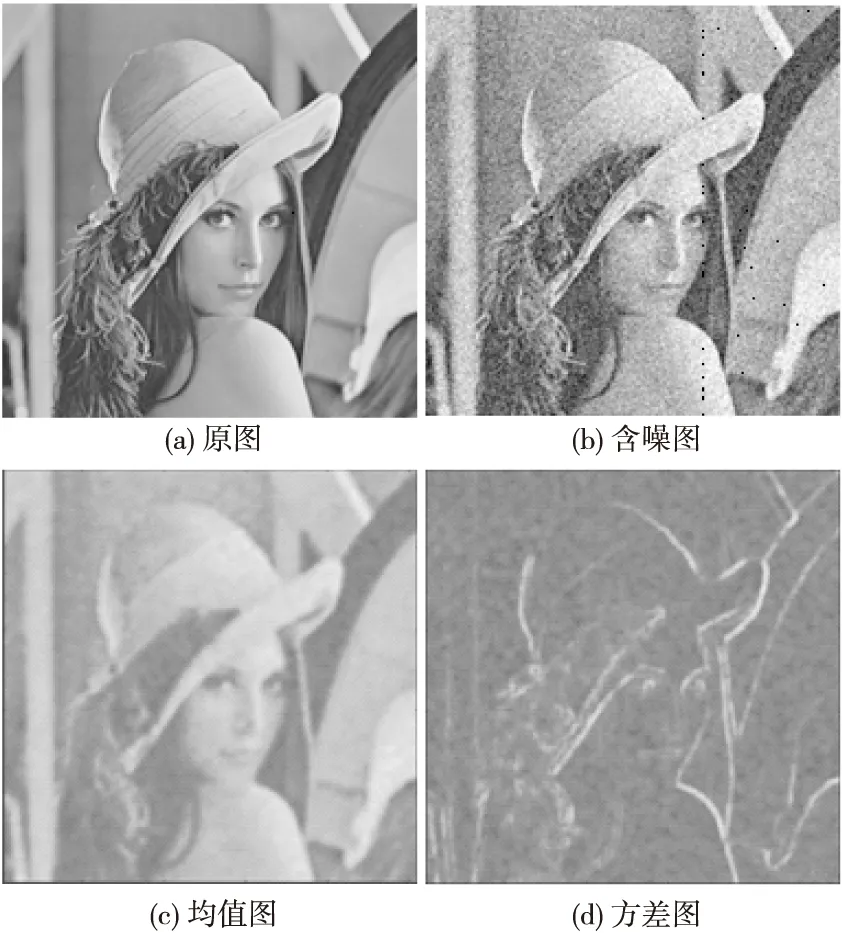
图3 图像的预滤波结果Fig.3 Pre-filtering results

图4 噪声图像Fig.4 Noise images

图5 经BF去噪后的图像Fig.5 Denoised images by BF

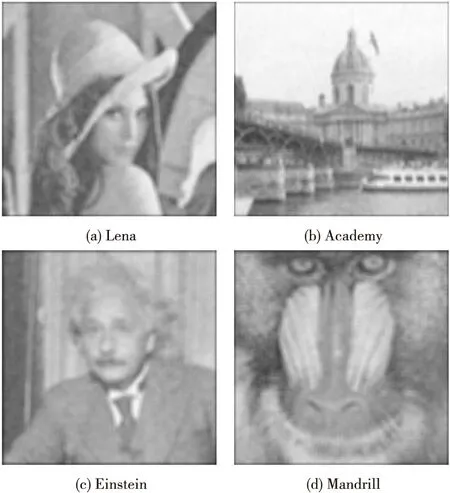
图6 经MF去噪后的图像Fig.6 Denoised images by MF

从图9的结果可看出：图像区域经MF去噪后细节信息损失较多，图像较模糊；利用BF和KBF进行去噪后，得到的结果虽然细节保持较好，但噪声较多，去噪效果较差；而本文方法得到的去噪结果不仅在图像细节信息上保持较好，而且能去除噪声，去噪效果较好。为了定量分析和比较GMMD算法的性能优势，在不同噪声背景下，利用不同去噪算法进行去噪实验，计算PSNR和mSSIM的值，所得结果如表2和表3所示。

图7 经KBF去噪后的图像Fig.7 Denoised images by KBF

图8 经GMMD去噪后的图像Fig.8 Denoised images by GMMDX

从表2和表3的结果可得，GMMD算法和KBF算法的去噪能力和细节信息保留能力均优于MF和BF算法。在比较平坦的图像“Lena”和“Einstein”去噪结果中，GMMD的去噪能力和细节信息保持能力均优于KBF算法；然而，在图像细节信息较丰富的图像“Academy”和“Mandrill”去噪结果中，GMMD算法的去噪性能提升并没有像平坦区域那么大。结合图像像素信息的局部平均灰度强度和细节丰富程度来定义像素间的相似性权值，比传统的方法更准确。

图9 局部区域的去噪结果Fig.9 Denoising results of local area

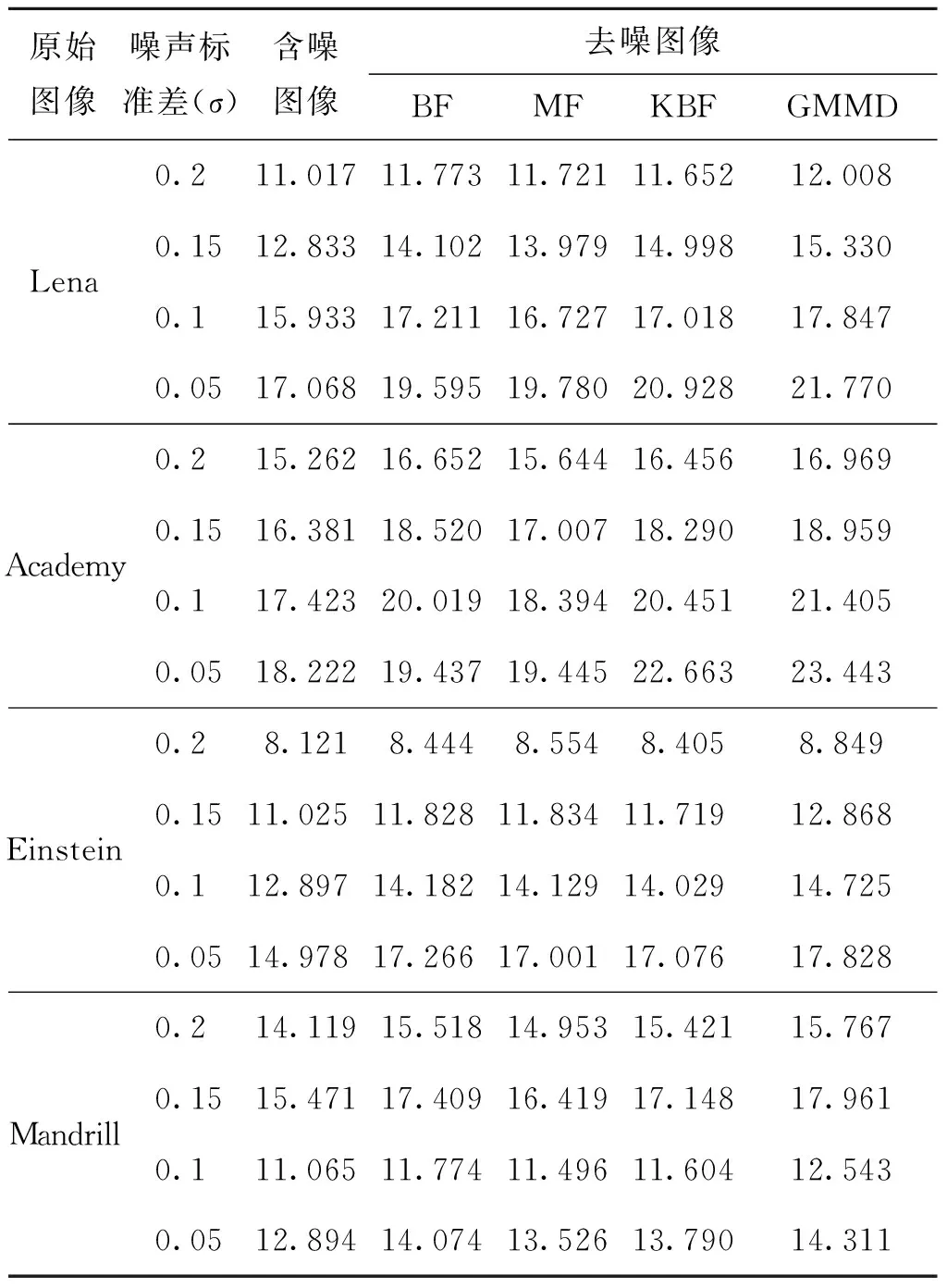
表2 不同去噪算法的PSNRTab.2 PSNR of different denoising algorithms dB

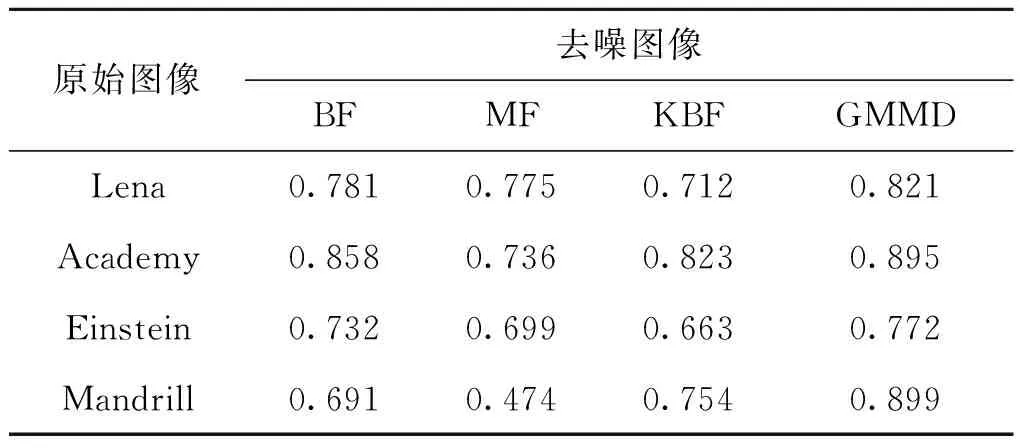
表3 不同算法的mSSIM(σ2=0.01)Tab.3 mSSIM of different denoising algorithms

4 结论

本文提出了基于L2范数的高斯混合模型空域去噪方法。该方法将像素点周围像素的局部灰度信息的统计特性建模为高斯混合模型，结合高斯混合模型间的L2范数和像素位置的空间距离来定义像素点之间的相似性权值，以提高像素间相似性度量的精确度，利用加权平滑滤波来对图像进行去噪处理。实验结果表明，利用高斯混合模型可更加准确地衡量像素间的相似性，同时，该去噪方法可提高图像的去噪效果，并能较好地保留图像的细节信息。如何在细节丰富的图像区域中提升算法的去噪性能，是下一步研究的重点。