基于离散余弦变换的单像素相机测量矩阵的性能评估

程 涛，吴小龙，杨 明

(广西科技大学机械与交通工程学院,广西 柳州 545006)

0 引言

根据压缩感知(compressed sensing, CS)理论可知，如果信号是稀疏的就能以远低于奈奎斯特(Nyquist)采样频率的采样率采集信号，并能高概率精确恢复信号[1-4]。但是，电、光、声、磁、热和机械等一维、二维或多维信号多非稀疏，可压缩。可压缩信号需做稀疏变换，才能满足压缩感知的稀疏化要求[4-6]。基于可压缩信号的压缩感知数学模型如式(1)所示：

min‖α‖0s.t.y=ΦΨTα(x=ΨTα,ΦR=ΦΨT)

(1)

式(1)中：y是测量信号，y∈RM；Φ是测量矩阵，Φ∈RM×N；Ψ是稀疏变换基，Ψ∈RN×N；x是可压缩信号，x∈RN；α为x的稀疏变换域系数，α∈RN；ΦR为重构矩阵；M是测量矩阵的行数，N为测量矩阵的列数[7-8]。压缩感知主要分为数据采集压缩的测量阶段和数据解压恢复的重构阶段。在测量阶段，通过测量矩阵Φ采集得到测量数据y；在重构阶段，通过式(1)解算得到稀疏变换域系数α，通过逆变换从而求得信号x[3,8]。

常用的测量矩阵有高斯矩阵、哈达玛矩阵和伯努利矩阵等。这些矩阵尽管能很好满足压缩感知的约束等距性要求，但多为稠密矩阵，元素所需存储空间大[9-10]；而且由于其非结构化的本质导致计算复杂度高，不利于编程和硬件实现。对于可压缩信号，重构矩阵性能的好坏与稀疏变换基和测量矩阵有关。文献[11—12]在稀疏变换基已经确定的情况下，以列相关性最小化或平均化为目标来优化重构矩阵，得到优化后的重构矩阵。尽管经过优化的重构矩阵有更好的重构能力，但是对应的测量矩阵已不是原来的测量矩阵，实用价值不高。针对稀疏信号，基于0-1循环矩阵提出的测量矩阵优化算法实现了在测量阶段采用事先确定的测量矩阵采集测量数据，在重构阶段采用优化后的测量矩阵重构稀疏信号，取得了很好的效果[13]。

基于数字微镜(digital micromirror device,DMD)的单像素相机采用的0-1随机矩阵尽管易于硬件实现且所需存储空间小[4,14-15]，但在利于编程和运算速度方面依然不如0-1循环矩阵。离散余弦变换(discrete cosine transform, DCT)是影像和视频压缩中广泛使用的通用技术[8]。DCT除了具有正交变换性，还能很好地描述可压缩信号的相关特征。对于可压缩信号，压缩感知的重构效果不但受到测量矩阵的影响，也取决于稀疏变换基与测量矩阵的相互作用。因此，本文以DCT矩阵作为式(1)的稀疏变换基，以单像素相机的0-1随机矩阵[4,14]和0-1循环矩阵作为式(1)的测量矩阵，在验证检验矩阵优化算法通用性的同时，开展单像素相机测量矩阵的比较评估。进而理论分析稀疏变换基与测量矩阵的相互作用机理。

为便于与已有文献对比，测量矩阵大小设置为128×256。0-1循环矩阵初始行向量为32个随机分布的1，每一行向量都是前一行向量各元素右移两位的结果。0-1随机矩阵各行向量包含32个随机分布的1。

1 基于不同测量矩阵的重构矩阵优化前后的性能对比

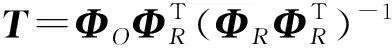
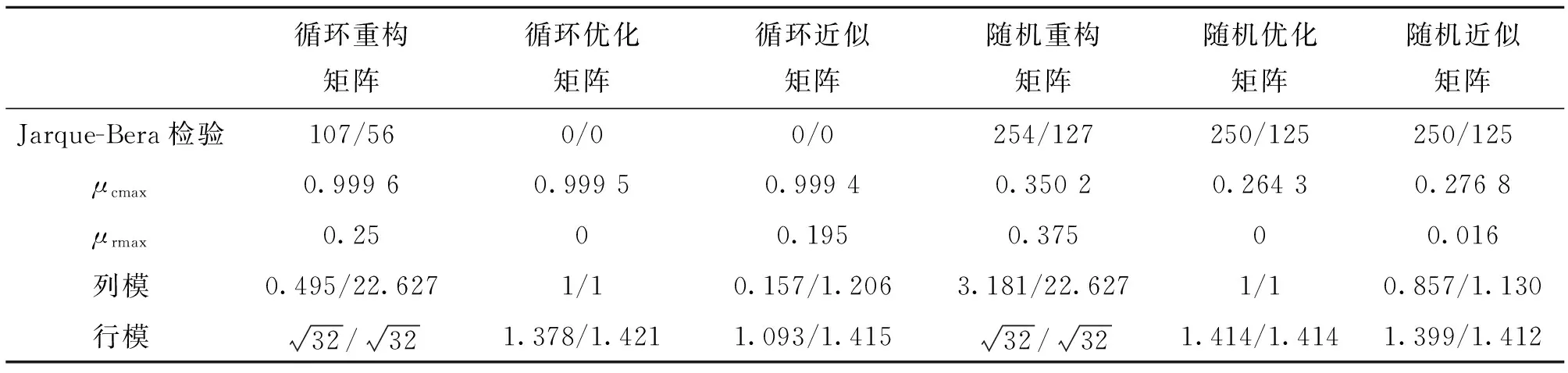
表1 6类矩阵的相关参数Tab.1 Parameters of 6 matrices

表1为测量矩阵分别采用0-1循环矩阵和0-1随机矩阵，稀疏变换基采用DCT矩阵，n=100次时相应重构矩阵、优化矩阵和近似矩阵的各种统计参数。Jarque-Bera检验这一行“/”左边的数据表示服从高斯分布的列数；“/”右边的数据表示服从高斯分布的行数。μcmax表示各列间相关系数绝对值的最大值；μrmax表示各行间相关系数绝对值的最大值。行模和列模这两行中“/”左边表示最小值，“/”右边表示最大值。

根据文献[8,13]可知，经过行向量正交规范化和列向量单位化的优化矩阵和近似矩阵的性质与高斯矩阵相近，具备高斯矩阵对各类稀疏信号的普适性。本文以此为依据，通过图1—图4比较分析循环重构矩阵和随机重构矩阵在迭代优化过程中的优化矩阵和近似矩阵的性质变化。

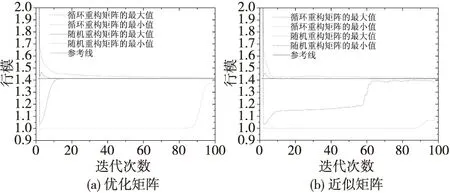
图1 基于循环重构矩阵和随机重构矩阵的优化矩阵和近似矩阵的行模极值与迭代次数的关系Fig.1 Row norms extreme value of optimization matrix and approximate matrix based on circulant reconstruction matrices and random reconstruction matrices vs. iteration

由图2(a)可知，随机优化矩阵的列相关系数绝对值最大值和行相关系数绝对值最大值在第3次迭代后收敛，列相关系数绝对值最大值接近于0.26，行相关系数绝对值最大值接近于0；循环优化矩阵的列相关系数绝对值最大值接近于1，行相关系数绝对值最大值接近于0。由图2(b)可知，随机近似矩阵的列相关系数绝对值的最大值在第3次迭代后收敛，接近于0.27，行相关系数绝对值最大值在第62次迭代后收敛，接近于0；循环近似矩阵的列相关系数绝对值的最大值接近于1，行相关系数绝对值的最大值在第95次迭代后接近于0.2。随机优化和近似矩阵的不相关性都好于循环优化和近似矩阵。

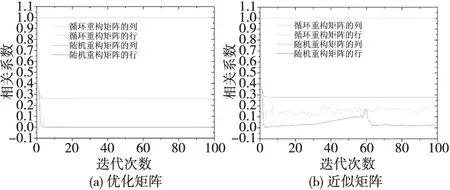
图2 基于循环重构矩阵和随机重构矩阵的优化矩阵和近似矩阵的列相关系数的绝对值最大值与迭代次数的关系Fig.2 Maximum value of absolute value of the row and column correlation coefficient of optimization matrix and approximate matrix based on circulant reconstruction matrices and random reconstruction matrices vs. iteration

由图3(a)可知，随机优化矩阵服从高斯分布的列和行在第62次迭代后收敛，服从高斯分布的列数接近于250，服从高斯分布的行数接近125；循环优化矩阵服从高斯分布的列数和行数在第2次迭代后迅速收敛于0。由图3(b)可知，随机近似矩阵服从高斯分布的列数和行数在第62次迭代后收敛，服从高斯分布的列数接近250，服从高斯分布的行数接近125；循环近似矩阵服从高斯分布的行数和列数在第2次迭代后迅速收敛于0。随机优化和近似矩阵服从高斯分布的行列数都好于循环随机和近似矩阵。

由图4可知，随机近似矩阵列模的极大值和极小值在第5次迭代后收敛，极大值接近于1.1，极小值接近于0.9；循环近似矩阵的列模的极大值在第3次迭代后收敛于1.2，最小值收敛于0.15，相差较大。随机优化和近似矩阵的列模的收敛性都好于循环优化和近似矩阵，前者更接近于1。由图1—图4可见，随机优化和随机近似矩阵的性能都好于循环优化和循环近似矩阵的性能。

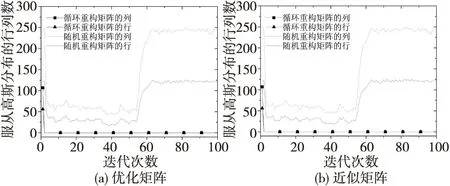
图3 基于循环重构矩阵和随机重构矩阵的优化矩阵和近似矩阵的服从高斯分布的行列数与迭代次数的关系Fig.3 Number of row and column which follows the Gaussian distribution of optimization matrix and approximate matrix based on circulant reconstruction matrices and random reconstruction matrices vs. iteration

图4 循环和随机重构矩阵的近似矩阵各列模极值与迭代次数的关系Fig.4 Column norm extremum value of approximate matrix of circulant and random reconstruction matrices vs. iteration

2 稀疏变换基与测量矩阵的相互作用

图5是循环和随机重构矩阵的灰度图。随机重构矩阵的灰度图依然保持很好的随机性；循环重构矩阵的灰度图呈左右对称结构。即使只取循环重构矩阵的左半部分或右半部分，甚至各半部分的1/4来研究，其μcmax也达到0.7，各列高度相关。测量矩阵与稀疏变换基的转置矩阵相乘就可得到重构矩阵。DCT是一种空间域的低通滤波器，可将信号从空间域转换到频率域。DCT相当于长度约是它两倍的离散傅里叶变换，是特殊的离散傅里叶变换。采用DCT矩阵作为稀疏变换基时，测量矩阵与稀疏变换基的转置矩阵相乘，在物理几何意义上等价于对测量矩阵各行作一维离散余弦变换。0-1循环矩阵是确定性矩阵，每一行向量都是前一行向量各元素循环移位的结果。各行元素顺序结构相似。重构矩阵的各行就是测量矩阵各行作离散余弦变换后的稀疏变换域系数。这些稀疏变换域系数在不同频域反映着0-1循环矩阵各行向量的顺序结构信息。从而导致循环重构矩阵各列高度相似。即使对循环重构矩阵做优化也不能提高其随机性，各列依然高度相关(如表1和图1—图4所示)。由此可见，稀疏变换基与测量矩阵的相互作用，对重构矩阵的性能有着重大的影响。0-1循环矩阵不宜和DCT矩阵组合为重构矩阵；但0-1随机矩阵可和DCT矩阵组合为重构矩阵。

图5 循环和随机重构矩阵的灰度图Fig.5 Grayscale image of circulant and random reconstruction matrices

3 基于不同测量矩阵的重构矩阵优化前后的重构效果

为进一步验证循环重构矩阵及其优化和近似矩阵的性能，分别用循环重构矩阵和随机重构矩阵及其优化和近似矩阵对高斯稀疏信号采用正交匹配追踪(orthogonal matching pursuit,OMP)算法重构。对每个稀疏度的信号在MatlabR2015b中重复试验500次，计算准确重构概率，如图6所示。

当测量矩阵为0-1随机矩阵时，随机优化矩阵和随机近似矩阵的信号重构概率明显好于随机重构矩阵；当测量矩阵为0-1循环矩阵时，循环优化矩阵和循环近似矩阵的信号重构概率不但不明显好于循环重构矩阵，而且3个矩阵的重构概率都小于1。

图6 6种矩阵的信号准确重构概率与稀疏度关系Fig.6 Prob. of exact recovery vs. the sparsity by 6 matrices

4 结论

基于DMD的0-1循环矩阵易于编程和硬件实现，但是当单像素相机采集可压缩信号时，测量矩阵与稀疏变换基相互作用，导致重构矩阵性能很差，即使使用矩阵优化算法也不能有效改善其性能。对比分析了以DCT为稀疏变换基的基于0-1随机矩阵和0-1循环矩阵的重构矩阵，及其优化前后的重构效果。研究发现：单像素相机不能使用0-1循环矩阵作为测量矩阵，可使用0-1随机矩阵作为测量矩阵，并能对相应重构矩阵做有效优化。同时给出了测量矩阵和稀疏变换基作用机理的理论解释。为单像素相机测量矩阵的选型和设计提供了方向指导，利于设计制造出性能更优的单像素相机。