圆的面积公式推导的再思考

王广强

【摘要】现在的数学教学不仅仅是数学知识的传授，更应关注数学思想方法和数学文化的渗透.新课程标准中提出了三大基本思想：抽象、推理、模型.圆的面积推导过程就是将圆转化成我们已经学习过的长方形、三角形或梯形，再利用已有的旧知识解决新问题.该过程能有效地渗透数学思想，发展学生的推理能力和创新意识.

【关键词】圆的面积;数学思想;转化思想;极限思想

“圆的面积”是小学数学教学中非常重要的一课，本节课不仅可以体现数学中非常重要的思想方法，还有利于培养学生的创新能力和探究意识.

新课程标准指出，数学教学要培养学生的“四基”，即基础知识、基本技能、基本思想和基本活动经验，而基本思想指：抽象、推理和模型.

人教版课本是通过分割、转化，将圆的面积转化成平行四边形，进而转化成长方形进行推导的，过程如下.

在硬纸上画一个圆，把圆分成若干（偶数）等份，剪开后，用这些近似于等腰三角形的小纸片拼一拼，你能发现什么？（图1）

分的份数越多，每一份就会越小，拼成的图形就会越接近于一个长方形.（图2）

通过观察，我们可以看出圆的半径是r，长方形的长近似于圆的周长的一半，宽近似于半径.因为长方形的面积=长×宽，所以圆的面积=周长的一半×半径=C2×r=πr2，即圆的面积公式是S=πr2.

在上述的过程中，渗透了转化的数学思想，将未知的圆转化成平行四边形，再由极限的数学思想，将平行四边形近似地看成长方形，而后又由变与不变的数学思想，将长方形的面积与圆的面积沟通起来，最终得出圆的面积计算公式.在整个推导过程中始终渗透了推理的数学思想.

冀教版教材在利用上述方法推导圆的面积公式之前，又采用了以下的方法让学生初步感知圆的面积计算公式.

把一个半径是10 cm的圆形飞镖板平均分成20份，估算一下一块飞镖板的面积，如图3.

我们可以将每一份飞镖板近似看成底是圆的周长的120、高是10 cm的等腰三角形，通过计算我们可以得到一份飞镖板的面积约是2×3.14×10×120×10÷2=15.7（cm2），所以圆的面积就是20×15.7=314（cm2）.

在此基础上如果将飞镖板的半径用字母r表示，将飞镖板平均分成n份，我们不难推出圆的面积公式是S=2πrn×r÷2×n=πr2.

在上述的推导过程中，我们利用了极限的思想，分得份数越多，每一份就越接近一个三角形.我们还利用了转化的思想，将圆的面积转化为三角形的面积进行求解.

我们看到，不论是人教版还是冀教版教材，在推导过程中，都是将圆平均分推导出来的，除了以上的推导方法，我们还有其他的方法吗？答案是一定的，但是无论怎样进行推导，其基本思想是不变的.

我们还是按照平均分的思路，如果不像第一种方法那样拼，我们把第一行放1个，第二行放3个，第三行放5个，第四行放7个，这样也恰好可以拼成三角形，如图4.

所拼得的三角形的底是圆的周长的14，高是4r，我们不难推出圆的面积为S=C4×4r×12=12Cr=πr2.

当然，稍加思考，我们可以将其拼成一个梯形，如图5.

所拼得的梯形是上底是圆的周长的316，下底是圆的周长的516，高是2r，我们也不难推出圆的面积为：S=3C16+5C16×2r×12=12Cr=πr2.

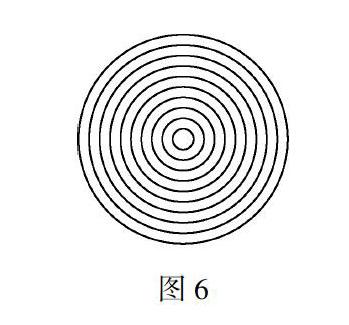
我们现在将圆进行如下分割，在一个圆中作出它的同心圆，并使它们的半径成等差数列，即相邻的两个圆的半径之差（环宽）相等，如图6所示.

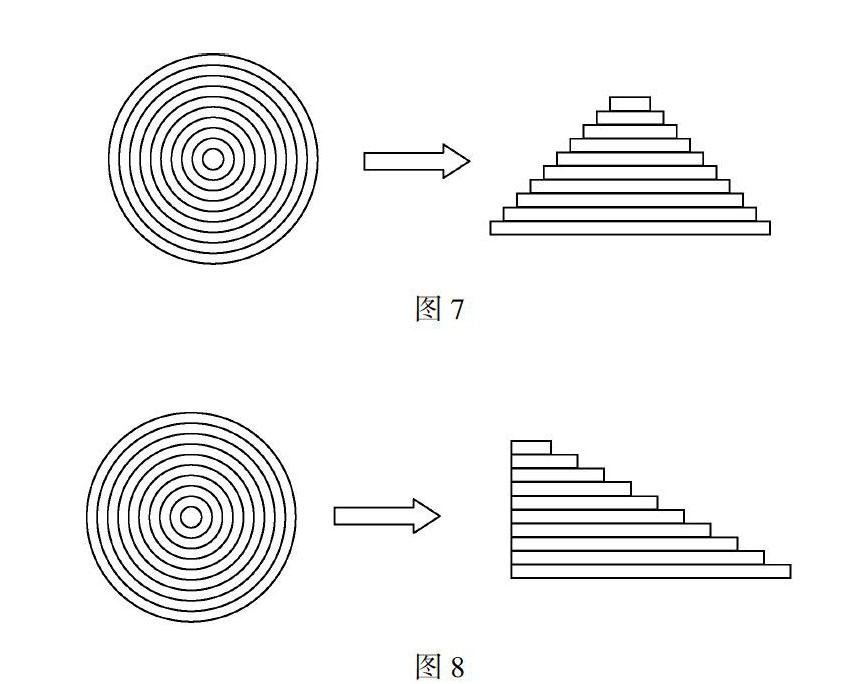
我们将这些同心圆沿线剪开，可以近似得到以下两种不同的图形（图7，图8）.

图7是等腰三角形，三角形的底是圆的周长，高是半径，所以圆的面积=三角形的面积=C×r×12=πr2.

图8是直角三角形，直角边分别为圆的周长和圆的半径，所以圆的面积=三角形的面积=C×r×12=πr2.

到此，大家可能觉得圆的面积公式的推导方法已经很多了，其实还有很多，比如我们可以把圆看作正n边形，通过求n边形的面积，最终通過求极限得到圆的面积，还可以通过微积分推导圆的面积公式.

圆的面积公式推导方法可能还有很多，但是我们可以总结两点：一是利用转化，将曲线型图形转化成直线型图形（其实平面图形的面积推导都是转化成已知图形得到的），二是利用高等数学中极限和微积分的知识推导.