习题资源的开发和利用
余亚萍

【摘要】教学中,经常会出现一道习题反复讲解但学生却反复出错的情况.是什么导致学生反复出错?应该如何利用这道习题?这值得教师深入研究、分析,充分挖掘习题资源,锻炼学生思维.
【关键词】习题资源;思维;课堂
习题能够帮助学生巩固新知,发展实践应用能力.教师应充分挖掘习题资源,利用习题课堂启迪学生思维.北师大版数学教材习题和相关配套练习内容丰富,不仅包含基础知识和基本技能,还蕴含丰富的数学思想方法,是学生学习和教师教学的重要载体.然而,很多教师在选择、分析习题时存在一些误区,导致一道习题反复讲解,反复强调,学生却反复出错的情况常有发生.
【问题呈现】
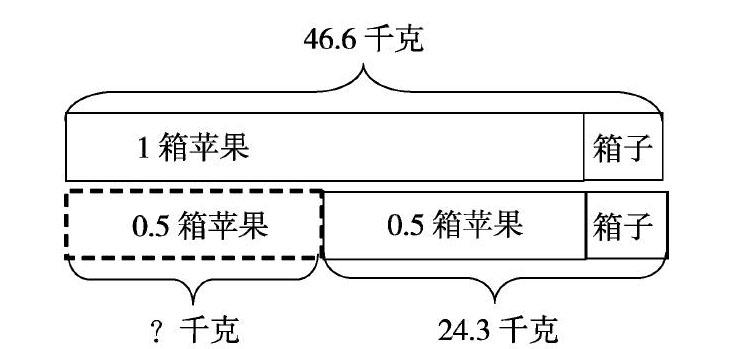
北师大版数学四年级下册第一单元有一道课后习题:一箱苹果的质量(含箱子)是46.6千克,倒出一半苹果后的质量是24.3千克,全部苹果的质量是多少千克?箱子的质量是多少千克?
通过调查发现,在独立完成的情况下,学生出错率高达70%,经过教师分析讲解之后,学生独立完成作业本中的类似题目时,出错率还是高达60%.除去学生自身因素外,教师分析讲解此题的思路和方式也值得探究.笔者通过访谈教师,观察课堂,发现大部分教师的处理方式是:独立思考完成,学生汇报交流,教师归纳总结,课后完成练习.
解题思路:
1箱苹果+箱子=46.6千克 ①
0.5箱苹果+箱子=24.3千克 ②
部分教师还会附上示意图:①-②,得
1箱苹果+箱子-0.5箱苹果-箱子=46.6千克-24.3千克,
所以,1箱苹果=44.6千克,箱子=2千克.
用图形帮助学生理解题意,做题正确率会高很多.但在实际做题时,能自觉画图理解题意的学生少之又少
,大部分学生都是凭空想象.虽然后续通过不断练习、讲解、巩固,大部分学生能解决此类题目,但是这样低效的讲解是否对学生有益?传统的习题教学课堂是否缺少些什么呢?
反思:这样的习题课导致了学生的一知半解.
开始的独立思考环节(3~5分钟),有的学生还没有进入状态,但在个别有思路的学生迫不及待想分享成果、教师追求高效课堂目的的驱动下,时间一到,教师就会组织学生汇报交流.很多学生本身存在畏难情结,就会坐等其他同学的讲解.这样的汇报交流流于表面,即使有10分钟的时间学生也难以深入.教师根据汇报会有2~3分钟的总结概括,最后预留5~7分钟的练习时间.虽落实了单个知识点,但学生对此常态习题课却缺乏兴趣,导致后面反复出错.
这样的课堂是否应该引起教师的反思:①习题课应该采取什么方式激发学生兴趣,引导学生真正理解解题思路?②通过解决一道题,学生能由点及面构建链状知识点吗?③如何培养学生的数学思维,提升学生的核心素养?
【教学实践】
(一)回顾旧知,探索思维起点
1.复习铺垫,溯源头
这类文字题对学生而言是抽象的、难以理解的,所以有些教师辅以图形示意图帮助学生理解,但学生却还是凭空想象.难道是因为没有图形经验的积累,所以导致学生不会迁移吗?实际上,第一学段练习中经常会出现有趣的图形数字题,所以教师可以先出示简单图形数字题,唤起学生的旧知,为新知学习做好铺垫.这部分习题一定要有“说一说自己思路”的活动要求.
3.反思总结,寻方法
师:同学们解题的速度非常快.请大家再仔细观察一下这三组题目,并回顾刚刚的解题过程,有哪些相同之处呢?
生:每一组题都是通过上下两道题联合解决的,其中一题都是通过另一题代入解决的.
生:都要找到上下两题的相同部分,这是解题的关键.
……
师:同学们非常善于观察,而且总结很到位,其实我们已经在运用代入、合并、消元等方法来解题了.
(二)学以致用,探寻相通点
1.体会数形结合
师:那这些图形题和我们今天要解决的问题有什么联系呢?请同学们仔细观看课件.
2.感受符号简洁
师:你还能写出更简洁的图形算式来表示这道题吗?
学生成果:
师:老师发现同学们都很聪明,那这三种表达式有哪些相同之处?
生:除了第二组图形,其他算式都用数字表示有几个图形.
生:但是第二组其实已经用图形表示出“半个”这个数字了.
生:其实也可以用别的图形表示.
师:真的非常佩服同学们的观察力和思维能力,连蕴含的数字都看出来了,还能想到用其他图形进行替换,太棒了!现在,你能把前面独立练习的题也写得更简洁吗?
学生成果:
(三)巧设迁移,开拓学生思维
1.同类题型,自主解决
师:刚刚有同学说用其他圖形也可以表示苹果和箱子,除了图形,你还能用什么来表示呢?
生:可以用文字.
生:我觉得用文字还不如用图形.
……
生:可以用字母表示.
在教师的不断引导下,学生的思维更加发散,逐步由直观的苹果图形抽象出其他图形,再抽象出字母.可在此基础上辅以相应的练习,巩固符号化思想.
2.学以致用,迁移解题
学生经历了一系列归纳活动之后,体会到了运用数形结合的方法可以使抽象问题直观化,运用符号可以使复杂问题简单化,此时教师应进一步强化学生的这一解题思路.
强化练习:
一桶油连桶重32.5千克,倒出一半油后,连桶重17.5千克.油的质量是多少千克?桶的质量是多少千克?
3.提升练习,拓展思维
如果仅停留在模仿思考层面,那么学生的思维能力得不到提升和发展,所以需要设计不同类型的题目,指导学生找出知识点之间的内在联系,由点及面,构建链状知识网,使学生的思维走向深处.
拓展练习:
(1)小明语文、数学两科的平均成绩为90分,加上英语成绩后,平均成绩提高3分.小明的英语成绩为多少分?
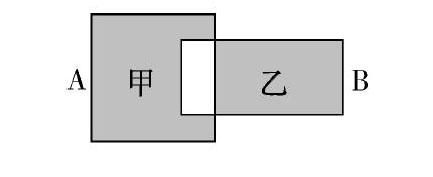
(2)正方形A的边长为5厘米,长方形B的长为6厘米,宽为3厘米,现在把它们如下图那样重叠放置.涂色部分甲比涂色部分乙大多少平方厘米?
学生按照活动要求独立完成、交流反馈之后,回顾:这两题哪个量是不变的?和之前题目有哪些相同之处?
教师利用课件引导,第一题的关键是语数成绩前后是不变的,第二题的关键是重叠部分是不变的.
语+数=90×2=180
语+数+英=(90+3)×3=279若语+数=a[]
英=ba=180
a+b=279
A=甲+空=5×5=25
B=乙+空=6×3=18甲-乙=A-B
以上两题都有一定难度,在有限的课堂时间限制下,教师可以要求学生只写出解题思路,同桌交流后,教师出示课件进行指导,学生课后再进行具体计算.从基础题到变式题,再到拓展题,循序渐进,既适应学生的思维特点,又为不同程度的学生提供了更多的发展可能.
【教学思考】
教学用书和配套练习册中其实隐藏着许多好题,如果教师能挖掘习题的拓展功能,灵活设计习题课,就能放大习题的教学价值.那么教师在教学中该如何发挥习题的这些功能呢?
(一)深挖教材文本资源
教材不仅有数量合适、形式多样的课后习题,还有拓展性题目,兼具巩固基础和拓展思维的功能,能够满足不同层次学生的需求.教师在备课时,不仅要着眼于本册教材前后联系,还要兼顾整个学段知识点的前后联系.
如本案例中“苹果和箱子”这一题虽是课后习题,和第一学段的图形题却有着相同的解题思路,所以利用图形题复习导入,将“数”和“形”有机结合,找到知识点间的前后联系,大大降低了题目难度.若仅停留在这个层面,此题的价值还没有达到最大化,而通过用字母替换图形,将本册后续第五单元“认识方程”的内容又提前和本单元建立联系,为后续二元一次方程组的学习做了铺垫.
(二)充分利用课堂资源
如本案例中,教师利用课件演示示意图和图形算式间的联系,在课堂不同阶段的任务要求中反复出现“说一说自己的思考过程”“有哪些相同之处”的提问,其实就是引导学生不断观察、比较、反思、总结.学生由简单问题找到思考的切入点,然后上升到复杂问题突破思考的难点,克服不同高度障碍的同时也在提升思维能力.这样充满挑战的课堂才能引起学生的兴趣,激发其学习动力.
(三)构建自我思维
学生思维能力的形成不可能一蹴而就,而在于一朝一夕的积累,循环往复的训练,更需要教师逐步渗透思维方法.
如本案例开始的“复习旧知”环节,教师先要求学生说一說自己的思考过程,在学生求出三组题目的○和☆后,紧接着抛出“有哪些相同之处”的问题引导学生进行反思总结,让学生找到思维的起点.课堂推进到“学以致用”环节,先让学生找相通之处,再通过课件演示进一步明确题目、直观图、表达式之间的相通之处,为学生深入思维提供支点.最后用字母代替图形,抽象出代数式,使学生思维从具体走向抽象,从感性到达理性,为思维的发展提供更广阔的空间.
【参考文献】
王雪飞,戴银杏.加强习题研究 提升命题能力:一道习题的教学实践与思考[J].教学月刊·小学版(数学),2019(12):19-23.

