有数学味的“折纸中的相似问题”再探讨
赵正萍
【摘要】“折纸中的相似问题”这一课例,折射出了一节“数学味”浓的数学实验课教学主要是通过操作、观察、抽象、分析、归纳等思维活动获得数学结论的.这一课例让一张纸产生了教学价值,使学生体验到了数学的学习从“听”数学变成了“做”数学,从“被动接受”变成了“主动探究”.学生通过“做”数学实验体验发现的乐趣,感悟数学的真谛,发展数学思维,提高自身在实践中解决问题的能力和创新意识,逐步积累数学活动经验.
【关键词】折纸;数学实验;操作观察;数学建模
案例背景:
对于数学实验而言,许多学者给出了不尽相同的界定.曹一鸣认为,数学实验是指实验者为获得某种数学理论、检验某个数学猜想、解决某类数学问题,运用一定的物质手段,在数学思维活动的参与下,在典型的实验环境中或特定的实验条件下所进行的一种数学探索活动[1].数学实验课就是为“数学实验”搭建的平台,是“数学实验”的数学环境,是激发学生数学思维的催化剂,是数学探索活动的一种新的模式,让学生从有意义的接受学习,转变为有意义的发现学习.
有效的数学学习活动不能单纯依赖模仿和记忆,动手实践、自主探索与合作交流才是学生学习数学的重要方式.《义务教育数学课程标准(2017年版)》提出:教师要结合教学内容,落实“双基”走向“四基”,培养“两能”发展为“四能”,促进学生数学学科素养的发展.数学活动经验的积累是提高学生数学素养的重要标志.数学活动经验需要在“做”的过程和“思”的过程中积淀,是在数学学习活动过程中逐步积累的.
教师在教学“折纸中的相似问题”这节课时,不能假借折纸操作,将本课上成一节只用相似解题的课,也不能上成只让学生折纸的劳技课,而是要通过问题串让学生学会运用折纸呈现出折叠类问题,同时构建相似问题的数学模型,要将这节课上成一节数学实验与数学思维并存、有“数学味”的实验课.
案例描述:
师:折纸可以产生全等图形,那么会不会产生相似图形呢?
活动一 任意三角形纸片的折纸
问题1.出示一张三角形纸片,请你通过折纸的方式,将∠A翻折,折痕为DE,A点的对应点为F点.
师:观察翻折前后产生了哪些相等的量?
生:A点可能落在形内、形上、形外.DA=DF,EA=EF,∠ADE=∠FDE,∠AED=∠FED,∠A=∠DFE.(学生通过动手操作立即发现A点翻折后的位置有三种不同情况)
师:线段AF与线段DE有什么关系?
生:根据轴对称的性质:对应点的连线被对称轴垂直平分,即DE垂直平分AF.
师:能通过折叠,使图形中产生相似的三角形吗?
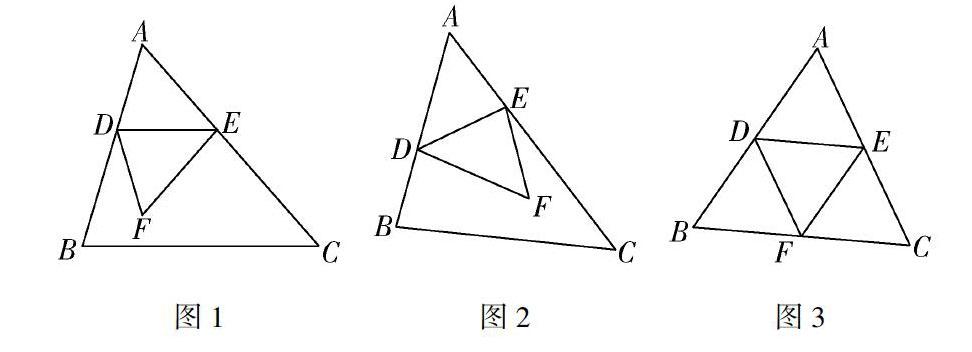
生:折成“平行相似”型(图1)或折成“斜交相似”型(图2).(学生折出不同的折痕)
师追问 :当折成平行相似中的A型相似时,怎样折DE一定平行BC?
生:折成平行相似中的A型相似时,先折出高线AF,再对折,使点A与点F重合,这时折痕DE平行于BC.
在这一环节中,学生通过动手操作参与到学习中,通过观察获得感官刺激,感悟到折纸中蕴含的轴对称变换知识.其次,学生折纸产生相似三角形,在头脑中出现相似三角形基本图形,通过动手操作找出相似模型,直观形象.教师的追问再一次让学生把折纸与数学知识联系在了一起.
师:折叠时,如果A点落在边BC 上(如图3),那么△BDF和△CEF 一定相似吗?
生:不一定.
师:怎样改变图形的形状可以实现△BDF和△CEF 相似呢?
学生自然想到需要改变△ABC的形状,引出活动二,过渡自然,调动学生的学习兴趣.
活动二 特殊三角形纸片的折纸
问题2.将问题1中纸片的形状改为等边三角形,点A恰好落在BC边上的点F处,△DFB与△CEF相似吗?
师:折一折,观察并找出图中所有的相似三角形.
图4生:折成图4,F是BC上任意一点时,△BDF∽△CFE,△ADE∽△FDE(且全等).
师:想一想,如果图中四个三角形两两都相似,那么折痕DE需要满足什么条件?(学生讨论、交流发现:DE是等边三角形ABC的中位线且A点的对应点F在BC的中点处)
师追问:如果△ABC为等腰直角三角形,△DFB与△EFC仍然相似吗?需要满足什么特殊条件?(学生有了前面的学习经验,通过动手操作即可找出答案)
活动三 矩形纸片的折纸
师:刚刚研究了折叠三角形纸片产生的一些相似情形,如果翻折四边形纸片能否产生相似三角形呢?哪种四边形通过翻折产生相似三角形的可能性更大呢?
生:矩形.
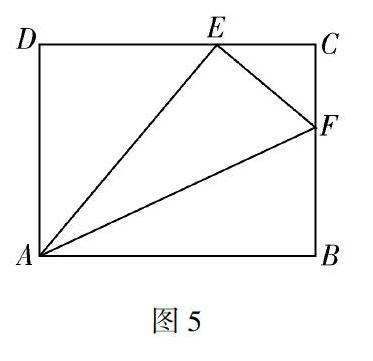
图5问题3.如图5,一张矩形(非正方形)的纸片ABCD,把∠B沿AF对折,使点B恰好落在CD边上的点E处.
师:请同学们按照要求,翻折准备好的纸片,找出图中的相似三角形.
生:△EAF∽△BAF(且全等),△DAE∽△CEF.(一张矩形纸片中∠B翻折后的位置也有三种情况,对点B落在边上的特殊情况进行探究学习,操作后学生立即看出了“一线三等角”中的相似模型)
师追问1:图5中这四个直角三角形一定两两相似吗?
生:不一定.
师追问2:要使这四個直角三角形任意两个都相似,四个直角三角形中的锐角应满足什么条件?
生:四个直角三角形中的最小锐角是30度.
师追问3:满足上述条件的四个三角形相似时,矩形长和宽的比是多少?(小组讨论)
生1:通过设K法,设CF=x,运用勾股定理等知识求出了长∶宽=AE∶AD=2∶3.
生2:运用锐角三角函数求出ADAE=cos 30°=32.
师追问4:此时,E点在什么特殊位置?
生:E在CD的中点处.
师追问5:你能将手中的纸片通过折叠、度量或其他方法裁剪出符合上述要求的矩形吗?(学生想出了两种方法)
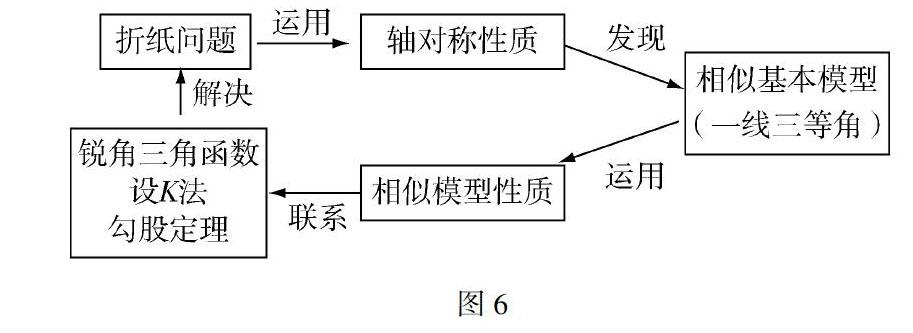
在这一环节中,学生通过折纸找出“一线三等角”中的相似三角形模型,用所学的知识找出了四个直角三角形出现两两相似时,纸片长与宽的比值要求.教师又追问:一张矩形纸片怎样折可以满足上述要求?其实怎样折,就是在矩形纸片中构造出等边三角形ABE.出乎意料的是学生有不止一种的折纸方案.一节课在折——探——折中,进行了折纸问题解决方案总结(图6).
案例反思:
1.折纸为学生提供了实验探究学习的平台
整节课从最基本的三角形入手,通过问题串的层层逼近,让学生在折纸中感悟相似,让学生经历由简单到复杂、由特殊到一般的探索过程.从一般三角形到特殊三角形(等边三角形和等腰直角三角形),再从一般四边形到特殊四边形(矩形)的过程,让学生深刻领会折叠的本质是轴对称,而轴对称的本质是图形全等的不变性,涉及利用勾股定理列方程、相似中的一线三等角模型、特殊角的三角函数等核心知识和方法,对学生“动态变化、数形结合、逻辑推理、数学计算与数学建模”等数学素养的提高产生了积极影响.
2.实验操作中的启发
实验操作是培养学生观察想象和逻辑思维能力的重要途径.学生通过观察可以猜想数学结论,通过操作可以验证逻辑推理得到的结论,还可以通过操作发现模型,运用所学知识解决问题或固化数学结论.学习折叠类问题的基本策略流程是:实验操作——观察猜想——推理论证——建模求解.因此,数学实验课的设计一定要有立意,必须建立在思维活动上,如果离开了数学思维活动,数学实验课就会变成一节按实验程序操作的活动课,这样就失去了数学味道,偏离了数学实验课教学的轨道.
3.提升了学生的数学素养
“折纸出发——找相似三角形——回到怎么折”这一过程,通过数学问题的诱发,从操作开始,最后又回到操作上,让学生边折边发现,将操作活动与想象、抽象、推理、计算联系在一起,让学生的大脑发挥寻找、验证、构建等功能,激发学生的创新意识,让学生在思考和提问中合作、讨论、交流、实现数学思维与数学方法的自我完善,使学生在数学技能和数学思维得到发展的同时,自身数学素养也逐步提升.
4.给教师教学的启示
折叠型操作问题就是运用轴对称变换的性质解决问题,一直是中考的热点.单独提到轴对称的性质,学生大多能够理解和掌握.但具体到某些现实情境时,学生常常会感到困惑,其主要原因是学生不能把折叠问题快速转化抽象出对应的数学模型,不会将数学问题进行直观化的理解和设计.针对这种情况,在今后的教学中,教师要舍得花时间,让学生通过动手实验完成知识的学习,给学生充足的时间和空间,让他们动手做、动手画,让学生体验数学的乐趣.学生在“做”中学,在思中“悟”,体验到数学学习在变“听”数学为“做”数学,变“被动接受”为“主动探究”.学生通过“做”数学实验体验发现的乐趣,感悟数学的真谛,发展数学思维和智慧,提高实践能力和创新意识,逐步积累数学活动经验[2].
【参考文獻】
[1]曹一鸣.数学实验教学模式探究[J].课程·教材·教法,2003(01):46-48.
[2]喻平,董林伟.初中数学实验的本质解析[J].课程·教材·教法,2016(08):89-95.

