Post Crash模型下障碍期权定价的有限差分方法
何桃顺, 李沁林, 刘 淞
(内江师范学院 a.四川省高校数值仿真重点实验室 b.数据恢复四川省重点实验室 c.数学与信息科学学院, 四川 内江 641100)
0 引言
障碍期权是金融市场中一种极其常见的路径依赖期权,其最终收益不仅取决于标的资产在期权到期日的价格,而且还与标的资产价格在整个期权有效期内是否达到某一规定水平(障碍值)有关.按照标的资产达到规定障碍后的期权状态,障碍期权可分为敲出期权和敲入期权.敲出期权是指当标的资产的价格达到规定障碍时终止有效的期权,而敲入期权是指当标的资产的价格达到规定障碍才开始有效的期权.根据标的资产价格上升和下降达到规定障碍的情形,障碍期权又可分为上升障碍期权和下降障碍期权.除此之外,每一类障碍期权都可以分为看涨和看跌两大类,因此障碍期权可细分为八大类,具体可参考文献[1]和[2].由于障碍期权的价格要比标准欧式期权的价格便宜,所以障碍期权备受市场投资者的青睐,因此合理地对障碍期权进行估值就成为国内外学者研究中的重要课题.这方面的开创性工作源于1973年Merton[3]在标的资产价格遵循几何布朗运动模型的假设下推导了障碍期权的解析定价公式;随后,Wong等[4]将其扩展为多资产的情形,推导了几何布朗运动模型下多资产障碍期权的解析定价公式.实证研究表明,虽然在平稳的金融市场环境中几何布朗运动能很好的模拟股票价格变化,但是几何布朗运动不能有效的捕捉市场波动率所呈现的“微笑”特征,也不能反映股价对数收益率所表现出的“尖峰厚尾”统计分布特征.为了弥补利用几何布朗运动刻画股价变化存在的缺陷,许多专家学者在股价模型改进方面做出了许多有价值的探索,研究了常弹性方差模型[5]、Hull-White模型[6]、Heston模型[7-8]以及跳扩散模型[9]下的障碍期权定价问题.由于复杂金融市场模型下的障碍期权通常没有解析定价公式,所以国内外学者提出了利用二项式定价方法[10]、有限差分方法[11-13]和傅里叶余弦方法[14]等数值方法计算障碍期权的价格.
另一方面,许多学者对金融危机爆发后的金融市场动态进行了实证研究.如:Lillo等[15]研究发现金融崩溃后的金融市场服从幂律松弛衰减规律;Sornette[16]研究表明金融崩溃后的金融市场动态遵循收敛的振荡运动.基于上述实证研究结果,Dibeh等[17]在Black-Scholes模型的基础上将崩溃后的市场指数耦合到单个股票价格的动态过程中建立了如下Post Crash期权定价模型:
dSt=(μSt+bg(t))dt+(σSt+γg(t))dWt,
(1)
其中,St表示股票在t时刻的价格,μ和σ分别表示股票的原始收益率与原始波动率,Wt表示标准的布朗运动,b和γ都是常数分别刻画市场指数对股票收益率和波动率的影响程度,g(t)表示S&P500指数施加的一个强制函数,它可以表示Sornette对股市指数在市场崩盘后的经验拟合,通常表示为如下指数衰减的正弦函数:
g(t)=α+βeptsin(ωt).
Dibeh等在上述Post Crash期权定价模型(1)下利用Δ对冲的方法推导了欧式期权价值函数满足的偏微分方程,然后采用有限差分方法对其进行数值求解得到该期权的价格,并将其计算结果与直接利用蒙特卡洛模拟方法计算的期权价格进行了比较;Luo等[18]考虑了Post Crash期权定价模型下的美式期权定价问题,他们采用无套利定价原理推导了美式期权价值函数满足的偏微分方程并用惩罚方法对其进行数值求解;El-Khatib等[19]将Post Crash期权定价模型扩展为带跳情形并讨论了该扩展模型下的欧式期权定价问题.除此之外,El-Khatib等[20]研究了Post Crash期权定价模型下资产为外国货币的欧式看涨期权与看跌期权的估值和对冲问题.
鉴于此,本文从偏微分方程的角度利用有限差分方法研究Post Crash模型下障碍期权的定价问题.然后通过数值模拟说明Crank-Nicolson差分方法的有效性和分析金融危机的爆发对障碍期权价格的影响.
1 障碍期权价值函数的偏微分方程推导
下面利用Δ对冲方法推导向上敲出看涨障碍期权的价值函数在Post Crash模型下满足的偏微分方程及边界条件,得到如下定理:
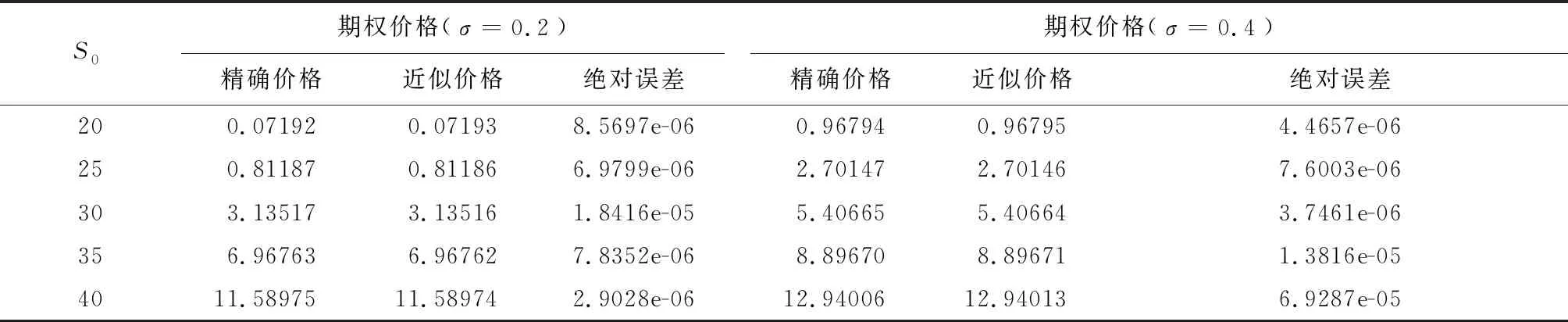
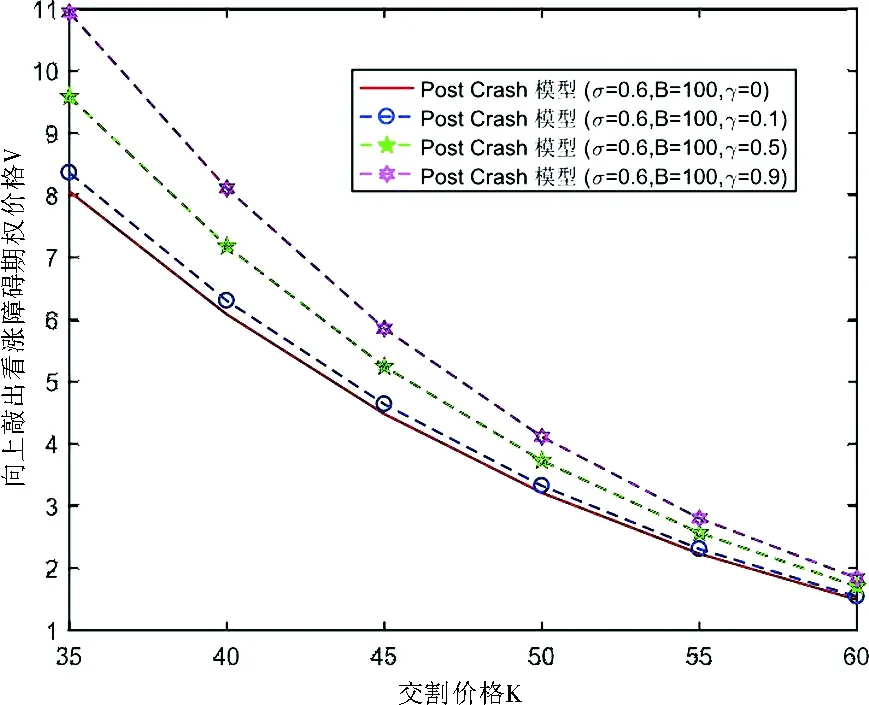
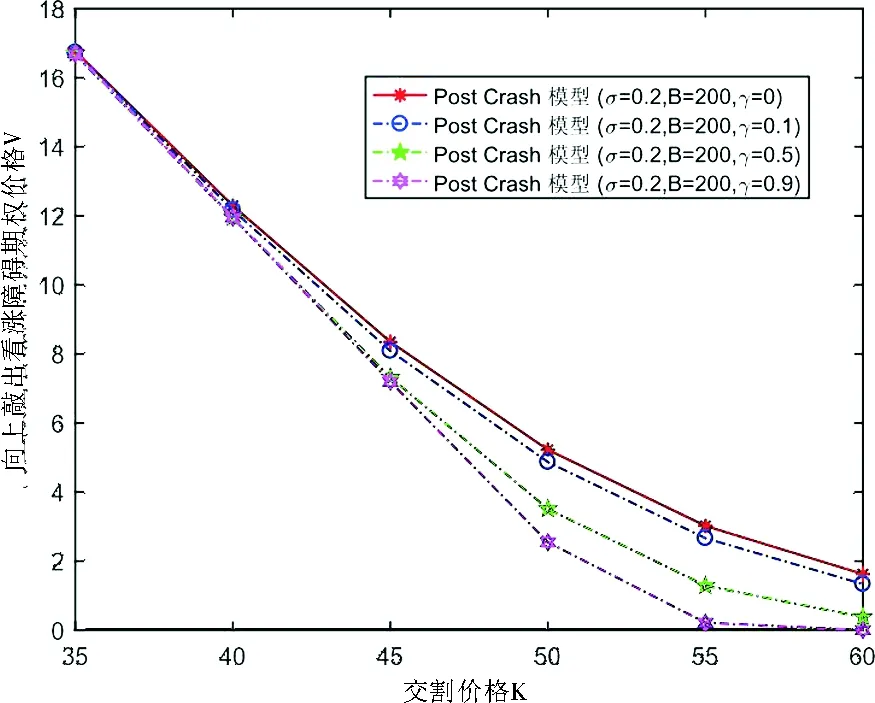
定理1设向上敲出看涨障碍期权在时刻t之前未敲出,且其敲定价格为K以及向上敲出障碍为B,股票在时刻t的价格为St=S.如果用V(t,S)表示Post Crash模型下向上敲出看涨期权在时刻t的价格,那么V(t,S)在矩形区域{(t,S);0≤t (2) 并且满足边界条件: V(t,0)=0,0≤t≤T, (3) V(t,B)=0,0≤t (4) V(T,S)=(S-K)+,0≤S≤B. (5) 证明在时间区间[0,T]上考虑一个动态投资组合,该投资组合包含一个价值为V(t,S)的向上敲出看涨障碍期权和数量为-Δt份的股票,若记投资组合在时刻t的价值为∏t,则有: ∏t=V(t,S)-ΔtSt, 进而有: d∏t=dV(t,S)-ΔtdSt. 若设无风险利率为r,由Δ对冲原理可知,构造的投资组合是无风险的,即有: dV(t,S)-ΔtdSt=r∏tdt=r(Vt-ΔtSt)dt, (6) 根据伊藤引理并联合股票过程St遵循的随机微分方程(1)可推得: (7) 将(7)式代入(6)式并整理可得: (8) 因为等式(8)右端是无风险的,所以等式(8)左端随机项dWt的系数必为0,即选取 将其带入(8)式得到: 最后根据向上敲出看涨障碍期权的特点为其设置如下边界条件,具体可参见文献[2]: 即定理1得证. 注1由向上敲出看涨障碍期权满足的偏微分方程(2)可知,当γ=0时,偏微分方程(2)变为股价过程遵循几何布朗运动(geometric brownian motion,GBM)的情形.即对金融衍生品定价而言γ=0意味着Post Crash模型退化为GBM情形而与模型参数b的取值无关. 并且满足边界条件: ∞. (9) 并且满足如下初值和边界条件: (10) (11) (12) 然后在有限区域[0,T]×[0,B]上,分别定义如下关于时间和空间的一致网格: Sj=jΔS,j=0,1,…,J;ζn=nΔζ,n=0,1,…,N. 接下来,分别定义 (13) 初值条件和边界条件相应的离散为: 本小节主要列举了两个数值算例,其中第一个数值算例用来阐明Post Crash模型下障碍期权定价的Crank-Nicoloson差分方法的有效性;第二个数值算例主要通过分析模型参数对期权价格的敏感性从而说明金融危机的爆发对障碍期权定价的影响. 在下列数值算例中,假设Post Crash市场指数函数表示为g(t)=α+βeρtsin(ωt),其 中α=-10,β=5,ρ=-2,ω=10,该函数的设置及系数的选取具体可参见文献[17]. 例1假设股价模型(1)中的模型参数γ=0,这意味着Post Crash模型简化为GBM模型.在该股价模型下,向上敲出看涨障碍期权有如下解析定价公式(参见文献[1]): (14) 式中,τ=T-t,Φ是标准正态分布函数,并且δ+(τ,S)和δ-(τ,S)分别为: 设置模型参数为r=0.05,T=1,K=30,B=200,σ=0.2或0.4,在利用Crank-Nicoloson差分方法计算期权值时还需设置参数N=400,J=3000.下面分别利用Crank-Nicoloson差分算法(13)和解析定价公式(14)计算向上敲出看涨障碍期权的价格得到表1,其中表1中的近似价格和精确价格分别为Crank-Nicoloson差分算法(13)和解析定价公式(14)的计算值,绝对误差为近似价格与精确价格之差的绝对值.由表1中的绝对误差可知,利用Crank-Nicoloson差分方法计算Post Crash模型下向上敲出看涨障碍期权的价格非常精确,从而说明该数值方法是有效的. 表1 Post Crash模型下向上敲出看涨障碍期权的价格计算结果比较 例2为了分析金融危机爆发对向上敲出看涨障碍期权定价的影响,设置参数为r=0.05,T=1,S0=50,N=400,J=3000.利用Crank-Nicoloson差分方法计算Post Crash模型下向上敲出看涨障碍期权的价格,其数值结果呈现为图1和图2.图1表明当波动率σ很小且障碍B比较大时,金融危机的爆发使得向上敲出看涨障碍期权的价格系统性的偏小;图2表明当波动率σ很大且障碍B比较小时,金融危机的爆发使得向上敲出看涨障碍期权的价格系统性的偏大.这是因为耦合了崩溃后的市场指数的股价模型使得波动率系统性的偏小以及股价一旦达到障碍则向上敲出看涨障碍期权的价格立即变为0.另外,图1和图2还表明随着模型参数γ的增加崩溃后的市场指数对向上敲出看涨障碍期权的价格影响越大.特别地,当γ越接近0时,向上敲出看涨障碍期权的价格越接近GBM模型下该期权的价格,这与预期的理论结果一致. 图1 Post Crash 模型下向上敲出看涨障碍期权的价格和交割价格之间的关系(高波动率、低障碍情形) 图2 Post Crash 模型下向上敲出看涨障碍期权的价格和交割价格之间的关系(低波动率、高障碍情形) 本文从偏微方程的角度利用Crank-Nicoloson差分方法讨论了Post Crash模型下障碍期权的定价问题.数值结果表明:利用Crank-Nicoloson差分方法计算Post Crash模型下向上敲出看涨障碍期权的价格是可行和有效的;耦合了Post Crash市场指数的股价模型使得波动率系统性的偏低,从而使得金融危机期间向上敲出看涨障碍期权的价格系统性的偏高或偏低,这主要取决于波动率和障碍的大小.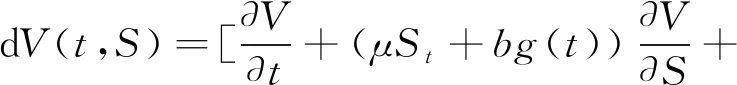
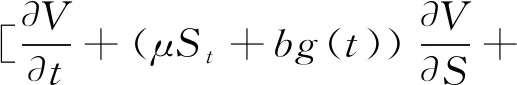
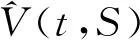
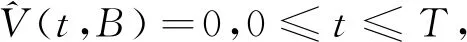
2 Crank-Nicolson差分方法
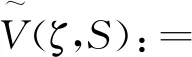
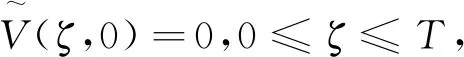
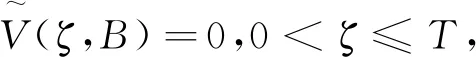
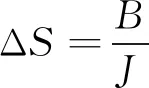
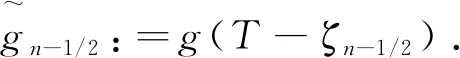
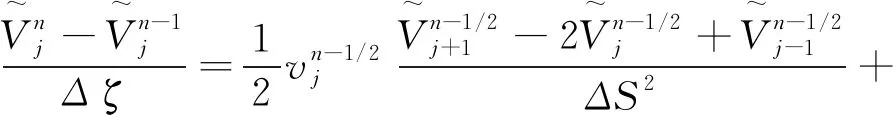
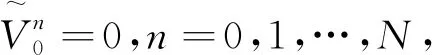
3 数值算例
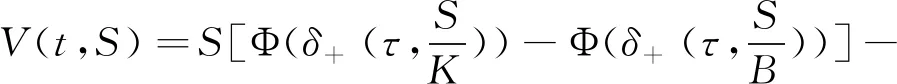
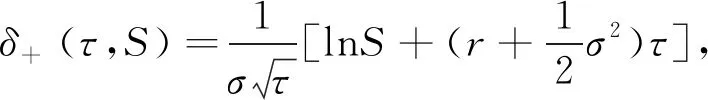
4 结束语

