关于图的符号控制数的下界

尚华辉， 苗连英

(1.永城职业学院 基础部， 河南 永城 476600；2.中国矿业大学 数学学院， 江苏 徐州 221116)

0 引言

图的控制函数是图的控制理论中的一个重要组成部分.图的符号控制函数有着重要的应用背景，因而确定其下界有重要的意义.

为了方便,对于∀v∈V(G),将dG(v)简记为d(v).凡文中未提到的术语见文献[1-4].

在下述定义1的符号控制函数中，f(x)表示顶点x在双值函数f映射下的函数值，记A={v∈V|f(v)=1},B={v∈V|f(v)=-1},f(N[x])表示N[x]中的顶点所对应的函数值的和，f(V)表示顶点集V中的顶点所对应的函数值的和.

定义1[2]设G=(V,E)为一个图，对点集V(G)定义双值函数f：V→{-1,+1},若对于任意的v∈V,均有f(N[v])≥1成立,则称f为图G的一个符号控制函数，并称γs(G)=min{f(V)|f为G的符号控制函数}为图G的符号控制数.

下面给出本文要用到的结论.

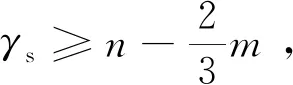
1 主要结果

证明设f为图G的符号控制函数且使得γs(G)=f(V).令A={v∈V|f(v)=1},B={v∈V|f(v)=-1},|A|=t,则|B|=n-t,且γs=|A|-|B|=2t-n.

∀x∈B,且d(x)=3时，由符号控制函数的定义知f(N[x])≥1,则有{y|x的邻点}⊆A,即dG[{x}∪A](x)=3.

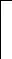
解之得

故有

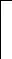
易验证δ≥3时，此下界改进了结论1中的下界.

下面验证定理1中的下界是最好可能的.

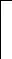
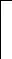
证明设f为图G的符号控制函数且满足γs(G)=f(V).

记|A|=t,则|B|=n-t,γs=|A|-|B|=2t-n.

记m1=|E(G[A])|,则|E(G[B])|=m-m1-|E(A,B)|.

记Ao={x|d(x)=1(mod 2),x∈A},Bo={x|d(x)=1(mod 2),x∈B}.

对于∀x∈A-Ao,有|N(x)∩A|≥|N(x)∩B|,对于∀x∈Ao,有|N(x)∩A|≥|N(x)∩B|+1.

对于∀x∈B-Bo,有|N(x)∩A|≥|N(x)∩B|+2,对于∀x∈Bo,有|N(x)∩A|≥|N(x)∩B|+3.

从而有

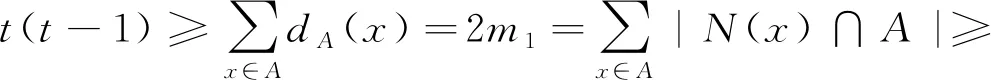
(1)

由式(1)中的不等式2m1≥2{m-m1-|E(A,B)|}+2|B|+|O(G)|得

(2)

由式(1)和式(2)得不等式

(3)

由不等式(3)得

(4)

由式(1)中的t(t-1)≥2m1得

(5)

由式(4)和式(5)得

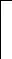
易验证m≥3n时，此下界改进了结论2中的下界.

证明设f为图G的符号控制函数且使得γs(G)=f(V).与定理1中的证明类似，得到

|E(A,B)|≥3(n-t).

(6)

由符号控制函数的定义知顶点x与点集A的邻点数不少于与点集B的邻点数，即∀x∈A,dG[{x}∪A](x)≥dG[{x}∪B](x),故有

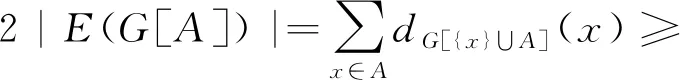
(7)

由式(6)和式(7)得

2|E(G[A])|≥|E(A,B)|≥3(n-t),

(8)

即有

(9)

结合式(8)、式(9)及图的结构知

m≥|E(G[A])|+|E(A,B)|≥

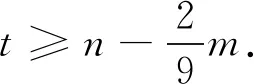
从而有

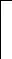
易验证δ≥3时，此下界改进了结论3中的下界.

下面验证定理3中的下界是最好可能的.

2 结论

得到了符号控制数的3个下界，这3个下界分别改进了引言中结论1、结论2、结论3中的结果.此外，还给出了满足上述2个下界的图.