利用“对称美”探究解题思路示例

张 昆， 罗增儒

(1.淮北师范大学 数学科学学院， 安徽 淮北 235000； 2.陕西师范大学 数学与信息学院， 陕西 西安 710061)

在探究数学问题解题思路的教学活动中，启发学生萌生指令操作具体行为活动的“念头”(一种起始性的数学观念)非常重要，除了经验提供的再生性思维[1]具有直觉性提示的“念头”以外，往往还需要创造性思维支持的全新“念头”的出现，才能较好地获得解决问题的思路.那么，这种由创造性思维所萌生的“念头”出自于哪些心理活动过程呢？在探究不等式证明思路的教学设计及其课堂实施中，如何启发学生通过创造性思维萌生指导学生操作行为的合适“念头”呢？这里从“对称美”审美意向的内涵展开教学设计及其课堂实施研究.

1 “对称美”的内涵及其在数学中的体现

提起“对称美”，直觉的理解需要借助于空间图形形象的帮助，但这种直觉并不能很好地达到本质认识.关于“对称美”，其源头出于黑格尔在《美学》中的论述，“美就是理念的感性显现”[2]148.黑格尔在论述抽象形式美时，他将美的要素分类为整齐一律、平衡对称、符合规律与和谐这四种具体形式.他指出，“平衡对称脱胎于整齐一律，并不只是一种抽象地一致的形式，而是结合到同样性质的另一种形式，这另一种形式但就它本身来看，也还是一致的，但是和原来的形式比较起来却存在不一致的因素，由于这种结合，就必然有了一种新的、得到更多定性的，更复杂的一致性和统一性的结果”[2]174.由此认识到，“对称美”是主体审美意向赋予了外在信息内容以四种美的具体形式中的一种形式.

整齐一律是指反映到主体意识结构中的对象信息轮廓中，具有对于某一个环节的重复性与依赖性的特点.例如，当投一枚石子进入一个水面平静的池塘时，石子所引发的圈圈涟漪，就具有这种重复性与依赖性的特点.那些难以出现重复性特点的信息元素中可能存有平衡对称的特点，平衡对称不再像石子投入水面平静的池塘时所引发起的涟漪那样具有不断重复扩展的性态，而是形成了信息元素的某些独立性的特点.平衡对称表现为在某个局部整体中的信息要素满足一定条件的成对出现，这个条件的直观理解在于成对出现的信息要素中的一个信息点构成了另一个信息点的心理“镜像”形式，“对称美”就蕴含于这种理念中.

将黑格尔平衡对称所形成的“对称美”理念应用于数学教学中，许多老师已经做了不少工作.但是，其基础性观念就是借助于信息的这种“镜像”的直观形式.在数学教学设计及其课堂实施领域，一系列的研究成果都只是基于这种“镜像”形式的“对称”，到此便停止了，没有再向前深入一步.

例如，黄美莲[3]指出“教师首先要引导学生正确领悟数学中数字的对称美、图形的对称美、公式的对称美,以及形式和结构的对称美；引导学生学会利用数学本身的对称来为数学问题提供解题条件”.黄老师将关于空间图形直观形式的“对称美”拓展到了数式形式上的“对称美”，增加了数学“对称美”的内容，相应地增强了“对称美”的功效.

唐金波等[4]主要从理论上提出了关于“对称美”审美意向的教学价值，不过，他们也是从数学“对称美”的“镜像”形式出发的，强调了其客观性的一面.其他相关文献也都基本上是从“镜像”形式出发，讨论数学教学中的“对称美”的，这里不再一一罗列.

因此，这些研究成果都没有揭示出“对称美”在数学中所使用的符号形式的信号提示，遑论利用信号提示，启发学生从中萌生探究解决数学问题思路的思维动力.因此，这是本研究的着力点之所在.

由于数学知识的特点主要是通过概念及其表达所使用的符号作为载体，用以刻画空间形式或数量关系的结构，以反映主体的认识及其结果.因此，在写成结论的数学表达中，作为反映客观世界中的空间形式或数量关系的具体符号表达式，所形成的数式结构的这种平衡对称的独立性是非常容易得到体现的.

在数学解题及其教学中，在探究数学问题所提供的外在信息时，解题主体通过选择某些必要的信息元素，组织成信息轮廓，据此轮廓赋予这些信息要素以具体的知识结构意义，与生俱来或通过后天培育发展起来的审美意向(将信息元素按照解题主体所形成的理念塑造信息要素组成轮廓的心理内驱力)起着非常重要的作用[5].因此，主体在处理信息时总是从自己已经掌握了的某种理念出发，希冀把外在信息元素组织成符合审美心理内驱力的轮廓结构，当主体的这种心理内驱力消解完毕时，审美意向的作用也就结束了，有价值的解决问题思路也就应该随之出现了.

在使用分解、排列、组合等结构性手段处理数学问题提供的信息时，由联想或想象补充原始信息的不足之处，解题主体在智囊中所形成的“念头”非常重要，这些“念头”构成了指令解题主体操作信息行为的数学观念，构成了探究数学问题解决思维动力的主导性因素.在真实的思维活动过程中，经验、联想、想象、审美等思想要素都是形成“念头”时思维展开的原始动力[6].由此可知，在探究较为困难的数学问题解题思路时，解题主体的审美意向将直接起着非常重要的作用.

因此，作为形式美的数学结构中的平衡对称性的特点，是经过“人化”了的抽象产物，是运用符号(或图形)语言表示出来的.在这些符号与图形中，存在具有作为审美意向信号的表征性符号，例如，“等号”“不等号”所连接的等式、不等式两边所形成的对称形式，“分数线”所连接的分子分母的对称形式等.这是因为数主要是用符号语言表示客观事物的空间形式与数量关系，因此，符号形式表达的平衡对称所定性的地方，正是客观事物本身所定性的结果，也就是以外在的不能显出主体的生气灌注作用的客观形式为基础，通过表达数学概念与知识的符号将其转化为主体生气灌注的主观形式.当主观形式正确地表达或反映了客观形式时，两种形式的同一[7]且使用合适符号的正确表达就建立起了标准化的数学知识.

因此，在具体的数学知识中，平衡对称的形式要素俯拾皆是，图形结构形式中的平衡要素对称自不必说，数式结构形式中的平衡对称也是非常多的.例如，除了上面所述的等号、不等号与分数线构成形式“对称性”的信号外，还有互为相反数；“函数”与“自变量”的对称形成的“反函数”概念；偶函数定义中的f(-x)=f(x)等，都是“对称美”所具有的信号性体现.这些信号就会提示数学解题主体萌生“对称美”审美意向,形成探究问题思路的心理内驱力.“对称美”审美意向的不断实现过程，就是解题主体心理内驱力的不断释放与消解过程.

2 利用“对称美”审美意向探究不等式证明思路示例

由于学生来自于基因遗传或经受后天训练所萌生与定型了的“对称美”审美意向的作用，当其面临外在数学化信息时，就会立即自觉地利用这种整齐一律、平衡对称、符合规律或和谐等的审美意向作用于这些信息，指导学生选择某些信息要素组织成符合这几种美所定型的形式中的某一种形式.如此将这些信息因素组织成或大或小的轮廓，这就形成了解题主体的心理内驱力，这种心理内驱力转化为探究解决数学问题思路的思维动力，随着信息因素组织得符合解题主体的审美理念的逼真程度一步步深入，这种心理内驱力得以不断地消解与释放，往往解决问题所需要的思路就会出现了[8].这里主要以平衡对称所体现的“对称美”审美意向为例，说明其在探究一类不等式证明思路中的应用.

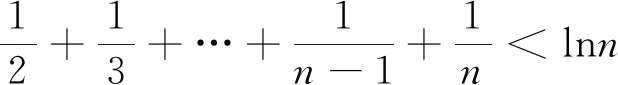
生：……(省略号表示学生的思维暂时中断，下同)

师：大家仔细观察，不等式①具有怎样的特点？

生1：不等式①的左边是一个(n-1)项和的代数式形式，而右边是只有一项的具体代数式的形式.

师：生1准确地把握了不等式①表现形式的具体特点.那么如何利用这种特点，探求证明不等式①的思路呢？

生2：如果通过计算不等式①左边的(n-1)项和，从中得到具体的计算结果，那就只要比较这个结果与lnn的大小就行了.可惜，我不能计算出不等式①左边的一个具体结果.

师：一种好想法.生2的这种想法虽然找不到计算不等式①的左边得到具体结果，但是分析这种想法的来源可能是有价值的.生2的想法是源于不等式①中不等号所连接的两边代数式应该具有同样的特点，不等式①的右边是一项，那么不等式①的左边也应该是一项.这是由不等号连接的两边代数式具有“对称性”特点所决定的.这种“对称性”对于萌生探究解题思路的新想法有帮助吗？

生3：由不等式①中不等号连接的两边代数式具有这种“对称性”形式特点可知，虽然不等式①的左边不能通过具体计算得到一项代数式，但是可否将不等式①右边的lnn写成一个数列的前(n-1)项和的形式呢？如果可以的话，那也就满足了不等号连接的两边具有“对称性”形式特点.

注：在启发学生探究证明不等式①的思路时，数学教师不能将这种以不等号为指示信号的“对称性”直接地奉献给学生，那样，学生就不能萌生“对称美”审美意向的心理源头及其产生的有效作用，不能感受自己在探究思路时启动思维与思维逐步推进过程中的由原始动力及其产生后述每个环节的思维动力的次第展开的心路历程[9].教学设计及其课堂实施活动应该从学生最为原始的“念头”就是计算不等式①左边(n-1)项的和所得到的具体结果，如所知，通过评价与审视求这个(n-1)项的和的心理原因，而揭示出“对称美”的审美意向的心理内驱力,为生3发生这种心理内驱力的“逆向”转移奠定了基础.这是数学教师必须要认识到的并充分认识到的.

师：生3的这种想法可以实现吗？

注：在探究这道题的证明思路时，组织不等式①所提供的外在信息的特点就在于使用“对称美”审美意向，就是说，不等式①所呈现的形式目前不具有“对称美”的特点，而不等号连接的两边代数式应该具有“对称性”的特点，这就萌生了将不具有“对称性”形式特点的代数式转化具有“对称性”形式特点的代数式的“对称美”审美意向，由此而生成了探究解题思路的启动思维与维持思维进展的心理内驱力，这种心理内驱力对于思维的定向、序化都具有非常重要的作用.

与此同时，由于解题主体长期数据、数式计算的经验的浸润，在认知结构中已经形成了“化简”的强烈数学意识，他们在消解关于不等式①的“对称美”审美意向所形成的心理内驱力时，自然而然地就会联想到将不等式①的左边通过具体计算变成一项的结果，从而与不等式①右边的一项形式形成了“对称性”，可惜这种想法不能经由计算达到目的[10].而生3却在这种“对称性”的启发下，想到了把不等式①的右边转化为某个数列的前(n-1)项和的形式，这是可以达到目的的，为生4获得问题解决思路的指令行为的“念头”提供了关键性环节的支点.

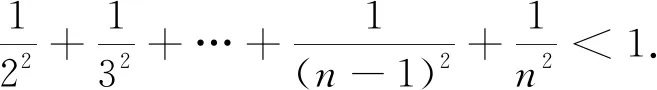
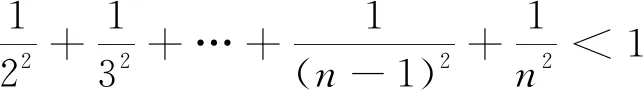
生5：不等式⑦的左边是一个(n-1)项的和的形式，可是不能经由具体计算途径，将其转化为一项的结果.又由于不等号连接的两边具有“对称性”特点，据此希望试探将不等式⑦的右边的这个具体常数1转化为一个数列的前(n-1)项和的形式表达式.如此，设

两式相减，得an=0⑧.

师：怎么办？

生：……

师：需要检视不等式⑦与不等式①所存在的不同点，然后对症下药，从而探究解决问题的思路.对此，大家有什么意见？

生6：我发现不等式①与⑦的左边的值随着n的变化而变化，不等式①右边也应该随着n的变化而变化,而不等式⑦的右边却是不能产生变化的一个常数1，因此出现了⑧式这种结论.这个⑧式对于发现这道题的解题思路没有帮助.我认为，可能正是不等式⑦的左、右边两边代数式的不同形式的性质特点导致了这种方法行不通.

注：不等式⑦的形式不能消解“对称美”审美意向所萌生的心理内驱力，这是因为不等式⑦的左边是一个具有以n为自变量的代数式的形式特点，而其右边却是一个具体的常数1的形式特点，这就会导致解题主体萌生了将不等式⑦的左边通过计算转化为一个常数，或者将其右边常数转化为一个以n为自变量的代数式，这是一种由“对称美”审美意向所萌生的心理内驱力，这种心理内驱力就是探究这道题解题思路的最主要的思维原动力之一.笔者的教学设计及其课堂实施的主要依据，就在于一步一步地启发学生的这种推动思维展开的原动力的实现.

师：生6发现的结论应该很有价值.由于不等式的左边的变量不可能自行消失，所以它就不可能转化为一个常数.那么由于不等号连接的两边代数式的“对称性”特点，不等式⑦的右边这个常数1，能够转化为一个随着n的变化而变化的代数式吗？

注：对于不等式⑨可以看做是不等式⑦的一个“加强不等式”的形式.如所知，这种“加强不等式”概念及其决定了产生解题思路的方法也是具体的实际问题所引起的.这是数学教师在教学设计及其课堂实施中，必须要注意的问题，通过在“真刀实抢”的探究不等式证明思路的过程中，渗透具体的“加强不等式”的数学意识及其形成的具体方法.数学教师可以指出，在生7所使用的这种探究证明不等式⑦的证明思路时，采用的就是一种“加强不等式”的途径，当然，学生尽管没有这样的语言表示，实际上是在执行“加强不等式”的数学观念，它对于某些类型的问题是一种必要的方法.

师：好想法！那么这个X应该是什么样的具体代数式呢？

生8：选择使用

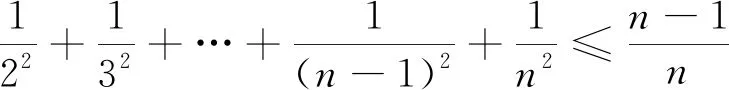
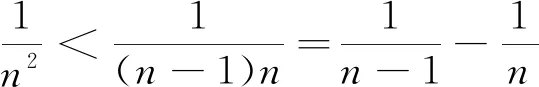
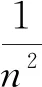
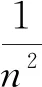
如此，数学教师必须认识到，在自己的教学设计及其课堂实施中，应该通过对教学内容的认真分析，多角度的精心思考，依据其具体特点仔细甄选，利用合适的教学素材(如本文中的例1、例2)，帮助学生揭开这层面纱.如此，竭尽所能地鼓励学生认识到，将这种“求繁”过程转化为与“化简”过程一样地平常，这对于探究一类问题解题思路，具有很好的教学价值[12].

3 结束语

数学解题主体在处理数学问题所提供的数学化信息时，它总是使用已经掌握了的数学概念、数学知识(公式、定理、法则、方法、思想等)作为封装已知信息的范畴性框架，由这个范畴性框架赋予外在信息以意义，从中获得数学问题解决的思路.在选择使用某个范畴性框架赋予外在数学化信息以意义时，对于一类问题，“对称美”审美意向所萌生的心理内驱力，形成了探究解题思路的初始的维持与不断展开的思维动力.