基于K-Means聚类和改进多分类相关向量机的台区线损计算方法

谢 林 李红伟 袁 岳 周海林

(1.西南石油大学电气信息学院 成都 610500；2.国网四川省电力公司资阳市雁江供电分公司 资阳 641300；3.四川大学电气工程学院 成都 610065)

1 引言

低压配电系统的线损管理是电力系统线损管理的重要组成部分，涉及配电系统的规划、运行、营销和计量。统计的线损包含管理线损，但由于低压配电系统网络结构复杂、用户数量多、性质复杂、海量数据管理困难等原因，低压配电系统线损计算存在较大偏差[1]。理论线损的计算是基于电网设备参数、操作数据和功率流以及载荷分布理论，它可以准确地了解电网损耗的构成，并且提供一个可靠的依据充分利用电网企业的潜在损失。

配电网处于发电、输电、配电的末端，其设备数量多、覆盖范围广、电压等级低，导致配电网损耗大。到目前为止，低压配电系统的线损仅根据用户文件进行简单计算，未考虑负荷、供电半径的影响。此外，目前的计算周期一般都是按日计算，当运行方式发生变化时，无法进行实时线损计算[2]。随着分布式可再生能源的广泛集成，低压配电系统中的潮流、线损、电压分布发生了变化，对低压配电系统的线损管理产生了很大的影响。

配电网理论线损计算方法主要有前向-后向扫描法、等效电阻法(容量法和电学法)、均方根电流法、平均电流法、最大电流法等[3]。这些算法以前受配电网自动化程度的限制，在使用时存在不同的局限性，如计算工作量大，没有考虑负荷曲线变化的差异、各负荷节点的实际功率、节点电压、线路电抗等[4]。近年来，人工智能算法的发展逐渐应用于线损率计算，比如利用神经网络搭建计算模型，通过大量的样本训练，拟合特征参数和线损之间的关系。文献[5]引入多源数据，并通过随机森林法搭建线损计算模型，在一定程度上提高了线损计算效率；文献[6]通过建立线性回归模型进行数据挖掘来预测线损率，得到较好的准确率；文献[7]通过聚类算法来确定神经网络的隐层节点，来构建线损计算模型，具有较快的计算速度。

为此，本文提出了一种基于K-Means 聚类算法和多分类相关向量机(Multi classification correlation vector machine，MRVM)的线损快速计算方法。首先选取与配电网线损有关的电气指标作为模型的输入；针对指标接近，但网架结构和负载特性会影响线损率的情况，本文采用K-Means聚类算法对台区进行聚类分析，简化数据处理，对每一类台区进行具体分析；然后搭建果蝇算法优化MRVM 的模型，计算台区线损。以四川资阳供电公司为例，对配电网理论进行了理论在线损耗计算，并与传统理论线损计算结果和综合电力线损管理系统进行了对比，验证了该方法的有效性。

2 模型输入特征参量选取

为了改善多分类相关向量机的性能，需要优化输入参数，减少维度。通过现场经验和相关电力系统理论知识得知影响台区线损率的参数有供电半径、线路长度、负载率、用电性质、三项不平衡度、电压等，考虑参数的影响大小及获取难易程度，选取与低压台区线损率密切相关的4 个电气参数作为输入。通过反复筛选，选取了供电半径、线路总长、负载率以及用电种类及用电种类占比情况[8]，由于研究的是低压台区线损，因此选用居民用电性质来表示用电性质。

(1) 供电半径X1(m)。供电半径指的是最远的用户到电源点的线路长度，一般用于控制线路电压降，是判断供电半径是否正确的重要参数。

(2) 低压线路长度X2(m)。低压线路长度指的是所有低压台区线路总长。

(3) 负载率X3(%)。负载率表示该变压器实际承担的负荷与额定容量之比，用于反映变压器的承载能力。

(4) 用电性质比例X4(%)。用电性质比例表示负荷用电性质与供电量的比例，能够反映所在台区的用电性质。

选取上述4 种参数作为MRVM 的输入，由于4中变量的量纲不同，对其进行标准化处理，处理方法如式(1)～(3)所示

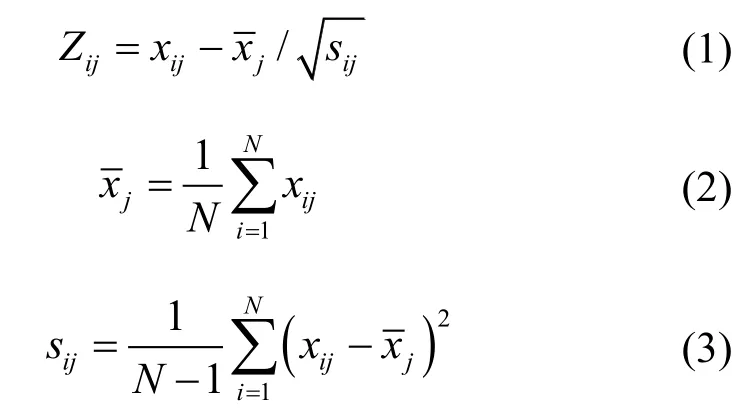
式中，Zij表示标准量；表示xij的均值；sij表示xij的方差。

3 基于系统聚类和果蝇优化MRVM的低压台区线损计算

3.1 K-Means 聚类算法

为了减少网架结构带来的计算误差，需要对台区样本进行聚类分析。在对其进行聚类前，首先要计算样本之间的相似度，一般用距离来表示相似度。本文采用K-Means 聚类算法来对台区进行聚类分析，该算法以距离作为相似性的评价指标，以误差平方和准则函数作为聚类准则函数，是一种迭代求解的聚类分析算法，该算法步骤如下[9]所示。

(1) 初始化：随机选取K个点，作为聚类中心。

(2) 类划分：按照式(4)计算每个点到K个聚类中心的距离，然后将该点分到最近的聚类中心，这样就形成了K个簇。

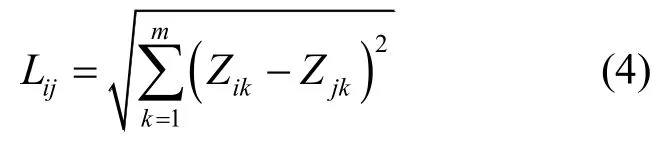
(3) 中心点计算：再重新计算每个簇的质心(均值)，以此作为聚类中心。

(4) 迭代计算：重复以上步骤(2)～(4)，直到质心的位置不再发生变化或者达到设定的迭代次数，用式(5)判断是否收敛。

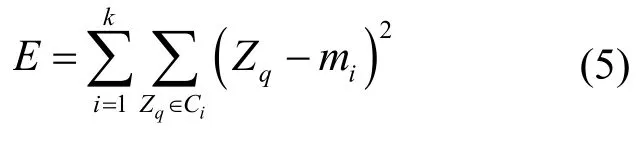
式中，mi表示Ci的中心簇；Zq表示其样本。不断进行迭代计算，直到E值收敛。

K-Means 聚类算法主要有如下缺点。

(1)K值需要预先给定，然而K值是很难估计的，并且对噪音和异常点十分敏感。

(2) K-Means 算法对初始给定的质心十分敏感，选取不同的中心点，会得到不同的聚类结果。

(3) 该算法有可能陷入局部最优。

为了解决以上问题，本文通过聚类结果的轮廓系数St确定K的大小，轮廓系数的计算方法如式(6)所示[10]

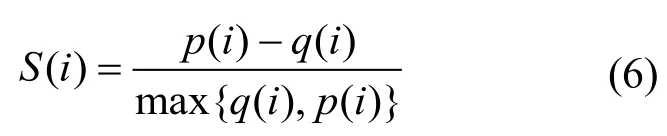
式中，q(i)表示点i到所在类别其他点的平均距离；p(i)表示该点到非所在类别中其他点的距离最小值。计算S(i) 的均值作为St，St越大，表示聚类效果越好，即

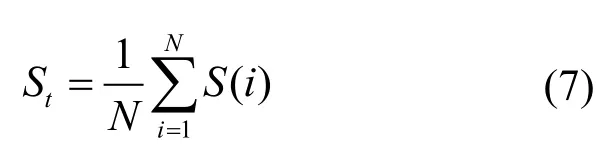
为了解决局部收敛问题，可以多次随机选取聚类中心，最后比较各自完成后的畸变函数值，畸变函数越小，则说明聚类效果更优[11]。

本文选取低压台区供电半径，低压线路总长，负载率以及用电比例最小值作为电气指标值，台区评价指标如式(8)所示[12]

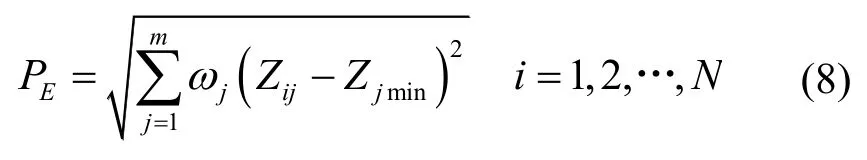
可以看出，参数PE可以反映线损，并且变化趋势相同，因此，可根据PE的值将样本分为k组，让每组的中心作为初始聚类中心。

3.2 多分类相关向量机

多分类相关向量机(MRVM)是在相关向量机(RVM)的基础上进行了扩展，该算法相关向量数量少，泛化能力强，可解决小样本、非线性问题。MRVM使用分层贝叶斯模型，能以概率形式给出结果，便于分析问题的不确定性[13]。

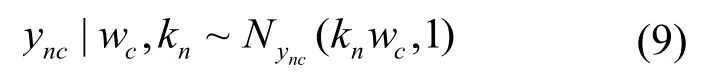
式中，ync表示矩阵Y的n行c列；w表示矩阵Wc的第c列；N x(m,v) 表示变量x服从正态分布。设多项概率联系函数t n=i,yn＞y nj∀j≠i，则多项概率似然函数公式为[14]

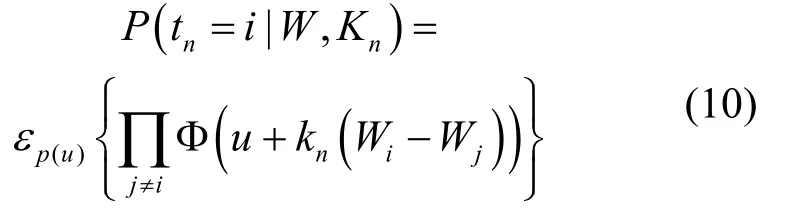
式中，u服从均值为0，方差为1 的正态分布，为了提高模型的稀疏性，使αnc服从超参数分别为a，b的Gamma 分布[15]。MRVM 采用分层贝叶斯模型结构，由上述可知其模型结构如图1 所示。

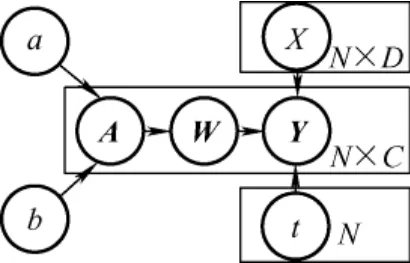
图1 分层贝叶斯模型

由此模型图可得出后验概率为

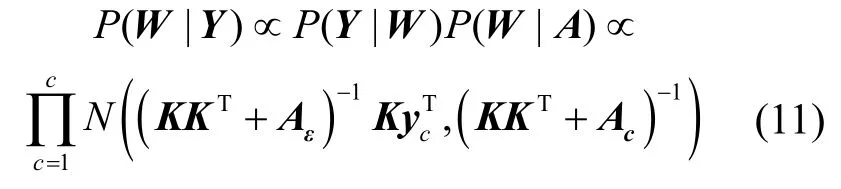
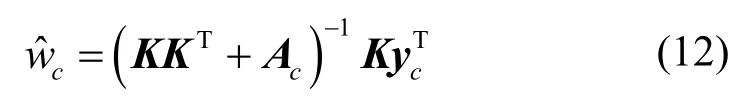
权重向量的先验值的后概率为

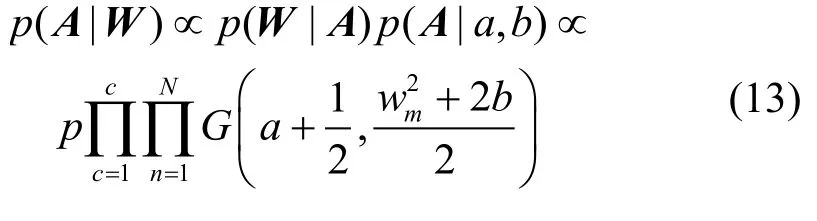
3.3 果蝇算法优化的多分类相关向量机

果蝇算法被广泛用于机器学习的参数优化，大大提高了机器学习的效率[16]。其中，种群大小取10，复杂的取20～50；搜索半径为一正整数，搜索方向为0～1 之间的随机数；迭代次数要根据计算结果，一般迭代次数越多，结果越精准，但太多会导致效率低下。

3.3.1 果蝇算法优化步骤

果蝇算法的7 个步骤如下所示。

(1) 对果蝇个体初始化，即赋予初始位置。

(2) 设置搜索方向和搜索半径。

(3) 计算每个果蝇到原点长度和味道浓度的判定数值。

(4) 将浓度判定值代入适应函数中，计算果蝇位置和味道浓度值。

(5) 比较味道浓度值，寻求最优味道浓度值。

(6) 把步骤(5)的最优值记录下来，所有果蝇朝这个方向飞去。

(7) 重复步骤(2)～(5)，直到迭代收敛。具体算法流程图如图2 所示。

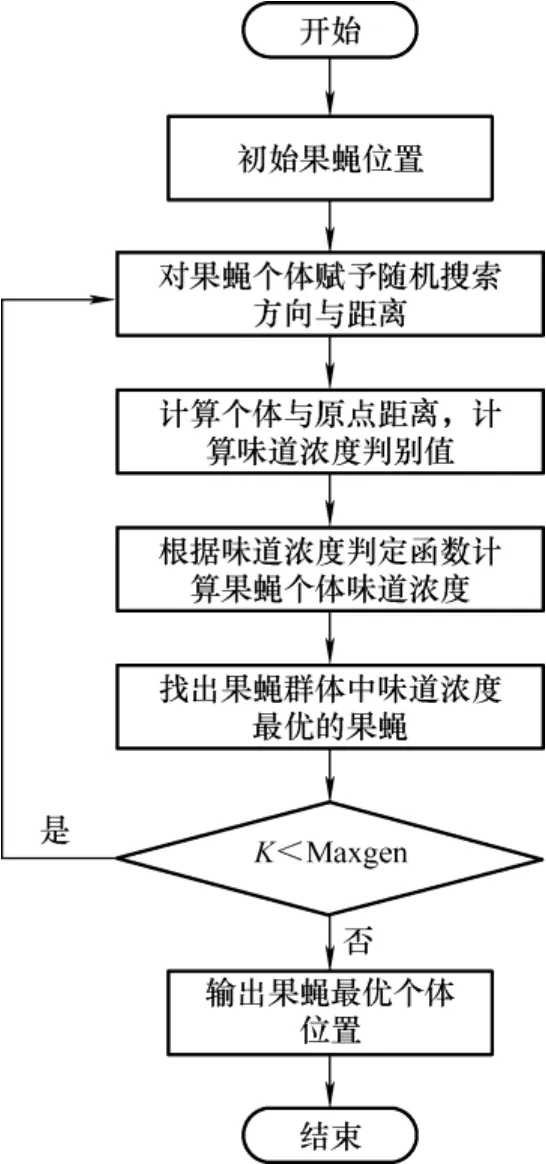
图2 果蝇算法流程图

3.3.2 果蝇算法优化MRVM 参数设计

MRVM 核函数参数的选择对模型具有较大影响，包括惩罚参数、径向基核函数参数和敏感因子。仅人为经验选择参数不能达到理想效果，达不到精度要求，因此，本文选择果蝇算法进行寻优，流程图如图3 所示。

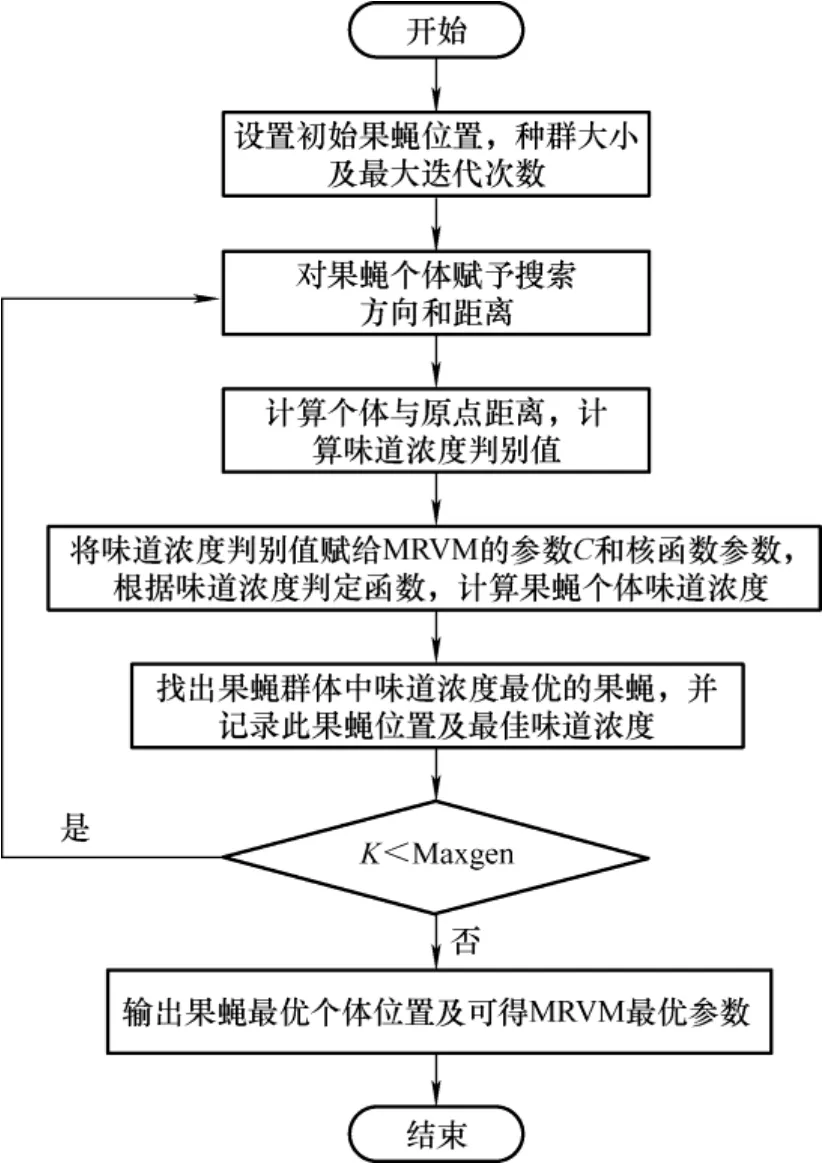
图3 果蝇算法优化MRVM 流程图

3.4 台区线损计算

3.4.1 台区线损归一化处理

由于变压器台区线损的指标量纲不同，因此需要对其进行归一化处理，选取台区线损率作为MRVM 的输出，其输出值域为(0，1)，因此需要将线损率归一化在(0，1)区间内。本文采用式(14)进行归一化处理[17]

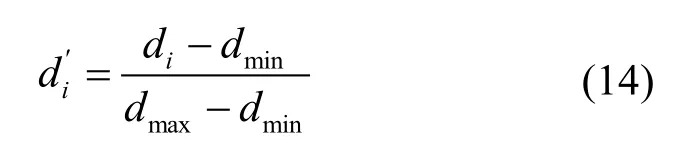
式中，di为归一化前的值；di为归一化后的值；dmax和dmin分别为样本最大值及最小值。

3.4.2 结合K-Means 和MRVM 的线损计算步骤分析

结合 K-Means 聚类算法和果蝇算法优化MRVM 模型计算低压台区线损率分为4 个步骤，具体如下。

(1) 选取台区线损的电气特征参数指标，并对其标准化处理。

(2) 利用K-Means 聚类算法将台区样本进行聚类处理。

(3) 利用果蝇算法优化的MRVM 模型计算台区线损率。

(4) 对计算结果进行误差分析。

本文采用均方误差Em来衡量计算结果的整体误差，假设台区样本数为N，计算公式如下[18]

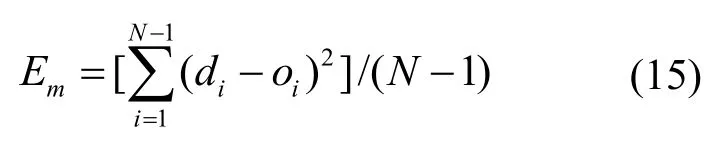
除整体误差外，还需要考虑单个样本误差情况即相对误差，计算方法如下[19]所示

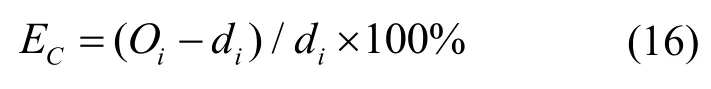
计算流程图如图4 所示。

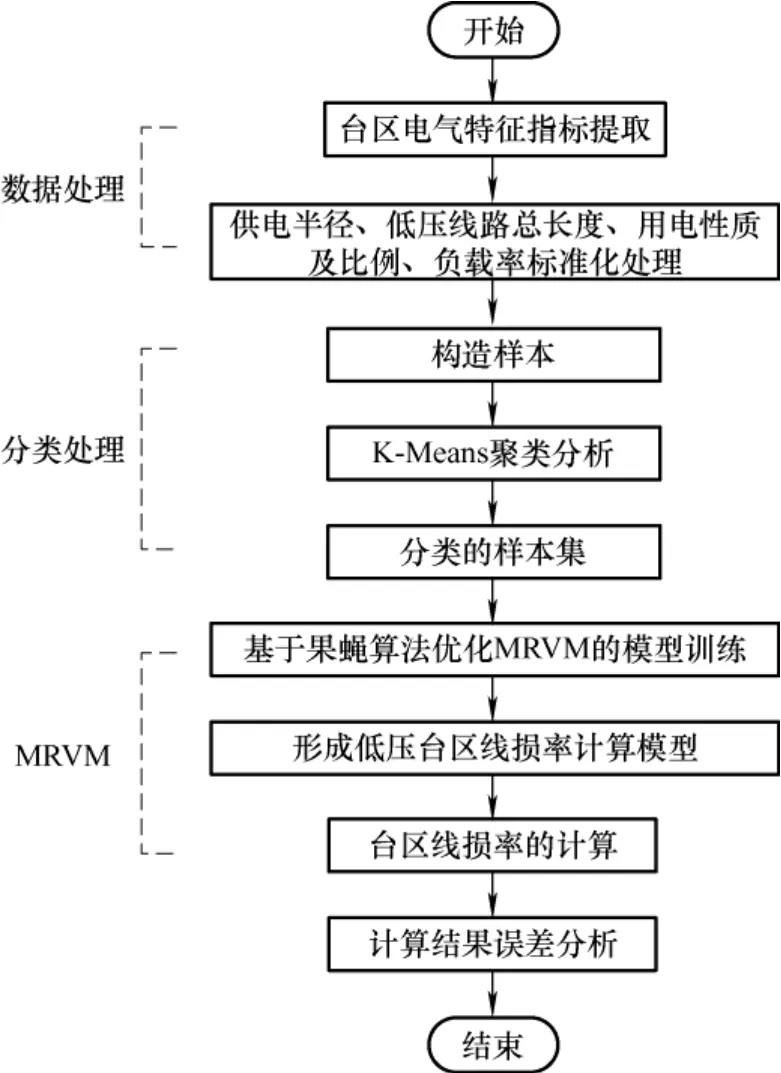
图4 台区线损率计算流程图

4 实例分析

4.1 低压台区样本分类

为了验证该模型计算的实用性，一共选取了600 个样本，按照第2 节所述，选取台区4 个指标作为输入，分别为：x1为居民用电比例，x2为供电半径，x3为低压线路长度，以及x4为负载率，输出为线损率d(%)。

使用上述600 样本进行聚类分析，然后根据标准化后的数据计算样本的性能指标PE，然后根据性能指标的大小进行排序[20]。通过聚类分析发现，当聚类数目k等于6 时，聚类结果的轮廓系数达到最大值，因此本文把k值设为6。根据PE值把样本分为 6 类，则样本的聚类中心如表 1所示。

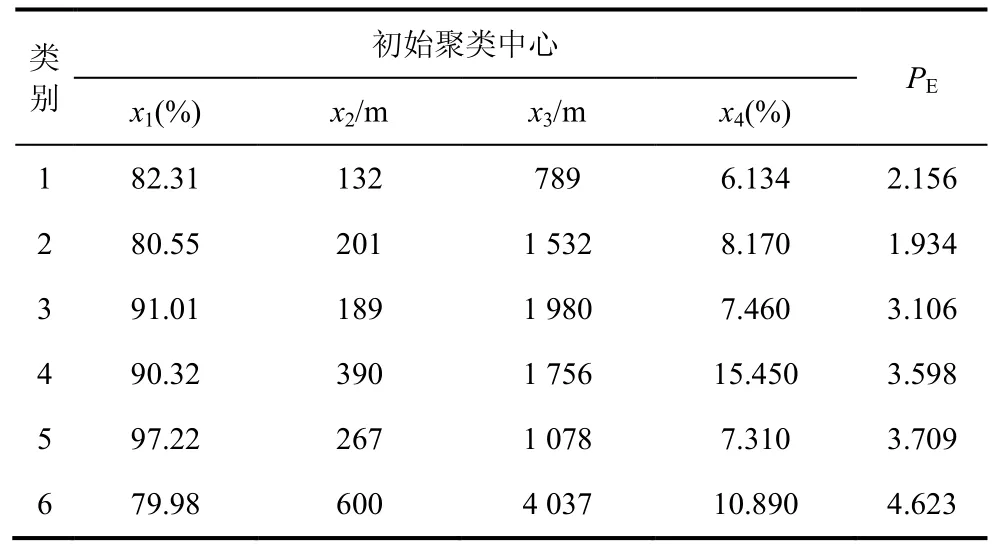
表1 样本聚类中心

低压台区样本聚类结果如表2 所示。由表2 可知，6 个类别所含样本数分别为150、301、11、40、85 和13，总共600 个样本。

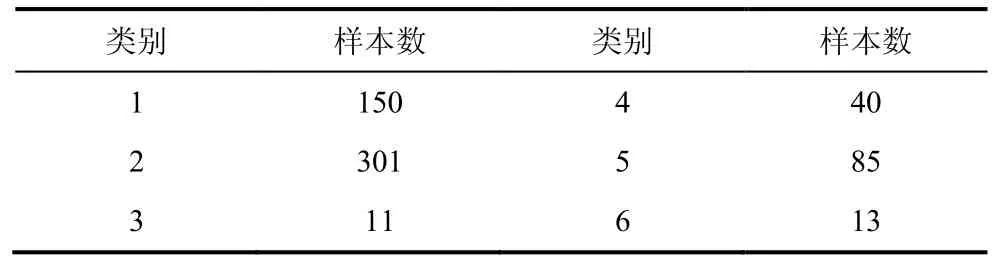
表2 各类别所含样本数

4.2 低压台去线损率计算及误差分析

使用上述6 类样本分别训练果蝇算法优化多分类相关向量机(MRVM)模型，在训练时，设置目标误差分别为：0.01、0.005、0.001、0.000 1，得到线损率结果如表3 所示。

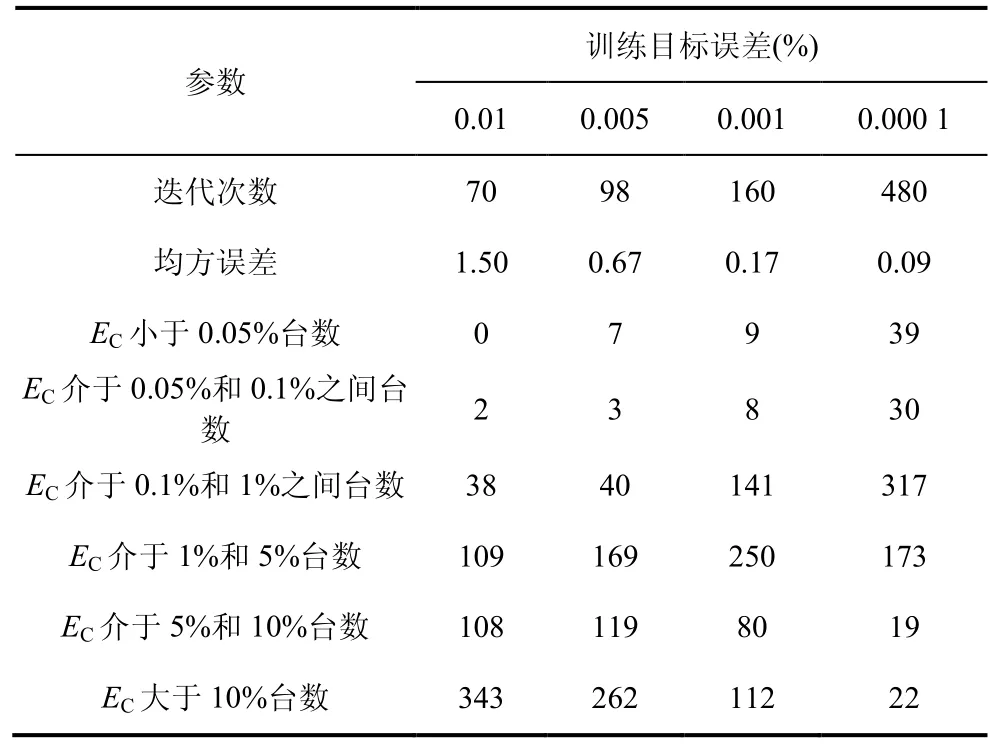
表3 不同训练目标误差下的线损结果分析

由表3 可知，训练目标误差越小，模型计算结果越准确，但迭代次数增多，同时有可能出现不收敛的情况。果蝇算法优化MRVM 模型在训练目标误差为0.000 1 时仍然能够实现全局收敛，线损率EC结果非常小，迭代次数达到480 次，时间消耗为6 s，时间消耗仍在可接受范围内。

设置训练目标误差为0.000 1，得到实际线损率和估计线损率，6 类样本计算结果如图5～10 所示。

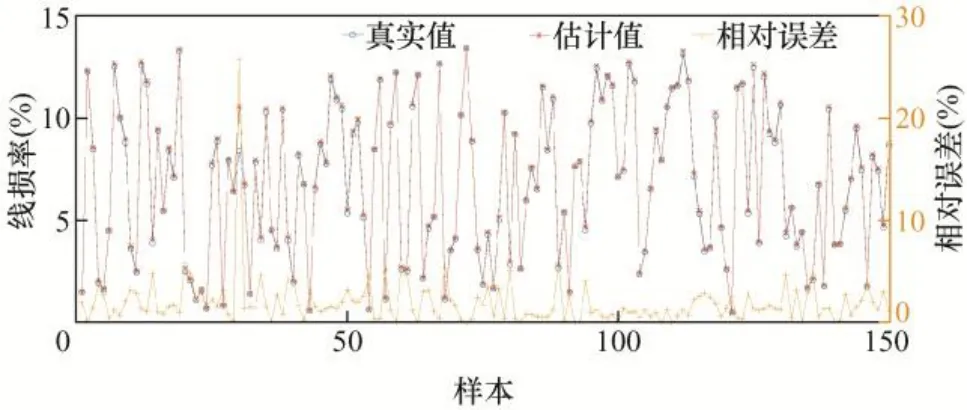
图5 第1 类样本误差结果

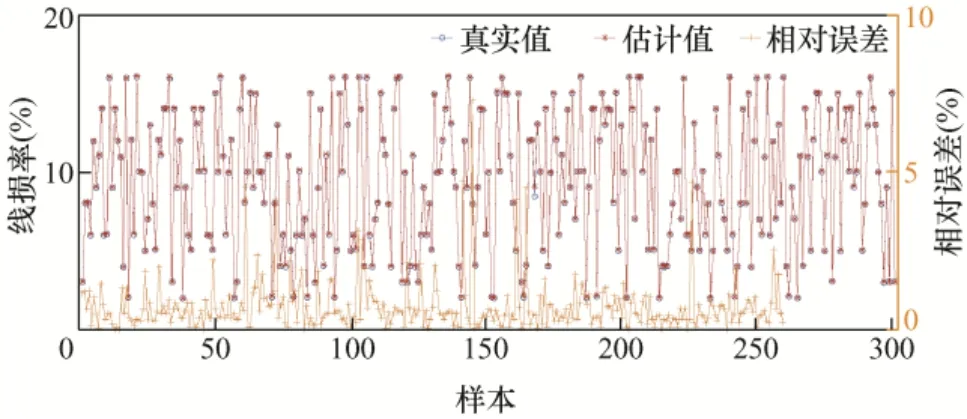
图6 第2 类样本误差结果

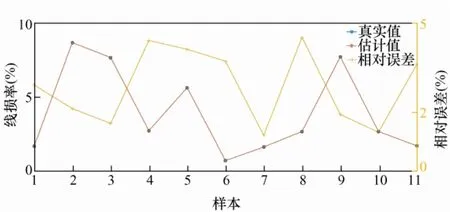
图7 第3 类样本误差结果

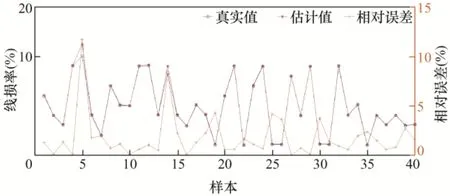
图8 第4 类样本误差结果

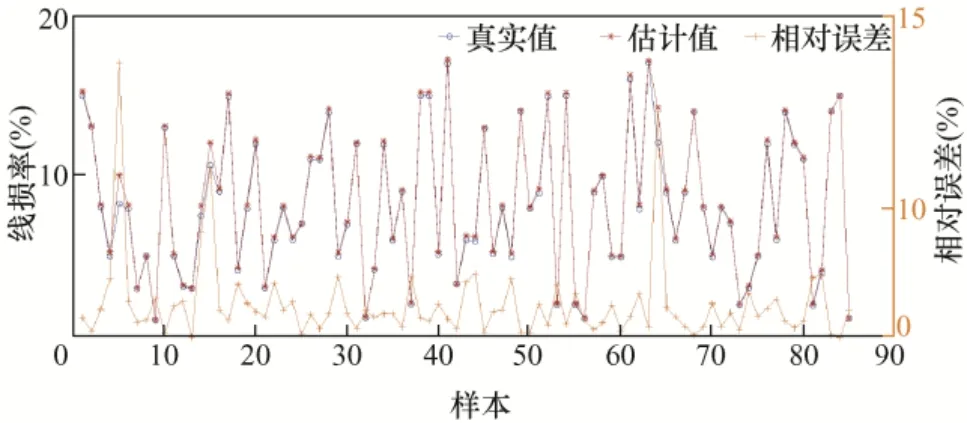
图9 第5 类样本误差结果

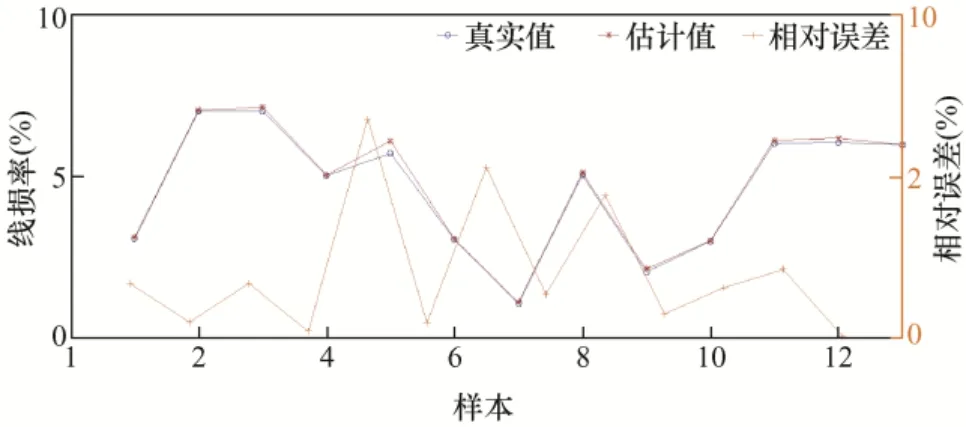
图10 第6 类样本误差结果

以上为6 类样本的误差结果分析，从图5 中可看出第1 类样本中的样本30 的误差率达到了25.7%；第2 类样本的误差率都在10%以下，误差率最高的样本168，误差率也才7.3%；第3 类样本误差率在0.5%以内，误差非常小；第4 类样本误差率最大的为样本5，达到了11.7%，样本14 误差率为8.2%，其他样本误差率都小于5%；第5 类样本的样本5 误差率达到了21.4%，样本15 和样本64误差率分别为13.2%和17.6%，其余样本误差率均在10%以下；第6 类样本中，样本5 误差率最高为6.8%，样本7 次之，误差率为5.3%。下面对误差率在10%以上的样本校核。

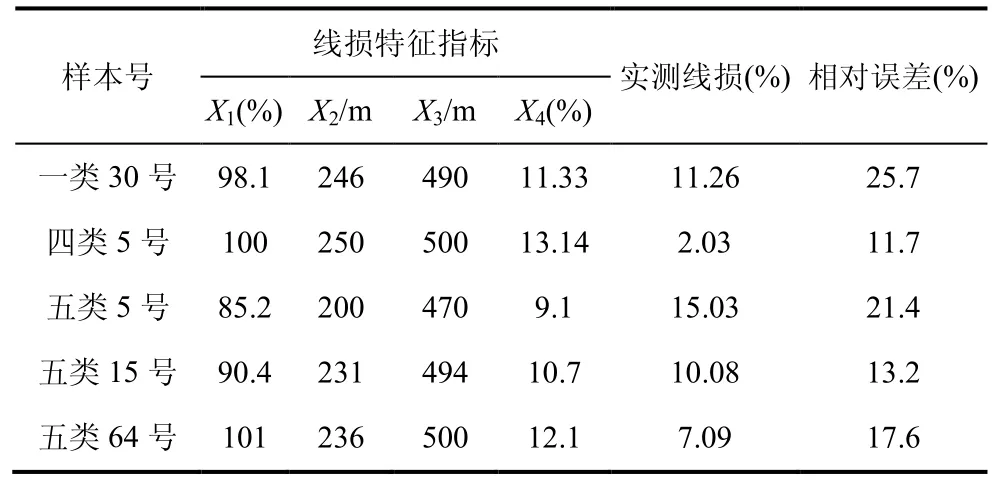
表4 误差率10%以上样本校核

根据电力系统相关理论，特征指标值越大，则线损率越大，然而对比第五类样本的5 号、15 号和64 号，5 号样本的X1、X2、X3、X4均小于15 号和64 号对应的指标值，然而其实测线损率最大，因此可判断5 号实测值不准确，需要重新校核；同理可对比第五类样本的15 号和64 号，15 号样本线损率理应小于64 号样本线损率，然而实测线损值得到相反结果，因此可推测15 号和64 号的实测值存在问题。依此对比一类样本的30 号和四类样本的5 号，需要重新校核实际测量的线损值，然后和模型的预测值作对比。通过校核后，得到这5 个台区样本的线损率为 11.31%、11.22%、10.14%、12.17%、14.28%，重新计算相对误差率，得知误差率都下降到了5%以下。

4.3 果蝇算法优化MRVM 模型和标准MRVM 结果比较

为了验证基于果蝇算法优化MRVM 模型的优越性，设置目标误差为0.01，把计算结果进行比较，结果如表5 所示。

表5 标准MRVM 模型与果蝇算法优化MRVM 模型计算结果比较

通过表5 可看出，果蝇算法优化的MRVM 跌得次数更少，且有更高的线损计算准确率。

5 结论

本文提出了一种新的低压台区线损率计算方法，把该计算方法应用于资阳低压台区线损计算，得到如下结果。

(1) 通过K-Means 聚类算法对台区样本进行聚类分析，可解决以为台区样本分散导致的计算误差较大的问题。

(2) 在台区分类后，搭建果蝇算法优化的M-RVM 线损率计算模型，并对其进行训练，得到线损率计算结果

(3) 对资阳地区的600 个台区样本进行实例验证，通过计算证明了该算法具有较快的收敛速度和准确率。