基于多维特征和GBDT模型的输电线路线损率预测

余佶成 周 峰 王江储 谢从珍* 岳长喜 朱 凯 杨建华

1(中国电力科学研究院有限公司 湖北 武汉 430074) 2(华南理工大学电力学院 广东 广州 510641) 3(国家电网公司华中分部 湖北 武汉 430077)

0 引 言

线损率综合反映了电网的规划、生产和管理水平，是考核电力部门的重要标准[1]。然而理论线损率计算的误差会导致报表不准，难以反映实际线损情况，给线损管理带来极大障碍。随着线损精细化管理工作的推进，亟需精准的线损率计算方法。

目前理论线损率计算方法[2-4]主要应用电流法，包括最大负荷损耗时间法、损失因数法、代表日均方根电流法、电量法、负荷曲线特征系数法、等值电阻法、电压损失法和改进潮流法等。但由于输电线路的运行方式、杆塔参数及位置都不同，仅考虑电流、电压等参数的理论线损率计算方法对于不同线路的泛用性有待研究。

近年来，随着智能电网的不断发展，理论线损率计算方法对元件参数、运行数据的精细化要求使其不再适应智能电网下线损率计算快速性、泛用性的特点，基于统计分析、机器学习的新方法，例如回归分析、神经网络、支持向量机等开始受到关注，并得到了一些应用。

文献[5]基于改进极限学习机算法构建线损计算模型，通过蚁群算法对极限学习机模型进行优化构建多维参量数据与线损的拟合模型，但该方法没有克服蚁群算法可能造成的局部性问题。文献[6]考虑到不同线路网架结构之间的关联知识，采用聚类算法对线路进行分类提取线路类别特征，并根据类别的不同分别构建神经网络模型，但经过聚类后单个聚类模型训练数据的数量减少，得到的模型泛化性降低。文献[7]通过层次分析算法选取部分强关联因素，采用多灰色模型拟合关联因素与线损率的关系，但层次分析法为主观赋权的数据融合方式，难免存在一定的主观局限性。以上方法通过分析供电量、线路长度等理论线损率计算参量对线损率的影响构建了回归模型，但缺少对于历史线损率、电压等时序数据趋势变化以及杆塔信息等多维信息的深度挖掘，模型学习的数据知识不完备，模型计算精度存在提升空间。

针对目前线损率计算方法存在的问题，本文提出一种基于多维特征和GBDT模型的输电线路线损率预测方法。针对线损率计算中存在的线损率信息、电压电流等时序信息及线路本体信息，通过特征工程构建能够细致描述线路状态的多维特征；然后通过GBDT模型拟合特征与线损率的关联关系，建立输电线路线损率预测模型，最后利用某省500 kV输电线路实际数据验证该方法的有效性。

1 数据来源

本文采用数据为某省31条500 kV以上输电线路的实际线损相关信息，主要包括电能计量数据、气象数据、潮流数据及线路本体数据四类。其中电能计量数据包括数据采集日期、供电量和线损等电能表计量关联数据；气象数据包括始末电站的小时内降水量、温湿度、风速风向和气压数据；潮流数据包括母线端的电压、电流、有功功率和无功功率数据；线路本体数据包括投运时间、电压等级、线路总长度、杆塔呼称高、杆塔档距以及杆塔相序等。数据采集日期为2017年9月—2019年4月，总计10 200条数据。部分数据样本如图1所示。

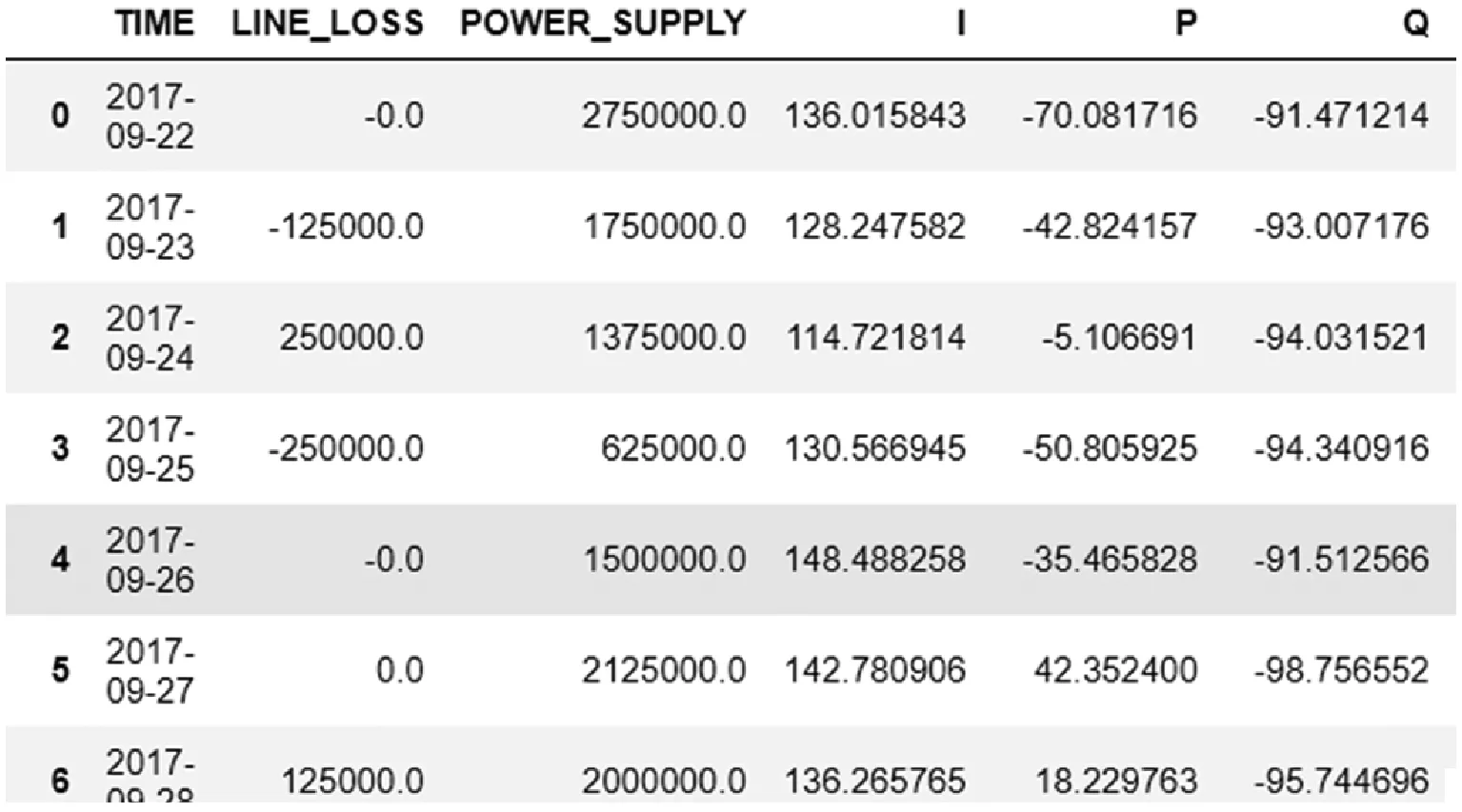
图1 数据样例

线路数据按式(1)计算线损率并用以替换线损数据，得到原始数据。

(1)

2 基于多维信息特征工程的输电线路线损率计算理论

2.1 考虑线损率信息的EWMA特征构建

指数加权移动平均(Exponential Weighted Moving Average,EWMA)方法[8]通常用于计算中短期时间序列的发展趋势，其在考虑高权重的近期数据的同时，通过逐渐减小数据的权重，补充远期数据反映的整体性趋势。

考虑线损率信息的EWMA特征构建流程如下：

对于某条线路的日线损率序列L=[l0,l1,…,ln]，n为线损率序列样本数，第i天线损率的EWMA特征ei由式(2)计算。

(2)

式中：α为平滑参数，α取值范围为(0,1]。采用差分进化法[9]最小化目标函数以得到最优α值，目标函数θ计算如下：

(3)

由式(2)可知，若日线损率序列按日期顺序排序，第n+1天后的EWMA特征将不变，难以描述3天以后的线损率情况。

考虑到线损率与供电量峰谷的时间分布的相关性，将线损率序列数据按星期情况拆分为星期一、星期二、星期三、星期四、星期五与周末六类，每类数据按式(2)计算，得到六类EWMA特征，再次按日期顺序拼接六类EWMA特征，得到变化的计算日后7天内的EWMA特征[en+1,en+2…,en+7]。

2.2 时序信息的统计量特征构建

气象、电压和电流等信息为时序数据，挖掘时序数据在一定时窗内的统计量特征能够细化描述当时线路的实际线损情况。

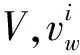
(4)

(5)

每类影响量拓展为4类统计量特征，图2为电流拓展的统计量特征。

图2 统计量特征样例

2.3 线路本体信息的线路特征构建

线路本体信息是多类异构数据的集合，其中线路信息如电压等级、投运时间等为固定参数，能够直接作为线路特征描述线路状况，而线路杆塔信息则存在数值型信息如呼称高、档距等，以及类别型信息如相序、杆塔地形地质等，且线路中每基杆塔的信息不完全一样，无法直接作为线路特征。

对于数字型信息，提取平均值作为线路特征，例如线路呼称高特征为线路内所有基杆塔呼称高的平均值。

对于类别型信息，采用独热编码[10]构造线路特征。独热编码采用不同位的状态寄存器来对多个状态进行编码，任意时刻只有一位有效。对于类别型信息K，K存在NK个状态，K参数处于l状态的第i条线路的第j基杆塔在经过独热编码后得到序列Kij如下：

(6)

将线路每条杆塔的状态位对应加和，得到线路特征Ki，如式(7)所示，其中Ntower为线路杆塔数。

(7)

例如，相序信息总计包含“ABC”“BCA”“CAB”“ACB”“BAC”和“CAB”总计6类状态，则对于有4基杆塔的线路的相序线路特征如表1所示。

表1 4基杆塔线路的相序线路特征构建

2.4 GBDT模型

由于上文中构建的多维特征不仅有电压、电流等数值型数据，也存在如杆塔类型、相序等类别型数据。本文采用能够灵活处理各种类型数据的GBDT模型作为机器学习拟合模型，GBDT模型[11]是一种融合多个树模型计算结果，不断减少模型在训练过程中产生的残差以实现数据的分类或回归的集成模型。相比于依赖数值型数据，优化高维特征空间距离的常见机器学习算法，GBDT模型每次对一个特征进行划分，对于类别型数据也有很好的拟合效果。

对于给定线损率预测数据D=[ZT,yT]，N为样本数量，Z=[Z1,Z2，…,Zi,…，ZN]为输入的多维信息特征，i=1,2，…，N，y=[y1,y2,…，yN]为输出线损率值。GBDT预测模型的构建流程如下：

(1) 初始化模型。估计使损失函数L(yi,γ)最小的模型参数γ，将其作为初始模型f0(Zi)，即:

(8)

(2) 设T为迭代次数，对于第t次迭代，t=1,2,…，T，执行以下步骤①-步骤④。

① 按下式计算当前模型损失函数与模型的负梯度rit，即残差:

(9)

② 将rit作为样本Zi新的标签，得到新的样本数据集[(Zi,rit),i=1,2,…，N]，将其作为新的训练数据，拟合得到下一棵回归树模型，新的树模型由叶子节点Rjt(j=1,2,…，J)组成。J为回归树模型的叶子节点数。

③ 对每个叶子节点Rjt，计算样本的最佳拟合值γjt。

(10)

④ 更新第t次迭代的模型：

(11)

式中:I(Zi∈Rjt)为指示函数，当样本Zi属于叶子节点Rjt时，该函数值为1，否则为0。

(3) 输出最终模型fT(Zi)。

(12)

如图3所示，通过T棵树的迭代、组合，得到最终的GBDT回归模型。

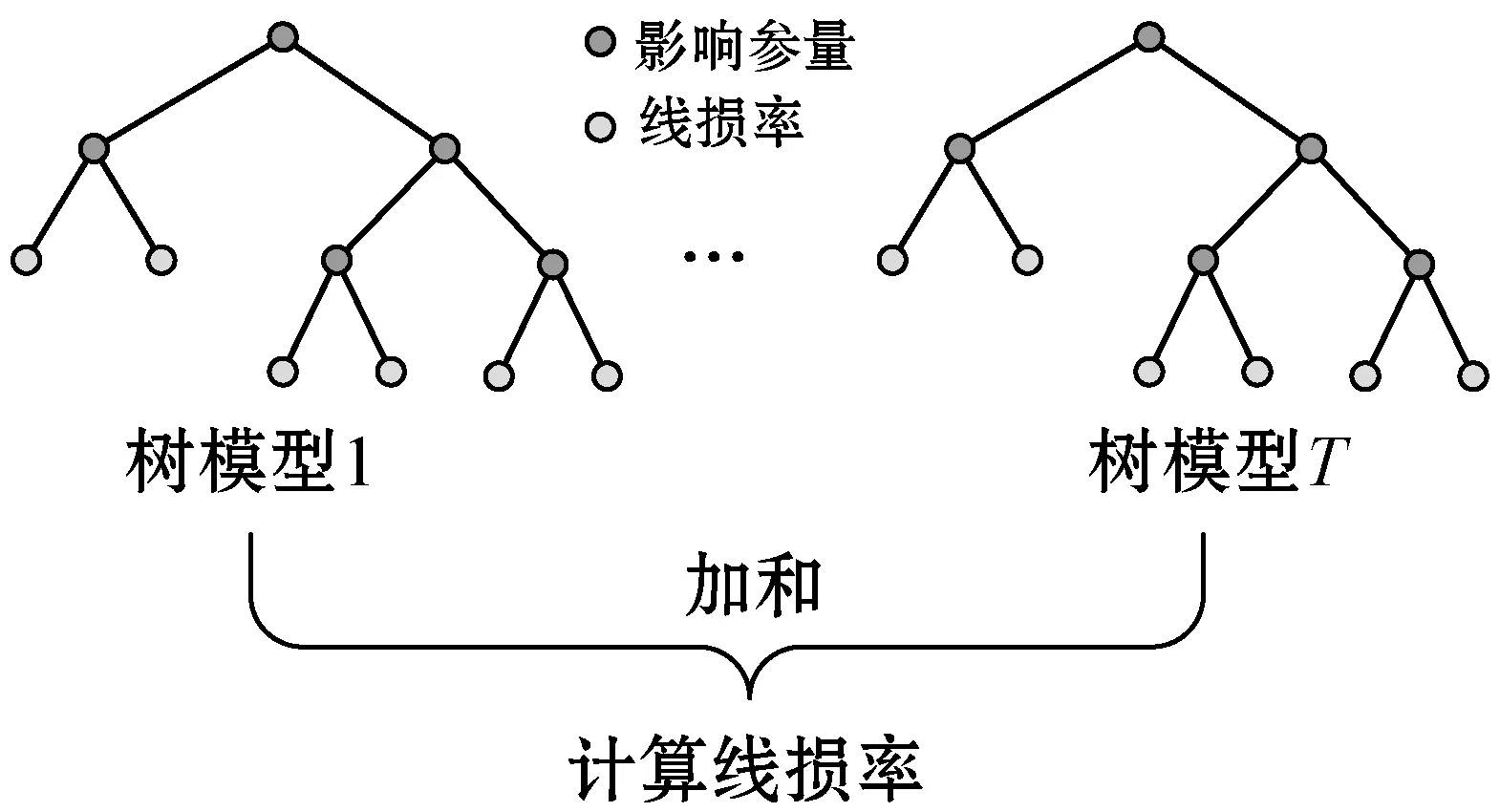
图3 GBDT模型示意图

3 输电线路线损预测模型建模流程

基于多维特征和GBDT模型的输电线路线损率预测模型建模流程如图4所示。

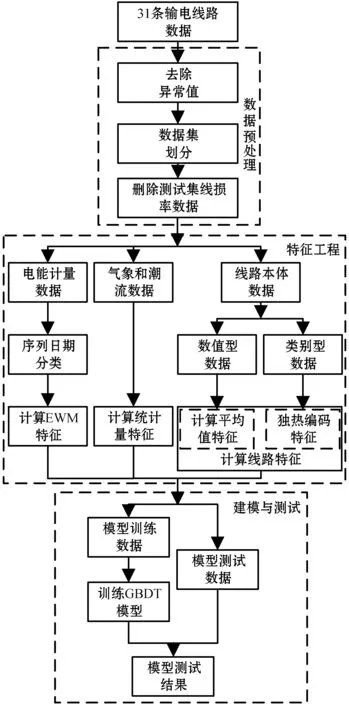
图4 输电线路线损率预测建模流程

3.1 数据预处理

数据预处理首先对31条输电线路原始数据去除异常值。根据线损理论，设置线损率在[-10%,10%]为正常值。去除异常值后对数据集划分训练集及测试集，对每条线路数据按时间提取2019年3月后的数据作为测试集，剩余为训练集，训练集总计9 434条，测试集总计677条。记录测试集的线损率数据作为模型验证依据，将其统一赋值为0用于测试。

3.2 特征工程

按2.1节-2.3节所述统一对训练集和测试集计算EWMA特征、统计量特征及线路特征，形成模型的训练数据及测试数据。

3.3 建模与测试

本文基于lightgbm[12]库构建GBDT线损率预测模型。针对模型的过拟合问题，本文通过控制训练参数实现，包括回归树的最大深度、叶子节点数等。其次，在建模训练过程中采用31条不同的输电线路数据进行训练，引入多条不同环境工况特征的输电线路数据相当于实现数据增强，减小过拟合的情况。相应的训练参数如下：回归树最大深度为5；回归树的叶子节点数量为31；学习率为0.05；采用均方根误差(RMSE)作为损失函数。

4 算例验证

采用第3.2节得到的测试数据作为算例验证。采用均方根误差ERMSE作为验证误差指标，计算公式如下：

(13)

式中:Vobservedi为第i个样本的实际值；Vpredictedi为预测的线损率；N为样本总数。

为了验证模型有效性，构建以下模型作为对比：

(1) 不考虑多维特征的支持向量机模型，训练参数如下：采用径向基核函数训练，惩罚因子C设为100，r为0.1。输入为原始电能计量数据、气象和潮流数据，输出为线损率，简称支持向量机模型。

(2) 不考虑多维特征的GBDT模型，训练过程如3.3节所述，输入为原始电能计量数据、气象和潮流数据，输出为线损率，简称原始GBDT模型。

验证结果如表2所示，模型在部分验证数据的计算情况如图5所示。

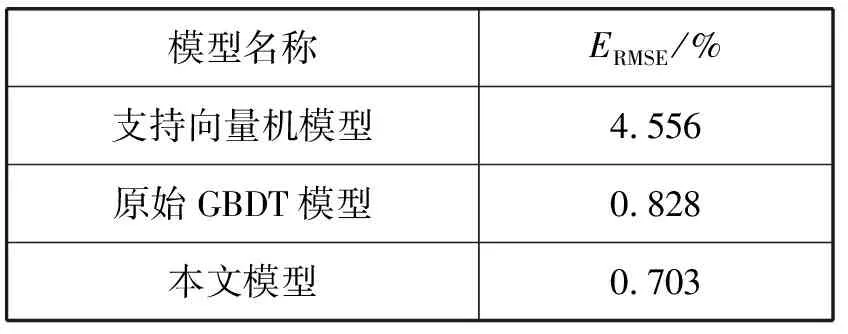
表2 模型验证测试结果

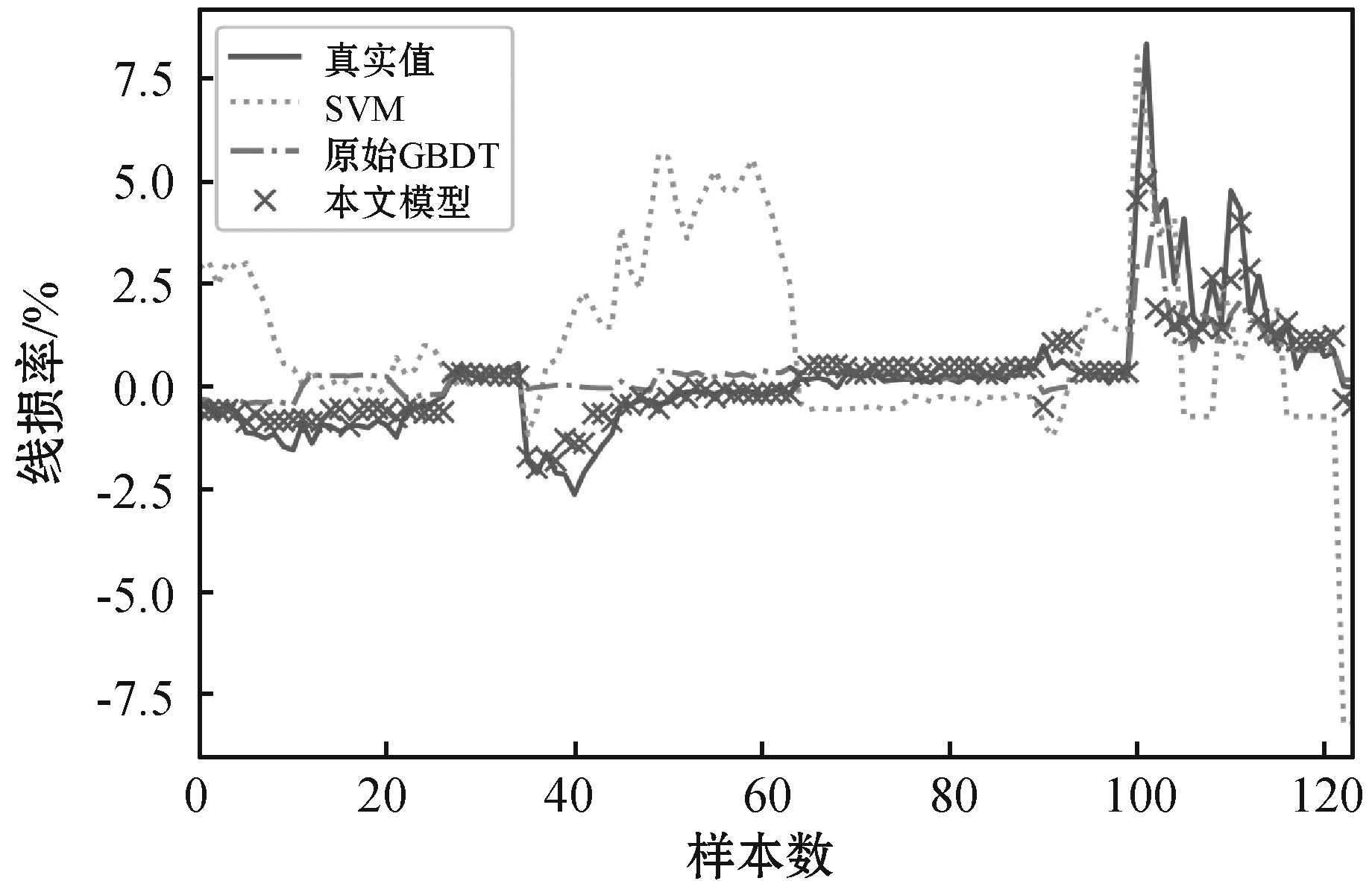
图5 模型验证结果

根据表2和图5可知，GBDT模型相较于传统的支持向量机在模型拟合上有较大优势。而相比于原始GBDT模型，采用了多维特征的本文模型在模型精度上有了进一步的提升，线损率误差指标下降15.1%，线损率误差降至0.703%，而相对于支持向量机模型，线损率误差减少84.5%，能够满足实际业务计算需求，验证了本文方法的有效性。

5 结 语

多维信息的高效利用是线损率计算模型精度的提升的关键，本文利用特征工程方法，构建输电线路线损率信息的多维特征，并利用GBDT模型构建输电线路线损率预测模型。主要结论如下：

(1) 提出了一种针对输电线路多维特征构建方法。该方法对多维信息进行挖掘，构建线损率EWMA特征、时序数据统计量特征以及线路本体的线路特征，从更精确、更细致的角度描述输电线路的实际工况及线损率的趋势情况。

(2) 结合特征工程挖掘的多维特征，通过GBDT模型对输电线路线损率进行模型拟合，构建输电线路线损率预测模型。

(3) 以某省31条500 kV输电线路实际数据为例，构建输电线路线损率预测模型。结果表明，该预测模型的线损率误差为0.703%，相比于支持向量机模型，均方根误差下降84.5%，相比于无多维特征的GBDT模型，均方根误差下降15.1%。