MSMA传感器的优化设计及试验特性研究*
鲁 军 李园君 常 强
(沈阳理工大学自动化与电气工程学院 沈阳 110159)
1 引言
材料世界一直是研究领域中令人兴奋且充满挑战的领域,随着航空航天、国防、汽车和工业部门对更先进和创新材料的需求越来越多,新一代材料比现有的常规结构和功能材料具有更好的性能。磁控形状记忆合金(Magnetically controlled shape memory alloy,MSMA)材料不仅具有磁感生应变特性,同时还具有可逆特性,在外部机械力作用下产生形变进而引起材料磁导率的改变,磁导率的改变又将引起材料的应变以及感应电压等相关物理量的变化,这为MSMA 材料应用于传感器提供了机理支持[1-2]。
本文将通过理论计算以及运用ANSYS 软件对磁路模型进行仿真计算,传感器磁路结构的设计及相关参数的选取将影响传感器的感应电压及励磁功率,为能够设计出性能优良的传感器,本文对传感器结构进行优化设计并开展试验研究。
2 MSMA 的传感器数学模型
根据磁控形状记忆合金的逆效应机理和法拉第电磁感应定律,分析MSMA 的磁路模型,建立传感器的数学模型[3-4]。
感应线圈的磁通量表达式为

根据感应电压微分方程

激振力和应力存在如下的关系式
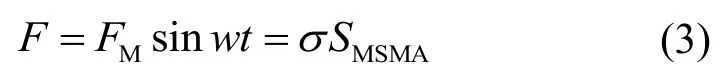
经推导,感应电压ue的表达式为
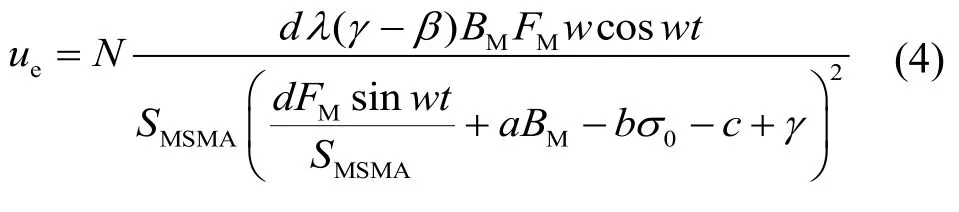
其感应电压峰峰值Ue为

式中,ΦM表示通过MSMA 材料的磁通,其磁场方向垂直于材料的变形方向;N表示线圈匝数;FM表示激振力的振幅;BM表示偏置磁场;ε表示元件的变形量;σ表示对MSMA 元件施加的压力;w表示振动频率;SMSMA表示磁控形状记忆合金的横截面积;σ0表示对材料施加的预压力;a、b、c、d、α、β、γ是未知参数。
3 磁路结构及参数设计
磁控形状记忆合金传感器的结构由传感器的铁心、气隙、永磁体、励磁线圈、检测线圈等主要部分构成。整个磁路设计的任务就是解决在需要的工作气隙中达到预定的磁场要求以及如何选择最佳磁路尺寸和最适宜的磁性材料的问题,为优化设计磁路提供依据[4]。
3.1 气隙尺寸的确定
根据磁路欧姆定律

式中,NI表示线圈的安匝数;Φ表示线圈中的磁通量;R表示磁路中总磁阻;Bδ、lδ、μδ分别表示铁心的磁感应强度、长度、相对磁导率;Bg、lg、μg分别表示永磁体的磁感应强度、长度、相对磁导率;B0、l0、μ0分别表示气隙的磁感应强度、长度、空气磁导率。
由式(6)可知,铁心材料使用硅钢片,其磁导率远大于空气和永磁体材料的磁导率,磁路中铁心的磁阻忽略不计。在安匝数不变的情况下,随着气隙的增大,气隙处的磁感应强度减小。试验所用的MSMA 的长度为2.5 mm,加护套后气隙的尺寸为3.5 mm。
3.2 永磁体材料的选取及尺寸的计算
永磁体的材料选择要考虑:①能在固定空间或环路产生试验要求在气隙处产生0.27 T 左右的磁场设定值;② 在满足设计要求的前提下,永磁体体积要尽量小。本文永磁体材料使用牌号为N52 的钕铁硼,材料剩磁为1.43~1.46 T,矫顽力为939 kA/m,最大磁能积(BH)max为398~413 kJ/m3。
本设计应用磁路定律对永磁体尺寸进行设计。根据基尔霍夫第一定律和第二定律
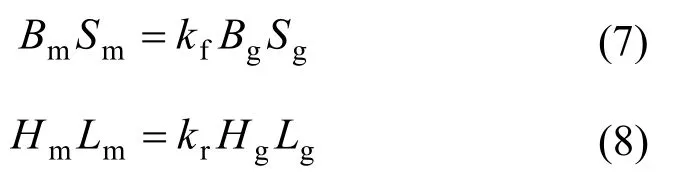
式中,kf为漏磁系数,它的取值与磁路有关,其变化范围很大,为1~20[5];kr为磁阻系数,与铁心的长度和中间气隙有关,其变化范围为1.05~1.45;Bm、Hm、Sm、Lm分别为永磁体工作点的磁感应强度、磁场强度、永磁体的横截面积及长度;Bg、Hg、Sg、Lg分别为磁路中气隙的磁感应强度、磁场强度以及气隙的横截面积、长度。
当铁心中间气隙已知时(Lg=3.5 mm),工作在最佳工作点上永磁体的Bm/Hm一般都近似等于永磁体的Br/Hc,可以得出永磁体的长度Lm为
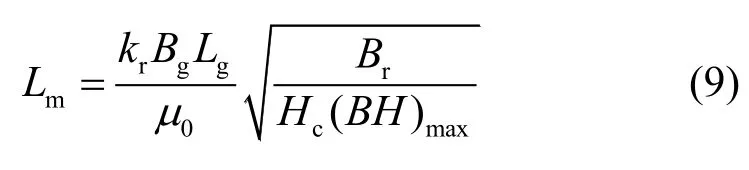
式中,Br表示剩余磁通密度;Hc表示矫顽力;通过查阅相关永磁体资料以及经验值[6]可知,漏磁系数kf=1.55,磁阻系数kr=1.35。永磁体选用N52,最终计算出永磁体的长度约为2.2 mm。
3.3 聚磁头长度的确定
励磁电流一定时,铁心聚磁头长度参数对磁场分布及磁感应强度有重要影响。图1 为聚磁铁心的结构示意图。据经验公式(10)求导可得最佳的聚磁长度s近似为5.75 mm。
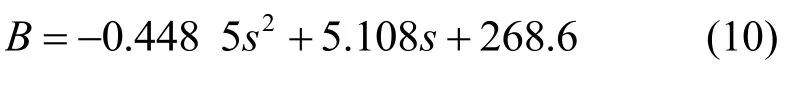
随着聚磁头长度s的增加,磁隙处磁感应强度B增长趋势微弱最后趋于稳定甚至减小,可以判断聚磁头长度s为5.75 mm 时聚磁效果最好。

图1 聚磁铁心的结构
3.4 线圈匝数的确定
本试验中采用永磁体和励磁线圈共同励磁的方式[7]。图2 为优化前后的磁路等效磁阻,磁路中气隙和永磁体的磁阻公式为

式中,Ri为各段的磁阻;li为各段导磁长度;μi为磁路中各部分材料的磁导率,μi=μ0μri;μ0为真空中的磁导率,μ0=4π×10-7H/m;μri为各段磁路的相对磁导率。

图2 等效磁路模型
优化变量如表1 所示。优化前后两种结构气隙处的磁阻大小分别为Rg=1.59×107H-1和gR′=1.14×107H-1;计算得到永磁体在磁路中磁阻的大小分别为Rm=7.2×106H-1和mR′=3.6×106H-1。

表1 优化前后设计变量值
根据安培环路定理和磁路欧姆定律,磁路中的磁通量Φ可表示为

在磁路气隙设计时,由于磁路中间是一个楔形气隙,为了让计算结果更加准确,则在计算磁通量时,根据经验先预估一个漏磁系数。通过多次比较计算值和仿真值,可得一个相对准确的漏磁系数。
由式(12)可以推导出优化前后励磁线圈的匝数分别为2 000 匝和1 575 匝。增大检测线圈匝数,会提高传感器输出的感应电压值。因此检测线圈使用0.35 mm 的漆包线,匝数初步设置为2 000 匝。
为防止线圈功率过大而产生较大的铜损,综合考虑取J=3 A/mm2,则励磁线圈中的电流I与线圈中的线径d的表达式为

根据线圈骨架尺寸可得到线圈匝数N与绕线厚度T的关系

式中,C为线圈的最大直径,取0.53 mm。
计算出优化前后线圈厚度分别为T≈12.76 mm、T≈10.5 mm。
励磁线圈的总电阻为

式中,ρ为铜的电阻率,取1.72×10-8Ω·m;W为线圈骨架的截面长度,取0.029 m;k为线圈骨架的截面宽度,取0.016 m。
经计算得出优化前励磁线圈电阻R1=23.77 Ω,优化后励磁线圈电阻R2=17.25 Ω,根据P=I2R,计算得出优化后的励磁功率减少了27.4%。
4 ANSYS Maxwell 仿真分析
MSMA 传感器的3D 电磁仿真[8-12]模型如图3所示。永磁体单独励磁以及永磁体和励磁线圈共同励磁铁心中的磁通密度矢量分情况分别如图4、5所示。永磁体单独提供的磁通密度在气隙处可达0.30 T,当励磁线圈的磁动势NI=1 575 A 时,气隙处的磁通密度能够达到0.6 T。
图3 3D 电磁仿真模型
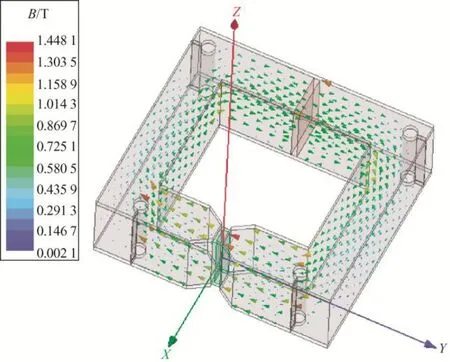
图4 单独永磁体铁心磁通密度矢量分布图
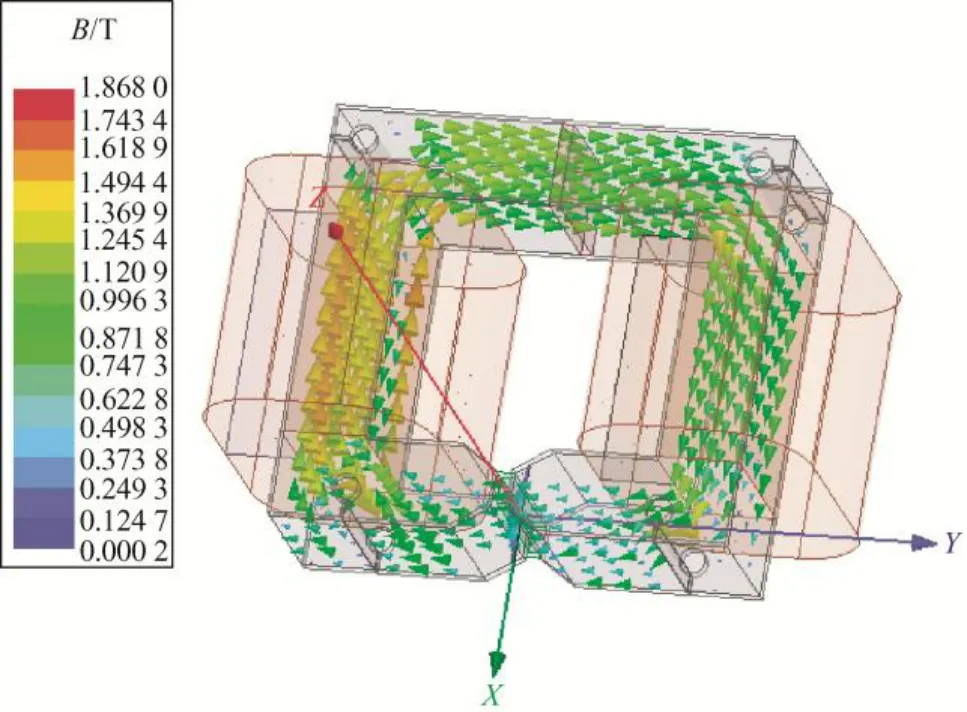
图5 励磁线圈通电后的磁场矢量分布图
5 试验结果与验证
MSMA 传感器的试验系统如图6 所示。MSMA传感器输入分别为激振器的频率、幅值及可变磁场,输出为检测线圈的感应电压值。
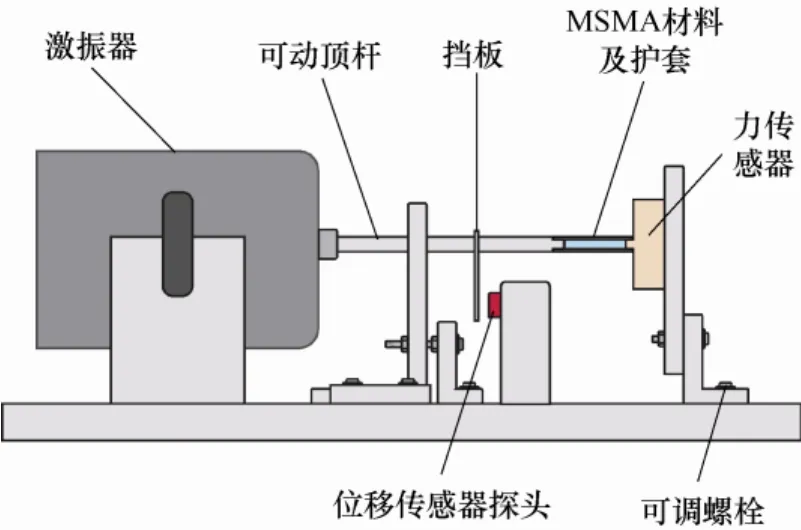
图6 MSMA 传感器的试验系统
5.1 传感器感应电压与偏置磁场的关系
输入信号激振力频率为100 Hz,大小为0.5 N,偏置磁场为310 mT 时,输出感应电压波形如图7所示。感应电压的输出峰-峰值约为110.6 mV。
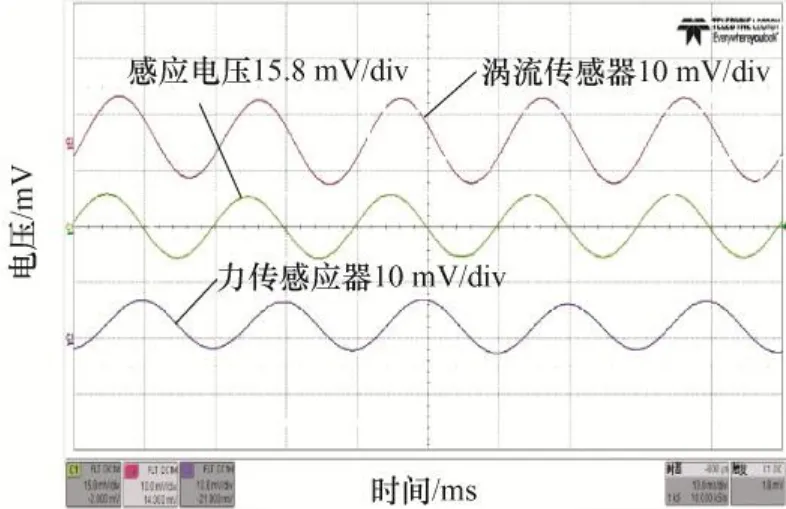
图7 偏置磁场为310 mT 时,试验的输出波形
在力的幅值和频率保持不变情况下,改变偏置磁场这一变化量,传感器输出的感应电压的试验值和计算值比较如表2 所示。随着外加磁场的不断增强,感应电压的峰-峰值也不断变大。
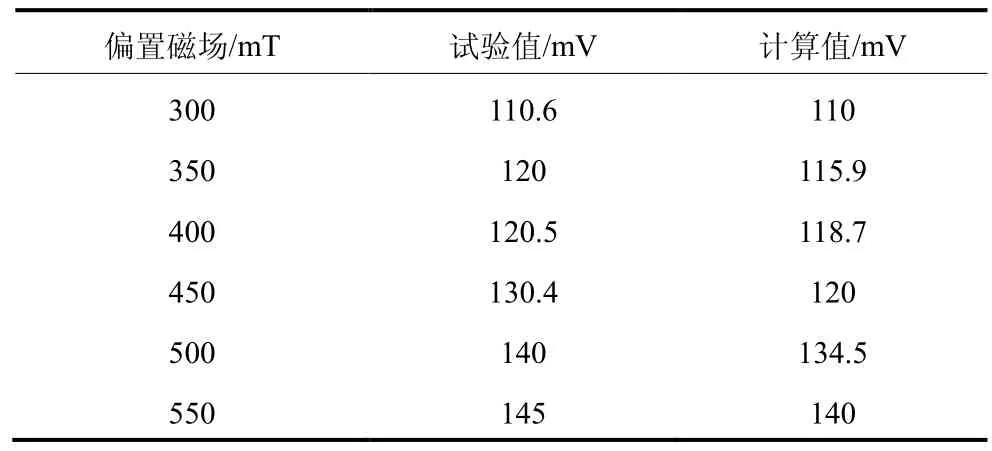
表2 磁场改变时传感器感应电压试验值和计算值的比较
5.2 传感器感应电压与激振力幅值的关系
当输入信号频率为150 Hz,大小为0.55 N,偏置磁场为310 mT 时,感应电压的输出峰-峰值约为174.6 mV,试验波形如图8 所示。
通过改变力的幅值,而不改变激振力频率和磁场强度,对输出感应电压信号进行采集分析并与计算值进行比较,如表3 所示。感应电压的峰-峰值随着幅值的不断增大而增大,并且基本呈线性关系。

图8 激励力大小为0.55 N 时,试验的输出波形

表3 幅值改变时传感器的感应电压试验值和计算值的比较
5.3 传感器感应电压与激振力频率的关系
通过功率放大器调节激振力的大小为0.35 N、偏置磁场为0.33 T,激振力频率为120 Hz,试验数据如图 9 所示。感应电压的输出峰-峰值约为128 mV。

图9 激励力频率为120 Hz 时,试验的输出波形
只改变力的频率,力的幅值和偏置磁场保持不变,传感器输出的感应电压的试验值和计算值比较如表4 所示。可以看出,理论值与试验值基本吻合。并且随着力的频率不断增大,感应电压的峰-峰值随之变大,两者之间呈现正比例关系。

表4 频率改变时传感器感应电压试验值和计算值的比较
5.4 传感器的优化结果比较
在相同试验条件下,对于优化前后的MSMA传感器波形比较如图10 所示。根据试验数据,输入信号激振力的频率150 Hz、振幅0.35 N 以及偏置磁场0.32 T 得到输出的感应电压信号。优化后传感器输出的电压值大于优化前的感应电压值,验证了传感器结构优化后的合理性。
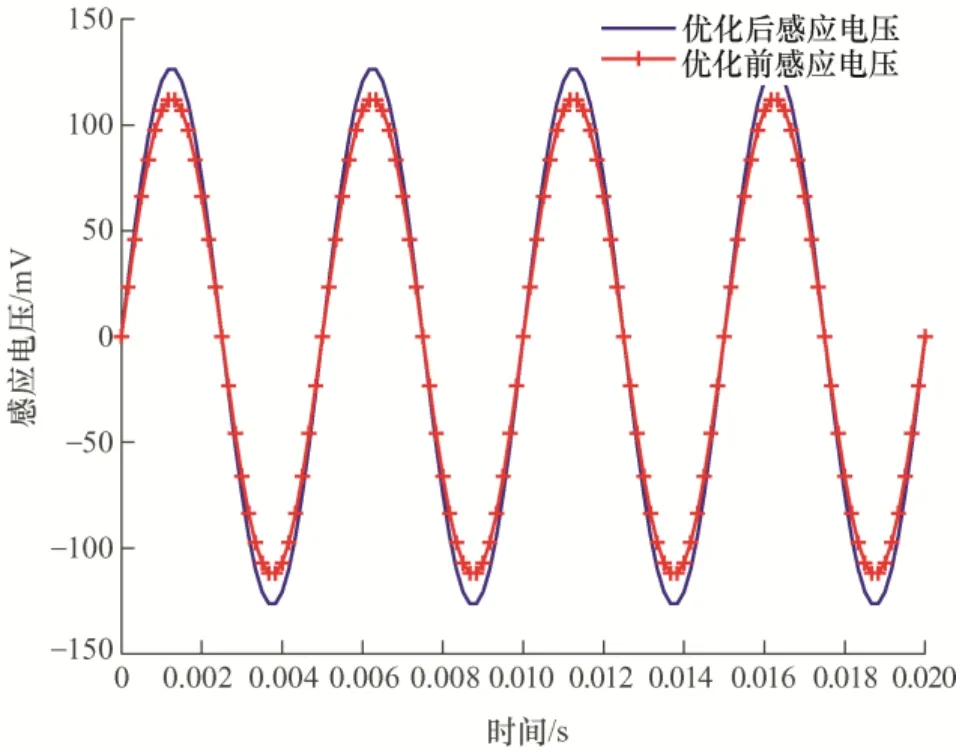
图10 优化前后感应电压的比较
6 结论
本文采用磁路欧姆定律、基尔霍夫定律以及经验取值的方法分别对MSMA 传感器的励磁线圈、永磁体长度、气隙长度、聚磁头长度进行优化设计,并对MSMA 传感器的磁场进行有限元仿真,确定传感器的结构,为MSMA 传感器的应用提供了设计依据。现得出以下结论。
(1) 试验理论计算值与试验值吻合。
(2) 优化后的传感器中感应电压的幅值提高了12.9%。
(3) 优化后的励磁功率减少了27.4%。

