模块化细轭部磁通切换永磁直线电机及其控制*

程 明 张邦富 王飒飒 王 伟

(1.东南大学电气工程学院 南京 210096；2.东南大学盐城新能源汽车研究院 盐城 224007)

1 引言

随着城市化的进展，可使用的建筑土地越发有限，建筑物也逐渐向高层甚至超高层发展。世界最高的建筑物将达到甚至超过600 m[1]。因而，高效的电梯运输系统对这些超高层建筑至关重要。现有商业化的曳引式电梯系统在同一井道中最多运行两个轿厢[2]，导致乘客等待时间长，极大地制约了电梯的运载能力。增加电梯的数量可以提高电梯运载能力，减少乘客等待时间，但电梯系统所占面积可高达建筑面积的40%[2]，使得建筑物的经济性下降。此外，曳引式电梯通过缆绳连接轿厢、曳引机和配重，随着建筑高度的增长，缆绳长度和重量不断增加，缆绳消耗的能量以及带来的垂直震荡问题越发明显。当建筑高度达到一定程度，缆绳的机械强度必然不足，曳引式电梯也将不复适用。

为了解决上述曳引式电梯存在的问题，三十多年前就已有学者提出无绳电梯(Ropeless elevator)[3]。无绳电梯的轿厢由直线电机直接驱动，理论上提升高度不受限。无绳电梯同一井道中可以运行多个轿厢，提高电梯运载能力并减少乘客等待时间。因此，电梯所占建筑面积大大减小。此外，无绳电梯不再局限于垂直运动，还可以水平运行，在智能化建筑中具有应用前景。对比传统曳引式电梯，无绳电梯省去了缆绳和变速齿轮等，运行更安静。值得一提的是，由于无绳电梯所涉及技术复杂，至今尚未大规模商业运行。德国ThyssenKrupp 公司的无绳电梯——MULTI 系统仍处于测试阶段[4]。

无绳电梯所用直线电机主要有感应直线电机、同步直线电机和开关磁阻直线电机[5]。感应直线电机虽结构简单，但推力密度低、效率低、控制复杂，不适合电梯类长行程场合[6-8]。对比感应直线电机，永磁同步直线电机具有更高的推力密度和效率[9-11]。为了节约成本，一般永磁体贴在轿厢侧，铁心和电枢绕组沿井道铺设。ThyssenKrupp 公司的MULTI 系统采用的是两台双边无铁心永磁直线电机驱动轿厢[4]。随着井道高度的增加，电机成本会急剧增加。此外，为了提高无绳电梯载荷，文献[12-13]中提出采用超导同步直线电机，超导体和相关冷却装置位于轿厢侧。这增加了系统的复杂性。开关磁阻直线电机结构简单、可靠，成本低，所以文献[14-16]将双边开关磁阻直线电机应用于垂直驱动场合。然而，与感应直线电机类似，开关磁阻直线电机的推力密度不高。因此，探索一种结构简单可靠、成本低、推力密度高的直线电机，对无绳电梯驱动具有重要意义。

磁通切换永磁(Flux-switching permanent magnet，FSPM)电机的电枢绕组和永磁体都置于定子侧，而转子由导磁铁心构成。简单可靠的结构、与转子永磁同步电机相近的转矩密度和效率使得FSPM 电机得到日益广泛的关注[17-19]。将FSPM 电机展开，可以得到其直线形式[20-22]。在无绳电梯、轨道交通等长行程应用场合中，采用FSPM 直线电机具有高效率和低成本等优点。值得说明的是，为了节省成本，FSPM 直线电机一般采用短初级动子结构，即永磁体和电枢绕组均位于短初级动子侧，放在轿厢内，而长次级定子仅由铁心组成，沿井道铺设。

本文针对无绳电梯应用场合提出一种模块化细轭部磁通切换永磁直线(Modular thin yoke linear flux-switching permanent magnet，MTYLFSPM)电机并搭建驱动控制系统[23]。该电机是双定子结构，沿井道铺设，而初级动子采用模块化结构，置于电梯轿厢侧。文中将阐明所提出电机结构、工作原理以及极距比对电机性能的影响。以一台MTYLFSPM电机为例，基于Simulink 建立该电机的模型、系统仿真模型，并进行模拟电梯上下运行仿真分析。最后，基于试验样机验证电机性能参数、电机模型准确性和进行电梯模拟运行试验。

2 电机结构和工作原理

本文提出的MTYLFSPM 电机如图1 所示。直线电机是双边结构，两块次级定子铁心将动子夹在中间。两块次级定子铁心错开半个定子极距τs/2 用以增强气隙磁场和推力，同时削弱推力波动。动子由三个动子单元组成，每个动子单元构成电机的一相，其长度为2τm，即两倍的动子极距长。相邻模块间距离为λ1=(m±n/3)τs或者(m±n/6)τs，m、n是正整数。可以结合电机性能指标以及动子长度最小原则来确定m和n。三个动子单元中永磁体交替充磁，充磁方向平行于电机运动方向。特别强调的是，区别于传统FSPM电机，本文电机的动子铁心轭部不再是主磁路部分而是机械连接部件。轭部中所开安装孔是为了安装支撑杆，支撑整个动子，保证气隙均匀。在保证机械强度的前提下，轭部可以尽量做细。因而，本文称之为细轭部结构。

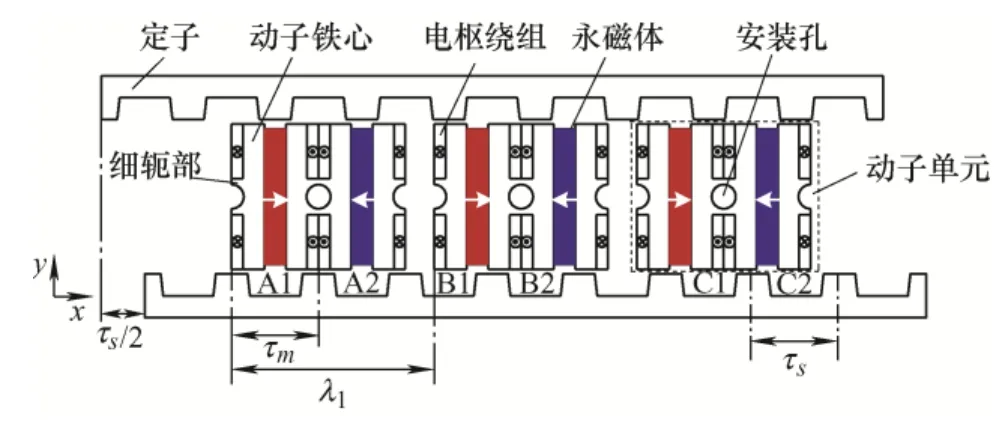
图1 MTYLFSPM 电机截面图

下面以极距比τm/τs=1 的MTYLFSPM 电机为例，说明其工作原理。开路下电机四个特征位置处的磁场分布示意图如图2 所示。图2a～2d 分别对应绕组磁链正向最大、等于零、负向最大和再次等于零。由此可见，随着动子位置的变化，电机绕组磁链交替变化并感应出反电势。通入对应的交流电，可以使电机输出有效推力。

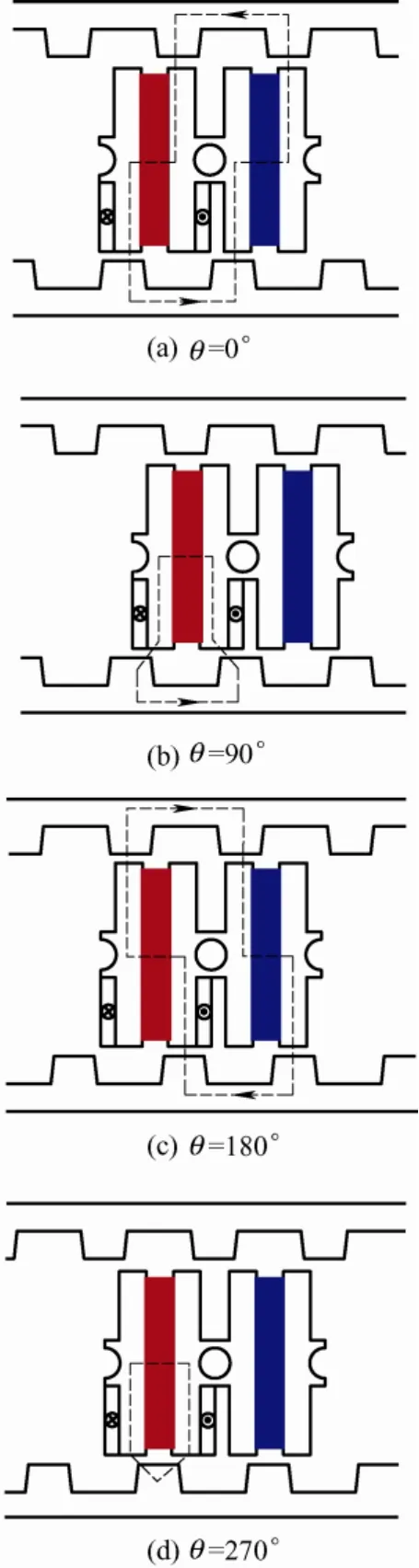
图2 电机运行原理

基于有限元法，针对不同τm/τs下的MTYLFSPM电机进行优化设计，其关键结构参数如表1 所示。优化结果如图3 所示。图中推力波动率的定义为一电周期内推力的峰峰值占推力均值的比例。τm/τs=7/6电机的推力波动率为7.7%，其余极距比下电机的推力波动率均小于5.5%。τm/τs=6.5/6 电机的推力是最大的，而τm/τs=1 电机的推力略小于τm/τs=6.5/6 电机。因此，本文的后续内容以τm/τs=6.5/6 电机为研究对象。

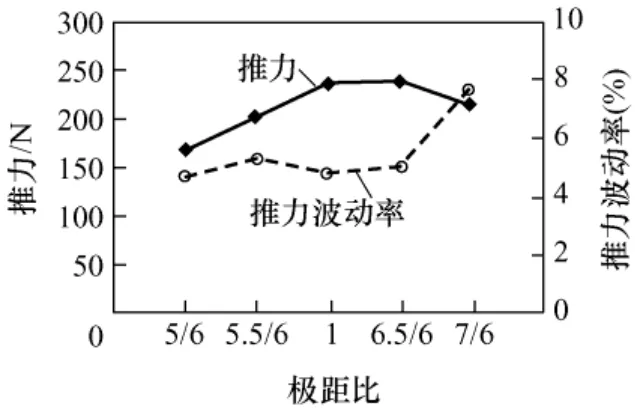
图3 推力和推力波动率

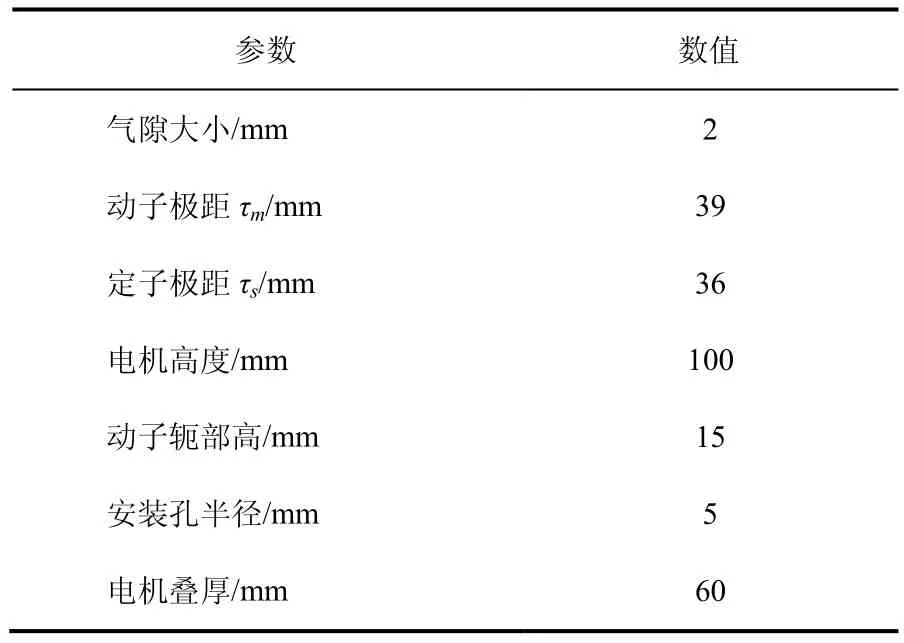
表1 MTYLFSPM 电机主要参数

3 电机建模和控制策略

3.1 电机建模

永磁电机结构复杂并存在高饱和情况，为了研究其性能，常采用控制电路与有限元模型耦合仿真的方式[24]。但是，该方法耗时长，不便于控制器参数调节。文献[25]基于d、q轴建立了考虑磁饱和、空间谐波和铁耗影响的高精度电机模型。本文采用该方法进行电机建模，并做了相应改进以提高建模效率。

值得说明的是，由于样机加工过程中没能很好地控制加工精度，导致电机气隙不均匀且各相动子单元在y方向上存在偏移。因此，针对τm/τs=6.5/6电机进行建模，考虑了这些加工误差因素。

基于磁链的电机电压、推力方程为[26]

式中，Rs是相电阻，x是动子位移，Wm是电机内存储的磁能。d轴磁链ψd、q轴磁链ψq和Wm都与d轴电流id、q轴电流iq、动子位置角θ密切相关。

本文根据图4 所示框图建立电机模型。因为电机动子体积小且额定运行频率不高(＜30 Hz)，铁耗很小，因此所建电机模型中没有考虑铁耗影响。首先，建立三维表格ψd(id,iq,θ)和ψq(id,iq,θ)。图5a 和图5b 分别为电机动子在一固定位置时，ψd，ψq随id、iq变化的曲面。图5 中黑点对应有限元仿真值。值得注意的是，由于直线电机动子垂直上下运动，为了克服动子重力，推力始终朝上。因此，这里仅考虑id、iq处于第二象限的情况。

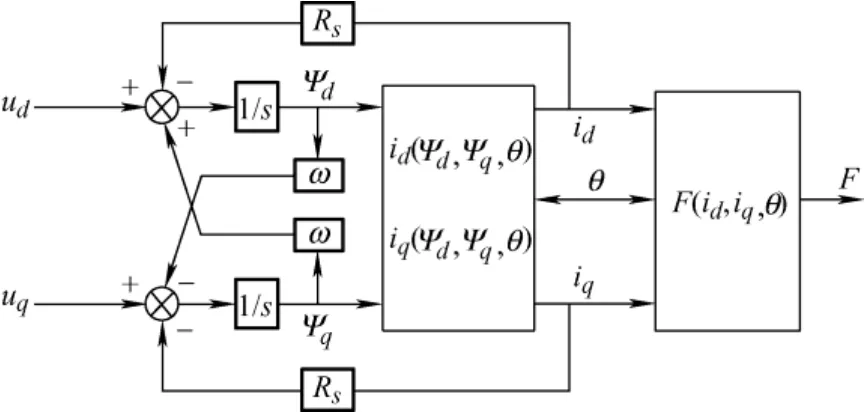
图4 电机模型框图

图5 d、q 轴磁链

为了获得id(ψd,ψq,θ)和iq(ψd,ψq,θ)，文献[24]中先建立三维表格ψd(id,iq,θ)和ψq(id,iq,θ)，再利用寻优插值法反推得到id(ψd,ψq,θ)和iq(ψd,ψq,θ)，运算过程较复杂。本文先利用径向基函数(Radial basis function)拟合不同θ下id(ψd,ψq)和iq(ψd,ψq)，后再建立三维表格id(ψd,ψq,θ)和iq(ψd,ψq,θ)。上述过程简洁，运算迅速。图6a 和图6b 分别为根据图5 曲面得到的电机动子在一固定位置时，id、iq随ψd，ψq变化的曲面。

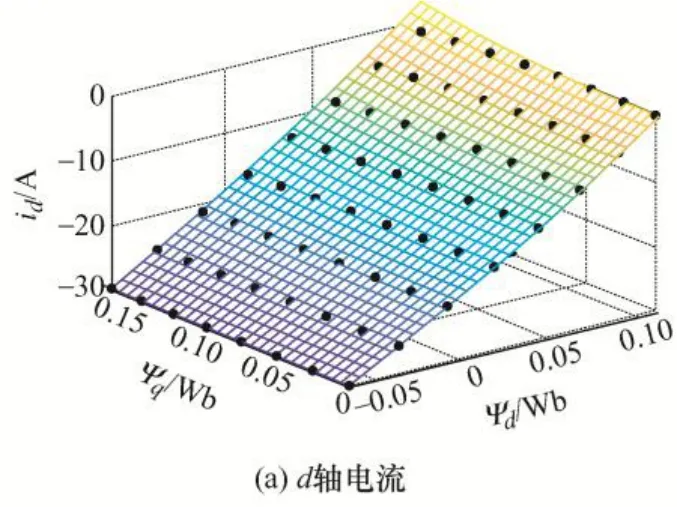
图6 d、q 轴电流

为了得到式(2)所示推力方程，还需要ψd、ψq和Wm对x的导数。这里采用向后差分先求取ψd、ψq和Wm对x的导数，再建立对应的三维表格。图7 是电机动子在一固定位置时，Wm随id、iq变化的曲面。

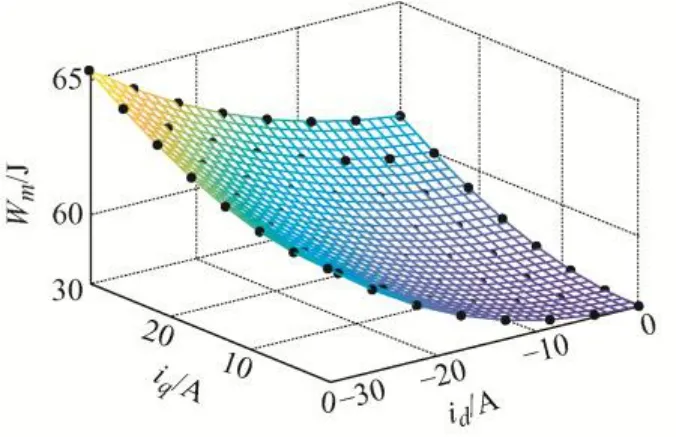
图7 磁能

利用前面所得数据建立目标直线电机的Simulink 模型，进行了仿真分析。图8 中对比了不同正弦电流下的推力波形。因为MTYLFSPM 电机凸极性不明显，故采用id=0 控制。图中所示电流指id=0 时的iq。从图8 中可知，Simulink 模型和有限元模型得到的推力波形很吻合，验证了所建电机模型的准确性。另外，加工误差显著增加了电机的推力波动率。

图8 推力波形

此外，MTYLFSPM 电机动子垂直运动时的机械运动方程可表示为

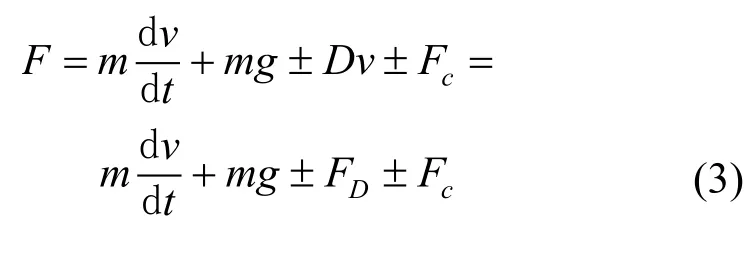
式中，m为计及负载的动子总质量，v为动子速度，g为重力加速度，D为黏滞摩擦因数，FD为黏滞摩擦力，FC为库仑摩擦力。当动子向上运行时，式(3)中“±”取“+”，而向下运行时取“-”。经试验测量，D约为46 N/(m/s)，FC约为90 N。

3.2 控制策略

由于样机加工误差大，导致最终的推力波动较大。此外，导轨滑块与直线导轨之间较差的匹配安装，相应摩擦力会随移动位置、速度的变化而变化。这里将推力波动和摩擦力统一视为一种扰动。为了抑制扰动的影响，提高控制品质，本文采用自抗扰控制(Active distance rejection control，ADRC)技术[27]。ADRC 技术将所有不确定因素作用归结为一种扰动，并用控制对象的输入输出数据对扰动进行估计并且给予补偿。基于ADRC技术的MTYLFSPM电机的控制系统如图9 所示。

图9 MTYLFSPM 电机控制系统

图9 中d*、v*分别是结合电梯运行情况而设定的给定位移、给定速度，d是由磁栅尺反馈得到的实际位移[28]。ADRC 控制器使用扩张状态观测器对扰动进行观测并补偿到给定的iq*。采用id=0 矢量控制，利用空间矢量脉宽调制(Space vector pulse width modulation，SVPWM)产生三相桥驱动信号。

4 系统仿真

根据上述电机模型和控制策略，建立了基于Simulink 的MTYLFSPM 电机控制系统模型，并进行模拟电梯上下运行仿真分析，仿真结果如图10 所示。

图10a 是模拟电梯从一楼运行到二楼，再运行到三楼后直接下降到一楼的运行情况。每层楼高为0.5 m。在整个运行过程中，给定位移与实际位移的误差控制在0.3 mm 以内，体现了ADRC 技术的良好性能。从速度曲线可知，电梯运行中经历了加速、恒速和减速三个过程。电梯恒速运行时，速度为最大速度0.2 m/s。在电梯向下运行时，由于摩擦力较大且与电梯重力反向，直线电机所需出力比向上运行时明显减小，因此电流幅值比向上运行时显著降低。

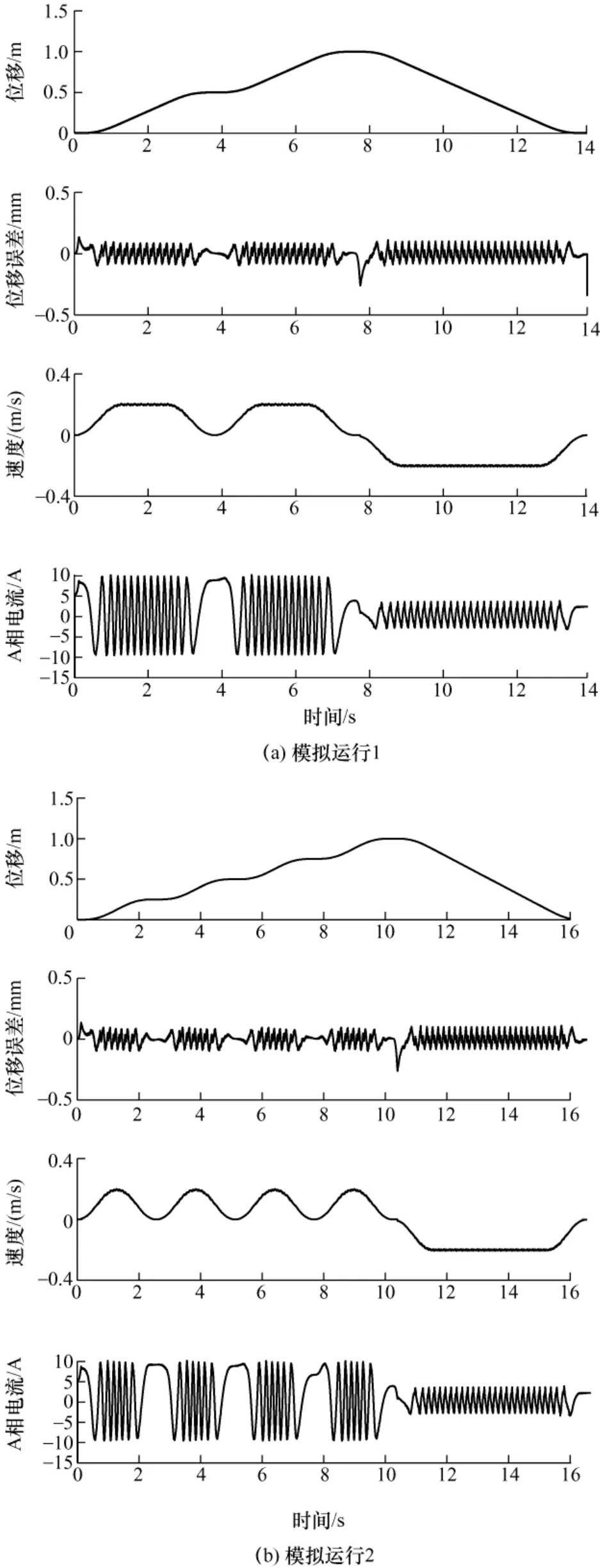
图10 电梯模拟运行

图10b 是模拟电梯从一楼运行到五楼，每个楼层都停靠，后直接下降到一楼的运行情况。每层楼高为0.12 m。在整个运行过程中，误差始终控制在0.3 mm 以内。从速度曲线可知，电梯运行中只经历了加速和减速两个过程。电梯是加速运行到最大速度0.2 m/s 后开始减速运行。这是由于电梯运行位移太短的缘故。

从上面的仿真结果可知，所建立的MTYLFSPM电机控制系统模型可以很好地模拟电梯运行情况。

5 试验验证

为了验证上述理论分析和仿真结果的正确性，制造了1 台τm/τs=6.5/6 的MTYLFSPM 电机，并搭建了基于dSPACE 的控制系统平台，如图11 所示。

图11 MTYLFSPM 电机样机及控制平台

图12 为样机的定位力的有限元仿真值和实测值。两者波形较为吻合，峰峰值达到100 N。为了比较，理想电机参数下的定位力仿真波形也在图中显示，其峰峰值为14 N。可见，样机加工误差明显增加了定位力。

图12 仿真与试验定位力波形

电机速度v=1.33 m/s 时的空载反电势的仿真和试验波形分别如图13a 和图13b 所示。仿真结果考虑了铁心叠压系数和电机端部效应的影响。A 相试验反电势的峰峰值比仿真所得峰峰值小约5%，而B、C 相试验反电势的峰峰值比仿真所得峰峰值大约3%。产生误差主要是因为样机的加工误差在仿真模型中没能全部考虑。有些加工误差无法准确测量得到。

图13 v=1.33 m/s 空载反电势

图14 电梯模拟运行试验

与系统仿真对应的模拟电梯上下运行的试验波形如图14 所示。模拟电梯从一楼运行到二楼，再运行到三楼后直接下降到一楼的运行情况，如图14a所示。从位移误差波形可知，在整个运行过程中，给定位移与实际位移的误差控制在0.5 mm 以内，与仿真分析结果相近。以0.2 m/s 恒速运行时，电流幅值约为10 A，与仿真结果相一致。但试验所得的电流幅值比仿真值波动更为明显，这是因为加工误差导致样机动子在不同位置处的定位力、摩擦力系数会有些许变化，而仿真模型中没能完全考虑这些变化。模拟电梯从一楼运行到五楼，每个楼层都停靠，后直接下降到一楼的运行情况如图14b 所示。从电梯模拟运行波形中可知，位移误差一直保持在0.8 mm 以内，略大于仿真结果。将仿真与试验结果进行比较可知，两者波形比较吻合，这也验证了所建电机模型和控制系统模型的准确性。

6 结论

本文提出了一种针对无绳电梯应用场合的模块化细轭部磁通切换永磁直线电机。分析了极距比对电机推力和推力波动率的影响，确定极距比为6.5/6的电机性能最佳。针对该电机，建立考虑饱和、空间谐波的准确电机模型和系统仿真模型。模拟电梯上下运行的仿真分析验证了模型的准确性。基于试验样机和试验控制平台，完成了定位力、空载反电势、电梯模拟运行的试验研究。试验结果与仿真结果吻合较好，说明本文提出的电机及其控制系统为无绳电梯驱动提供了一种可行的解决方案。