基于谐波提取器的永磁同步电机谐波抑制方法*
金 石 朱 熙 金无痕 张凤阁
(沈阳工业大学电气工程学院 沈阳 110870)
1 引言
永磁同步电机因其效率高、功率密度高、气隙磁通高、控制结构简单等特点而广泛应用于数控机床、电力传动及航空航天等场合。然而由于电机绕组分布形式、齿槽效应以及逆变器死区效应等非线性因素会使电机定子绕组电流产生谐波,使电机转矩、转速产生波动,增大了电机的额外损耗,影响电机运行的稳定性。
永磁同步电机定子绕组电流谐波的类型分为两类:时间谐波和空间谐波。时间谐波是由逆变器非线性因素如死区效应和开关管压降引起的;空间谐波是由电机结构如绕组分布形式,磁路饱和效应等因素引起的。永磁同步电机电流谐波以 6k±1 次谐波形式存在,其中主要以5、7 次谐波含量较高。针对电机定子电流存在谐波的问题,国内外学者主要从两个方面来进行谐波抑制的研究工作。一是从电机控制策略来入手,通过谐波补偿策略来进行谐波抑制,主要抑制策略包括谐波电压补偿法、多旋转PI(Proportion integration,PI)控制[1-2]、复矢量控制[3]、重复控制[4-5]、自抗扰控制[6]、比例谐振控制[7-9];二是从电机本体结构入手,如斜槽[10],优化永磁体形状、磁路及定子绕组类型来达到电流谐波抑制的目的。其中谐波电压注入是最为广泛的一类谐波抑制策略,谐波电压注入的主要问题在于谐波电流的检测,因为传统的PI 控制器不能对交流量进行无误差跟踪,因此对于交流信号的提取,一般从两种角度来考虑,一种是根据谐波在对应次数的旋转坐标系下表现为直流量,通过坐标变换把谐波交流分量转换为直流分量,再通过低通滤波器来获得谐波直流分量;另一种是通过将能跟踪交流量的控制器与PI控制器结合达到谐波交流量提取。文献[11]采用多旋转坐标变化来提取谐波电流的直流分量,其主要原理是通过将要抑制的谐波对其进行坐标变换到对应次数的d-q坐标系下,把该交流谐波分量变为直流谐波分量,最终通过低通滤波器实现谐波补偿量的提取。但由于加入了多个PI 控制器,导致该方法算法复杂,参数整定困难。文献[12]在传统多旋转PI控制的谐波电流检测模块进行改进,用闭环电流平均值法来代替低通滤波器,解决了因低通滤波器所带来的动态响应时间长,稳态误差大的问题。文献[13]采用对死区时间产生的误差进行补偿的方法,根据误差电压与电机相电流极性的关系,来补偿逆变器死区时间的影响,抑制由死区效应造成的谐波。但由于零电流箝位现象的影响,不能准确地判断电机相电流极性,使补偿精度降低,影响谐波抑制的效果。文献[14]采用一种线性插值法的数字滤波器对分数阶延时环节进行逼近,从而使重复控制器的谐振频率和电机电流实际谐波频率相吻合,提高了重复控制器对电流谐波的抑制能力,但抑制效果受低通滤波器的位置和线性插值法的精度所限。文献[15]提出了基于重复控制内模的双二阶广义积分器的谐波检测结构,通过在双二阶广义积分器中嵌入重复控制内模,在基波和其他次谐波段产生增益,从而获得特定次频率的谐波信号,对应用到电机谐波检测具有借鉴意义。
针对传统PI 控制器不能很好地跟踪交流信号的问题,本文提出了一种基于正、负序谐波提取器的新型谐波电流检测结构,通过提取电机相电流主要存在的5 次负序、7 次正序谐波交流分量,将提取的谐波交流分量注入到输出电压中,来达到谐波抑制的目的,最后通过仿真来验证该方法的有效性。
2 PMSM 谐波数学模型
永磁同步电机在基波d-q旋转坐标系下的电压方程为
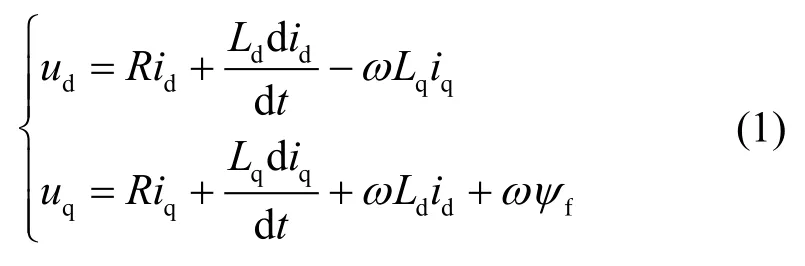
式中,R为定子电阻;id,iq分别为定子d轴、q轴电流;ud,uq分别为定子d轴、q轴电压;Ld,Lq分别为d轴、q轴电感;ψf为永磁体磁链;ω为基波的电角速度。
永磁同步电机为三相三线系统,定子绕组为星形连接且没有中性线引出,因此在电机定子绕组的电流n次谐波中不存在偶次谐波和3k(k=1,2,3,…)次谐波,且当n=6k+1(k=1,2,3,…)时,谐波电流的旋转方向与基波电流旋转方向一致,可认为是正序谐波;当n=6k-1(k=1,2,3,…)时,谐波电流旋转方向与基波旋转方向相反,可认为是负序谐波。只考虑5、7 次谐波的存在,则在abc 三相电流静止坐标系下,以a 相电流为例,a 相电流可表示为
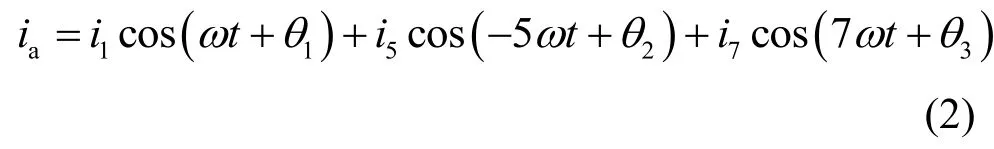
式中,i1、i5、i7分别为基波、5 次、7 次谐波电流的幅值;θ1、θ2、θ3分别为基波、5 次、7 次谐波的初始相位角。
电机定子电流从abc 三相静止坐标系变化到d-q旋转坐标系下,通过Clark 变换可得电机d-q旋转坐标系下的电流方程

式中,id1、iq1分别为基波电流在d轴、q轴的分量;id5、iq5分别为5 次谐波电流在d轴、q轴的分量;id7、iq7分别为7 次谐波电流在d轴、q轴的分量。由式(3)可知,在d-q旋转坐标系下基波变为直流分量,5 次、7 次谐波分别变为6 次负序、正序交流量。
3 基于谐波提取器的谐波注入法
3.1 谐波提取器原理
对于一个正弦信号e(t)=Asin(ω0t+φ),其幅值积分为y(t)=Atsin(ω0t+φ),把正弦信号延时90°后,可得到正弦信号的辅助信号x(t)=Acos(ω0t+φ),对上述三个信号进行拉普拉斯变换可得
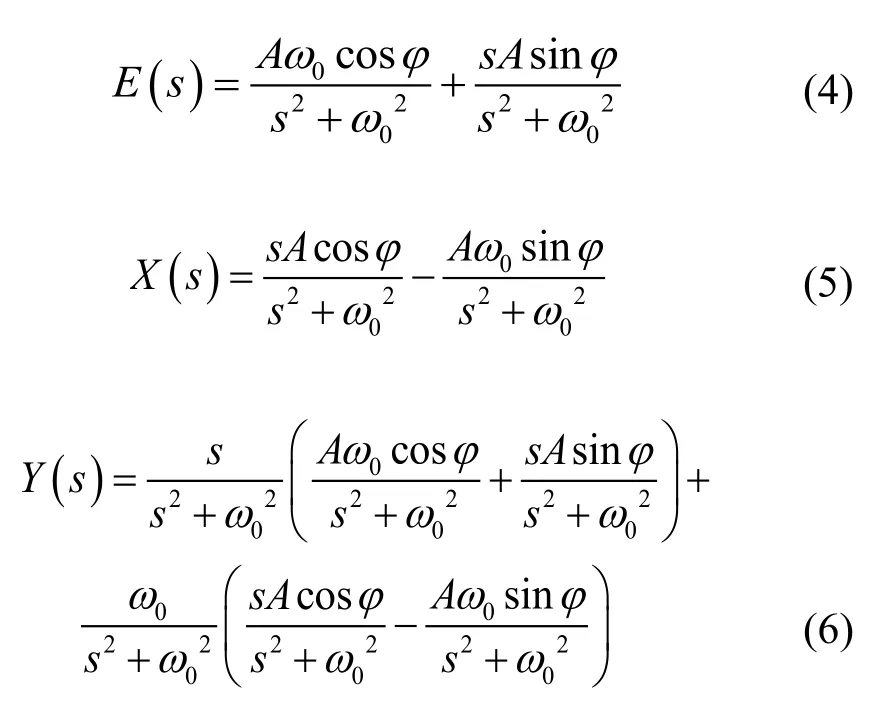
式中,E(s)、X(s)、Y(s)分别为e(t)、x(t)、y(t)的拉普拉斯变换。
由式(4)~(6)可得到传递函数
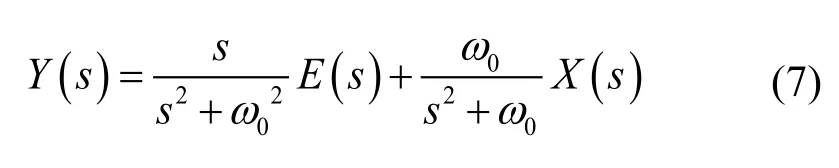
式中,E(s)、X(s)作为输入量,Y(s)作为输出量,可以看出传递函数式(7)具有频率选择特性。可绘制出正序基波提取器的结构框图,如图 1所示。

图1 正序基波提取器结构图
图1 中,k为反馈系数,其取值与正序基波提取器带宽有关,k值越大,则在所选频率处带宽越宽,相位偏移就越小,且更加缓慢,但正序基波提取器的滤波效果也会越差。
其闭环传递函数为
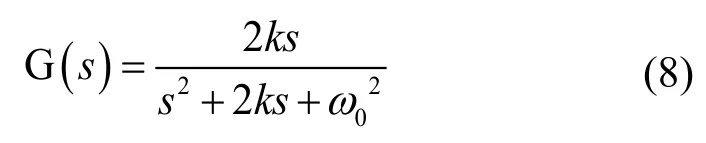
以频率为 50 Hz 为例,当ω0=100π时,k=1,15,4 0,60 时,闭环传递函数 G(s)的伯德图如图2 所示。

图2 正序基波提取器的伯德图
由图2 可知,正序基波提取器在所给频率50 Hz处具有较大增益,因此正序基波提取器可以对相同频率的正弦信号进行无静差跟踪,达到检测谐波的目的。
通过设置正序基波提取器的角速度ω可以得到对应次数的谐波提取器,当ω=6kω0时(ω0为基波对应的角速度),得到6k+1 次正序谐波提取器;当ω=-6kω0时,得到6k-1 次负序谐波提取器。以7 次正序谐波提取器为例。图3 为永磁同步电机在d-q旋转坐标系下使用7 次正序谐波提取器提取7次谐波分量的控制框图。
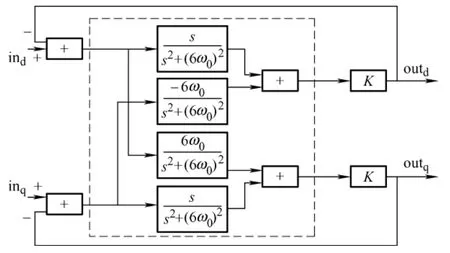
图3 d-q 坐标系下7 次正序谐波提取器控制框图
3.2 基于谐波提取器的PMSM 谐波注入矢量控制系统
系统采用传统的id=0 矢量控制,使用正、负序谐波提取器从d、q轴分别提取7 次正序谐波电流和5 次负序谐波电流。将提取到的谐波电流串联一个PI 控制器并注入到参考电压中,达到谐波抑制的目的。
图4 为基于正、负序谐波提取器与电压补偿策略的永磁同步电机谐波电流抑制的控制框图。
4 仿真分析
为了验证基于谐波提取器的电压补偿策略的可行性与有效性,在Matlab/Simulink 平台上进行基于正、负序谐波提取器的电压补偿算法的PMSM 矢量控制系统仿真模型搭建。采用的具体参数为:定子电阻R=1.85 Ω;交、直轴电感Ld=Lq=45 mH;极对数np=24;永磁体磁链ψf=1.65 Wb ;转动惯量J=3 kg · m2;死区时间td=6 μs,IGBT 开通时间ton=0.9 μs,IGBT关断时间toff=1.3 μs 。
仿真时考虑逆变器非线性因素对电机定子电流产生的影响,给定转速n*=50 r ·min-1,在两种负载下,T1=1000 N · m,T2=700 N · m进行仿真。得到的相电流波形及相电流频谱分析结果如图5~8所示。


图5 T1=1000 N · m 时不加补偿策略的相电流波形及频谱分析

图6 T1=1000 N · m 时加入补偿策略的相电流波形及频谱分析

图7 T2=700 N · m 时不加补偿策略的相电流波形及频谱分析

图8 T2=700 N · m 时加入补偿策略的相电流波形及频谱分析
图为T1=1000 N · m时不加补偿策略的相电流波形及频谱分析;图6 为T1=1000 N · m 时,加入补偿策略的相电流波形及频谱分析;图 7 为T2=700 N · m时,不加补偿策略的相电流波形及频谱分析;图8 为T2=700 N · m时,加入补偿策略的相电流波形及频谱分析。
由图5、6 可知,在T1=1000 N · m 时,在加入基于谐波提取其的谐波抑制策略后,总谐波畸变率THD 由7.86%降低为3.32%,其中5 次谐波畸变率由6.46%降为1.75%,7 次谐波畸变率由2.92%降为0.73%。
由图7、8 可知,在T2=700 N · m 时,在加入谐波抑制策略后,总谐波畸变率THD 由8.34%降为3.78%,其中,5 次谐波畸变率由6.34%降为1.28%,7 次谐波畸变率由2.48%降为1.14%。
因此,基于谐波提取器的PMSM 谐波抑制策略是具有可行性的。
5 结论
在PMSM 运行时,由于逆变器的非线性因素导致的电流谐波使得电机的损耗增大,影响了控制系统的稳定性。本文介绍了目前基于控制角度的一些谐波抑制策略,阐述了基波提取器的频率选择原理,通过改变正序基波提取器的角速度,提出了基于正、负序谐波提取器与电压补偿策略的永磁同步电机谐波抑制策略,通过正、负序谐波提取器来提取5,7 次谐波的交流分量,将提取的谐波量作为补偿量输入到电流环PI 控制器的输出电压中,实现谐波抑制的目的。较于传统谐波补偿方法,本文具有谐波补偿结构简单,计算量少,响应速度较快的优点。仿真结果验证了该算法的可行性,即该算法可以实现永磁同步电机的电流谐波抑制。

