开关磁阻电动机小样本磁链特性精确建模方法*

李存贺 赵 博 刘 剑 鲁炳林

(山东理工大学电气与电子工程学院 淄博 255000)

1 引言

开关磁阻电动机(Switched reluctance motor,SRM)因其结构简单、起动转矩大、调速范围宽、可靠性和效率高等优点，在油田抽油机、风力发电、电动汽车等领域有着广阔的应用前景[1-3]。建立精确的数学模型对SRM 性能评估和实施先进控制策略至关重要[4-5]。然而，SRM 自身的双凸极结构以及磁饱和特性导致很难通过常规电磁和物理特性推导获得其精确的非线性数学模型。

基于样机电磁特性数据，采用函数解析式进行非线性拟合[6-11]、神经网络或模糊系统逼近[12-16]的方法建立SRM 模型，是现在SRM 非线性建模的常用方法。文献[6]提出一种SRM 非线性磁链解析模型，采用指数形式表征电动机磁链与相电流和转子位置间的非线性关系。文献[7]对该模型进行了改进，引入增量电感项并将饱和磁链值取为转子位置的函数，使得该解析模型参数具有了一定的物理意义。文献[8]采用多项式函数对磁链随转子位置的变化特性进行分段建模，并将其应用于SRM 快速计算机辅助设计(Computer aided design，CAD)软件中。文献[9]采用傅里叶级数建立SRM 磁链模型，并通过反正切函数拟合磁链和电流之间的变化关系。文献[10]进一步通过两个嵌套的二阶傅里叶级数构造SRM磁链解析模型，并取得了较好的拟合效果。文献[11]基于电动机等效磁路法建立了考虑互感耦合的SRM非线性解析模型。然而，函数解析法的精度过度依赖于函数解析式的形式和函数解析式系数的拟合精度。

神经网络和模糊系统均具有通过学习逼近任意非线性映射的能力，非常适用于建立SRM 非线性模型。文献[12]将反向传播(Back propagation,BP)神经网络引入SRM 建模，网络采用双隐层结构，隐层神经元数均为8，输入为磁链和转子位置，输出为相电流，采用标准BP 学习算法。文献[13]采用基于LM 学习算法的BP 神经网络建立SRM 电流-磁链-位置模型，进一步提高了神经网络的训练速度，并且将隐层神经元数目减少为4 个。文献[14]采用小波神经网络(Wavelet neural network,WNN)建立了SRM 转矩模型，所建模型具有较强的泛化能力。文献[15]将采用Takagi-Sugeno 模糊形式的Pi-sigma 模糊神经网络用于建立SRM 磁链模型，并且通过结合变学习速率的网络学习算法，进一步提高了网络的收敛速度。文献[16]将自适应模糊推理系统(ANFIS)用于建立SRM 电感和转矩模型，选用反向传播法和最小二乘估计法组成的混合算法对ANFIS参数进行训练，取得了较好的建模精度。然而，上述建模方法均需要SRM 全周期磁链特性数据。

目前获取SRM 全周期电磁特性样本数据的方式主要为试验测量法即通过转子固定位置锁紧施加直流脉冲的方式间接求解电动机磁链曲线[17-18]。虽然上述磁链测试方法具有较高的测量精度，但是需要专门购买额外用来固定电动机转子位置的锁紧装置，增加了测试成本，并且对于已安装在工业现场连接有负载的SRM，很难通过该方法测量电动机磁链特性。文献[19]基于SRM 结构的对称特性，提出了利用转子的转矩平衡点测量电动机磁链特性，能够避免使用转子锁紧装置，并且可以提高测试效率。文献[20-21]进一步改进了该方法，将多相同时导通时的互感影响降到最低。然而，对于被广泛使用的三相SRM，基于转矩平衡位置的测量方法仅能获得四个特殊位置的小样本磁链特性，这极大地增加了精确建模的难度。

为了解决小样本磁链特性下的SRM 精确建模问题，本文提出一种基于模糊逻辑系统的磁链建模方法。该方法将模糊逻辑系统用于建立SRM 磁链模型，主要包括模糊空间划分、模糊规则提取和磁链求解三个步骤。所提出模糊建模方法将电动机先验知识用于模糊空间划分，并从样本数据中自动提取模糊规则，能够很好地将电动机先验知识与实测量数据相结合。相比传统神经网络建模方法，所提出方法大大提高了小样本数据下SRM 磁链建模精度。此外，在Matlab/Simulink 软件中进一步建立了SRM 驱动系统仿真模型，不同工作模式下的动态仿真和试验波形均具有很好的一致性，验证了所提出建模方法的有效性。

2 SRM 小样本磁链特性测量

根据电路基本定律，SRM 相绕组的电压平衡方程式为[22]

式中，u为相绕组两端电压，R为相绕组等效电阻，i为通过相绕组的电流，ψ为相绕组磁链。

由式(1)可以解出磁链表达式

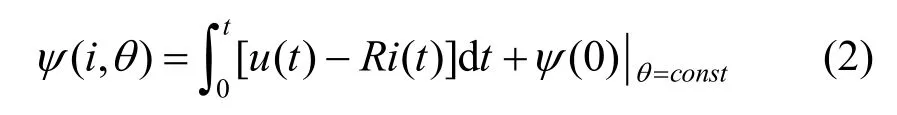
式中，ψ(0)是磁链初始值。由于SRM 内部无永磁体，故可认为ψ(0)=0。

对式(2)进行欧拉离散化可以得到

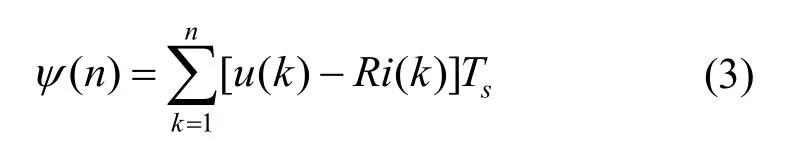
式中，n是采样点个数，Ts是采样周期。

从式(3)可以看出，只需要在转子稳定在某位置时，记录电流上升或下降过程中的电压和电流值，然后代入式(3)即可求得该位置下磁链随电流的变化特性。由于SRM 运行遵循“最小磁阻原理”，在给单相或多相定子绕组通电后，SRM 自身结构的对称性使得转子在一些特殊位置受力平衡，此时转子上合转矩为零，可以保持静止[20]。我们把这些受力平衡的特殊位置统一称为SRM 的转矩平衡位置。对于m相SRM，共有m+1 个转矩平衡位置。以三相12/8 极SRM 为例，其四个转矩平衡位置如图1 所示。

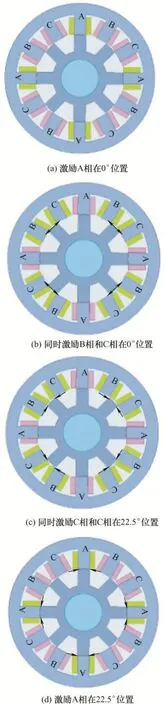
图1 SRM 转子转矩平衡位置处受力示意图

考虑到三相12/8 极SRM 结构的对称性，各相经过15°相移后可以获得相同磁链特性。本文中所有转子位置均相对于A 相，故测量得到的四条磁链曲线满足如下关系

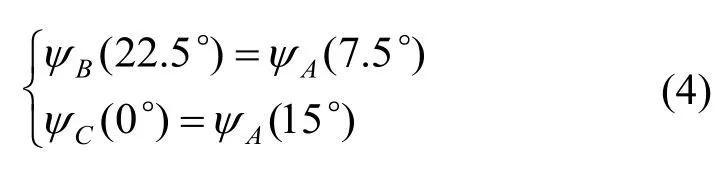
由式(4)可知，在A 相22.5°和0°位置，通过对不同绕组施加激励，可以获得A 相在0°、7.5°、15°、22.5°四个特殊位置处的小样本磁链特性。

搭建试验平台，对SRM 磁链特性进行测量，本文试验用样机为三相12/8 极SRM，额定功率1.5 kW，定子绕组电阻0.9 Ω。试验测量平台原理图如图2 所示。在测试过程中，通过激励不同的定子相绕组，即可以将转子吸引到这些特殊位置；在这些特殊位置，分别对不同相施加直流脉冲电压，记录相应的相电流和相电压数据，代入磁链计算公式(3)即可获得四个转矩平衡位置的磁链特性，如图3 所示。值得注意的是，在转矩平衡位置处测量磁链时，存在多相被同时激励的情形，为了最小化多相同时导通带来的互感对测量精度的影响，本文采用短磁路励磁方式NSNSNSNSNSNS[21]。

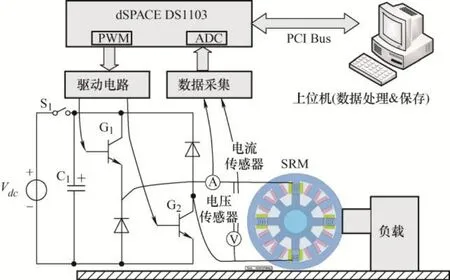
图2 SRM 磁链特性测试平台原理图

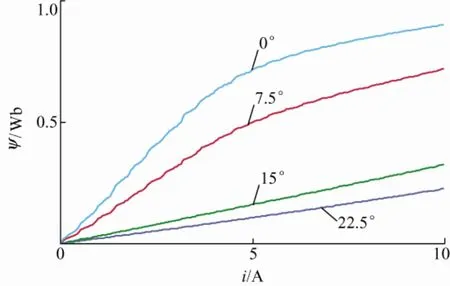
图3 转子转矩平衡位置处磁链特性曲线

图4 给出了相同位置处转矩平衡法和传统转子位置锁紧法测量磁链曲线的对比结果。从图4 可以看出，两种方法的测量结果基本一致，验证了基于转矩平衡方法测量四个特殊位置磁链值的有效性。

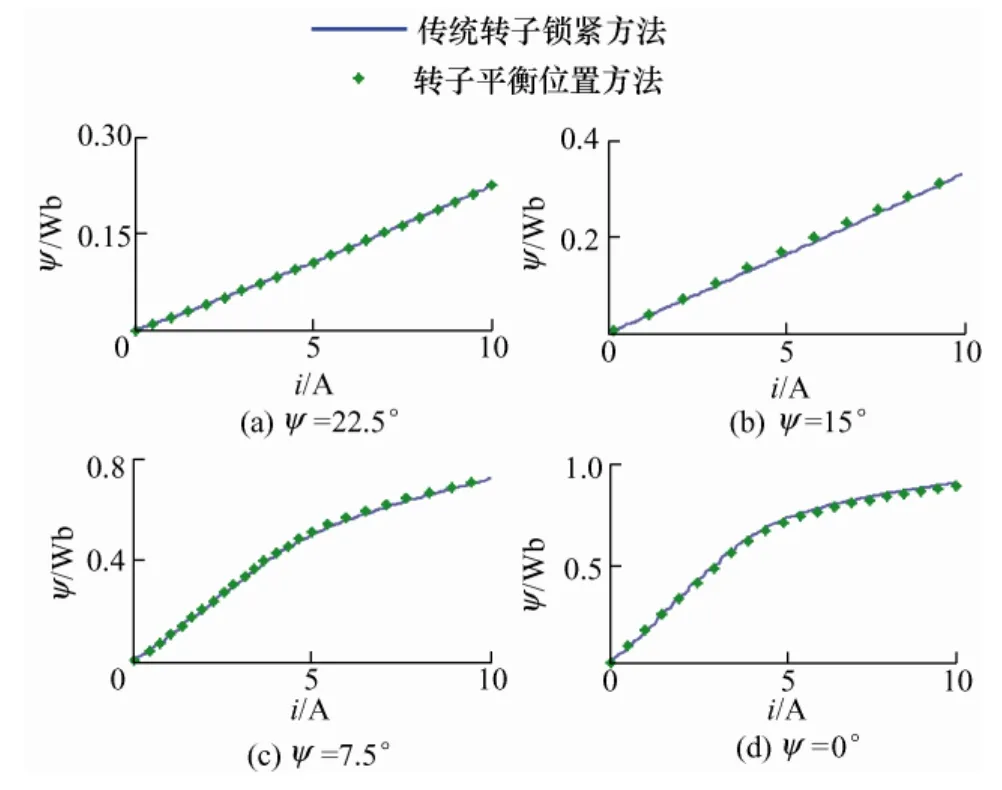
图4 转矩平衡法与传统转子锁紧法测量结果对比

3 基于模糊逻辑系统的磁链建模

模糊逻辑系统(Fuzzy logic system,FLS)具有良好的非线性映射能力，可以以任意精度逼近紧集上的任意非线性连续函数[23-25]。基于规则的模糊推理系统能够处理不确定、模糊的语言概念，而且模糊规则可以从样本数据中自动提取，非常适合用于解决复杂非线性对象的建模和控制问题[26]。本文结合SRM 磁链建模的实际需求，将样机的先验知识用于FLS 隶属度函数划分，并从测量获得的小样本磁链特性数据中自动提取模糊规则，进而完成小样本磁链特性下的SRM 精确建模。所提出建模方法的结构框图如图5 所示。

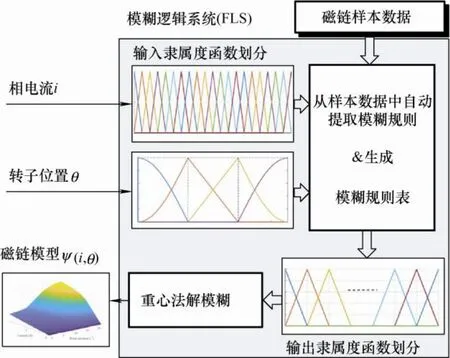
图5 SRM 模糊逻辑系统结构框图

3.1 模糊空间划分

对相电流而言，通过试验测量可以获得足够的磁链随电流变化的样本数据。综合考虑模型复杂度和精度，采用三角形隶属度函数对相电流进行模糊集划分，共划分为21 个区间，如图6 所示。

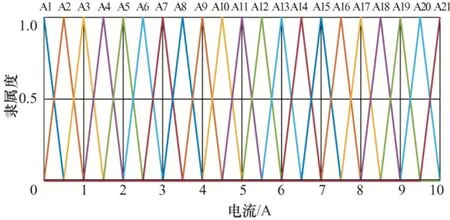
图6 模糊逻辑系统输入划分(电流)

图6 中，第j个电流模糊集Aj的隶属度函数可描述为

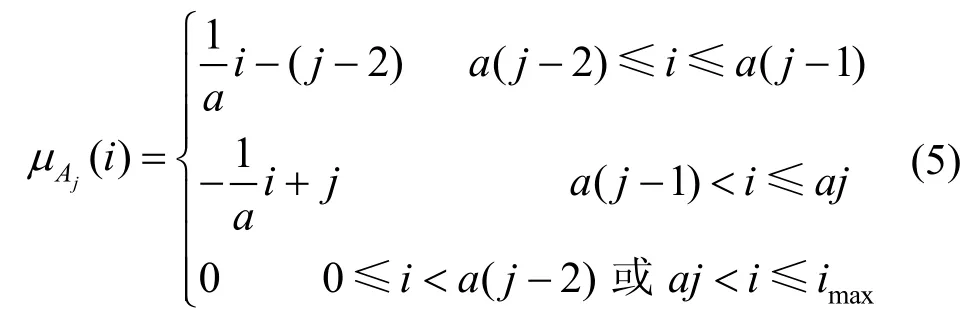
式中，imax为电流最大值，a=imax/20 为电流隶属度函数的步长。

对转子位置而言，基于转矩平衡法仅能测量得到四个特殊位置的磁链信息。有限位置的磁链数据对转子位置的隶属度函数选取和模糊集划分带来了难度。为了解决这个问题，将SRM 的先验知识引入转子位置的隶属度函数选取和模糊集划分。

对于任意给定的SRM 样机，磁链-位置(ψ-θ)特性的数值虽然存在差异，但大致的变化趋势是非常相近的。图7 给出了在特定电流下，磁链随转子位置的变化曲线。

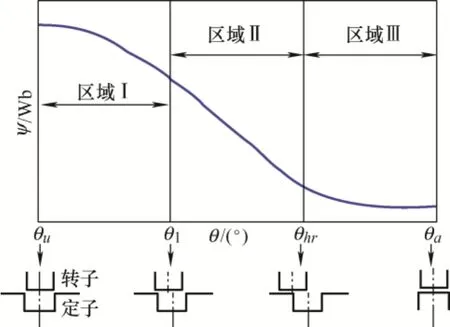
图7 磁链随转子位置变化特性

如图7 所示，磁链随转子位置变化曲线可以划分为三个区域，分别是区域I[θu,θ1)，区域II [θ1,θhr)和区域III[θhr,θa]。其中，θu是定转子凸极完全未对齐位置，θ1是转子极前沿和定子极前沿对齐位置，θhr是转子极中心线和定子极前沿对齐位置，θa是定转子凸极完全对齐位置。从图7 可以看出，磁链随转子位置的变化在区域II 可近似为线性关系，在区域I 和III 可近似为余弦关系。对于SRM，位置θ1和θhr可计算如下

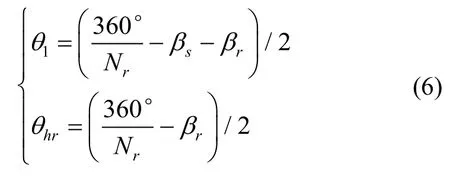
式中，βs和β r分别为定子和转子的极弧宽度，满足如下关系[21]

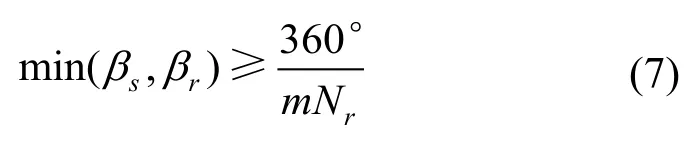
式中，m和Nr分别代表电动机定子相数和转子极数。对于三相12/8 极SRM 样机，m=3，Nr=8，故将式(7)代入式(6)，可得

综合上述分析，可将磁链-位置特性在位置区间[7.5°,15]° 上近似为线性关系，采用线性隶属度函数划分；在区间[0°,7.5]° 和[15°,22.5]° 上近似为余弦特性，采用余弦隶属度函数划分。对转子位置的模糊集划分如图8 所示。图8 中转子位置模糊集B1和B2的隶属度函数可分别描述为

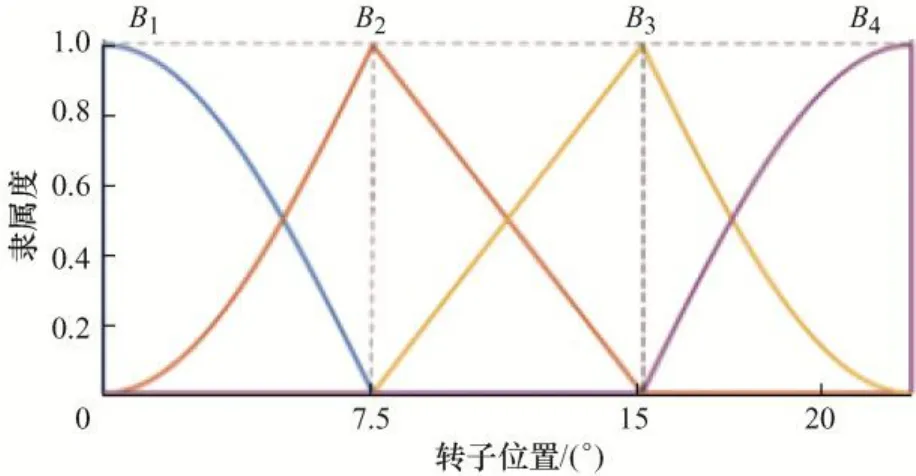
图8 模糊逻辑系统输入划分(转子位置)

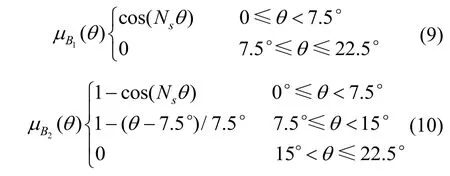
模糊集B3和B4分别与B2和B1关于中间位置对称，其成员函数不再赘述。

为了实现磁链特性的精确求解，对磁链可以采用更加精细的模糊划分。如图9 所示，本文利用三角形隶属度函数将磁链划分为201 个区域。图9 中第l个磁链模糊集Cl的隶属度函数可描述为

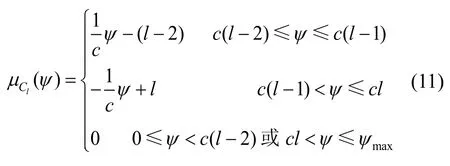
式中，ψmax为磁链最大值；c=ψmax/200为磁链隶属度函数的步长。

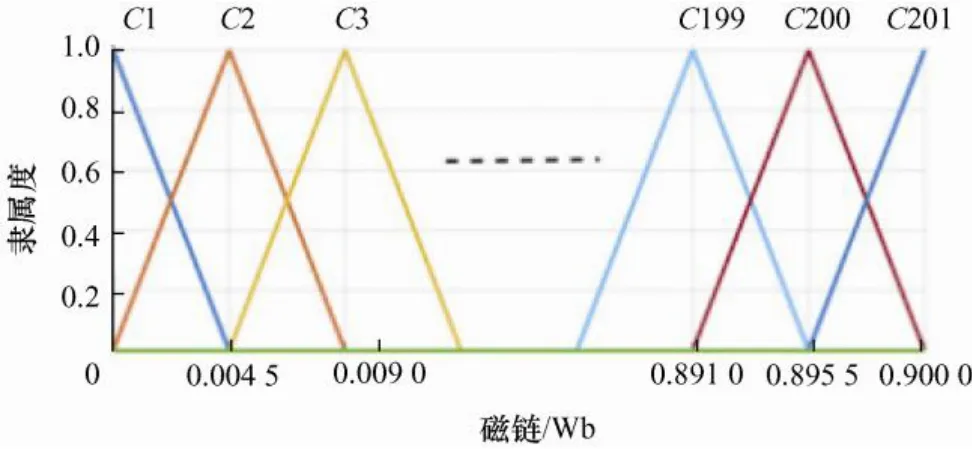
图9 模糊逻辑系统输出划分(磁链)

3.2 模糊规则提取

通常来说，当模糊集合数量较少时，模糊规则可由专家经验提供，而当模糊集合数量较多时使得专家经验很难提供相应的模糊规则。为了解决这个问题，本文采用基于系统的输入输出数据设计模糊推理系统的方法，从样本数据中自动提取模糊规则，克服了专家知识难以表达复杂系统的局限性。

模糊规则由前件和后件组成，可表述为：“Ifx1isAjandx2isBkthenyisCl”。针对SRM 磁链模糊逻辑模型，其每个输入输出数据对(i,θ;)ψ对应的模糊规则可以被描述为“R(s):Ifi(s)isandisthenψ( s)is”。对每个样本数据，均选择所对应的最大隶属度函数值，其相应的模糊集可分别计算如下

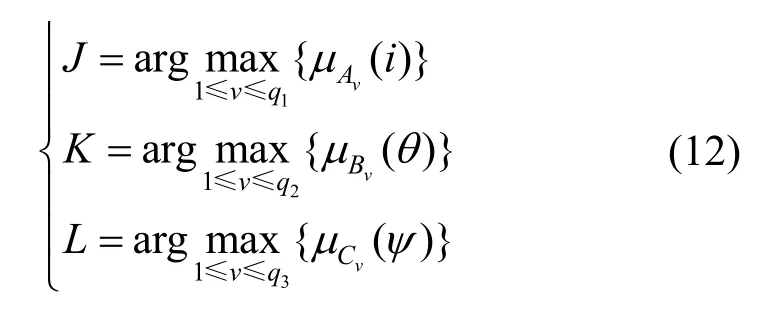
式中，q1、q2、q3分别为前件i,θ与后件ψ的模糊集数量。根据前面的模糊集划分，q1=21，q2=4，q3=201。所提取模糊规则R(s)的置信度D(R(s))可以计算如下

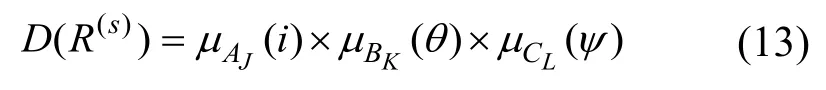
需要注意的是，部分样本数据具有相同的模糊前件，不同的模糊后件，即会产生相冲突的模糊规则，解决方法为选取最大置信度的规则作为最佳模糊规则[27]。基于测量得到的特殊位置磁链样本数据，完成模糊规则提取，如表1 所示。

表1 从样本数据中自动提取出的模糊规则库

以表1 中第3 行第2 列为例，其规则可以被描述为“If phase currentiis A3and rotor positionθisB2，then flux-linkageψisC8”。

3.3 磁链特性建模

解模糊是模糊化的逆过程，能够把模糊推理得到的模糊集转化为精确量。目前常用的解模糊方法有最大隶属度法、中位数法和重心法等多种方法。其中，重心法是取隶属度函数曲线与横坐标围成面积的重心，作为模糊推理的最终输出值，相比其他方法具有更平滑的输出推理控制，因此选用重心法对磁链进行求解。采用重心法SRM 任意电流和位置下的磁链输出可以计算如下

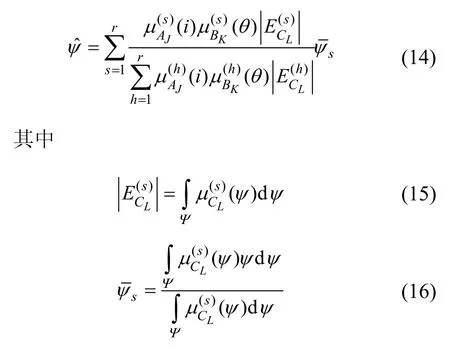
根据所提出的模糊逻辑系统建模方法计算得到SRM 全周期磁链值，如图10a 中点线所示。为了验证所提出方法的建模精度，将其与传统转子锁紧法测量磁链值(如图10a 实线所示)进行对比，对比结果显示两者具有较好的一致性。

图10b 进一步给出了相同磁链样本数据下采用BP 神经网络方法[13]的建模结果。BP 神经网络采用LM 学习算法，网络隐层数为1，隐层节点数为10，最大迭代次数为1 000，最小误差为0.000 5。从图10b 中可以看到BP 神经网络建模结果与转子锁紧法测量结果之间具有较大误差，无法实现小样本数据下磁链特性的精确建模。

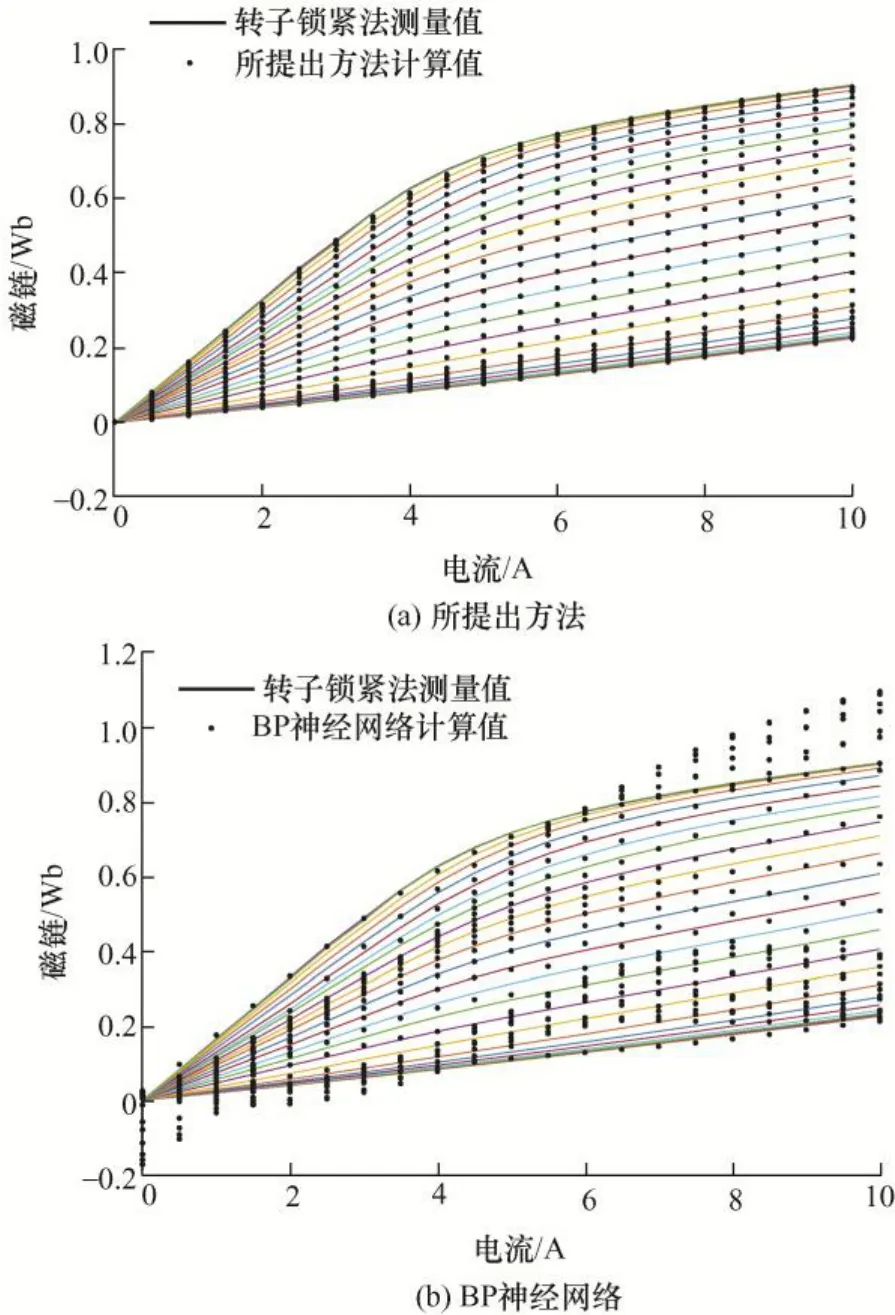
图10 磁链建模结果对比

为了定量分析所提出方法的建模精度，绘制磁链计算值与测量值的三维误差曲面和均方值误差(RMSE)曲线，如图11 所示。从图11 中可以看到，所提出方法和BP 神经网络方法最大误差值分别为0.028 Wb 和0.34 Wb，最大均方值误差分别为0.019和0.15。此外，从均方值误差曲线可以看出BP 神经网络方法除在有样本数据的四个特殊位置处RMSE 值较小外，在其余位置处RMSE 值均较大，而所提出方法在整个位置区间RMSE 值均小于0.02。以上对比结果说明所提出建模方法具有较高的建模精度，完成了SRM 磁链特性的精确建模。

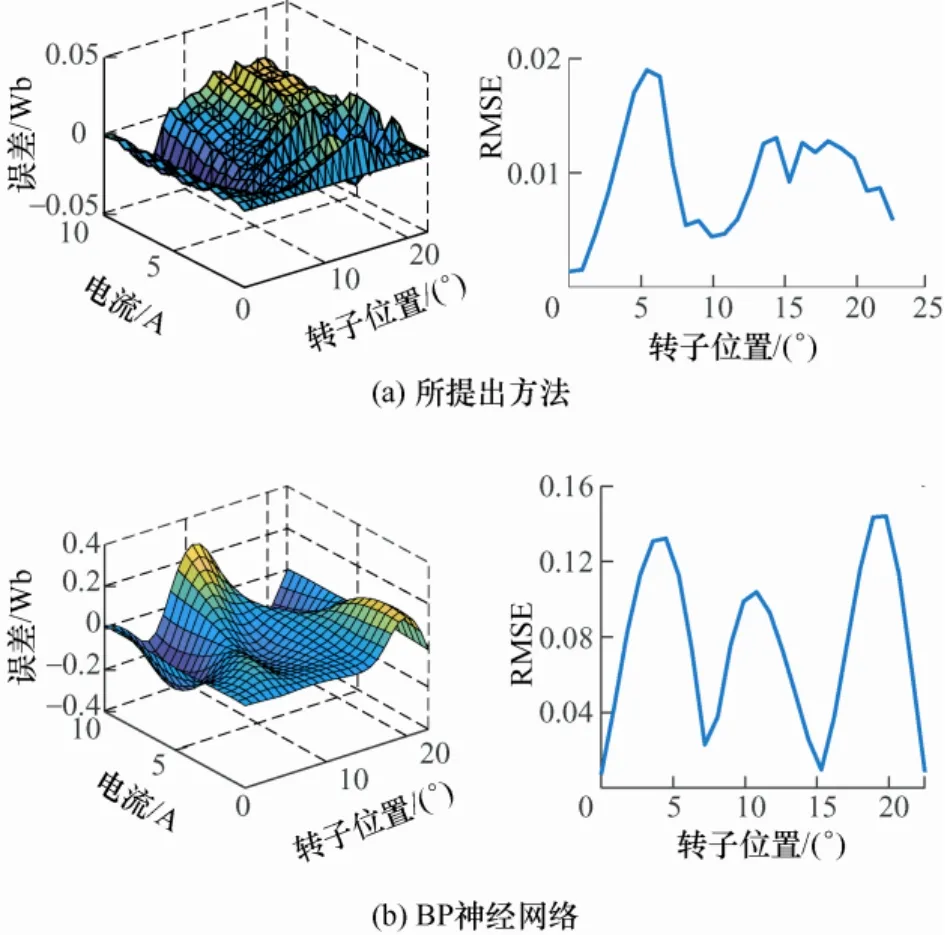
图11 建模误差对比

4 动态仿真与试验

为了模拟实际SRM 驱动系统运行特性，基于求解的磁链和转矩特性，在Matlab/Simulink 软件中建立了SRM 驱动系统动态仿真模型，对不同运行模式下的SRM 进行动态仿真，并和试验结果进行对比分析。SRM 驱动系统动态仿真模型和电动机本体仿真模型，如图12 所示。

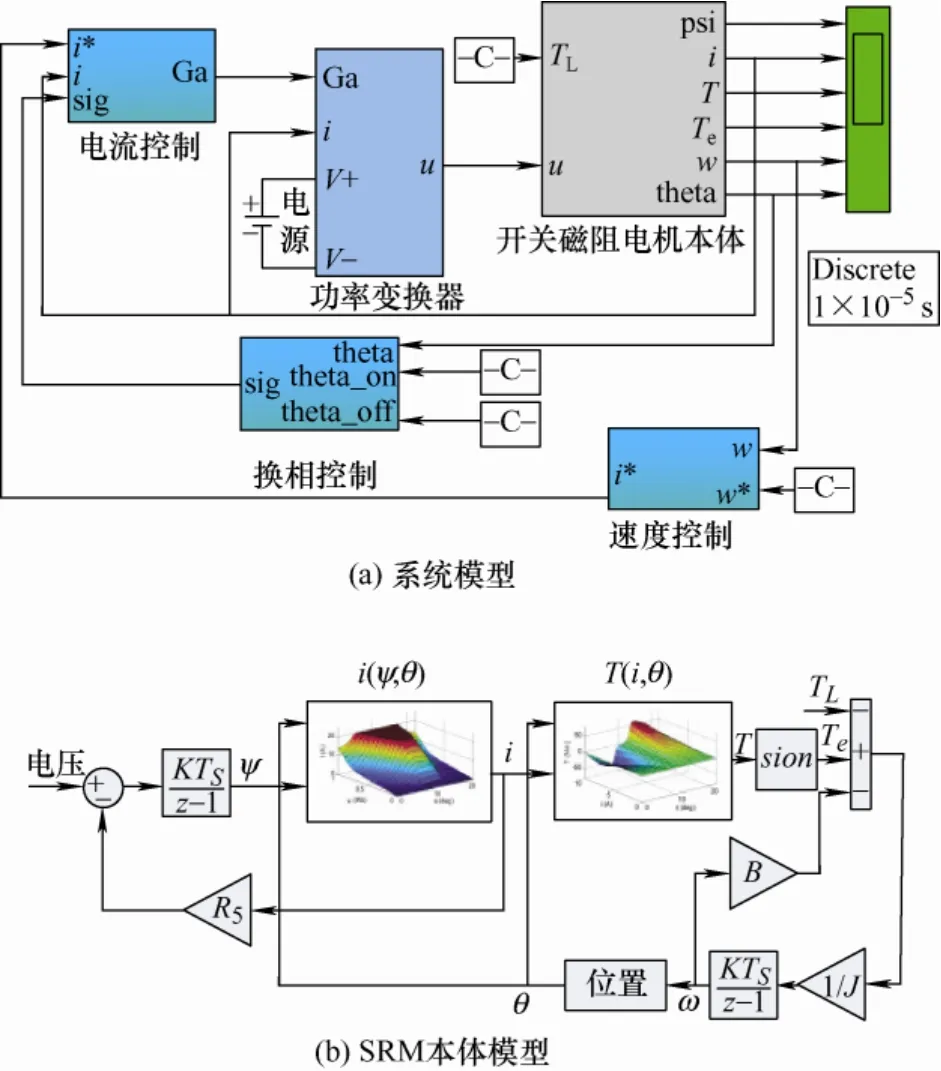
图12 SRM 仿真模型

图12 中电流-磁链-位置特性i(ψ,)θ由磁链-电流-位置特性ψ(i,)θ经反向插值得到，转矩-电流-位置特性T(i,)θ由磁链特性计算得到，即

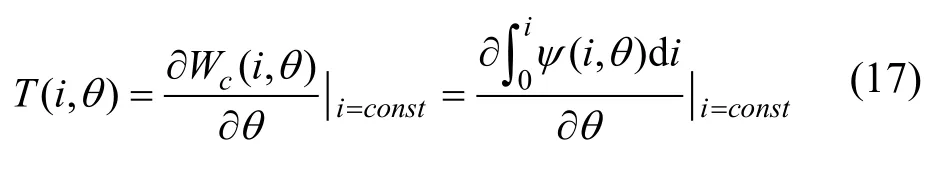
式中，Wc为SRM 磁共能。

SRM 动态仿真模型采用转速-电流双闭环控制策略，速度环和电流环的采样周期分别设定为1 kHz和10 kHz。外环转速控制器采用比例-积分(PI)控制，控制器参数为：kp=1，ki=0.2。内环电流控制分别采用电流斩波控制(CCC)和脉宽调制(PWM)两种运行模式。

为验证SRM 驱动系统仿真模型的精度，搭建SRM 驱动系统试验平台，在相同条件下进行试验验证和分析，整个试验系统如图13 所示。试验样机为1.5 kW 三相12/8 极SRM，样机参数如表2 所示。

图13 SRM 试验平台

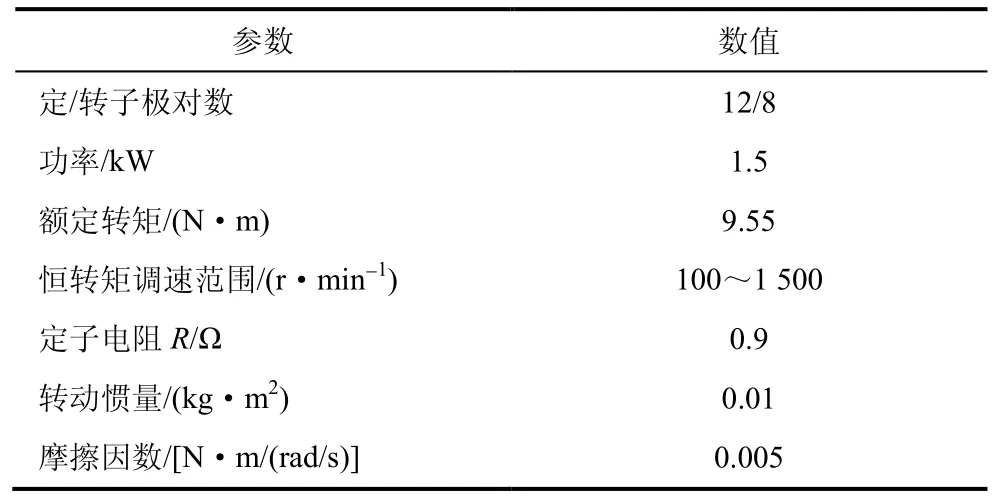
表2 试验样机参数

图14 给出了SRM 工作在参考转速400 r/min，CCC 模式下的电动机实际运行波形和仿真波形对比。图14a 和图14b 分别为负载转矩2.8 N·m 和负载转矩5.6 N·m 时的仿真和试验波形对比。从图14 中可以看出两种不同负载下的仿真波形和试验波形均具有较好的吻合度。

图15 给出了SRM 工作在参考转速400 r/min，PWM 模式下的仿真及试验电流波形。图15a 和图15b分别为负载转矩2.8 N·m 和负载转矩5.6 N·m 时的仿真与试验电流波形对比。从图15 中可以看出，两种不同负载下的仿真和试验电流波形均具有较好的一致性。此外，从图15 中可以看到，电流仿真波形在下降段与实际电流波形误差较上升阶段更大，这是因为在磁链特性测量过程中，仅截取了相电流上升阶段的数据计算磁链，忽略了磁滞效应影响。后续为了进一步提高仿真模型精度，应该尝试建立考虑磁滞效应的模型。

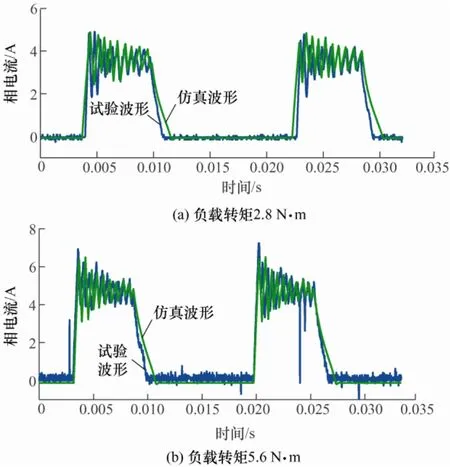
图14 CCC 模式下相电流试验和仿真波形

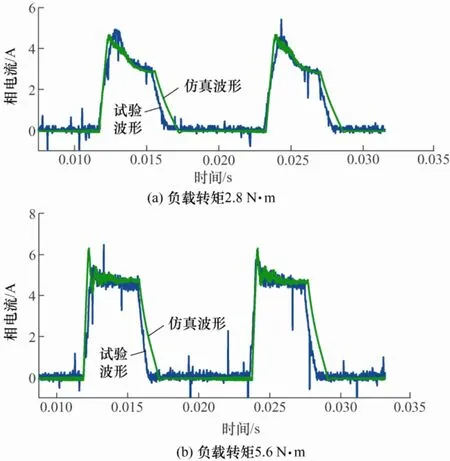
图15 PWM 模式下相电流试验和仿真波形

试验结果说明了所建立SRM 驱动系统仿真模型具有较高精度，可以用于SRM 动态和稳态性能分析以及高性能控制器设计。

5 结论

本文提出了一种适用于SRM 小样本磁链特性的模糊逻辑系统精确建模方法。该方法可以把SRM极对数和磁链随转子位置变化趋势等电动机先验知识用于模糊隶属度函数的选取和模糊集划分，并且能够基于样本数据自动创建模糊规则库，实现了SRM 小样本磁链特性下的精确建模。与BP 神经网络模型的对比结果表明，所提出模型极大地提高了小样本数据下SRM 磁链的建模精度。基于所建磁链模型，进一步在Matlab/Simulink 中搭建了SRM驱动系统仿真模型，仿真和试验对比结果显示，不同运行模式下的SRM 驱动系统仿真与试验波形均相互吻合，说明所建立的SRM 驱动系统仿真模型具有较高精度，可以为SRM 运行特性分析与先进算法验证提供有力支撑。