基于粒子群算法的最优照度均匀度LED阵列设计

董铂龙

基于粒子群算法的最优照度均匀度LED阵列设计

董铂龙

（四川大学机械工程学院，四川 成都 610000）

通过设计LED阵列排布，使得接收平面上的照度均匀度最大，这对LED照明系统具有十分重要的意义。不同于传统的数值计算的方法，此次采用粒子群算法来进行LED阵列排布的优化，使其在接收平面上的照度均匀度最大。首先推导了线性LED阵列的照度分布函数，并通过对比度来对照度分布函数的均匀度进行评价。然后采用粒子群算法求取均匀度最大时的LED排布，并同数值计算得到的结果进行比较，验证粒子群算法的可行性。

粒子群算法；LED阵列；最优照度均匀度；对比度

1 引言

LED阵列是将多个LED按某种规律的排列方式进行排列组合而成的光源。这种光源常用于单一LED光源无法提供所需光强的场合，如室内室外照明，或者对光照区域、光照角度等有特殊要求的场合，如摄影光源、机器视觉光源等。

而在LED阵列的应用过程中，很多情况下都对LED阵列在照射表面上的照度均匀度有较高的要求。例如在机器视觉过程中，可以采用矩形LED阵列，LED阵列的照度均匀度会直接影响到相机拍摄的图片的质量[1]。又例如，在尘埃浓度测试中，LED阵列光源的光照度均匀性会直接影响尘埃浓度的检测精度[2]。此外，在针孔检测、生活照明、光照加热等领域也需要通过LED阵列实现较高的光照度的均匀度。

LED阵列的光照均匀度与单个LED的光照强度曲线、LED之间的排列方式、LED的电流大小、照射平面到发光平面之间的距离等有关。因此LED阵列的光照均匀度最优设计实际上就是一个多目标优化问题。

通常来说，LED阵列中的所有的LED的型号相同，因此不同LED的光照强度曲线也近似相同。此外，照射平面到发光平面之间的距离通常来说是在进行光源照度均匀性设计之前就已经根据光路设计和机械设计等确定。因此，光照均匀度设计问题实际上就是在给定单个LED的光照强度曲线以及照射平面到发光平面之间的距离的情况下，如何设计不同LED的排列方式和电流，从而实现LED阵列的光照均匀度最优的多目标优化问题。

对于这种多目标优化问题，可以采用粒子群算法来进行求解。本文即采用粒子群算法，求解出线性LED中使得光照均匀度最优的排列参数。

2 LED阵列的光照度模型

2.1 LED阵列照度分布建模

根据朗伯定律，普通的发光二极管近似是一个非理想朗伯体，其光强分布为发光角余弦多次方的函数[3]，即在空间中，与光轴夹角为处的光强为：

（）=0cosm（1）

式（1）中：0为光轴处的光强大小；为余弦的次方值。

值通常由LED的生产厂商给出，也可以通过半光强角1/2（该角度的光强为光轴处光强一半）计算得到：

此外，假设光源为点光源，则距离发光光源为处的光照强度为[4]：

假设第个光源坐标为（，，0），距离为的接收平面上的任意一点（，，）光强可以根据上式，进行球坐标到直角坐标变换后即可得到：

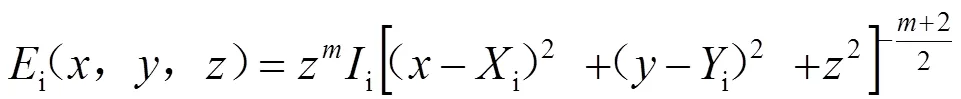
由于LED光为非相干光源，因此在个LED组成阵列的情况下，接收平面上的任意一点（，，）的照度等于各个LED在该点的照度的叠加。即：

式（5）中：i为第个LED的光轴光强，该值与LED的输入电流成正比，因此各个LED的i的比值即为各个LED的输入电流的比值，因此可以用i来代表LED的电流。

2.2 LED阵列照度均匀度评价指标

已知目标区域内的光照度，通过对比度的方法来表示目标区域内的光照度均匀度：

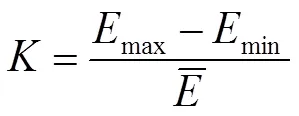
越小，则目标区域的光照越均匀；越大，则目标区域的光照越不均匀。

由此将光照强度公式和光照均匀度描述公式联立，构建了一个评价函数，将求取光照均匀度的问题转变成了求评价函数最小值的问题。评价函数为：

（1，1，1，…，i，i，i，…，n，n，n）=（7）

3 粒子群算法实现

3.1 粒子群算法简介

粒子群算法是一种基于迭代的优化方法，系统初始化为一组随机解，通过迭代寻优，粒子在解空间追随最优的粒子进行搜索。每次迭代中，粒子通过跟踪自身当前找到的最优解（个体极值）和整个种群当前找到的最优解（全局极值）来更新自己[5]。

在维空间内，由个粒子组成的种群=（1，2，…，n），每个粒子具有位置和速度（每次迭代的位置变化量）两种属性，即i=（i，i）。其中i、i均为维向量，i=（i1，i2，…，iD），i=（i1，i2，…，iD）。

根据粒子位置和评价函数，可以计算出该粒子的适应度，即：

i=（i）=（i1，i2，…，iD） （8）

因此可以得到整个种群中各个粒子的适应度为=（1，2，…，n）。

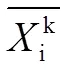
在每次迭代过程中，粒子首先根据自己的迭代前的速度、到个体极值的距离和到全局极值的距离，对粒子的速度进行更新，再根据当前速度以及迭代前的位置，得到迭代后的位置，从而实现粒子位置的不断迭代。即：

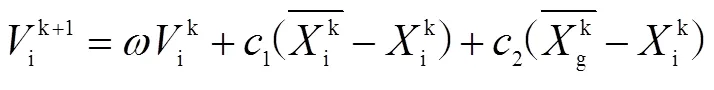
式（9）中：为惯性权重；1、2为加速因子，其取值在0～4之间。

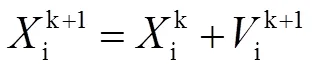
经过多次迭代后，取整个种群的最优解为最终结果。

3.2 粒子群算法设计

根据粒子群的实现方式，我们将LED的位置和电流大小作为粒子的位置属性，即：

=（1，1，1，…，i，i，i，…，

n，n，n） （11）

根据公式（7），将评价函数作为粒子适应度的计算公式。

然后通过图1所示的流程，进行光照均匀度的粒子群最优求解。

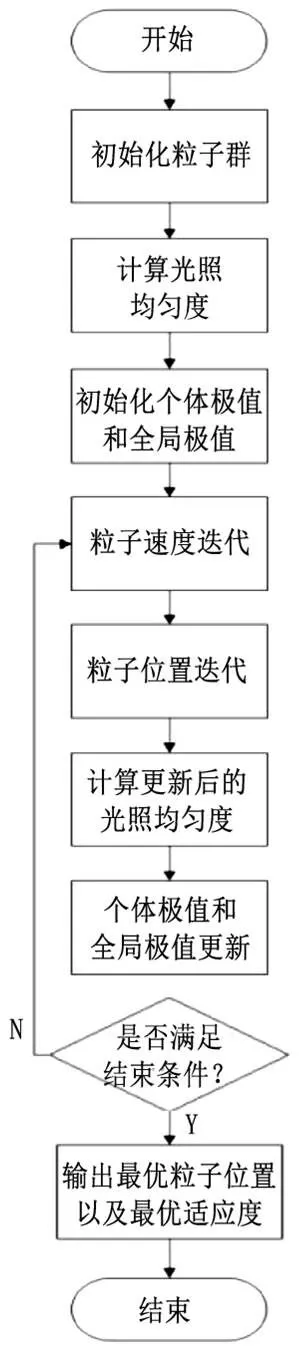
图1 粒子群算法流程图

初始化粒子群：在给定范围内，随机生成粒子种群的初始位置和初始速度。

计算光照均匀度：根据公式得到初始种群的光照函数并计算出光照均匀度作为个体适应度。

初始化个体极值和全局极值：记录初始种群的个体极值和全局极值。

粒子速度迭代：根据个体极值和全局极值，以及迭代前的速度，对粒子速度进行更新。

粒子位置迭代：根据迭代后的速度以及迭代前的位置，对粒子位置进行更新。

计算更新后的光照均匀度：根据公式得到迭代后的阵列的光照函数并计算出光照均匀度作为个体适应度。

个体极值和全局极值更新：比较和记录个体极值和全局极值。

是否满足结束条件：是否满足迭代次数要求或精度要求。

输出最优粒子位置以及最优粒子适应度。

4 仿真实验和结果分析

4.1 实验模型简介

以LED线性阵列排布为例，采用三种不同的方法来对相同排列方式的LED阵列进行光照均匀度最优排布设计，从而验证粒子群算法在进行LED最优光照均匀度排布求解时的可行性。

假设LED的排布方式为线性排布，且LED个数为奇数，其总数为2+1，相邻LED的距离为，发光面到接受面之间的距离为，建立的仿真模型如图2所示。

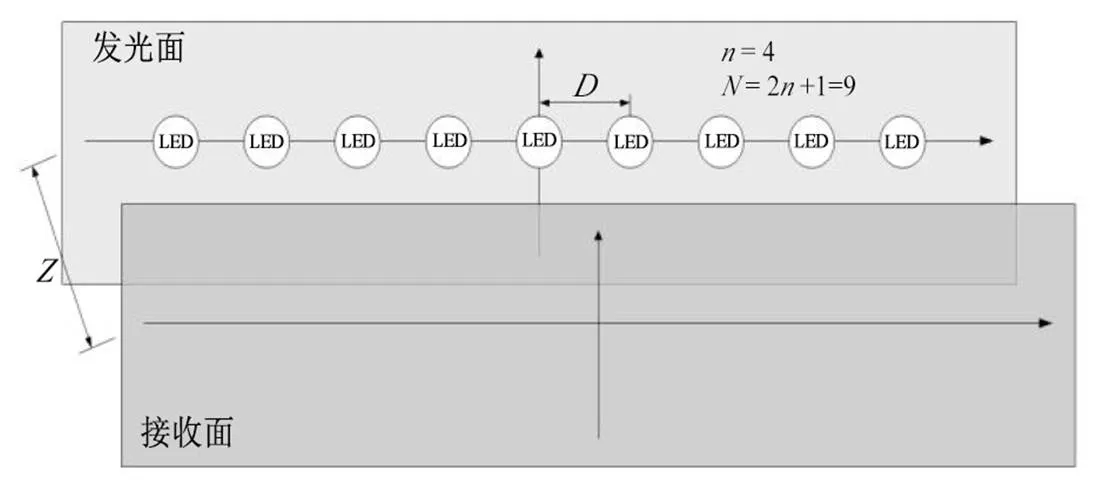
图2 仿真模型示意图

取LED的半光强角为11°，=25，则LED个数为51，发光面到接受面之间的距离=50，相邻LED的距离=20，LED的电流大小=1，则可以得到接收平面的光强分布如图3所示。

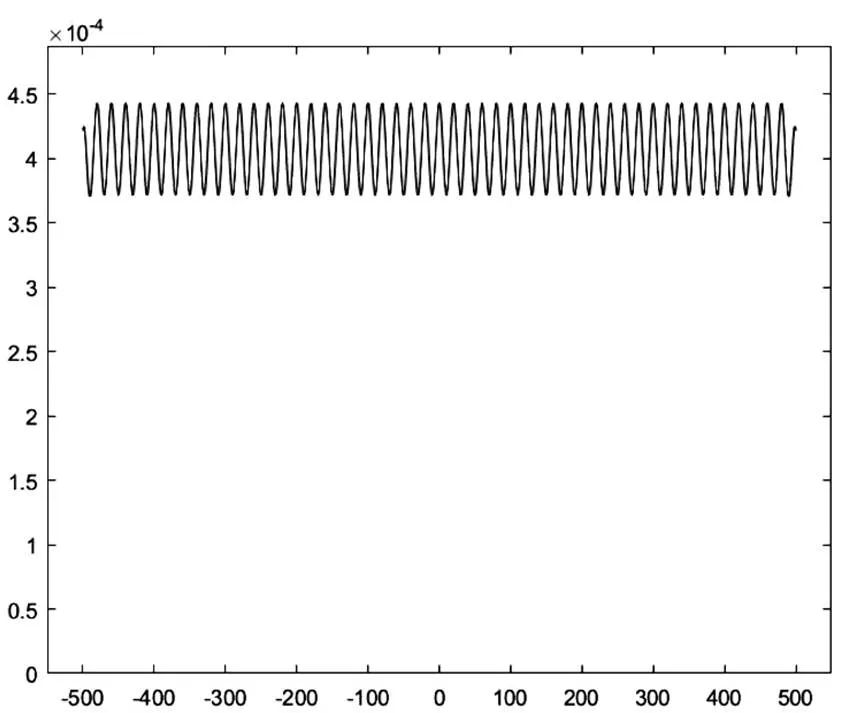
图3 D=20时接受面的照度分布

通过计算，此时光照均匀度=0.089 2。

4.2 数值计算方法求解

采用数值计算的方法，其他参数不变，只有改变时，且步长为0.005，光照均匀度评价系数随的变化曲线如图4所示。

图4 评价系数K随D的变化曲线

由图4可以看出，随着的不断增加，光照均匀度评价系数先减小，后增加。当=17.67时，最小，此时光照均匀度最大，=0.043 1。

此时的光照强度曲线如图5所示。

4.3 粒子群算法求解

采用粒子群算法求解，同样其他参数不变，能够实现最优光照均匀度的的大小。粒子群种群个数为15个，经过20次迭代后的收敛过程如图6、图7所示。

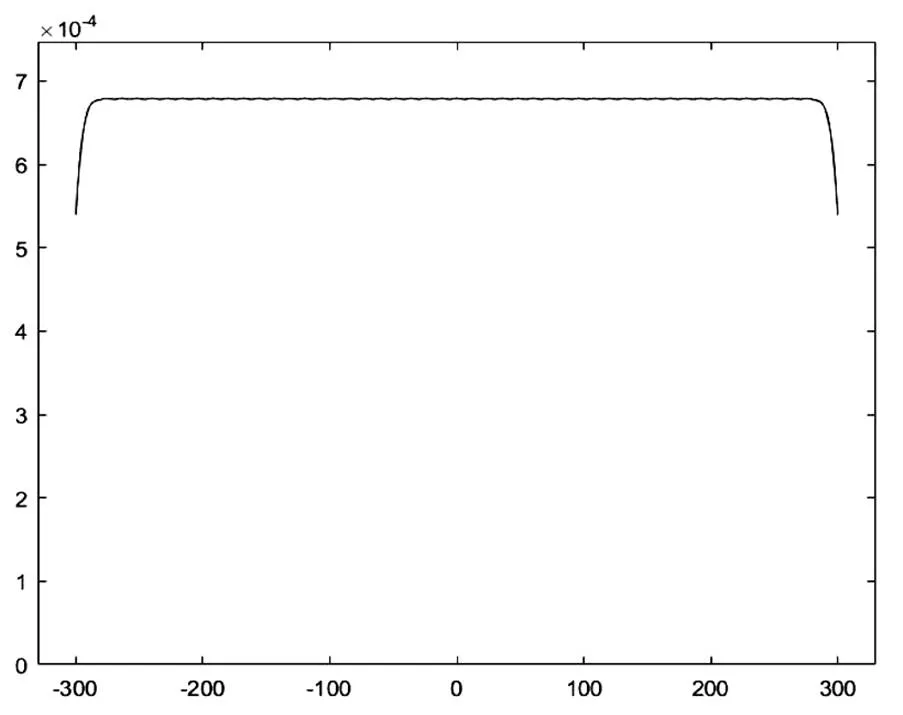
图5 D=17.67时接受面的照度分布

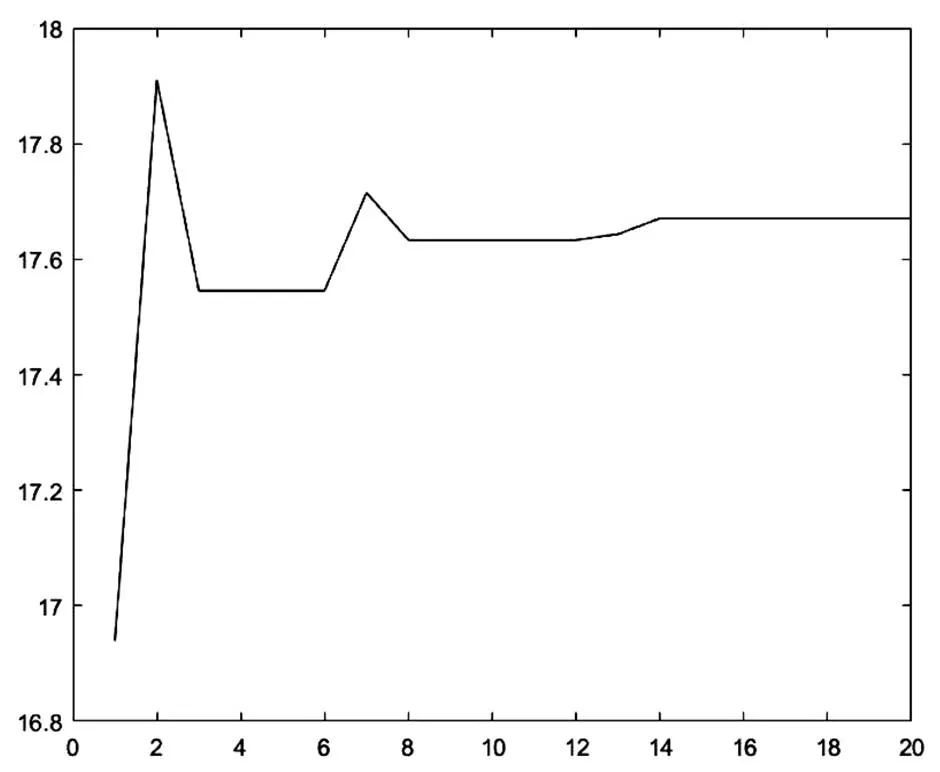
图6 位置收敛过程

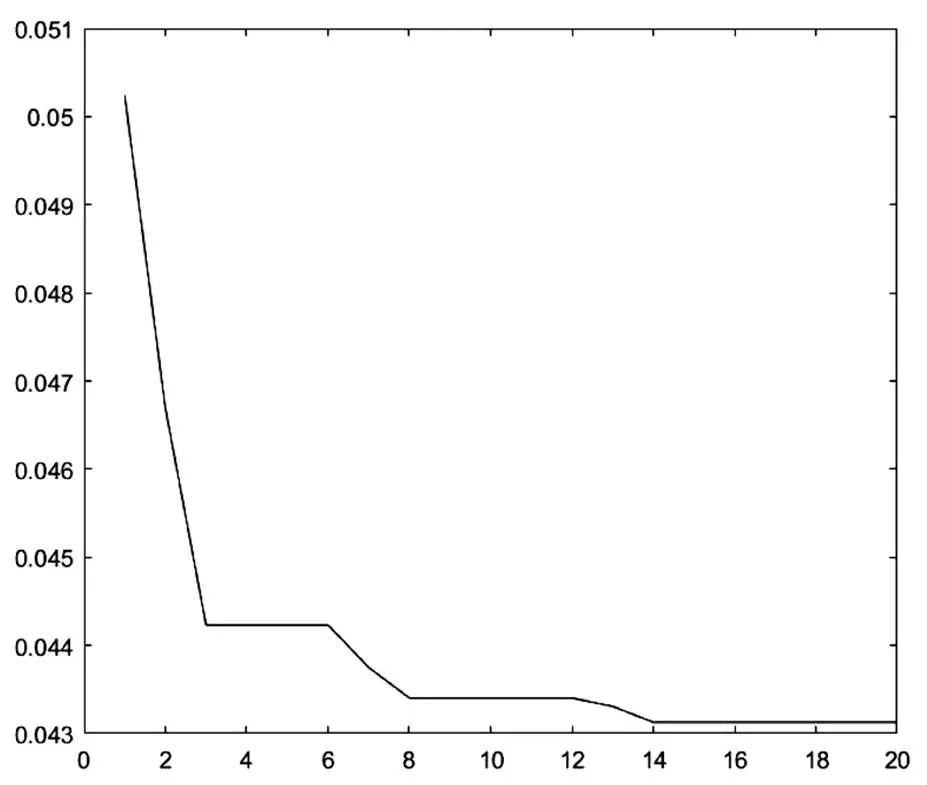
图7 适应度收敛过程

其最优结果为，当=17.670 8时，均匀度系数=0.043 129。

4.4 实验结果对比

通过对比4.2和4.3的结果可以看出，通过粒子群算法得到的光照均匀度的最优解pop=17.670 8，与枚举法得到的光照均匀度最优解num=17.67之间的误差为：

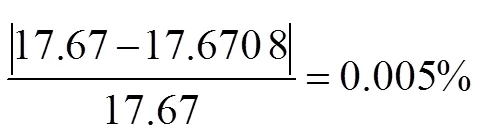
光照均匀度之间的误差为：

由此可见，基于粒子群算法的光照均匀度最优阵列设计与数值法得到的最优阵列设计之间误差很小。

而在较为复杂的情况，例如矩形排布、圆形排布等采用数值法时运算量巨大的情况下，可以通过采用粒子群算法来进行最优排布设计。

5 总结

本文首先对阵列LED的光照强度进行数学建模，将平面上的光照强度通过数学表达式进行计算，并提出通过指标来评价光照均匀度，然后通过粒子群算法求最优光照均匀度下的阵列LED排布，并通过实验仿真验证了粒子群算法得到的最优LED阵列排布和数值法得到的最优LED阵列排布之间的关系，为LED阵列均匀照明问题提供了一定的参考价值。

［1］ZHANG H L，PENG L，LUO Y K，et al.Rectangular illumination method using LED arrays for machine vision［J］. Applied optics，2020，59（11）：3518-3525.

［2］LI H S，SANG X Y.LED array light source illuminance distribution and photoelectric detection performance analysis in dust concentration testing system［J］.Sensors and actuators a physical，2018，271（1）：111-117.

［3］TAN J，YANG K，XIA M，et al.Analysis of uniform illumination system with imperfect Lambertian LEDs［J］. Optica applicata，2011，41（3）：507-517.

［4］郁道银，谈恒英.工程光学基础教程［M］.北京：机械工业出版社，2007.

［5］KENNEDY J，EBERHART R.Particle swarm optimization［C］//Icnn95-international conference on neural networks. IEEE，2002.

TM923.01

A

10.15913/j.cnki.kjycx.2021.08.007

2095－6835（2021）08－0022－03

董铂龙（1996—），男，硕士研究生在读，研究方向为测量与控制，研究内容为高速铝箔针孔检测。

〔编辑：王霞〕