基于自动车牌识别数据的混合交通流饱和流率实时估计

王殿海，郭佳林，蔡正义

(浙江大学，建筑工程学院，智能交通研究所，杭州310058)

0 引言

城市道路交叉口的交通流组织和控制，是城市交通研究中的重要课题。其中，饱和流率是计算交叉口通行能力、优化信号控制方案的关键基础参数。饱和流率的定义为：在连续绿灯时间内，某条进口道所能通过车辆的最大稳定流率[1]。饱和流率的大小受车辆构成类型，车道位置，排队位置及车辆间相互关系等影响。混合饱和流率是为计量城市道路上组成成分、动力特性、外形尺寸和行驶行为不同的交通流饱和流率而提出的指标。

针对混合饱和流率的测算已有大量研究。最经典的是美国通行能力手册[1](Highway Capacity Manual，HCM)提出的，在理想饱和车头时距的基础上乘以大车比例、车道宽度等影响因素的折减系数来计算饱和流率，各影响因素通过经验公式或者回归模型标定相关参数确定折减系数。目前，国内外关于饱和流率的研究均在HCM法的基础上对饱和流率影响因素进行分析并构建回归模型，如：NGUYEN H.D.[2]讨论以摩托车为主要交通构成的城市混合交通流饱和流率；SUSHMITHA R.[3]建立针对发展中国家无车道线交叉口的混合饱和流率回归分析模型；SAHAA.[4]针对HCM法无法考虑交通流构成的异质性问题，基于克里金法对影响混合交通流饱和流率的因素进行分析，并构建4种饱和流率模型。这类混合交通流饱和流率测算方法简洁有效，但有以下不足：第一，在现有技术条件下主要靠人工调查确定混合交通流构成比例并拟合相关参数，同时需要讨论不同环境条件带来的影响，费时费力。第二，采用静态调查方法标定参数，无法考虑混合交通流构成的时空异质性变化，使用时默认调查前后交通流构成比例不变，与实际不符。第三，由于目前信号控制系统并不能检测出车辆类型和混合交通流的车辆构成比例，故不能直接用于实时生成或优化交通控制信号方案。

部分学者假设某交通指标可以“等价”混合交通流的饱和流率特征，从而建模计算混合流率。例如，敖谷昌等[5]提出基于时间占有率分析的车辆换算系数。WANG D.H.[6]提出车道有效宽度的概念，针对城市道路专门建立自行车换算系数的模型，这种方法需要针对不同交通流单独建模分析，依赖其他交通指标进行评价。

近年来，部分研究采用数据驱动的方法，利用收集的车头时距数据，提取相应的统计学习特征，如排队位置、车型等，建立数据统计特征与混合饱和流率之间的关系。例如，LI L.[7]针对不同车头时距分布对宏观、微观交通流模型的影响进行分析。刘明君[8]通过对北京城市道路信号交叉口车头时距分析，建立针对混合交通流车头时距的SVM(Support Vector Machine)模型。严颖等[9]将车头时距分为饱和状态和非饱和状态，利用高斯混合分布模型识别车头时距对应的状态，提取饱和状态车头时距，但缺少对混合交通的建模讨论。这类方法不依赖假设，数据拟合精度高，但实际应用困难，需要不断进行模型的训练和预测。

综上所述，虽然在估计混合饱和流率问题上研究方法相对丰富，但停留在事后对数据分析处理上，或者没有考虑混合交通带来的耦合影响，不能用于实时交通信号控制。

随着城市大范围电子警察和卡口监控等基础设施的广泛布设应用，实时获取城市海量ALPR数据成为现实。本文提出利用数据实时估计信号交叉口混合交通流饱和流率的方法。首先，从ALPR数据中分信号周期提取车头时距数据，在当前车和后车车辆类型确定时车头时距满足同一正态分布的假设基础上，构建车头时距的高斯混合模型并应用EM 算法求解；其次，基于AIC 准则选取模型的最佳聚类数目，拟合数据得到高斯混合模型参数；最后，根据车头时距的高斯混合模型推算出混合交通流饱和流率。

1 数据的采集与处理

自动车牌识别数据是基于布设在交叉口停车线处的高清摄像机捕获的图像进行图像识别处理得到的，包含通过车辆的车牌信息、时间戳及车道信息。可以基于自动车牌识别数据的时间戳计算某车道上前后车的车头时距，提取车头时距的步骤如下。

Step 1 将第i车辆经过的时刻ti减去前车经过的时刻ti-1得到当前车辆的车头时距hi。

Step 2 根据当前信号灯的信号状态判定当前车辆在绿灯相位启动后的通过次序。

Step 3 以信号周期为单位提取各信号周期内该车道所有离散车头时距及其通过次序。

Step 4 选取高峰期饱和状态下某一绿灯相位启亮后的数据，根据HCM[1]饱和车头时距实测法的建议，以及文献[8]指出的当饱和释放超过30 s 时，饱和流率计算值会降低且不稳定，需要设置判断规则对获取的车头时距数据进行筛选，以获取饱和释放的车头时距。判断规则为：首先，选取第5 辆车为稳定车头时距的起点，第10 辆车作为稳定车头时距的终点。结合实际经验，前10 辆车车头时距极限情况下平均不超过3 s，在30 s 绿灯时间内，至少能通过10 辆车，则认为第5～10 辆车的饱和释放车头时距数据相对稳定。其次，该车道应处于饱和状态，则一个信号周期内释放的车辆数A满足

式中：gs为该信号口该周期内的有效绿灯时间，通过信号周期数据获得；h*为预估的混合饱和车头时距，根据经验预设，根据调查经验取h*=2.5 s。当时，认为该车道已处于饱和状态。

自动车牌识别数据采集如图1所示。

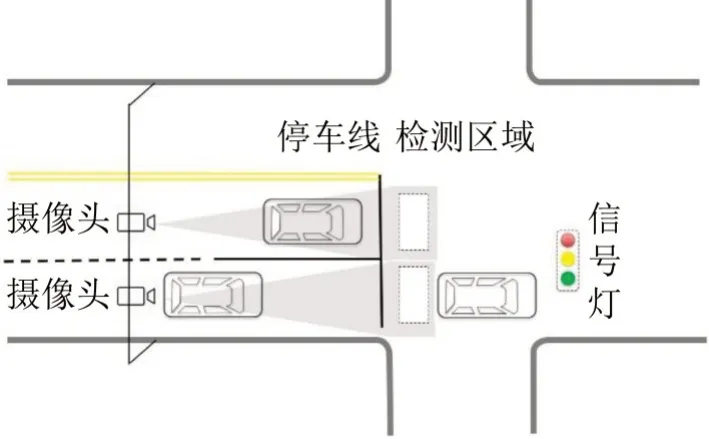
图1 自动车牌识别数据采集示意Fig.1 Operational principles of automatic license plate recognition system

2 模型的构建与求解

2.1 模型的构建

混合交通流的车头时距示意如图2所示，其中，Nαβ代表前车为第α种车，后车为第β种车时的车头时距。本文假设当同一车道前后车的车辆类型固定时，车头时距是满足同一分布的，即当前车为小汽车(car)，后车为公交车(bus)时，所有该类型的车头时距Ncb满足同一分布；前车为小汽车(car)，后车为小汽车(car)时，所有该类型的车头时距Ncc满足同一分布。

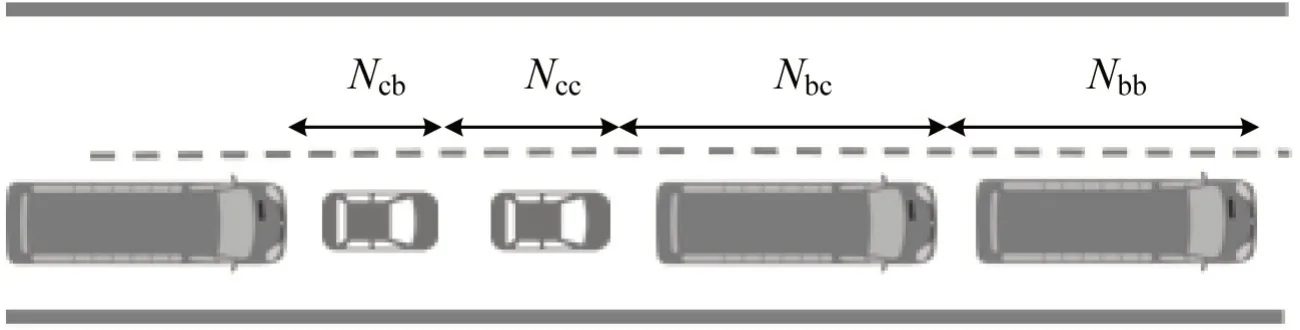
图2 混合交通流的车头时距示意Fig.2 Diagram of headway of mixed traffic flow

针对车头时距的分布，根据不同场景和交通流条件，可以建立不同的分布模型，如高斯分布、对数正态分布等[7]，在实际应用中可以对分布类型作假设检验，选取合适的模型。以常见的车头时距分布——高斯分布[10]为例，假设某前后车固定车型的车头时距数据满足分布N(μα,β,σ2α,β)，那么同类型前后车的车头时距满足同一高斯分布。在现实场景中，单从自动车牌识别数据无法判断通过车辆的类型，因此，无法提取同一类型的车头时距进行参数估计，此问题转化为：估计一个由若干类车头时距组成的高斯混合分布的参数。

假设车头时距h1,h2,…,hn满足类数为K0的混合高斯分布，表示为

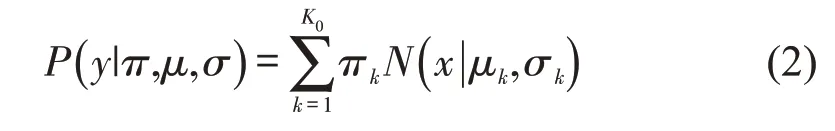
式中：(π,μ,σ)=(π1,π2,…,πk;μ1,μ2,…,μk;σ1,σ2,…,σk)，πk为混合系数，表示选择第k个高斯分布的概率，k=1,2,…,K0；N(x|μk,σk)为参数为μk,σk的高斯概率密度函数，表示第k类高斯函数；x,y分别为满足混合高斯分布和满足高斯分布的随机变量分布模型，即

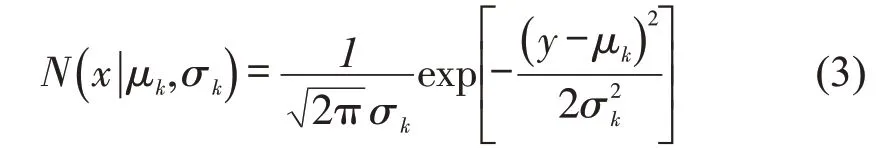
如果车头时距满足对数正态分布，则令y′=lny,将y′带入式(1)即可。

对于未知类数的高斯混合分布模型参数估计问题，常见的做法是通过AIC(Akaike information criterion)和BIC(Bayesian Information Criterion)准则判断最佳的模型选择。AIC 是衡量统计模型拟合优良程度的一种标准，由赤池弘次创立发展，在这里用EAIC表示，定义为

式中：χ为模型个数；L为似然函数，该准则可以寻找最好地解释数据但包含最小自由参数的模型。

一般在选择高斯混合分布的最佳聚类数目时，选择AIC指标最小的模型对应的类数K*。在确定最优混合高斯分布的类数K*后，即可根据车头时距与饱和流率关系计算混合饱和流率。

数据经过混合分布估计参数后，对每个数据进行判别，当模型认为其符合第k类分布的概率最大时，该数据便被归为第k类，混合饱和流率S′为

式中：为属于第k类的车头时距数据数；u′k为该类分布的均值。

假设真实情况下，符合某固定前后车型的车头时距Ni,j的车头时距数据有ni,j个，均值为μi,j。则在此混合比例下，真实的混合饱和流率S为

S′和S的差值即为高斯混合模型的估计混合饱和流率的误差。

2.2 模型的求解

对于混合分布中含有的多个参数πk,μk,σk，直接应用极大似然估计方法计算，复杂程度高，不易求解，故使用EM(Expectation Maximization)算法进行估计。EM 方法简化了极大似然估计的计算，最大的优点是简单和稳定[11]。

引入一个K维的二值型变量z=[]z1,…,zk，表示样本由哪个分模型产生，zk∈{0,1} 且，即有且只有一个取值为1，其余为0。对样本集{x1,…,xΩ}，zk=1 表示该样本x由分模型k抽样得到，Ω代表样本数量。第n个样本xn对应的隐变量zn=[zn1,…,znK],n=1,…,N，取初始值开始迭代，EM算法步骤如下。

Step 1 E步

式中：γ(znk)为当前模型参数下第n个观测数据来自第k个分模型的概率。

Step 2 M步

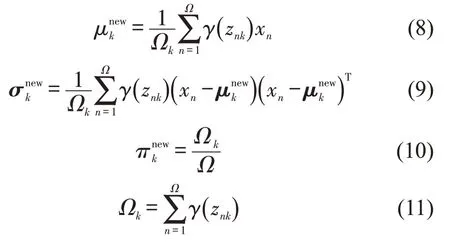
式中：μnkew,σnkew为新一轮迭代中第k个分模型的均值和方差；Ωk为被分配到第k个分模型的有效样本数。

Step 4 对不同K值的混合分布模型利用AIC指标进行评判，选取AIC指标最小的模型作为最佳模型。

3 实例分析

3.1 数据输入

选取杭州市环城西路-体育场路(环城西路96号)，丰潭路-萍水街(丰潭路566 号)，花蒋路-余杭塘路(余杭塘路)3 个交叉口某条车道作为应用案例，地理位置如图3所示。

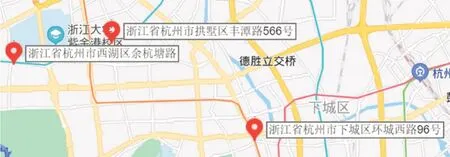
图3 数据采集点位地理位置Fig.3 Geographical location of intersections

采用摄像机人工拍摄2019年11月某工作日晚高峰时的过车视频，对视频进行逐帧分析对比，记录车辆车头通过停车线的时刻信息和车牌信息，时刻信息精确到0.02 s。计算同车道内连续2辆车通过时刻的时间差，得到车头时距。将所得混合车流的车头时距作为真实值，样本数为2293个，数据统计如表1所示。

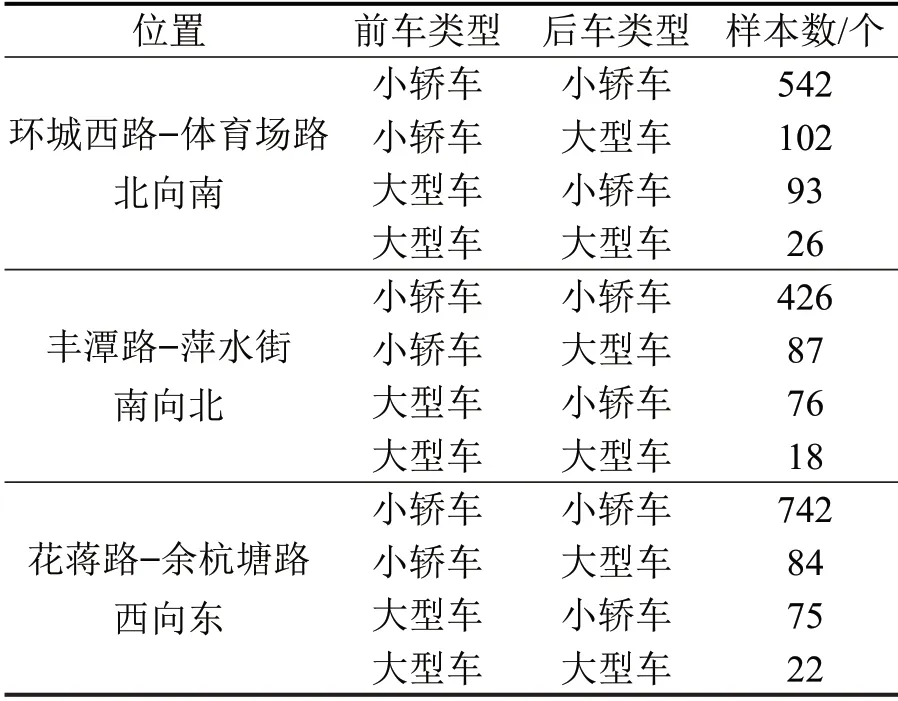
表1 车头时距统计表Table 1 Statistics of headway

考虑到自动车牌识别数据的时间戳精确到秒，采样时间的精度不够。为模拟ALPR数据，对采集的实测过车数据进行取整处理，分析自动车牌识别数据和真实数据由于数据采样带来的误差，如表2所示。

表2 模拟采样相对误差表Table 2 Relative error table of analog sampling

采样相对误差在1.6%～4.0%之间，数据误差在5%以内即可接受[10]，因此，自动车牌识别数据可以满足作为实际数据输入准确性的要求。

按照统计检验方法对获取的车头时距数据分别进行高斯混合分布和对数正态混合模型拟合，对车头时距数据分布在显著性水平0.05 下进行K-S检验，计算频率分布与理论分布两条累计分布曲线之间的最大垂直差D 值，D 值越小，说明越符合分布假设，结果如表3所示，3个测试路口的饱和车头时距数据均通过高斯混合分布检验，相比对数正态混合分布取得更小的D值。

表3 车头时距分布K-S检验显著性水平Table 3 Significance level of K-S test for headway distribution

3.2 模型求解

运用AIC判断高斯混合模型的高斯分布个数，AIC 指标值最小的K值个数就是最佳个数，例如，环城西路-体育场路模型的AIC分析，如图4所示，随着K值增大，AIC值先减小后增大，在K=2处取得最小值，其他两个交叉口得到相同结果。

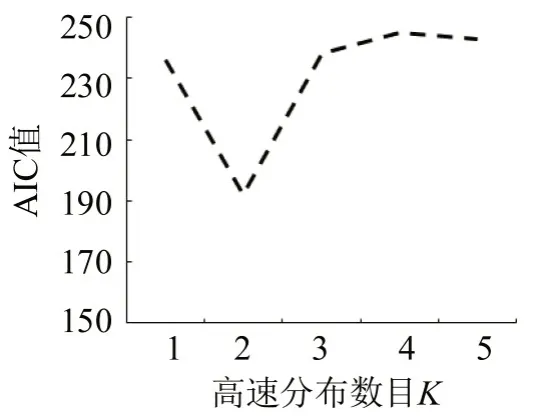
图4 环城西路-体育场路高斯混合分布个数与AIC关系Fig.4 AIC analysis chart of Huancheng West Road Stadium Road

根据数据分布特点，模型将其分为纯小型车组成的车头时距和混入大车的车头时距两种分布，3 个交叉口分别得到的高斯混合分布参数如表4所示，数据分布直方图和高斯模型拟合结果如图5所示。

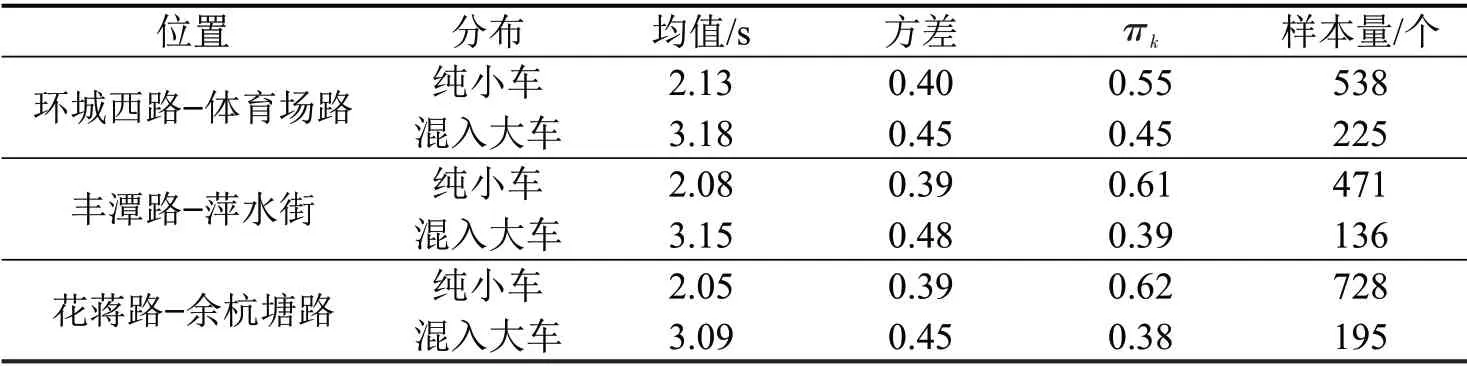
表4 高斯混合分布参数表Table 4 Parameters of gaussian mixture distribution

图5 数据分布和高斯模型拟合结果Fig.5 Data distribution and Gaussian mixture model fitting results

根据拟合结果，由式(5)和式(6)分别计算HCM实测法和本文模型拟合的混合饱和流率，以HCM法为标准，计算相对误差如表5所示。

表5 HCM法和模型拟合的混合饱和流率对比Table 5 Comparison of HCM method and model fitted mixed saturation flow rates

通常做法是使用HCM手册换算为标准小型车饱和流率用于配时，这一做法默认了调查数据与当下交通组成一致。表5表明两者计算结果非常接近，可以认为该方法的效果接近HCM法。但HCM法在目前技术手段下，只能通过人工调查数据计算，而本方法可以在检测器上自动采集数据计算，故本方法实际应用意义在于能在未知车型和交通组成条件下，合理地估计当前交通状态，能够自动化部署在检测器上，取代人工调查。

利用本案例数据，按城市道路工程设计规范[12]推荐的车辆折减系数，将数据换算成标准车流饱和流率，将模型拟合的纯小车车头时距分布换算成标准车流饱和流率，计算结果如表6所示。模型拟合结果接近于结合了大量工程实际的规范换算，说明本方法结果上接近工程实践。

表6 按规范和高斯混合模型计算所得标准车饱和流率Table 6 Saturated flow rate of standard cars calculated by Code and Gaussian mixture model method

为探讨模型在不同流量条件下的适用情况，以15 min为一个时间段，分别选取晚高峰的4个时间段，计算不同高峰时间段本文方法所得的混合饱和流率，如表7所示。极差系数在10%以内，说明本文方法具有一定的鲁棒性。

表7 不同高峰时间段混合模型计算所得混合饱和流率Table 7 Saturation flow rate of standard vehicle calculated by hybrid model at different peak periods

4 结论

本文提出基于自动车牌识别数据的混合交通饱和流率的实时估计方法，该方法能够自动部署，实时采集数据计算，案例计算结果与真实值相差在5%以内，效果接近于经典的HCM 法，准确性和可靠性高；同时，不同时间段内极差系数结果表明方法具有良好的鲁棒性，能取代人工调查，为未来交通信号控制系统的研究提供基础。