基于复杂网络的城市交通拥塞因子风险传播机理及其应用研究

胡立伟，范仔健，张苏航，郭治，殷秀芬

(昆明理工大学，交通工程学院，昆明650500)

0 引言

随着人民生活水平的不断提高，城市机动车保有量快速增长，交通拥塞逐渐成为影响城市交通系统正常运行、居民出行效率及居民生活质量的主要因素，科学治理刻不容缓。国内外学者对于交通拥塞影响因子分析开展了很多研究：Bian[1]等利用在线地图数据，建立多元线性回归模型来识别影响拥塞率的主要因素；许彬[2]通过构建基于分辨矩阵的属性约简算法模型并结合实测数据，提取出导致拥堵的关键因素。随着复杂网络理论的发展，众多领域也开展了相关应用。花玲玲[3]等利用复杂网络理论对铁路事故致因因素进行分析，研究表明，复杂网络用于因子分析的可行性和适用性。在交通领域复杂网络理论也取得了诸多成果：Wu[4]等利用复杂网络的SIR 模型描述道路交通拥塞的传播；Zhang[5]等基于复杂网络理论，分析交通网络复杂性的表征参数并建立拥塞疏散路径选择模型；雷凯[6]等将复杂网络传播动力学理论引入多式联运网络风险传播问题，进一步揭示了风险传播的复杂内在规律；Solé-Ribalta A.[7]等基于复杂网络中出现的临界现象，通过识别出城市道路网络中的拥塞热力点(重要节点)，分析拥塞热力点的传播作用和扩散范围。

综上，现有交通拥塞因子的研究集中于先分析关键因素，再制定相应的管控策略，没有考虑交通拥塞因子的风险传播特性以及因子之间的网络连接特性。而通过分析交通拥塞或交通风险在复杂网络上的传播，拥塞的疏散机理等研究成果可知，利用复杂网络理论研究城市交通拥塞因子风险传播机理是可行的。基于此，本文构建城市路网交通拥塞因子风险复杂网络模型，通过分析网络中不同重要度节点对风险传播的影响程度，同时引入目标免疫对传统的SIR 模型进行改进来分析风险网络的传播阈值和风险传播的变化特点，探索风险网络传播的控制策略和方法。在现实路网中，交通管控模型筛选出的核心节点，可有效降低风险的传播强度和传播速率，并为高效疏导和缓解交通拥塞提供理论支撑和参考。

1 交通拥塞因子风险网络构建

1.1 数据来源

以昆明市部分路网为试验对象，利用网络数据爬虫，标定昆明市主城区早(8:00-9:00)、晚(17:30-18:30)高峰时段6个月内的主要城市路网交通拥塞点，并对拥塞点进行实地调查以及查看拥塞点处的城市公交等监测平台记录，获取早、晚高峰城市实时流量、信号配时、道路状况等数据。深入分析诱发城市路网交通拥塞的风险因素，进而将风险因素分为驾驶人因素(D)、道路因素(R)和环境因素(E，包括自然环境和交通运行环境)3类。3类风险因素构成交通拥塞风险因素集为

鉴于城市道路网络交通拥塞因子风险分析的复杂性，因子选取时并不是越多越好，关键考虑因子在风险传播过程中所起的作用以及与昆明市实际拥塞状况的相关性。本着系统完整、科学合理、层次分明的原则，采用定性定量分析，结合昆明市拥堵区实地调查、车辆监测平台数据、文献萃取[1,2,8]和Delphi 法，选取城市交通拥塞因子共36 个，如表1所示。

表1 交通拥塞影响因子Table 1 Impact factors of traffic congestion

1.2 因子相关性分析

根据复杂网络理论，将诱发城市道路网络交通拥塞因子视为独立的节点，通过计算Pearson 相关系数分析影响因子间的相关性，确定节点间的边。将计算结果方差显著性水平0.05 且正相关性的因子两两相连，本文规定因子间不相关定义为0，因子间相关定义为1，从而构建0-1 邻接矩阵。在实际计算过程中，由于Pearson 相关系数不能区分因子间是何种相关关系，故本文基于Pearson 相关系数构建的复杂网络为无向网络。根据0-1 邻接矩阵，运用Gephi0.9.2 软件绘制无向相关影响因子复杂网络如图1所示。

图1 依据节点度渲染的Pearson相关系数网络Fig.1 Pearson correlation coefficient network rendered according to node degree

1.3 节点重要度k

使用Gephi0.9.2 软件对无向复杂网络中节点的度值、平均度、网络直径、图密度、平均路径长度、平均聚类系数、中介中心度和特征向量中心度等指标进行计算。得到部分复杂网络指标如表2所示。

表2 复杂网络指标计算值Table 2 Calculated values of complex network indicators

选取节点度值、中介中心度和特征向量中心度这3 个指标描述节点在网络中的重要程度k，且3 个指标均为效益型指标，值越大，对应节点的重要度越高。节点的度定义为与该节点连接的边数，连接边数越多，度越大，该节点就越重要；中介中心度是指网络中通过某节点最短路径的数量与全部最短路径数量的比值；特征向量中心度的取值受相邻节点影响，即连接的节点越重要，该节点也就越重要。

假设复杂网络有个n节点，每个节点用m个指标来描述。集合X表示复杂网络节点集，X={X1,X2,X3,…,Xn} ；Yij表示第i个节点的第j个指标，i=1,2,3,…,n,j=1,2,3,…,m。则复杂网络的节点指标矩阵为

上市公司对环境会计信息的披露情况，结果发现，在项目的年度报告中，披露环保投资率最高，达到 46.2%，其次是污染防治办法，环境税，环境风险，环境保护排污费和借款等，分别为28.4%，22.7%，18.7%和 10.4%，另外，各行业的环境会计信息均有不同，采掘业高达 100%，而纺织业、服装、皮毛业则只有11.1%，可以看出，披露的主体是在一些制造业等重污染行业，而且披露的信息主要是负担的环境成本，环境收益信息和未来的潜在风险信息披露较少，但已经披露的这些成本信息比较分散和随意，缺乏统一的标准，也没有设置专门的会计科目，缺乏专门的计量方法，难以形成货币性信息。

节点各指标的取值量纲不同，为方便计算，将W矩阵进行归一化处理，即

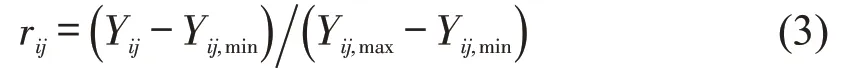
式中：Yij,min=min{Yij|i=1,2,3,…,n} ，Yij,max=max{Yij|i=1,2,3,…,n} 。归一化矩阵可记为R=(rij)n×m。

一般采用一致性经验法为节点的各个指标赋予权重，无经验可依时，多采用平均法加权规范化矩阵。

最后，利用理想方案对交通拥塞因子复杂网络中每个节点的重要度ki进行评估，ki值越大，则表示该节点在复杂网络中的重要度越大，计算公式为

图2 复杂网络节点重要度综合分析Fig.2 Comprehensive analysis of importance of complex network nodes

相关研究表明，当一个评价指标满足正态分布时，则表明该指标的第50、第85分位值可成为划分指标重要度的阈值。本文借鉴此方法，利用SPSS软件对36 个网络节点重要度进行正态分布检验，计算结果显示，节点重要度满足正态检验(显著性0.083＞0.05)。据此，利用节点重要度指标第50和第85 分位值将网络节点划分为3 类，第1 类是对网络影响最大的核心节点E，第2 类是对网络影响一般的普通节点F，第3 类是对网络影响最小的边缘节点G。

2 交通拥塞因子风险传播模型研究

风险在交通拥塞因子风险网络中的扩散是以点-线-面的形式传播的，且对关键节点的影响较大，这一过程就类似于传染病在复杂网络中的蔓延。基于此，结合风险传播理论，本文认为将交通拥塞因子风险在网络中传播模拟为传染病的传播过程是可行的。将交通拥塞因子风险传播过程中运行状态的数学描述简化为对风险因子感染比例的研究，对模型进行抽象化和改良。当某些因子被判断为核心影响节点时，通过相应的风险防范手段和响应措施对其加强，据此在模型构建过程中引入节点重要度k和目标免疫率ρk的概念。

2.1 加入k 和ρk 的SIR模型构建

(2)β为拥塞风险传染概率，λ为拥塞风险消散概率，两者与交通控制与管理、交通事件、交通流离散等多种影响因素有关，的大小表示交通拥塞因子风险传播集聚和消散的速度。相较于普通SIR 模型，在交通拥塞因子风险网络中，各相邻节点间的风险状态相互影响，且不同节点具有不同影响力，它们的传染率和恢复率也不同。影响力越大的节点其传染率就越大，恢复率则越小。定义3类节 点的传染率分别为βE、βF、βG，且满足1＞βE≥βF≥βG＞0；恢复率分别为λE、λF、λG，且满足0＜λE≤λF≤λG＜1。模型结构如图3所示。

(3)目标免疫是一种较为有效的免疫策略，针对复杂网络中节点重要度k大于85 分位且被定义为核心节点的网络节点进行免疫，在网络中表现为该类节点的边被移除，进而风险传播的可能途径大大减少。基于此，定义目标免疫概率ρk为

式中：ε为免疫的临界值，当重要度k≥ε时进行免疫。

根据以上分析，构建交通拥塞因子风险传播模型为

式中：SE(t)、SF(t)、SG(t)分别为S(t)中E、F、G 节点的比例；IE(t)、IF(t)、IG(t)分别为I(t)中E、F、G节点的比例。S(t)、I(t)、R(t)三者的数量关系为

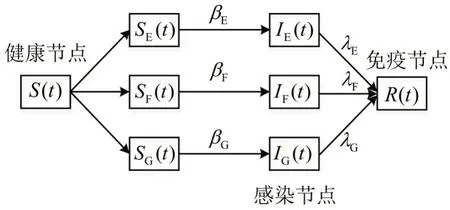
图3 交通拥塞因子风险传播模型结构示意Fig.3 Structure of risk propagation model of traffic congestion factors

2.2 模型求解

参考文献[9]中的阈值理论，在模型求解过程中，不考虑节点免疫的影响，取目标免疫概率ρk=0。将交通拥塞因子中已经被感染的比例I()t的最终表达式化解为

式中：σ为风险相对移除率，σ=，其中，NE、NF、NG为3 种节点在所有节点中所占比例。

2.3 传播阈值分析

为更直观地描述S(t)-I(t)平面上相轨线的变化规律及交通拥塞因子风险在网络上的传播阀值，由式(8)可得相平面轨线方程为

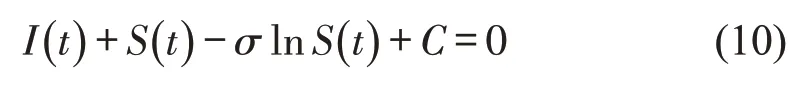
式中：C=I(0)+S(0)-σlnS(0)，进一步写成相平面上解曲线族为

由图4可知：随着相对移除率δ的改变，曲线出现的峰值时间节点也不同；令初始时刻t=0，则初始时刻网络中健康节点和感染节点的初始比例表示为(S(0),I(0))；随着时间t的增加，(S(t),I(t))沿轨迹线自右向左移动。当初始值(S(0),I(0))落在S(t)=σ右边时，I(t)会逐渐增大，拥塞因子风险加大，且当相应的网络中健康节点比例S(t)减小至S(t)=σ时，网络中的感染节点比例I(t)会达到最大值，而后随着S(t)的不断减小，I(t)又会逐渐降低；当初始值(S(0),I(0))落在S(t)=σ左边时，I(t)会逐渐减小直至为0，即城市道路网络交通拥塞因子风险减小并消失。因此，初始时刻网络中健康节点比例及各类节点的恢复率和传染率是影响交通拥塞因子风险传播的主要因素，这与早晚高峰时期交通拥塞因子风险的传播规律是一致的。根据上述可知，相对移除率是交通拥塞因子风险在复杂网络传播过程中的一个阈值。

图4 相轨线分析Fig.4 Phase trajectory analysis

3 模型应用分析

3.1 复杂网络核心节点控制

依据前文得出的节点重要度k进行排序，选取6 个重要的且可进行人为干预的节点作为控制节点，具体如表3所示。

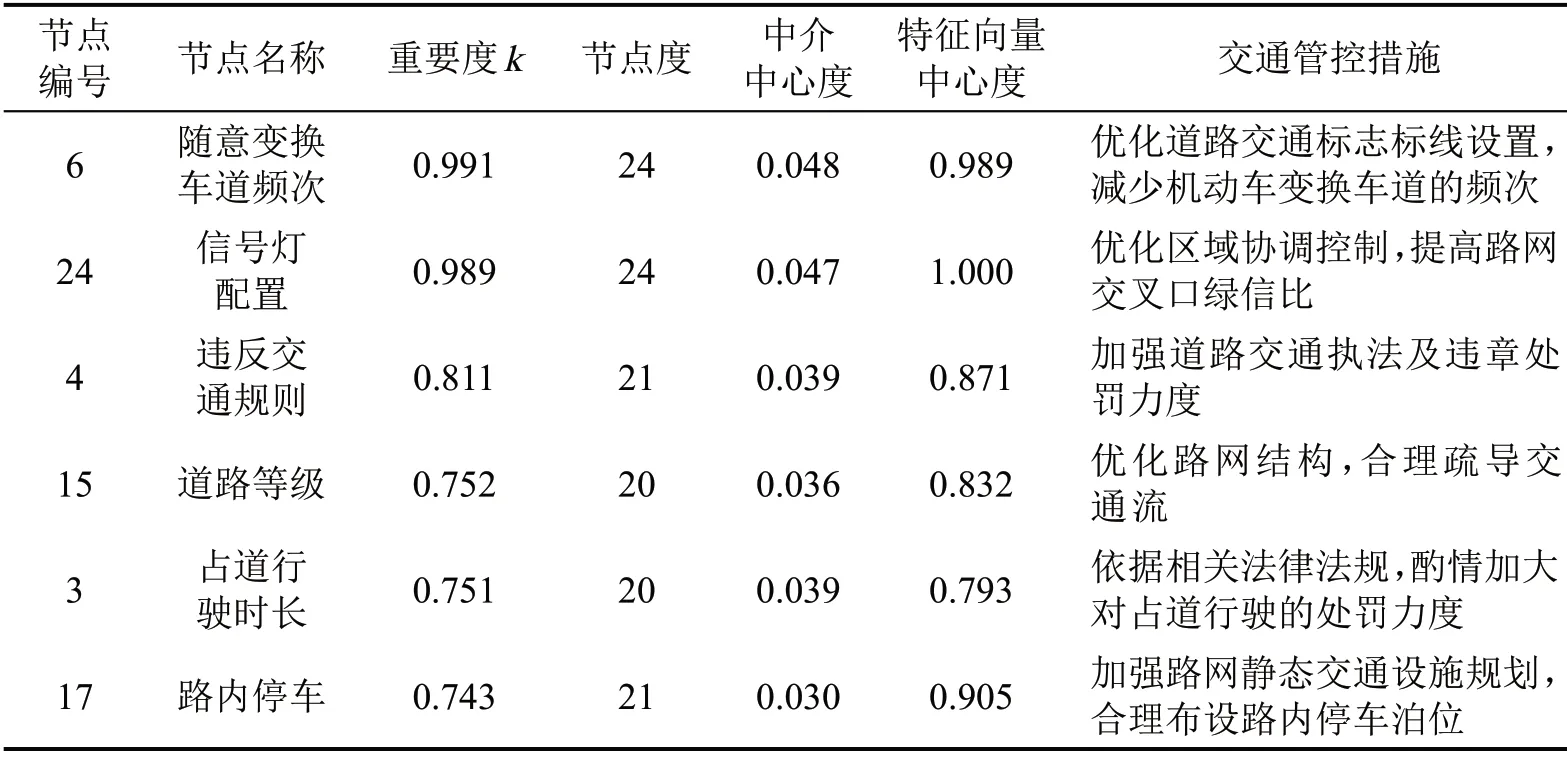
表3 复杂网络控制节点明细表Table 3 Detailed list of complex network control nodes

3.2 加入可控核心节点和目标免疫的网络传播过程分析

控制复杂网络中其他传播条件不变，根据网络地图历史数据标定感染概率βE=0.95、βF=0.60、βG=0.45，消散概率λE=0.10、λF=0.28、λG=0.50 ，初始感染节点选取1 号驾驶疲劳程度和16 号道路限速。基于筛选出的可控核心节点进行免疫，从重要度最大的6 号节点开始，按照重要度排序依次增加一个节点，直到6个核心节点全部免疫。分别取目标免疫率ρk等于0.000，0.028，0.056和0.112 进行传播分析，结果如图5所示。图5中单位时间t表示各节点从风险产生、发现、反应、判断，进而免疫控制的时间，现实中依据道路中普遍的红绿灯信号周期进行测算，单位时间t约为4 min。

依据图5分析可知，加入可控核心节点和目标免疫后，与没有核心节点免疫控制相比较，当ρ=0.028 时，感染节点峰值比例降低5.40%，感染高峰时间节点延后0.39t；当ρ=0.056 时，感染节点峰值比例降低11.42%，感染高峰时间节点延后0.79t；当ρ=0.112 时，感染节点峰值比例降低21.22%，感染高峰时间节点延后1.18t，免疫率ρ的取值基本与感染节点峰值比例值成反比。且ρ取0.028，0.056，0.112 时，相较于不加免疫控制，健康节点到达平衡状态的速率较慢，恢复节点到达平衡状态的速率较快。图5中数据表明，通过对网络中核心节点筛选并加以直接免疫控制，交通拥塞因子风险的程度得以降低，而风险的恢复速度有较为明显的提升。

图5 SIR复杂网络传播图Fig.5 SIR complex network propagation diagram

4 结论

(1)验证了复杂网络理论在城市交通拥塞因子风险传播领域的可行性和适用性。在现实中，通过管控交通拥塞核心影响因子来缓解路网拥塞程度，为实际的城市交通管理提供一定参考。

(2)依据网络节点的度值、中介中心度和特征向量中心度的综合分析，得出网络节点重要度k的概念，同时，本文构建的基于复杂网络的交通拥塞因子风险传播SIR 模型可对风险传播的动力学过程进行较好的仿真模拟。

(3)对核心节点进行直接免疫控制，免疫概率ρ分别取0.028，0.056，0.112 后计算分析可知，免疫概率ρ取值基本与感染节点峰值比例值成反比。加入核心节点免疫控制后，交通拥塞因子风险的传播规模和传播速率得到较好地控制。