高速公路收费广场车道合理化配置研究

钱超，李思言，王彦锋

(1.长安大学，电子与控制工程学院，西安710064；2.深圳高速公路股份有限公司，广东深圳518026)

0 引言

收费广场是高速公路瓶颈路段，高峰及特殊时段(节假日、交通事故、恶劣天气等)极易形成大面积拥堵，严重影响高速公路路网通行效率。特别是省界收费站由收费造成的长时间拥堵，社会意见尤为强烈。鉴于此，国家提出取消高速公路省界收费站，建立全国高速公路“一张网”运营体系，实现车辆快捷收费，从根本上解决收费站拥堵问题。2020年初，29 个联网省份共计487 个省界收费站撤销，高速公路实现全国联网收费。随着取消省界收费站工作的推进，ETC 用户数和使用率也在同步增长。截至2020年5月，全国高速公路ETC车辆占比达64.09%，同比增长21.89%，但仍距预期的90%使用率有一定差距。ETC 系统的便利性和快捷性促进其加快普及，但“一刀切”式的车道改造(仅保留最右侧一条ETC/MTC 混合车道)与低于预期的ETC使用率也造成部分匝道收费站出现拥堵问题，如2020年5月全国日均仍有434个收费站出现500 m以上的拥堵缓行。因此，需结合实际交通量、交通组成及不同收费方式比例，科学确定收费广场ETC车道和混合车道配置方案，从而达到保障车辆便捷高效通行、提高收费广场通行效率的目标。

为缓解收费站拥堵、提升收费广场通行效率，国内外相关学者在收费站通行能力计算方法[1-2]、不同收费亭布局下的收费广场通行能力[3]等方面开展了大量研究，提出了收费广场拥堵消散控制策略[4]；通过建设、运营成本计算，提出成本最低时的车道配置方案[5-7]。此外，鉴于收费车道数量对服务水平的影响[8]，通过不同车道布设方案下的服务水平对比评价，提出了最优车道配置方案[9-10]。综上所述，国内外学者从多角度探索了收费广场通行能力及单一类型车道配置方案，但针对不同ETC使用率条件下多种类型收费车道综合配置研究仍较匮乏。

鉴于此，本文开展收费广场车道合理化配置实证研究，结合平、高峰时段交通量，对比分析不同ETC使用率及车道配置方案下收费广场通行效率，探索收费广场常态化交通拥堵解决方案。

1 交通行为模型与通行效率指标

1.1 交通行为模型

收费广场交通流具有间断和随机的特性。车辆减速进入广场后，驾驶员综合车道排队及收费方式进行车道选择，换道至目标车道后跟随前车排队缴费，具体过程如图1所示。

(1)跟驰模型

基于生理-心理模型，Wiedemann 通过行为阈值划分跟驰状态，建立起Wiedemann74 模型和Wiedemann99 模型[11]。因收费广场车辆密度大，车辆行驶缓慢，行驶情况复杂多变，宜采用Wiedemann74模型，车辆跟驰前、后车最小间距d为

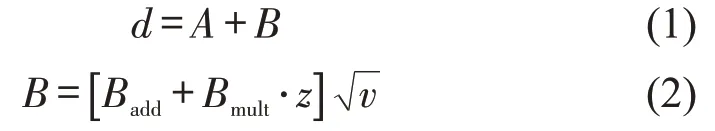
式中：A为平均停车间距(m)；B为最小期望跟驰距离(m)；Badd为安全距离附加部分；Bmult为安全距离倍数部分；z为随机因子[0,1]，服从均值为0.5，标准差为0.15的正态分布；v为车速(m·s-1)。

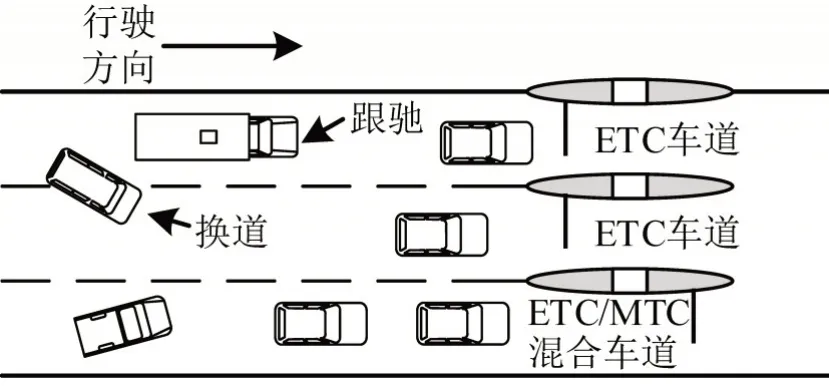
图1 收费广场交通行为Fig.1 Traffic behavior in toll plaza

(2)换道模型

目标车s 若通过换道进入前车l 与后车f 之间的目标车道，需同时满足换道后目标车s′与前车l′间隙gl、后车f′间隙gf均不小于给定的最小可插车间隙，则目标车s 可并入目标车道。图2为车辆换道模型的时间-位移图。

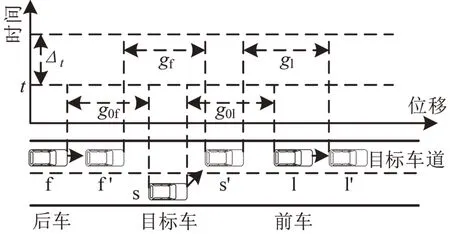
图2 车辆换道时间-位移Fig.2 Lane-changing time-displacement

换道时间Δt内，上述3车行驶速度分别为vs、vf、vl，则换道结束时车辆间距为

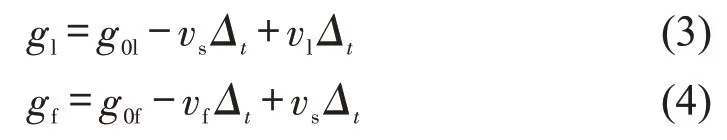
式中：g0l为换道前目标车与后车间距(m)；g0f为换道前目标车与前车间距(m)。

若目标车在换道过程中以加速度as减速(或加速)，且后车主动以加速度af减速，则此时的车辆间距为

为保证车辆s和车辆f、l不发生碰撞，在最小安全距离满约束条件下，才可实施换道行为[12]，约束条件为

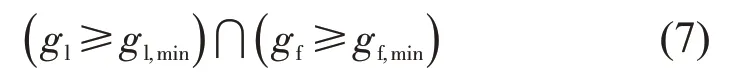
式中：gl,min为目标车与后车最小间距(m)；gf,min为目标车与前车最小间距(m)。

1.2 通行效率评价指标

选取收费广场断面交通量、单车平均延误作为通行效率评价指标。

(1)交通量

收费广场断面交通量q是指单位时间内通过收费广场某一断面的车辆数，计算方法为

式中：N为观测时间内通过收费广场断面的车辆数；T为观测时间。

(2)平均延误

平均延误表示单位时间内通过收费广场车辆延误时间的平均值，其计算过程如下。

①车辆进入收费广场的减速时间t1为

②车辆在收费广场的平均逗留时间W为

③车辆驶离收费广场的加速时间t2为

④平均车辆延误D为

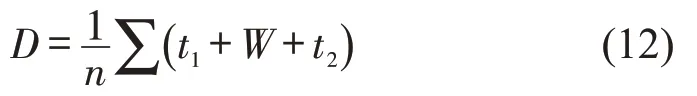
式中：v1为进入收费车道时的速度(m·s-1)；v′为车辆驶入收费区域时的速度(m·s-1)；v″为车辆驶出收费区域时的速度(m·s-1)；a1为车辆减速驶入收费区域的减速度(m·s-2)；a2为车辆加速驶离收费区域的加速度(m·s-2)；Wq为平均排队时间(s)；E[]S为服务时间期望值(s)；D为平均车辆延误(s·veh-1)；n为单位时间通过的车辆数。

2 收费广场建模

以深圳机荷高速公路福民收费站(出口方向)为研究对象，采用Vissim 8.0 建立包含匝道和收费广场的仿真模型。

2.1 路网模型

机荷高速主线东、西双向车辆经匝道1 和2 驶入福民收费站，缴费后通过匝道3 和4 进入城市路网，如图3所示，4条匝道基础参数如表1所示。

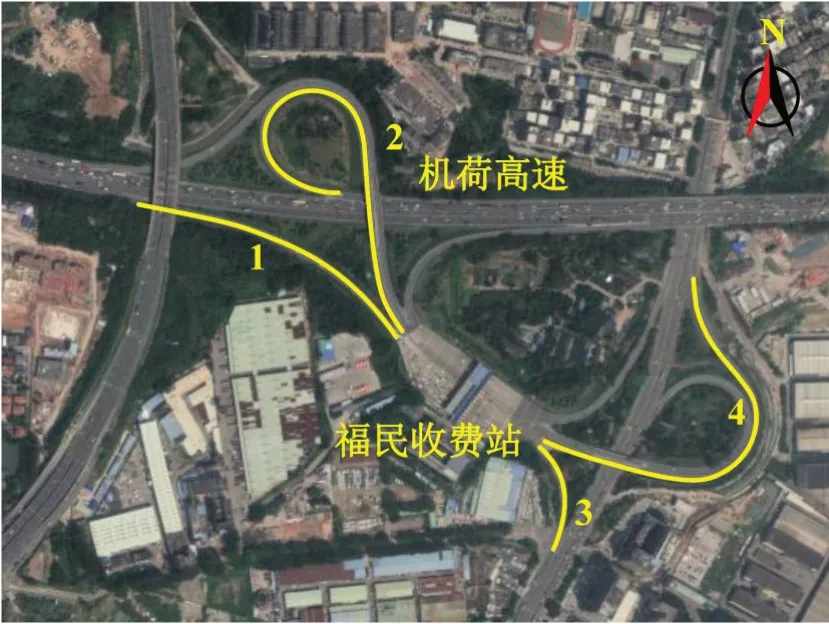
图3 福民收费站匝道布局(出口方向)Fig.3 Ramp layout of Fumin toll station(exit direction)

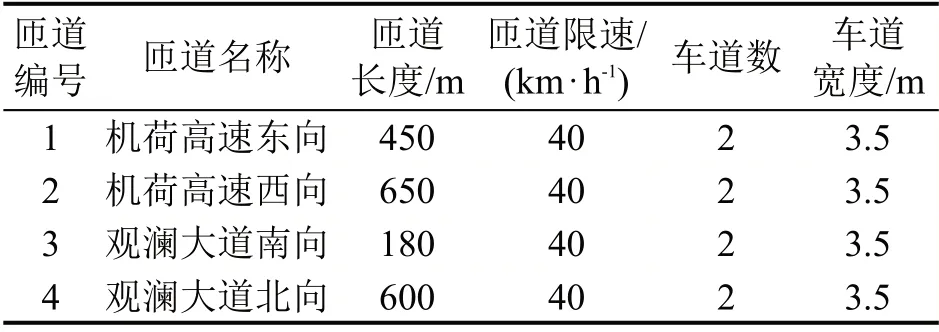
表1 匝道基础参数Table 1 Basic parameters of ramps

目前，福民收费站出口方向共有9 条车道，其中，ETC 车道4 条(编号为51、52、54 和55)，ETC/MTC 混合车道3 条(编号为57、58 和59)，未改造的MTC 车道2 条(编号为53 和56)。除最外侧车道为超宽车道(4.5 m)，其余车道宽度均为3.2 m，具体布局如图4所示。

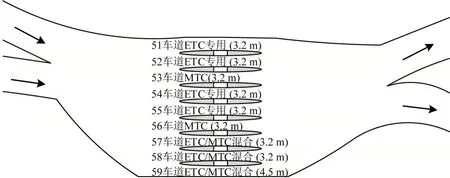
图4 福民收费广场出口车道布局Fig.4 Layout of Fumin toll plaza(exit lanes)

2.2 参数初始化

结合对微观交通仿真模型参数的标定，以及对跟驰、换道模型的参数分析，选取对收费广场交通运行影响较大的参数进行初始化，如表2所示。

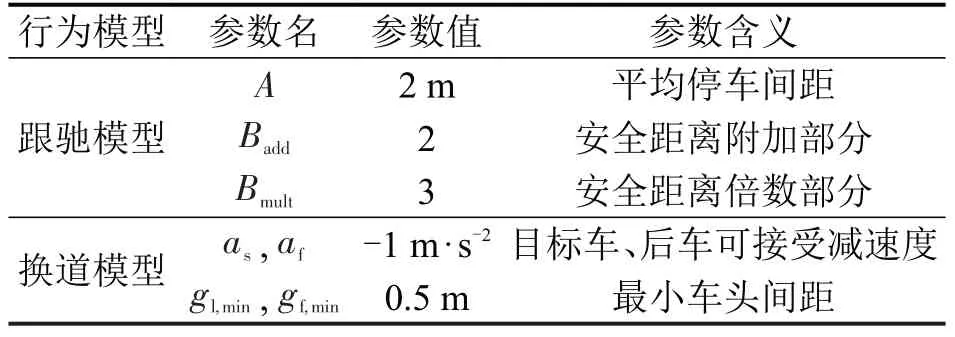
表2 车辆仿真参数Table 2 Vehicle simulation parameters

2.3 路网对象

(1)路径选择

在仿真模型中，合理的路径选择能够更准确地模拟车辆在收费广场的通行行为，故为不同类型车道分别设置允许通行的车辆类型，车辆根据预置的路径自主选择最优车道通行。

(2)服务时间与期望速度

由于车型及货车载重差异，各型车辆通行收费广场速度有别，同时缴费方式也对服务时间产生影响。为保证仿真结果的准确性，结合福民收费站监控视频分析，计算得到真实环境下收费广场分车型期望速度及MTC 方式平均服务时间，具体结果如表3所示。

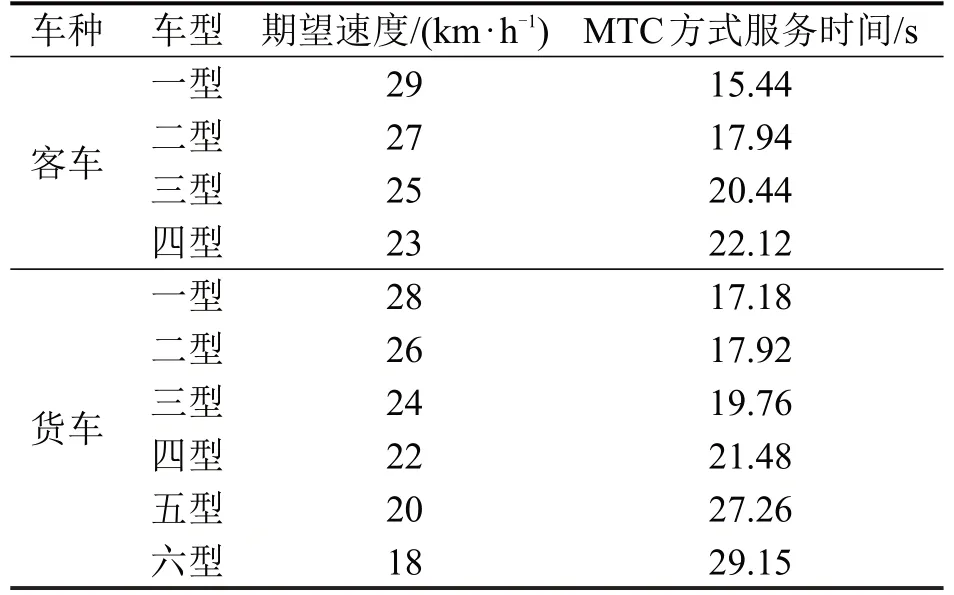
表3 分车型期望速度与MTC方式服务时间Table 3 Desired speed and MTC service time for different vehicle categories

3 实例分析

3.1 分车型交通量

应用福民收费站一周收费数据(2020/5/18-2020/5/24)，汇总统计得到不同支付方式下客、货车交通量时序图，如图5所示。

由图5可知，客、货车交通量均具有显著的日周期特征，平峰时段能反映收费广场常态运行状况，高峰时段对通行效率影响最大。选取平峰小时(2020/5/18, 11:00-12:00)和高峰小时(2020/5/18,18:00-19:00)开展仿真分析，以上时段分车型交通量及ETC使用率如表4所示。

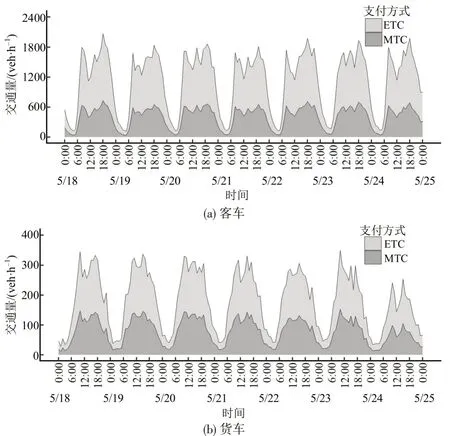
图5 交通量时序结果Fig.5 Sequential results of traffic volume

表4 平峰和高峰小时分车型交通量及ETC使用率Table 4 Traffic volume and ETC utilization rates for different vehicle categories during usual and rush hour

3.2 仿真及车道配置方案

福民收费站现状车道配置方案下的高峰时段车辆平均延误为60.23 s·veh-1，若将两条MTC车道改建为ETC/MTC 混合车道，即4 条ETC 车道、5 条ETC/MTC 混合车道，平均延误降为53.09 s·veh-1，减少11.85%，通行效率显著提升。因此，后续配置方案中均以混合车道取代MTC 车道，并以ETC 车道数为调优参数，根据通行效率评价指标确定不同ETC使用率下收费广场最优车道配置方案。

采用“ETC_Nlane_UETC”的方式命名仿真方案，其中，Nlane表示ETC专用车道数，UETC表示客/货车ETC使用率(%)。具体仿真方案设计如下。

(1)输入流量分别为平峰和高峰小时的交通量；

(2)UETC以10%为初始值，增长率为20%，最高为90%；

(3)Nlane以1 为初始值，依次增加，最多为8(保留至少1条ETC/MTC混合车道)。

综上，共计2×5×8=80组仿真方案，车道布设位置如表5所示。

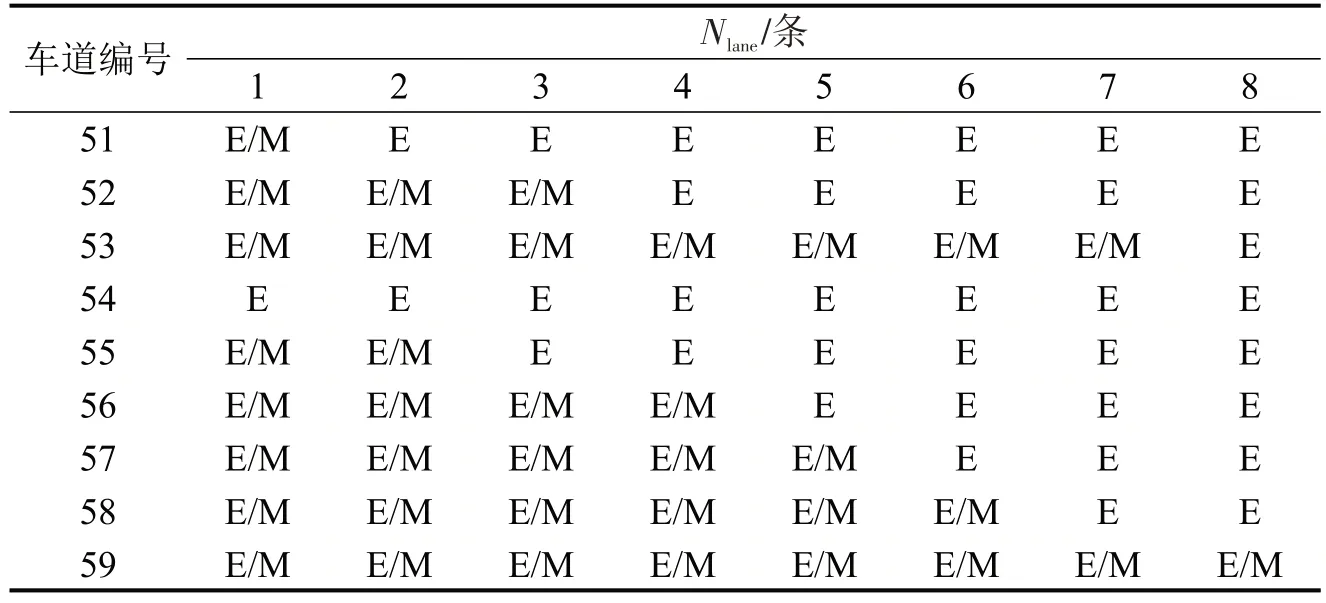
表5 ETC专用车道布设位置Table 5 Configuration of ETC lanes

3.3 仿真结果

(1)模型验证

收费广场交通运行微观仿真平台如图6所示。为检验仿真模型准确性，分别对平峰时段和高峰时段广场运行进行仿真分析，具体结果如表6所示。由表6可知，福民收费广场平峰时段和高峰时段交通量仿真结果与实际结果的平均绝对误差分别为3.46%和6.45%，表明车辆出行行为模型参数设置合理，仿真模型通过验证。

图6 收费广场仿真运行Fig.6 Operation simulation of toll plaza

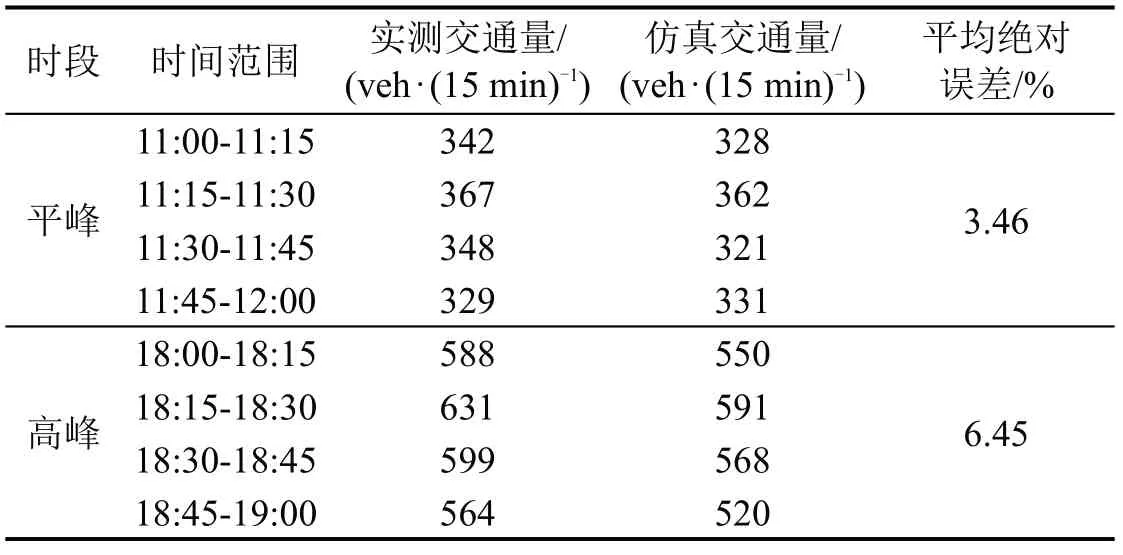
表6 仿真结果及误差Table 6 Simulation results and errors

(2)车道配置方案分析

平、高峰时段福民收费广场仿真结果分别如图7和图8所示，图7(a)、图8(a)中虚线分别表示平、高峰时段交通量。

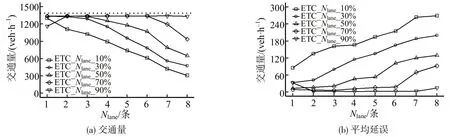
图7 平峰时段仿真结果Fig.7 Simulation results during usual hour

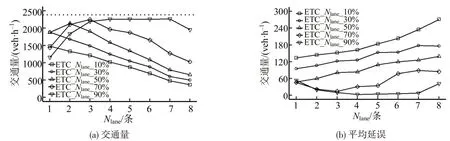
图8 高峰时段仿真结果Fig.8 Simulation results during rush hour

平峰时段：ETC使用率UETC≤50%时，广场通行效率随ETC 车道数Nlane增加而下降，平均延误较高，广场发生拥堵；UETC=70%时，通行效率随Nlane的增加先平稳上升后降低，车辆延误先随Nlane小幅度增加，后因过多的ETC 车道不能满足MTC 车辆的通行需求而迅速上升；UETC=90%时，通行效率随Nlane增加呈现平稳提升趋势，车辆延误最低，广场保持畅通状态。增设的ETC 车道可以提升广场通行效率，因MTC车辆数少，仅保留一条混合车道对通行效率影响较小。

高峰时段：UETC≤30%时，通行效率变化趋势与平峰UETC≤50%情况相同；UETC介于50%～70%时，通行效率随Nlane的增加先升后降，且车辆延误在UETC=70%时先下降后小幅度上升；UETC=90%时，Nlane≤3无法满足车辆快捷通行需求，此时最佳车道配置方案为4 条ETC 车道、5 条ETC/MTC 混合车道，单车平均延误仅为2.93 s·veh-1，较福民收费站目前的60.23 s·veh-1下降95%。仅保留1 条ETC/MTC混合车道的配置方案(即Nlane=8)下，单车平均延误为41.43 s·veh-1，可见此种方案并非最优，MTC车辆会影响广场整体通行效率。

4 结论

依托开发的福民收费广场交通运行微观仿真平台，对比分析了不同ETC使用率及车道配置下收费广场的通行效率，具体结论如下。

(1)仿真平台对平、高峰时段的仿真误差分别为3.46%和6.45%，表明车辆行为模型、期望速度、服务时间等仿真参数设置合理，为仿真研究顺利开展提供了基础平台。

(2)福民收费站目前ETC 总体使用率约为63.81%，高峰时段单车平均延误为60.23 s·veh-1。如将ETC使用率提升至90%，同时将现有2条MTC车道改建为ETC/MTC 混合车道，平均延误可降至2.93 s·veh-1，降幅达95%。

(3)收费广场需结合实际交通量、交通组成及ETC 使用率开展车道合理配置研究，未来应深挖ETC 市场潜能，进一步扩大使用率，提升收费广场通行效率。