带填充墙预制混凝土框架抗连续倒塌分析

张景博, 杨 健, 王斐亮

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

结构的连续倒塌是在结构正常使用的情况下，由于偶然荷载作用导致结构局部破坏，进一步导致建筑整体倒塌或者与初始破坏原因不成比例的局部坍塌.建筑的连续倒塌会造成巨大的财产损失甚至人员伤亡，需要引起重视.

失效柱的部位对于结构的连续倒塌有着重要的影响.于晓辉等[1]通过建立宏观模型，分析了在中柱失效时梁下的承载表现，结果发现在考虑悬链线机制时得到的荷载放大系数大于2.Dat等[2]分别对短边中柱和内柱进行移除，提出了一种混凝土柱抗连续倒塌的简化评估方法.Fu等[3]对带有复合地板的钢框架进行研究，移除角柱和内柱，并考虑了板的纵横比和边界条件等参数的影响.Wang等[4]考虑了钢筋与混凝土的变形协调，提出悬链线阶段的计算方法.

填充墙作为结构构件之一,其对框架的抗连续倒塌有一定影响.目前，填充墙的解析分析法主要为宏观分析模型，如等效压杆模型[5].高润东等[6]总结了国内外砌体填充墙等效压杆的简化计算方法，考虑填充墙开洞的情况，并在此基础上进行数值模拟研究.孙立建等[7]研究了外挂混凝土墙钢框架，考虑跨高比、轴压比、混凝土强度和填充墙厚度等参数的影响，并对等效压杆宽度公式进行了修正.在建筑的实际使用过程中，填充墙往往呈不对称分布，其对框架连续倒塌表现的影响与对称分布填充墙不同，且框架结构受力机制研究和计算方法尚不完善.《建筑结构抗倒塌设计规范》[8]中提出，在悬链线机制计算时可以取中柱位移为跨度的0.2倍，但是此建议值根据无填充墙PC框架提出，实际情况中填充墙可能会对结构的延性产生影响，并且PC框架结构的延性也可能发生变化，因此该建议值的适用性尚需验证.

本文提出基于等效压杆的填充墙框架计算模型，基于无填充墙预制混凝土(PC)框架试验和双填充墙PC框架试验建立有限元模型，验证参数的正确性.在此基础上，建立单填充墙有限元模型，并分别对无填充墙、双填充墙和单填充墙PC框架梁机制以及悬链线机制阶段的抗力建立解析公式.研究结果可以为文献[8]中关于PC框架结构的内容提供依据.

1 力学模型

1.1 填充墙简化模型

考虑填充墙对PC框架结构工作性能的影响，主要采用两类方法对填充墙进行处理：将填充墙简化为等效压杆的宏观模型法和将填充墙划分成大量单元的有限元法[5].宏观模型法通常只考虑填充墙受压，而不考虑其受拉的情况.因此，在涉及往复地震波的研究中，通常将填充墙简化为双对角的等效压杆以方便计算.对于单向位移加载的形式，只将填充墙延一条对角线简化.

在对单填充墙PC框架进行有限元分析时，填充墙不对称分布会导致中柱的平面内偏转，而无填充墙和双填充墙PC框架无此现象.因此，可以根据不同填充墙的受力特点可采取不同的简化方式.

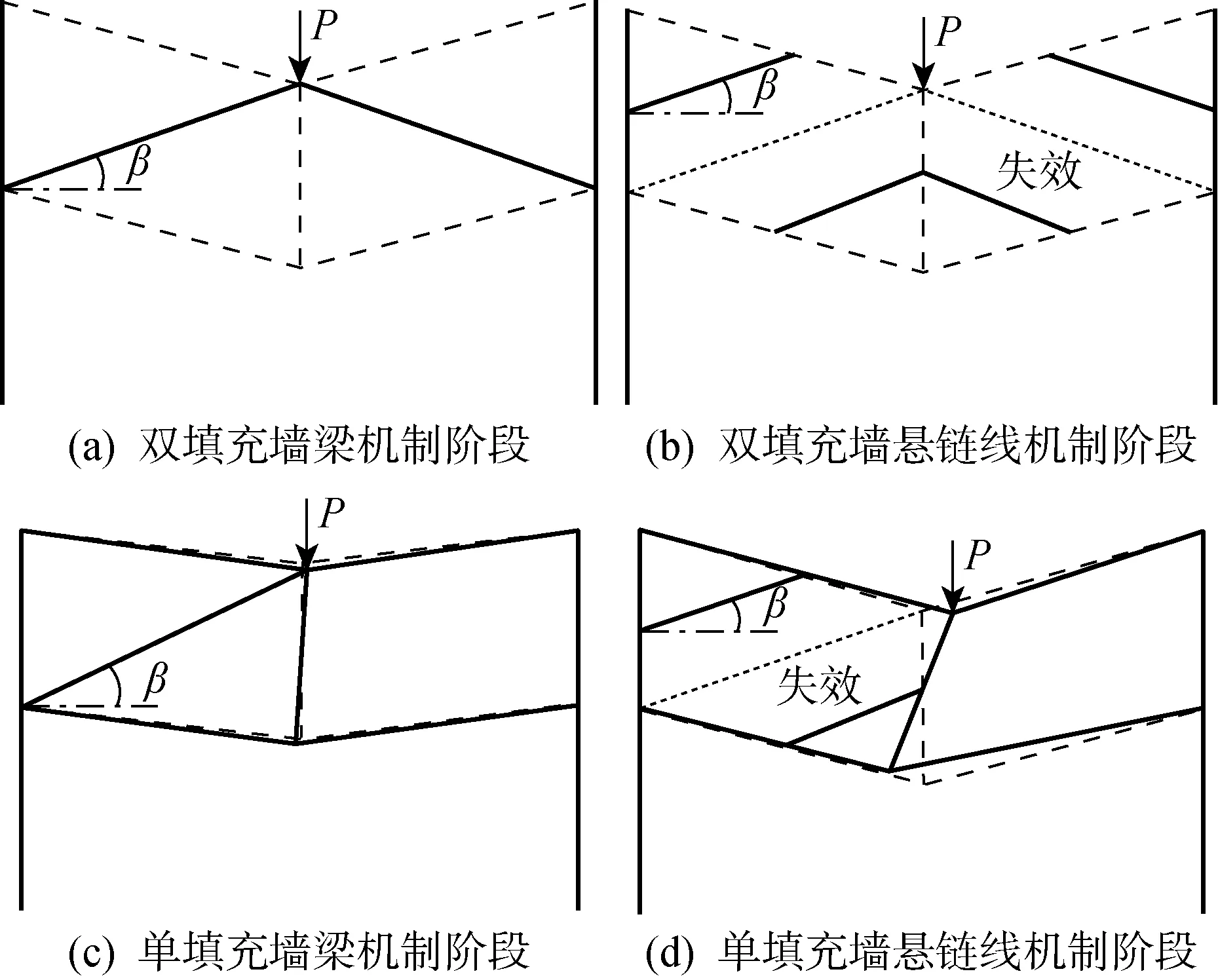
图1 填充墙等效压杆模型Fig.1 Equivalent strut models of infill wall

图1为填充墙等效压杆模型.由无填充墙和双填充墙PC框架的试验结果[9]可知，填充墙在梁机制阶段可以提供良好的协同抗力，因此在梁机制阶段采用如图1(a)所示的单压杆.其中，P为施加在中柱顶部的荷载，β为等效压杆与水平线之间的夹角，且

(1)

式中：Hinf为填充墙高度；Linf为填充墙长度；Δ为中柱位移.

在悬链线阶段，填充墙发生以对角压溃为主的破坏[9]，如图2所示.压溃后填充墙的承载能力明显下降，未经压溃的填充墙仍可以发挥一定的承载作用.因此在悬链线阶段，当单压杆失效时，填充墙受压区域向对角线两侧移动，未受压区域继续发挥作用.为方便计算，将三杆模型[10]进一步简化为如图1(b)所示的两根平行于原单压杆的从梁中部到柱中部的短压杆.

图2 填充墙破坏情况[9]Fig.2 Diagram of damaged infill wall[9]

对于填充墙不对称分布的情况，梁机制和悬链线机制阶段的计算分别采用如图1(c)和(d)所示的简图.根据有限元模拟结果，在该情况下，填充墙不对称分布导致中柱左右两侧的刚度不同，从而使得中柱发生偏转.由于受到填充墙的横向力，中柱顶部偏向无填充墙处，中柱底部则偏向有填充墙处.中柱的偏转角度较小，为简化计算，假设中柱围绕柱子中点旋转.在梁机制阶段，中柱顶部的偏移会对填充墙抗力的发挥产生影响，因此需要引入不对称系数以对填充墙的等效宽度进行折减.由于压杆取的端点分别是梁和柱的中点，所以β与填充墙对角平行，且偏转值相对于跨度较小，在计算时采用双填充墙中的方法.

压杆等效宽度的计算是将填充墙简化为压杆过程中的关键.考虑填充墙和周围框架的相对刚度，基于大量试验数据计算得到相对刚度参数[11-13]：

(2)

式中：Em为填充墙弹性模量；tinf为填充墙厚度；α为填充墙对角线夹角；Efc为填充墙周围框架构件的弹性模量；Icot为填充墙周边柱的截面惯性矩.在梁机制阶段，单杆主要由两边的柱子支撑，因此Icot取框架柱子的惯性矩；在悬链线阶段，两根等效压杆两端由梁和柱分别支撑，因此Icot取梁和柱惯性矩的平均值.

根据文献[14]进行等效宽度计算.在进行简化时，单填充墙只考虑一条对角线，因此基于面积相等原则[15]，利用下式[14]对等效宽度进行一半折减：

(3)

(4)

Em=900σinf

(5)

式中：a为等效压杆宽度；σinf为填充墙强度.

由填充墙提供的抗力为

Pinf=ηatinfσinfsinβ

(6)

式中：η为在梁机制阶段考虑不对称分布的填充墙等效压杆后的不对称系数，且

(7)

式中：Sbeam为梁截面面积；E1为梁截面材料的弹性模量.对于双填充墙和无填充墙框架，η恒为1.

填充墙与周围框架可以有不同的连接形式，以上简化方法适用于未与周围框架采用加强连接方式的墙体，例如仅施加简单防侧倾措施的填充墙和砌体填充墙.而采用了拉结措施的墙体由于受到可靠连接的作用，填充墙的受力状态可能发生改变.若填充墙更大程度地参与工作，则等效宽度会增大，同时可能导致另外一条对角线的角部受拉.

1.2 框架简化

由于中柱竖向位移相对较小，所以梁能够提供的竖向拉结抗力有限.假设荷载仅由支座处的弯矩提供，中柱节点仅对荷载分配产生影响，由于框架对称，所以不考虑中柱节点对荷载分配的影响.无填充墙框架在梁机制阶段框架受力如图3所示.其中，li(i=1,2)为框架跨度，Mpj(j=1,2,3,4)为边柱处塑性铰弯矩，Pc为无填充墙梁机制阶段峰值荷载，且

(8)

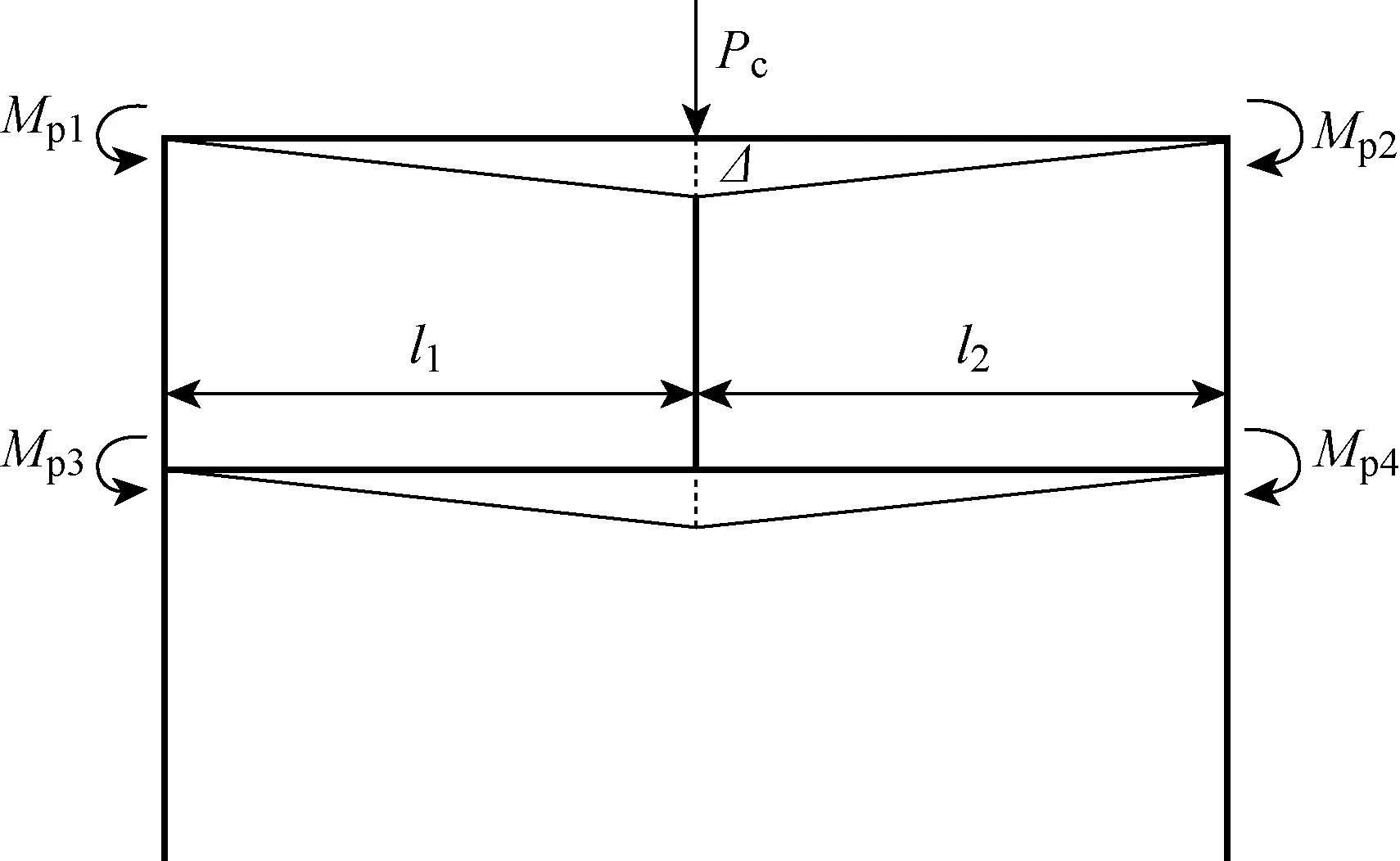
图3 梁机制阶段计算模型Fig.3 A beam mechanism calculation model

塑性铰弯矩为

Mp=α1fcξbh0b(h0-0.5ξbh0)+

(9)

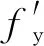
(10)

式中：β1为系数，当混凝土强度低于C50时，β1=0.8；fy为钢筋屈服强度设计值；Es为钢筋弹性模量；εcu为非对称受压时混凝土极限压应变.

当竖向位移达到一定程度时，结构由梁机制转变为悬链线机制.此时混凝土已被拉坏，不再参与工作，荷载主要由纵向通长钢筋承担.无填充墙框架悬链线阶段的结构受力如图4所示.其中，Pe为无填充墙悬链线阶段峰值荷载，FT为钢筋的极限拉力，Fj为梁内拉力，γj为拉力与水平线夹角，且

Pe=∑FTsinγj

(11)

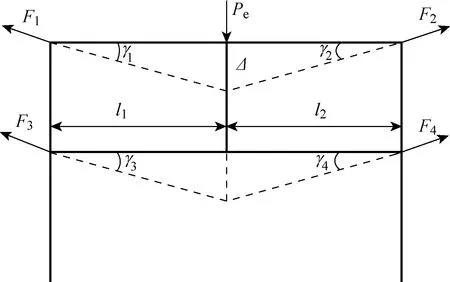
图4 悬链线机制阶段计算模型Fig.4 A catenary mechanism calculation model

(12)

式中：As为通长钢筋截面面积；fT为钢筋强度.

2 有限元验证

2.1 模型介绍

梁柱截面尺寸和配筋如表1所示.钢筋锚固深度为155 mm，其中梁内上翼缘为通长钢筋.填充墙厚度为100 mm，填充墙和梁柱采用C30混凝土材料.采用Abaqus软件建立有限元(FE)模型，实际结构经3∶1缩尺得到试验框架尺寸，如图5所示.

表1 梁柱构件参数Tab.1 Parameters of beam and column

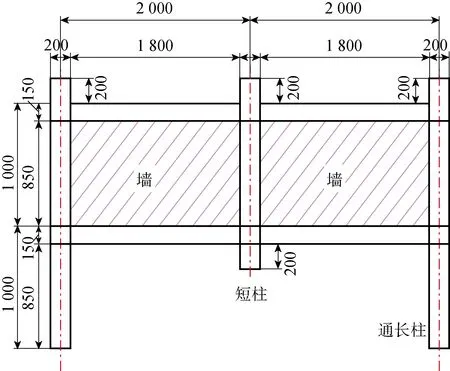
图5 对称墙框架示意图(mm)Fig.5 Diagram of frame filled with symmetric walls (mm)

模型中梁、柱填充墙均采用C3D8R实体单元，钢筋采用T3D2单元，钢筋和混凝土采用嵌入区域(embeded region)类约束.通过试验观察发现，预制梁构件和后浇带之间的界面无明显滑移，可视为完全黏接.填充墙与周边框架采用硬接触以确保两者之间不产生穿透，填充墙与周边框架的摩擦系数取0.1.在中柱与梁的接触面中，梁后浇带侧面与中柱侧边采用tie接触耦合，面与面之间可以传递拉力和压力且不会产生相对位移；在梁与边柱接触面中，梁的预制段侧面与边柱侧面也采用tie接触.边界条件如图6所示，分别将边柱节点外表面和相邻框架接触的部位以及边柱底面与参考点耦合，再对参考点施加边界条件.限制中柱参考点(RP-1)在x方向的位移，确保不发生偏心.框架的两个边柱底部和地面相连，因此限制参考点(RP-2,3)在x，y，z方向的位移.在实际情况中，子结构并非独立存在，而是与周边框架相连.此模型不考虑上部结构对下部框架抗力的贡献，仅将上部结构传递的荷载施加在参考点上.两侧框架的约束将会对框架结构的承载特性产生一定影响.为模拟周边框架对框架柱的约束，分别在边柱的中、上部参考点(RP-4～RP-7)施加约束，限制x和z方向的位移.预制段和中柱钢筋材料采用如图7所示的双折线模型.其中，σy为屈服应力，σu为极限应力，ε0为屈服应变.梁柱内拉结筋的弹性模量为206 GPa，泊松比为0.3.当钢筋的σy=430 MPa时，塑性应变为0；当σu=550 MPa时，塑性应变为0.1，箍筋的σy=300 MPa.混凝土材料的弹性模量为32.4 GPa，泊松比为0.2.定义混凝土损伤塑性参数[17]：膨胀角φ=30°，流动势偏移量ε′=0.1，双轴极限抗压强度与单轴受压极限强度之比fb0/fc0=1.16，拉伸子午面上与压缩子午面上的第二应力不变量之比K=0.667，黏性参数μ=0.005.在中柱顶部建立参考点和刚性耦合面约束，并施加500 mm方向向下的位移荷载，网格单元划分尺寸为30 mm.

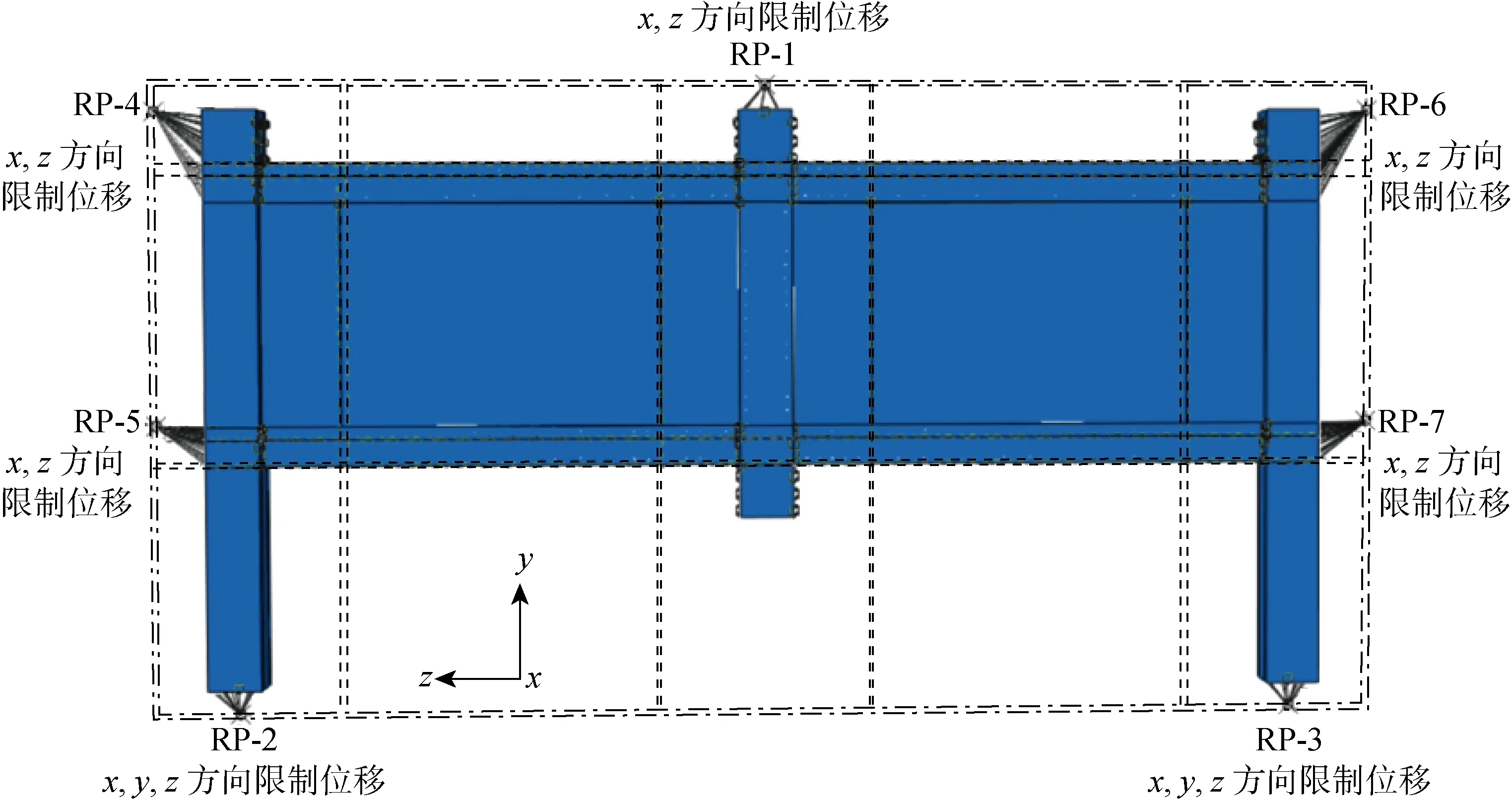
图6 双填充墙预制框架有限元模型Fig.6 An FE model of two-infill wall PC frame

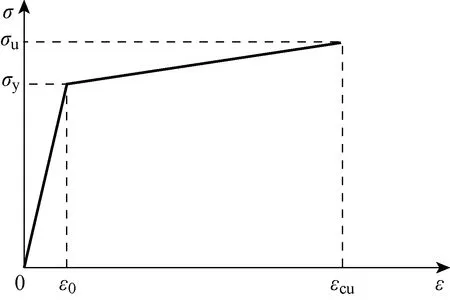
图7 双折线模型Fig.7 Double broken line model

2.2 数值模拟结果

参考已有试验数据建立有限元模型，图8为无填充墙和双填充墙PC框架的试验与有限元法(FEM)数值模拟结果对比.其中，空心圆为梁机制阶段峰值荷载点，实心圆为悬链线机制阶段峰值荷载点.两个框架的梁机制阶段和悬链线阶段所对应的峰值荷载和位移如表2所示.根据试验数据，当荷载达到悬链线阶段峰值荷载后，由于结构损坏，中柱能够承受的荷载急剧下降.在实际情况中，由于顶部荷载不会降低，结构在达到峰值荷载后将会持续损坏至结构倒塌，所以达到悬链阶段峰值荷载时的位移即为连续倒塌的临界位移.在对无填充墙PC框架进行模拟时，由于简化了边界条件，所以初始刚度下降.而在双填充墙PC框架有限元中，试验过程中填充墙与PC框架之间存在一定空隙，因此试验刚度比有限元刚度小.峰值荷载误差小于15%(保守值)，因此有限元模拟可以用于预测结构不同受力机制荷载.

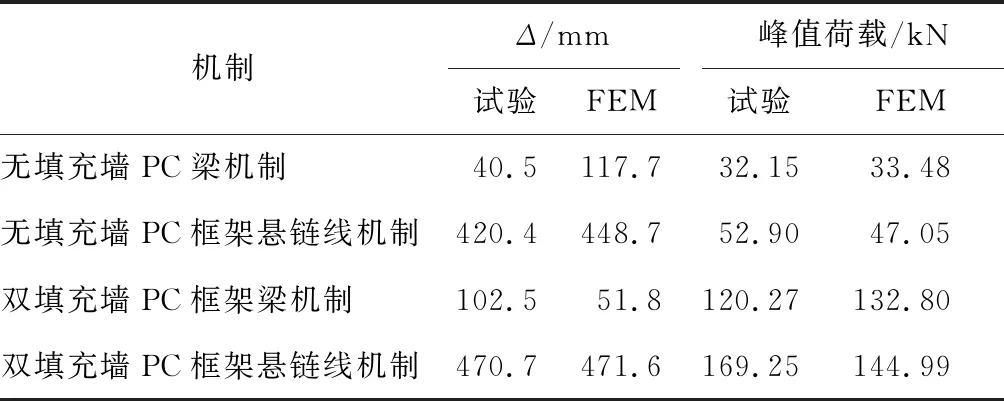
表2 无填充墙和双填充墙PC框架中柱位移-荷载数值

图9为单填充墙PC框架的数值模拟，S表示Mises等效应力.图10为有限元模拟所得单填充墙中柱位移-荷载曲线.图10中，当Δ=81.6 mm时，出现第一个荷载峰值点，此时P=60.567 kN，继续加载时荷载明显减小.当加载至Δ=158 mm时， 悬链线效应开始发挥作用，荷载逐渐增大，并在Δ=496.3 mm时，增至悬链线阶段峰值荷载，此时P=112.629 kN.同时，在单填充墙的情况下，中柱将会受到剪力影响而发生一定的剪切变形，因此在设计中应适当加强柱子的抗剪能力，防止柱子在结构达到悬链线峰值荷载前发生剪切破坏.

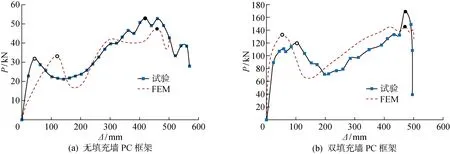
图8 中柱位移-荷载曲线Fig.8 Load-displacement curves of middle column

图10 单填充墙PC框架中柱位移-荷载曲线Fig.10 Load-displacement curve of single-wall PC frame

3 算例

3.1 试验与有限元算例的解析计算

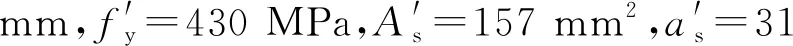
3.1.2无填充墙PC框架悬链线阶段 试验中通长钢筋总长度为 3 920 mm，因此取l1=l2=1 960 mm.该阶段Δ=420.4 mm，计算得到sinγj=0.209 7.由于破坏类型为钢筋滑移破坏，且在梁机制阶段梁内出现塑性铰，钢筋发生屈服，所以fT=430 MPa.根据文献[8]，在进行拉结强度计算时，应该取过中柱的通长钢筋的面积.在此结构中，梁内钢筋直径为10 mm，且只有上部2根钢筋为通长钢筋，因此As=157 mm2.计算得到Pe=4×157 mm2×430 MPa×0.209 7=56.627 kN.试验中，Pe=52.900 kN，相对误差为7.0%.

3.1.3双填充墙梁机制阶段 该阶段Δ=102.5 mm.总抗力由框架和填充墙等效压杆提供的抗力叠加而成.框架提供的抗力Pc=31.134 kN.在计算等效压杆宽度时，tinf=100 mm，Hinf=850 mm，Linf=1 800 mm，σinf=22.19 MPa，柱截面为200 mm×200 mm，梁截面为100 mm×150 mm，Icot=1.3×108mm4，计算得到a=55.28 mm，sinβ=0.383 5.进一步得到Pinf=47.042 kN，双填充墙梁机制阶段峰值荷载Pcw=47.042 kN×2+31.134 kN=125.218 kN.试验中，Pcw=120.270 kN，相对误差为4.1%.

3.1.4双填充墙悬链线机制阶段 该阶段Δ=470.7 mm，sinγj=0.233 5.由于钢筋断裂，因此fT取抗拉强度590 MPa，计算得到Pe=4×157 mm2×590 MPa×0.233 5=86.516 kN.在计算等效压杆宽度时，由于等效压杆为2根，且两端分别与柱和梁接触，所以柱子惯性矩取两者的平均值，即Icot=8.07×107mm4，计算得到a=45.71 mm，sinβ=0.206 2.进一步得到Pinf=20.915 kN.因为将每块填充墙简化为双压杆，所以双填充墙悬链线机制阶段峰值荷载Pew=20.915 kN×4+86.516 kN=170.176 kN.试验中，Pew=169.250 kN，相对误差为0.5%.

3.1.5单填充墙梁机制阶段 该阶段Δ=81.6 mm，Pc=31.134 kN.在计算等效压杆宽度时，取Icot=1.3×108mm4，计算得到a=51.28 mm，sinβ=0.392 6；η=0.74，由于只有一侧有单压杆，所以Pinf=51.28 mm×100 mm×22.19 MPa×0.392 6×0.74=33.059 kN，单填充墙梁机制阶段峰值荷载Pcw1=33.059 kN+31.134 kN=64.193 kN.试验中，Pcw1=60.567 kN，相对误差为6.0%.

3.1.6单填充墙悬链线机制阶段 该阶段Δ=496.3 mm，sinγj=0.245 5；fT取抗拉强度590 MPa，计算得到Pe=4×157 mm2×590 MPa×0.245 5=90.963 kN.等效压杆宽度计算得到a=45.71 mm，sinβ=0.192 8，η=0.62，并得到Pinf=12.125 kN.由于只有一侧有双压杆，所以单填充墙悬链线机制阶段峰值荷载Pew1=12.125 kN×2+90.963 kN=115.213 kN.试验中，Pew1=112.629 kN，相对误差为2.3%.

3.2 按规范取值计算

在悬链线阶段计算拉结力时， 中柱位移为跨度的0.2倍[8].在此案例中，梁跨度为2 m，因此Δ=400 mm.将Δ=400 mm代入式(1)和(11)，计算结果和解析解以及试验有限元解如表3所示.

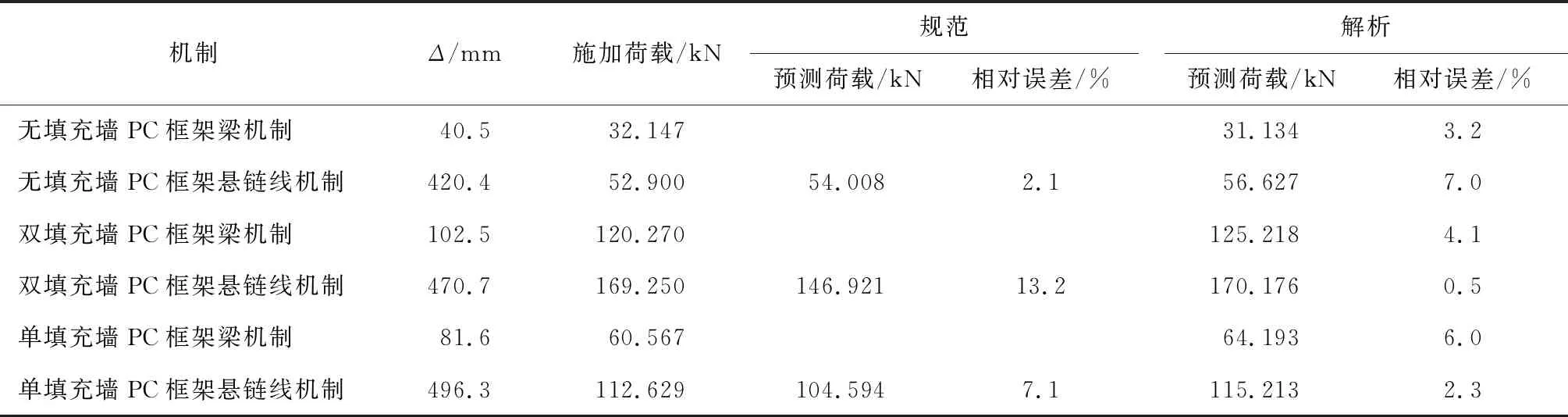
表3 解析与规范推荐方法预测结果Tab.3 Prediction results of analytical approaches and current standard

由计算可知，在悬链线阶段，中柱位移取跨度的0.2倍对于无填充墙PC框架的计算比较准确.但是对于含有填充墙的PC框架计算结果过于保守.主要原因为当装有填充墙时，中柱上的部分荷载可以通过填充墙分散到梁上，而无填充墙PC框架只能通过中柱向梁端点传递集中荷载，因此相对于装有填充墙的PC框架，无填充墙PC框架梁的受力更均匀，框架达到悬链线阶段时的中柱位移更大.

4 结论

(1) 填充墙的不对称分布会导致中柱受到剪力影响，设计过程中应适当加强柱子的抗剪能力，防止结构在进入悬链线机制前发生中柱剪切破坏.

(2) 混凝土填充墙对PC框架结构抗力的提高作用明显.在梁机制阶段，由填充墙不对称分布引起的中柱平面内偏转将会明显削弱单填充墙对结构抗力的贡献.在计算单填充墙荷载时引入不对称系数可以提高计算精度.

(3) 在梁机制阶段，填充墙可简化为单根等效压杆；在悬链线机制阶段，由于填充墙对角发生破坏，其受压区沿对角线向两侧分化，原单杆模型不再适用，应转化为双杆模型.

(4) 在梁机制阶段，规范中中柱位移采用0.2倍跨度的建议对于填充墙PC框架结构过于保守，填充墙可以增大结构到达悬链线阶段峰值荷载时的位移，因此应适当增大建议值.

致谢感谢嘉兴宏业院士工作站对本项目试件连续倒塌试验提供测试方案和设备.