长期受荷桩极限承载力的预测

李镜培, 徐子涵

(同济大学 岩土及地下工程教育部重点实验室；地下建筑与工程系， 上海 200092)

近年来，全国各大城市高速发展，可用于新建建筑的土地资源不断减少.同时，随着城市老旧建筑功能过时，出现了大量需要在建筑原址上进行升级改造的工程.改造工程中如何合理再利用经历长期受荷的旧桩成为一个新的课题[1].

桩基承载能力具有时间效应，随着桩周土体超孔隙水压力的消散[2-3]和土体蠕变[4-5]等因素的影响，长期受荷的旧桩基通常具有比新桩更高的承载能力.这种现象最初于1900年观测到，承载力的增长幅度最多可达沉桩结束时的数倍[6-7].对于静压桩，由于沉桩过程的挤土效应，桩周土体超孔隙水压力的消散会导致桩承载力产生较大幅度的提升.因此旧桩再利用工程中对静压桩的承载能力重新进行评估，可以在保证工程安全性的前提下节省工程预算，具有较大的工程经济价值[8-10].

根据以往的研究结果，已有的一些经验公式可用于既有旧桩承载力的计算评价，但这些经验公式在工程实际应用中还存在适用性较差、计算参数难以确定等问题[11].本文基于现有的经验公式和相关桩基承载力时效性理论解答，通过收集分析美国佛罗里达大学(UF)及路易斯安那州交通研究中心(LTRC)等研究机构对长期受荷桩基承载力的测试研究数据，提出了基于我国现行桩基设计规范，可适用于工程实际的旧桩极限承载力计算公式.对公式中参数取值的问题进行了讨论，并通过国内工程现场试验对本文计算公式的合理性进行了验证.

1 旧桩承载力计算方法探讨

1.1 考虑时间效应的桩基承载力经验公式

国外对桩基承载力时间效应的研究起步较早，积累了大量不同工程地质环境下桩基承载力随时间变化的资料，通过分析数据并加以总结，提出了一些经验公式.

目前国外常用的公式是Skov等[12]所建议的公式，其采用对数时间轴，具体表达式如下：

(1)

式中：Qt为沉桩后t时刻的桩基承载力；Q0为t0时刻的桩基承载力；A为根据土体类型确定的参数；t0为土体超孔隙水压力开始呈线性消散的时刻.

确定Q0与t0通常需要在现场进行载荷试验，也可根据现场数据进行分析或根据当地经验总结得到.影响t0的主要因素为土的类型及桩径等.桩径越大，t0越大，黏性土中一般取t0=1～2 d.参数A取决于土的类型，与桩的埋设深度、超孔隙水压力的消散状况无关.

此外，还有多位学者提出了相关经验公式.Pei等[13]以沉桩结束时刻的桩基承载力QEOD和桩基最大承载力Qmax作为参考承载力，提出如下桩基时效承载力计算公式：

Qt=QEOD+0.263(lgt+1)(Qmax-QEOD)

(2)

Bogard等[14]以桩的最终承载力Qu和沉桩50%所需时间T50作为参考承载力和参考时间，提出如下桩基承载力计算公式：

(3)

上述经验公式具有较大的理论和工程意义，例如都指出了沉桩之后桩基的承载力会随时间增长，且增长速率随时间减小.然而，这些公式大都存在以下缺陷，导致在工程实际中的应用存在局限：

(1) 已有的经验公式主要是对桩基总承载力的增加进行估算，未考虑桩侧阻力与桩端阻力影响的差异，导致上述经验公式仅适用于特定的土性、桩型条件，不同公式的适用范围都较为有限.

(2) 上述经验公式大多需要沉桩结束时刻的承载力作为参考承载力，对于长期受荷的旧桩，由于服役时间已久，这些数据往往难以准确确定.

(3) 这些经验公式多为国外研究成果，与国内现行规范中桩基承载力计算公式缺乏联系，难以在国内工程设计中推广应用.

因此，有必要在考虑桩基承载力时间效应影响因素的条件下，提出更为通用的旧桩承载力计算公式.在满足一定计算精度的前提下，公式中的计算参数应便于选取.同时，计算公式应与现行桩基技术规范的计算方法相结合，方便工程设计人员参考使用.

1.2 考虑时间效应的桩基承载力理论解答

由于通过对现场载荷试验结果进行统计拟合得到的经验计算公式无法从机理上反映桩基承载力时效性的本质，本文依据相关理论研究对桩基承载力时效性的影响因素进行了总结分析.

Li等[15]基于K0固结条件下的修正剑桥模型(K0-MCC)，在综合考虑天然饱和黏土各向异性和应力历史的基础上，基于总应力法推导了天然饱和黏土地层中静压桩时变承载力的解析解，提出了桩侧和桩端承载系数的理论计算方法，进而提出了考虑时效的静压桩极限承载力的理论公式：

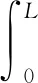
(4)

(5)

(6)

上述理论公式综合考虑了土体原位力学特性、沉桩效应、桩端土再固结过程，在计算出桩侧承载系数和桩端承载系数后，可采用三轴条件下土体的原位不排水抗剪强度直接计算任意时刻静压桩的极限承载力.Li等[15]通过对α1(t)和α2(t)进行理论计算，认为沉桩结束后桩侧承载系数随再固结时间的增幅远高于桩端承载系数，沉桩结束后桩承载力的增长主要是桩侧承载力的增长.基于该理论，本文计算对静压桩承载力时间效应的影响因素进行了简化，仅考虑桩侧承载能力提高对旧桩承载力的影响.

2 旧桩极限承载力标准值计算方法

基于上述理论研究结果，结合经典桩基承载力时效经验公式，本文提出了可与现行规范相结合的长期受荷旧桩极限承载力标准值计算方法.

2.1 旧桩极限承载力标准值计算公式

文献[16]中规定，当根据土的物理指标和承载力参数之间的经验关系确定单桩极限承载力标准值时，宜按下式计算：

Quk=Qsk+Qpk=u∑qsikli+qpkAp

(7)

式中：Quk为单桩极限承载力标准值；Qsk、Qpk分别为总极限侧阻力标准值和总极限桩端阻力标准值；u为桩身周长；qsik为桩侧第i层土的极限侧阻力标准值；li为桩周第i层土的厚度；qpk为极限端阻力标准值；Ap为桩端面积.

式(7)将单桩极限承载力分为了桩侧和桩端两部分.本文提出桩侧阻力时效系数γ，以式γu∑qsikli表示考虑时效性的桩侧阻力，通过γ取值与沉桩过后时间之间的关系，反映桩侧桩基承载力随时间的改变量，进而提出考虑时效性的静压桩极限承载力标准值计算公式：

Quk=Qsk+Qpk=γu∑qsikli+qpkAp

(8)

γ的确定方法将在下文讨论.

式(8)与现行单桩极限承载力标准值计算公式(7)之间仅有一个参数γ的区别，便于工程应用.该式仅对桩侧阻力进行修正，在γ取值合理的情况下，相对于其他经验公式，更为明确地反映了静压桩承载力的时效特征.

2.2 考虑时效性的桩侧阻力计算

为了合理预测桩侧阻力随时间的增长，本文采用佛罗里达大学在5处沿海土壤中沉桩，并观测5年的试验数据[17]，对不同场地、不同土层条件下桩基的桩侧阻力随时间的变化关系进行了统计分析.

图1为5个场地桩侧阻力Qs与沉桩时间t的关系，其中时间采用对数坐标.从图中可以看出，沉桩一段时间之后，所有桩基的侧阻力几乎都与时间对数成线性关系，以γs表示沉桩后任意时刻桩侧阻力与初始时刻桩侧阻力的比值，则γs可采用下式表示：

(9)

式中：B和C为实测数据拟合得到的参数；t0为超孔隙水压力开始呈线性消散的时刻，依据Skov等[12]的相关理论，取t0=1～2 d.

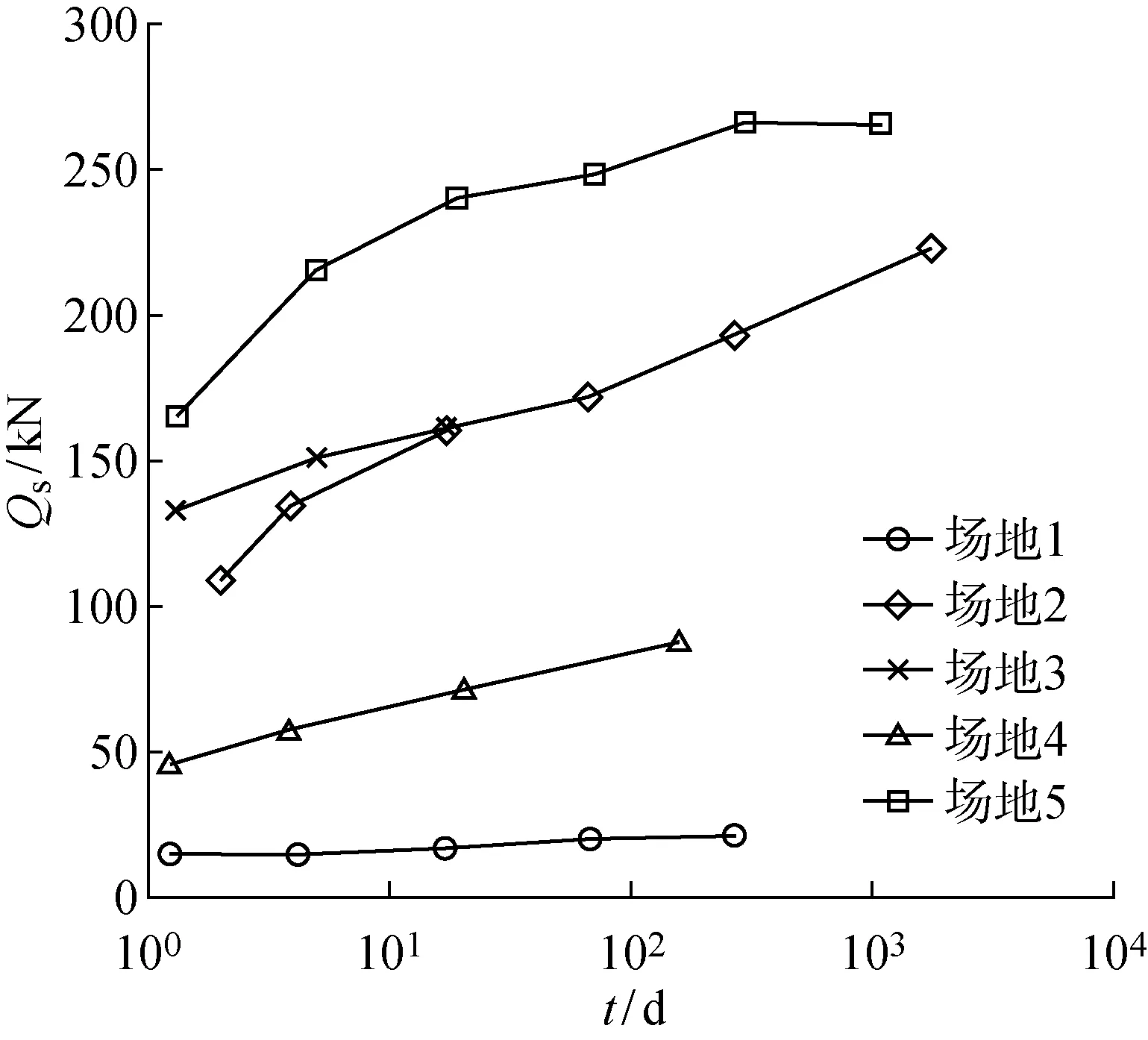
图1 桩侧阻力与沉桩时间关系曲线Fig.1 Correlation of pile side resistance versus time

为确定参数B和C，计算各场地不同时刻的γs，得到γs与lg(t/t0) 的关系，如图2所示.从图中可以看到，不同场地桩侧阻力时效系数随时间线性关系的截距差异较小，且当t/t0>1时，γs>1.0，表明沉桩结束后桩侧阻力均随时间增长.对各条曲线进行拟合，获得直线斜率为B，截距为C.其中B的取值为0.17～0.35，C的取值为0.92～1.1，拟合优度决定系数R2为0.88～0.96.

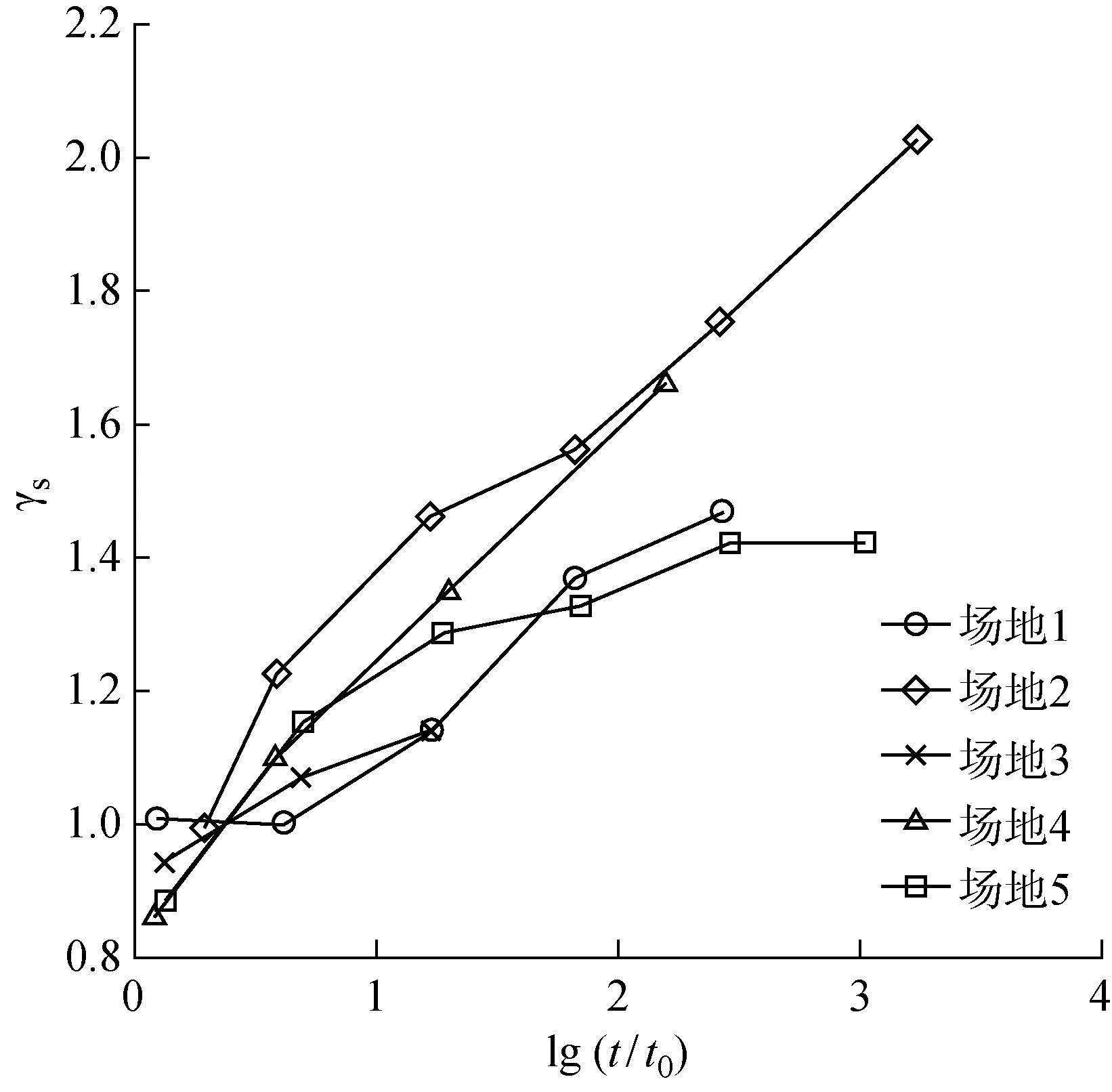
图2 γs与lg (t/t0)关系Fig.2 Correlation of γs versus lg (t/t0)

取C的值为1，B是一个与场地条件相关的参数，对于场地资料缺少的静压桩，本文认为B可取保守值0.17，则：

(10)

2.3 桩侧阻力时效系数的计算

值得注意的是，γs表示的是桩侧阻力相对于超孔隙水压力开始呈线性消散时刻的承载力的增长.这一时刻桩的极限承载力往往还达不到现行规范计算得到的单桩极限承载力.为确定γ，应确定单桩极限承载力的参考时间.文献[18]中规定，根据土体类别的差异，沉桩之后，桩承载力监测前应有休止时间，如表1所示.

表1 桩基承载力监测休止时间Tab.1 Rest time of pile bearing capacity test monitoring

以休止时间作为规范计算的极限承载力的参考时间，以该时刻的桩侧阻力作为参考承载力.因此，结合式(9)，γ可表示为

(11)

式中：t1为旧桩所在场地的桩基承载力检测休止时间，按表1取值.

根据本文采用试验数据，当B值取0.17时，对于沉桩时间达数年以上的静压桩，计算得到的γ偏于安全，可用于评估长期受荷的静压桩的承载能力，并用于相关桩基工程初步设计.γ值与场地土条件有关，对于具体的工程场地，其更为合理的取值需要根据场地土相关参数进行计算确定.

3 时效系数γ参数取值方法

式(11)中B值是决定γ大小的关键参数，该值与土体性质紧密相关.对于多层土场地，可确定各土层的B值，再根据土层厚度进行加权平均即可得到整个场地的平均B值.

本文采用佛罗里达大学和路易斯安那州交通研究中心分别进行的现场载荷试验所得到的数据[17,19-21]，对不同工程场地的67层黏土层的B值与土层各项参数之间的关系进行了统计分析，结果表明：B值随土体不排水抗剪强度Su的增大而减小，随土体塑性指数IP的增大而增大.

图3 B值与不排水抗剪强度Su的拟合关系Fig.3 Correlation of B versus undrained shear strength Su

3.1 不排水抗剪强度Su的影响

Li等[15]认为采用土体的原位不排水抗剪强度可以直接计算旧桩的极限承载力，因此首先考虑不排水抗剪强度Su与B值的关系.各试验场地土层不排水抗剪强度Su从5～156 kPa不等，图3为试验场地不同土层的测试数据换算得到的参数B与Su的关系.从图中可以看出，B值与Su为负相关关系，即在Su较小的软黏土当中，参数B较大，桩基承载力随时间对数的增长率较大；在Su较大的硬黏土当中，参数B较小，桩基承载力随时间的增长率较小.

直接对B-Su关系进行线性拟合，R2为0.594，表明B与Su的线性相关度较差.对B-Su关系采用指数函数进行非线性拟合，如图3所示，R2为0.754，拟合优度较高，且高于采用对数函数拟合(R2=0.68)以及采用幂函数拟合(R2=0.66)的结果，因此本文认为可采用以下指数函数形式计算B值：

B=0.5e-0.009Su

(12)

3.2 塑性指数IP的影响

土体塑性指数IP是描述场地土性质的重要参数.Ksaibati等[7]认为土体塑性可以反映土体的时效强化，Haque等[22]认为可采用塑性指数对桩侧摩阻力的时效增长预测.因此，本文亦对土体塑性指数IP与B的关系进行了统计分析.试验场地各土层的塑性指数IP从5%至81%不等.图4为不同土层B值与IP之间的关系，从中可以看出，B与IP为正相关关系.

图4 B值与塑性指数IP的拟合关系Fig.4 Correlation of B versus plasticity index IP

对B与IP进行线性拟合，R2为0.734，线性相关度较好.因此，本文认为亦可采用IP作为计算B值的土性参数，建议采用下式计算B值：

B=0.005IP+0.1

(13)

采用上述计算方法，可以针对具体的工程场地按式(12)或(13)计算其土层的B值，进而根据式(11)计算得到场地的γ，计算结果具有较好的可信度.如场地资料允许，可分别采用两种参数计算B值，取其γ较小值用于场地土桩基承载力评价.

4 工程验证与分析

4.1 现场试验概况

试验场地位于上海浦东新区周浦镇周东路西侧，地貌类型属滨海平原，地貌形态单一，土层平均厚度H、土体容重γ、孔隙比e、黏聚力c、内摩擦角φ及压缩模量Es等物理力学性质资料见表2.

对场地原有的3根桩龄30 a的旧桩以及打入28 d的3根新桩进行单桩竖向静载荷试验.加载方式为慢速维持荷载.旧桩桩径400 mm，桩长30 m，每级加载量为180 kN.新桩桩径300 mm，桩长29 m，每级加载量为105 kN.

表2 试验场地土层物理力学性质

4.2 试验结果对比分析

根据式(12)，对该场地桩长范围内的土层进行计算，得到B=0.22，再结合式(11)和(8)计算得到该试验旧桩、新桩的极限承载力预测曲线.试验测得3根旧桩和3根新桩的极限承载力Q后，将该实测值与根据本文方法计算得到的旧桩、新桩极限承载力预测曲线对比，如图5所示.

图5 新、旧桩极限承载力预测曲线和实测值Fig.5 Prediction curves and measured values of ultimate bearing capacity of new and old piles

从图5可以看出，对于桩龄长达30 a的3根旧桩，试验得到的极限承载力实测值分别为 2 340 kN、2 160 kN、2 160 kN，平均值为2 220 kN.按照本文方法计算得到的极限承载力预测值为 2 063 kN，与旧桩试验承载力平均值接近，表明本文方法能够较为合理地预测长期受荷旧桩的极限承载力.

对于沉桩时间为28 d的3根新桩，试验得到的极限承载力实测值分别为 1 260 kN、1 365 kN、1 210 kN，平均值为 1 278 kN.按照本文方法计算得到的极限承载力预测值为 1 023 kN，二者有一些差异，说明采用本文方法预测桩的短期承载力方面还存在一定误差.但该误差值在20%以内，且预测值偏小即偏于安全，因此本文计算方法亦可用于对沉桩一段时间之后的新桩极限承载力变化进行预估评价.

5 结论

本文通过总结修正已有桩基础时效承载力经验公式，结合静压桩承载力的时效性研究的理论成果，分析处理已有相关载荷试验结果，得到了以下主要结论：

(1) 在现行《建筑桩基技术规范》中单桩极限承载力计算方法的基础上提出了桩侧阻力时效系数γ的概念，进而提出了考虑桩基承载力时效性的静压桩极限承载力计算方法，并给出桩侧阻力时效系数γ的计算公式.

(2)γ的计算公式中，参数B与土体性质相关.试验结果统计表明，B值随土体不排水抗剪强度Su的增大而减小，随土体塑性指数IP的增大而增大.在以黏土为主的场地中，提出了根据土性参数计算B值的公式.

(3) 通过与工程现场试验结果的对比，本文提出的考虑桩基承载力时间效应的旧桩极限承载力计算方法能够较为合理地预测旧桩的极限承载力，该值可用于评估长期受荷的静压桩承载力随时间的增加量，对解决旧桩再利用工程中承载力计算问题具有一定的参考意义.