方柱跨声速流动中的剪切层和尾迹特性
许常悦,郑 静,王 哲,王 彬
(南京航空航天大学 飞行器环境控制与生命保障工业和信息化部重点实验室, 南京 210016)
在工程中,人们会经常遇到各类复杂流动现象,如附体边界层流动、大范围分离流、分离剪切层、湍流旋涡及尾迹等.钝体绕流中包含这些复杂流动特征,具有较好的代表性,进而引起人们的关注.根据边界层分离位置的不同,钝体可以分为两类:一是具有移动分离位置;二是固定分离位置.在具有移动分离位置的钝体中,圆柱属于典型的规范构型,相关研究较多,包括不可压流和可压缩流动[1-3].另一种具有固定分离位置的钝体规范构型是方柱.近年来,方柱不可压绕流的研究报道较多[4-10],然而缺乏关于可压缩流动的研究.
由于方柱不可压绕流具有丰富的实验和数值数据,故人们常把该流动问题选为新方法的验证算例.例如,Murakami等[4]针对雷诺数Re=22 000 的方柱不可压绕流开展大涡模拟(LES)研究,评估了几种亚格子模型对计算结果的影响.结果表明,基于Lagrange型动力学模型的计算结果与实验数据吻合最好.邓小兵等[5]以方柱不可压绕流为研究对象,利用基于虚拟压缩的LES方法进行计算,并与实验数据进行对比,验证了该方法的可行性.唐鹏等[6]利用两类RANS/LES(RANS为雷诺平均Navier-Stokes)混合方法模拟了Re=22 000 的方柱不可压绕流,通过与实验数据进行对比,对混合方法的预测性能进行了评估.Minguez等[7]运用高阶LES方法和实验手段对Re=21 400 的方柱不可压绕流进行深入研究.他们给出了丰富的定量数据,便于其他研究者用于新方法的广泛验证工作.他们还探讨了卡门涡街与自由剪切层Kelvin-Helmholtz (K-H)不稳定性的关系.Trias等[8]采用直接数值模拟(DNS)方法对Re=22 000 的方柱不可压绕流进行精细模拟.DNS结果与已有实验数据吻合较好,能够捕捉近壁面区域的转捩现象.Bai等[9]利用LES和分离涡模拟(DES)方法对中等雷诺数下的方柱不可压绕流进行模拟.与实验数据进行对比发现,DES模型的预测性能优于传统的LES和RANS模型.李真子等[10]采用自主发展的LES程序对Re=22 000 的方柱绕流进行精细模拟,并与DNS结果和实验数据进行对比,验证了LES方法的可靠性.
目前,关于方柱可压缩绕流的文献较少,且以实验研究为主.例如,Nakagawa[11]在跨声速风洞中对不同雷诺数和不同来流马赫数(Ma)的方柱流场进行了测量.雷诺数和来流马赫数分别为0.696×105 从上述研究可以看出,LES方法适用于研究方柱绕流问题.然而,为了使LES方法准确地捕捉湍流边界层,壁面附近仍需较密的网格.为了进一步减少计算代价,人们构造了多种RANS/LES混合方法,其中以DES方法的应用最为广泛.然而,早期的DES方法存在RANS和LES计算区域模糊问题,即所谓的“灰区”问题.不合适的网格设计,将会导致网格诱导分离现象.人们针对早期DES的不足,提出了各种改进策略,如延迟分离DES(DDES)方法[16]及改进的延迟分离DES(IDDES)方法[17]等.针对某些特定问题,这些改进策略取得了一些成功的计算结果.然而,DDES和IDDES会引入额外的经验参数,且会增加额外的计算量,这违背了DES发展的初衷.另外一种能够实现RANS/LES混合计算效果的方法是尺度自适应模拟(SAS)方法.目前,应用较多的是Menter等[18-19]发展的两方程SAS方法.我们曾发展了一种一方程SAS方法[20-21],具有计算量小且预测性能好的优点.本文将利用该SAS方法作为数值计算工具,进一步评估该方法的预测能力,这也是本文的另一个研究目的. (3) (4) (5) 式中:μT为湍流黏性系数,需要通过构造尺度自适应模型进行求解;Sij=0.5(∂ui/∂xj+∂uj/∂xi)为速度应变率张量,根据张量符号运算规则,Skk=S11+S22+S33;PrT为湍流普朗特数,常近似取值0.92.为了构造一方程的尺度自适应模型,需要对Spalart-Allmaras (SA)湍流模型方程进行修改.SA湍流模型输运方程可以写成如下形式: {Cb1[(1-ft2)fv2+ft2]/κ2-Cw1fw} (6) (7) (8) (9) (10) 当d>Lvk/κ时,SAS执行类LES计算;当d SAS的控制方程采用基于结构网格的有限体积方法进行求解.时间推进采用近似因子分解(AF)方法.为了保证时间的二阶精度,在AF方法中引入带子迭代的伪时间项.空间项的离散按照黏性项和对流项分别进行处理.黏性项采用传统的二阶精度中心格式进行离散.考虑到方柱跨声速流场中会出现激波和湍流共存现象,对流项的离散格式需要同时满足捕捉激波和湍流的要求:利用高耗散的格式(如迎风格式)捕捉激波.湍流捕捉则采用低耗散格式,如中心格式.我们曾基于Roe通量差分裂格式发展了一类中心/迎风混合格式[22],中心和迎风格式可以通过一个二进制开关函数进行自动切换.该数值策略已被成功应用于多种可压缩湍流的数值研究,如钝柱体跨超声速绕流[3, 22-23]、翼型跨声速绕流[24]及超声速的底部流动[21]等.因此,我们有理由认为该数值策略能够用于研究当前问题. 方柱的来流参数依据已有实验[13]进行选取,来流马赫数和基于方柱边长D的雷诺数分别为0.71和4×105.计算采用O型网格,并在近尾迹区和近壁处进行网格的局部加密处理.O型计算域的直径为50D,方柱的展向宽度为4D.为了评估网格分辨率对计算结果的影响,本文计算采用两套网格:径向网格数×周向网格数×展向网格数为197×257×81(网格1)和321×321×121(网格2).图1给出了网格2在方柱横截面的网格分布.两套网格的径向第一层网格厚度均为10-5D,对应的利用壁面单位归一化的网格间距值小于1,符合SAS模拟边界层的要求.在程序中,基于网格1和网格2的计算时间步长分别为0.002D/U∞和0.001D/U∞(U∞为来流速度).为便于表述,基于网格1和网格2的SAS结果分别记为SAS-1和SAS-2.在本文的后处理数据中,符号〈 〉用于表示经过时间和展向平均的物理量. 图1 方柱的O型计算网格Fig.1 O-type computational mesh of square cylinder 表1和图2给出了一些定量数据的比较,表中EXP-1和EXP-2分别为来自Layukallo等[13]和Nakagawa[11]的实验数据.表1中〈CD〉为平均阻力系数,CLrms为升力系数的均方根.图2中A和D分别为方柱前边和后边的中心点,B和C分别为方柱的两个拐点,〈Cp〉为平均压力系数,xs为壁面任意点距A点处的距离.可以看出,SAS-1和SAS-2的结果相差较小,可以认为当前计算满足网格无关性的要求.然而,为了更好地捕捉精细的小尺度流动结构,本文所讨论和分析的数据为SAS-2结果.从表1中可以看出,SAS预测的平均阻力系数略低于实验值EXP-1和LES结果.涡脱落的Sr位于实验EXP-2的可信范围内.从图2中可以看出,在流动分离前,SAS结果与实验数据EXP-1及LES结果均吻合较好;在流动分离后,SAS的预测结果略高于实验数据EXP-1和LES结果.对于钝体跨声速流动而言,实验测量值常存在一定幅度的波动[2],尤其是壁面物理量的测量.本文的SAS结果与实验数据及LES结果较为接近,可认为当前SAS方法具有较好的可靠性. 表1 一些物理量的对比Tab.1 Comparisons of some physical quantities 图2 沿柱体表面的平均压力系数Fig.2 Distributions of mean pressure coefficient on cylinder surface 考虑到流场的快速演化,计算程序选取自由来流参数作为初始条件.为了避免非物理波对流场信息的污染,远场采用基于一维Riemann不变量的无反射边界条件.壁面速度取无滑移、无穿透条件.壁面温度取绝热条件.柱体展向采用周期性边界条件.为了提高计算效率,程序采用分块并行计算:周向分为8块,展向分为3块,共计24块. 图3(a)、3(b)分别给出了利用平均和瞬态当地马赫数展示的方柱跨声速流动形态,图中ωyD/U∞为展向涡量分量,P1~P4表示4个探测点,坐标分别为: P1(-0.055 6, 0.571),P2(0.721, 0.254),P3(1.997, 1.485),P4(-0.214, 0.948).后文将对这4个探测点处的压力信号进行分析与讨论.与圆柱绕流类似,方柱的尾迹区会形成明显的回流区,并有大尺度的涡脱落现象.与圆柱不同的是,方柱前缘拐点处会强迫流动发生分离,进而在剪切层与柱体侧壁之间形成回流区.可压缩效应对流场存在明显的影响,方柱两侧出现大范围的局部超声速区,且在剪切层下游形成运动的激波结构[15].此外,尾迹中也存在局部超声速区.然而,与圆柱跨声速绕流[3,22]不同的是,方柱的分离点处未形成激波,这意味着方柱剪切层下游的压缩波未能向分离点处汇聚. 图3 方柱流动形态Fig.3 Flow pattern of square cylinder 对于钝体绕流而言,其尾迹特性与剪切层的演化行为密切相关.在可压缩流动中,剪切层中的对流马赫数Mc分布常用于分析剪切层的失稳过程[25],Mc的定义为Mc=(〈u〉1-〈u〉2)/(a1+a2),下标1和2分别表示剪切层两侧的高速和低速流动,〈u〉 和a分别为平均的流向速度和当地音速.剪切层的增长可以用剪切层的涡量厚度δω描述,δω的定义为δω=(〈u〉1-〈u〉2)/(∂〈u〉/∂z)max. 图4 剪切层的Mc和δω沿流向分布Fig.4 Streamwise distributions of Mc and δω inside shear layer 图5 斜压项展向分量Fig.5 Isosurface of spanwise component of baroclinic term 图6 不同截面处的Lamb矢量散度云图Fig.6 Contours of Lamb vector divergence at different sectional planes 图7 利用Q准则绘制的三维涡结构Fig.7 Three-dimensional vortex structures plotted by Q-criterion 为了展示尾迹中的大尺度涡脱落现象,图7给出了利用Q准则绘制的三维瞬态涡结构.在剪切层初始发展阶段,剪切层中的涡量分布较为均匀,这与剪切层中的涡量厚度增长较慢有关(见图4).随着剪切层向下游继续增长直至失稳,尾迹中出现大尺度的发卡涡和条状涡结构.从图7可以看出,大尺度涡脱落区的流动速度仍以亚声速为主. 方柱中激波运动、剪切层失稳及涡脱落均会使流场信息发生规律变化.为了获取相关的特征频率,我们在方柱的关键位置布置了4个探测点,如图3(a)所示.借助功率谱密度(PSD)分析,可以获得这4个探测点处压力信号的特征频率,如图8所示,图中k为斜率.PSD曲线的峰值对应流动的特征频率,Sr≈0.135属于柱体的涡脱落特征频率,而Sr≈0.27则是涡脱落特征频率的倍频.图8(a)中PSD曲线高频区呈现 -2 次方斜率关系,这与柱体侧壁与剪切层之间的回流区存在流动再附现象有关[15, 28].图8(b)、8(c)中PSD曲线的高频区呈现 -5/3 次方斜率关系,这说明SAS方法能够模拟湍流的惯性子区[28],进一步验证了SAS方法的可靠性.图8(d)中PSD曲线的高频区未存在快速衰减,这与P4点处的流动仍以层流流动为主有关.图8(a)、8(b) 和8(d)中的PSD曲线出现了明显的倍频关系,甚至3倍频关系,这与剪切层中存在的涡合并现象有关[29].同时,这也说明剪切层中的涡合并现象会导致流场中出现向周围传播的压缩波,进而使得剪切层外侧附近流场和剪切层内侧的回流区受到影响.然而,图8(c)中则未出现倍频关系.从图3(a)可以看出,P3探测点位于方柱外侧局部超声速区的下游,这说明剪切层激发的压缩波未能穿透该局部超声速区向下游传播. 在方柱剪切层的失稳过程中,剪切层中发生涡合并现象,导致激发的压缩波向外传播,剪切层的失稳导致尾迹中出现大尺度的涡脱落现象.可以看出,剪切层的失稳行为直接影响方柱可压缩流动的模态.为了分析方柱可压缩剪切层的失稳对流动模态的影响,借助本征正交分解(POD)技术对方柱的压力场进行分解.关于POD技术的完整描述可以参考文献[30],这里仅对POD的定义作简单说明.对于一个待分解的物理量f(x,t),POD分析可以确定若干正交函数φj(x),j=1, 2,….该物理量f(x,t)在前n个函数上的投影可以写成如下形式: (11) 图8 4个探测点处的压力信号PSD曲线Fig.8 PSD curves of pressure signals at four probes 图9 压力场的前两个POD模态 Fig.9 First two POD modes for pressure field 当前工作采用SAS方法研究了来流马赫数为0.71、雷诺数为4×105的方柱跨声速绕流问题.通过对计算结果进行分析与讨论,可以得到如下的研究结论: (1) 通过与LES结果和实验数据进行对比,可以看出当前SAS方法具有较好的可靠性,能够较好地模拟具有固定分离点的钝体可压缩绕流问题. (2) 方柱剪切层中的对流马赫数约为0.6,这意味着Kelvin-Helmholtz不稳定性主导分离剪切层的演化过程.在剪切层的初始阶段,剪切层中的扰动涡展向呈现滚筒状;Lamb矢量散度呈现负值包裹正值的“夹心三层”结构,抑制了涡量厚度的增长. (3) 通过对方柱流场中布置一些压力信号探测点,借助功率谱密度分析方法,发现剪切层外侧附近和方柱的回流区均出现倍频现象,这与剪切层中存在明显的涡合并现象有关. (4) 压力场的POD分析表明,方柱跨声速流场中的主导流动模态为反对称模态,这与尾迹中的涡脱落现象和剪切层激发的压缩波传播有关.1 数值计算方法
1.1 控制方程
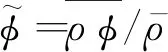

1.2 尺度自适应模型
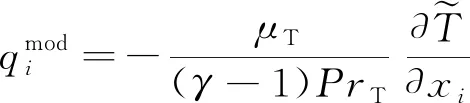

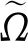


1.3 离散格式
2 计算结果分析与讨论
2.1 计算细节及计算验证
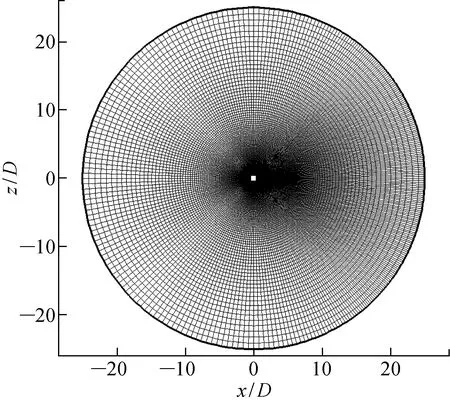
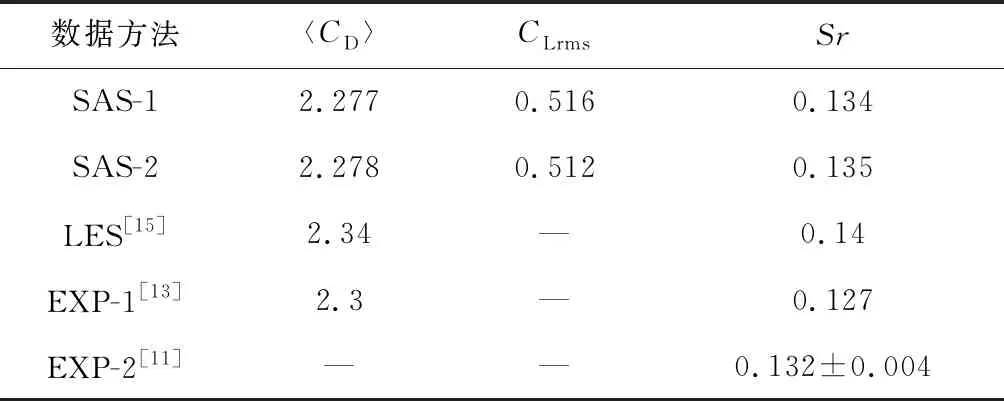
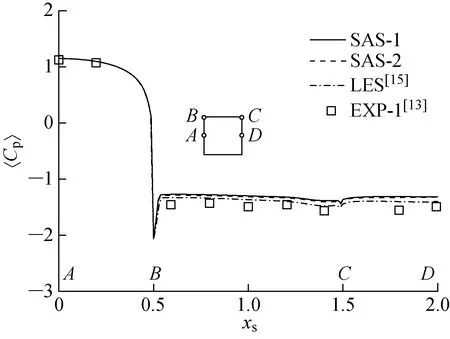
2.2 计算结果
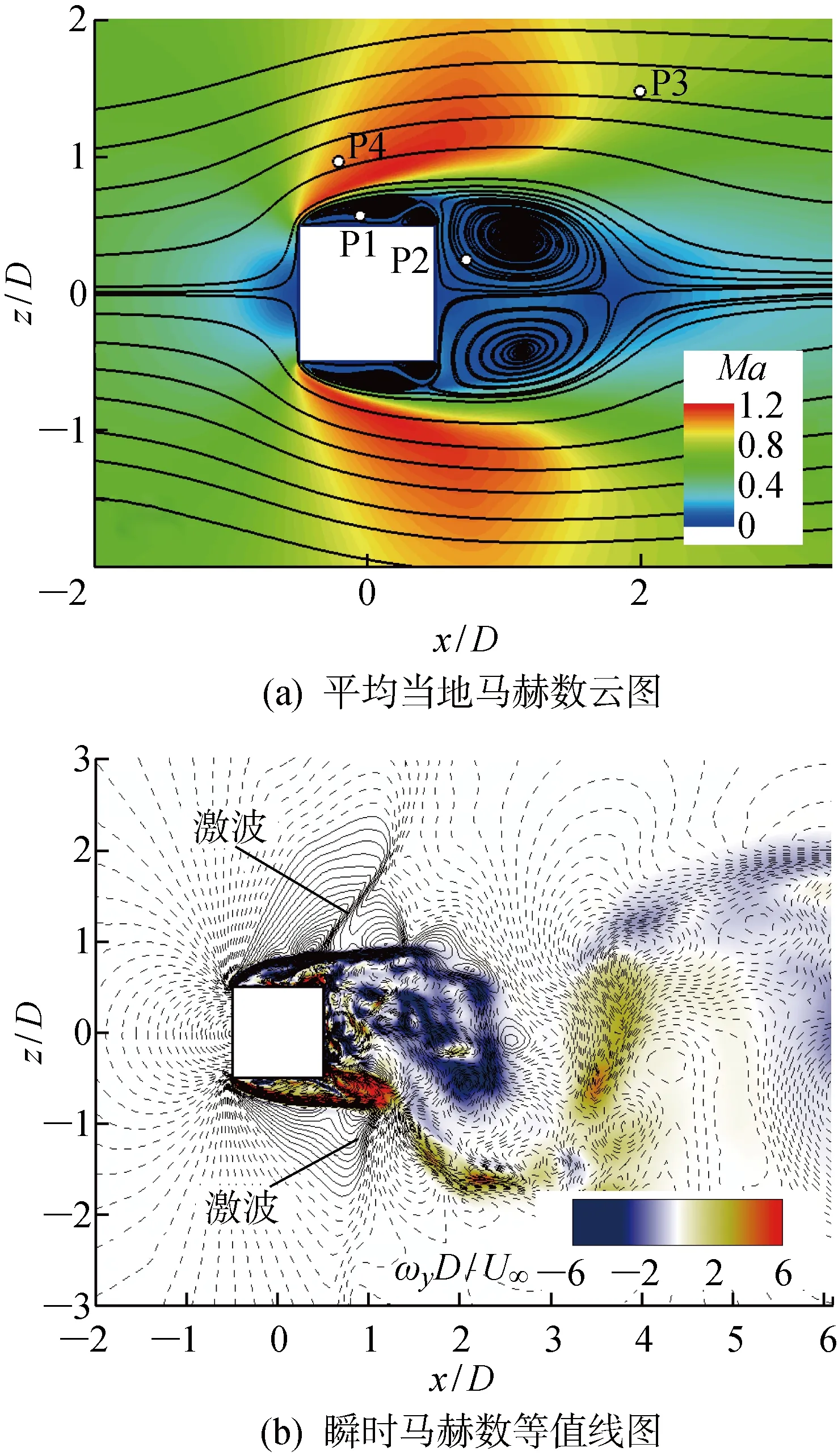

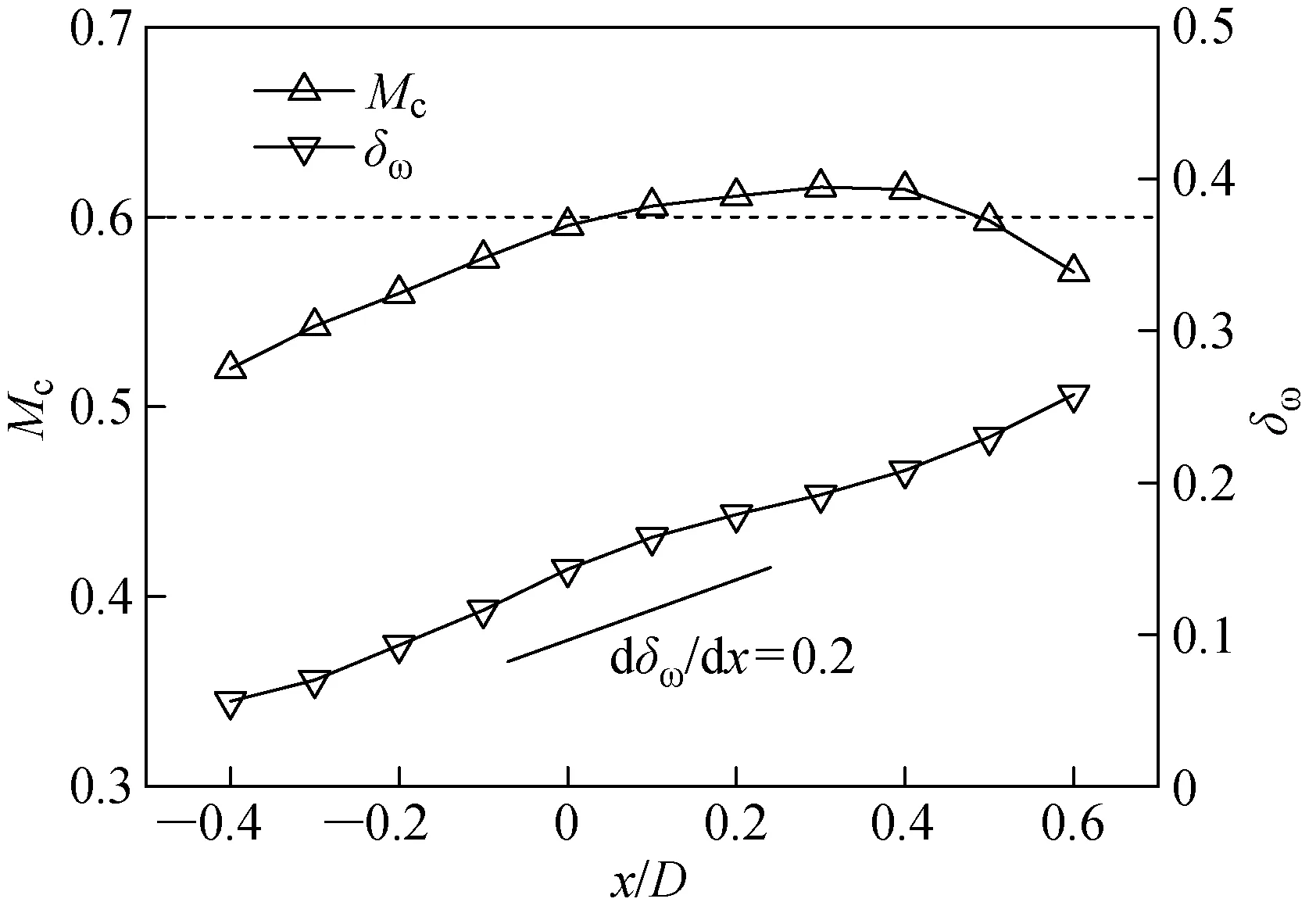
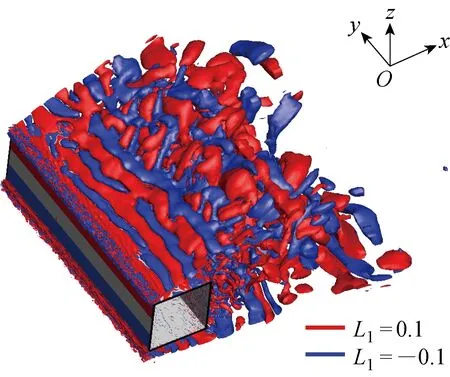

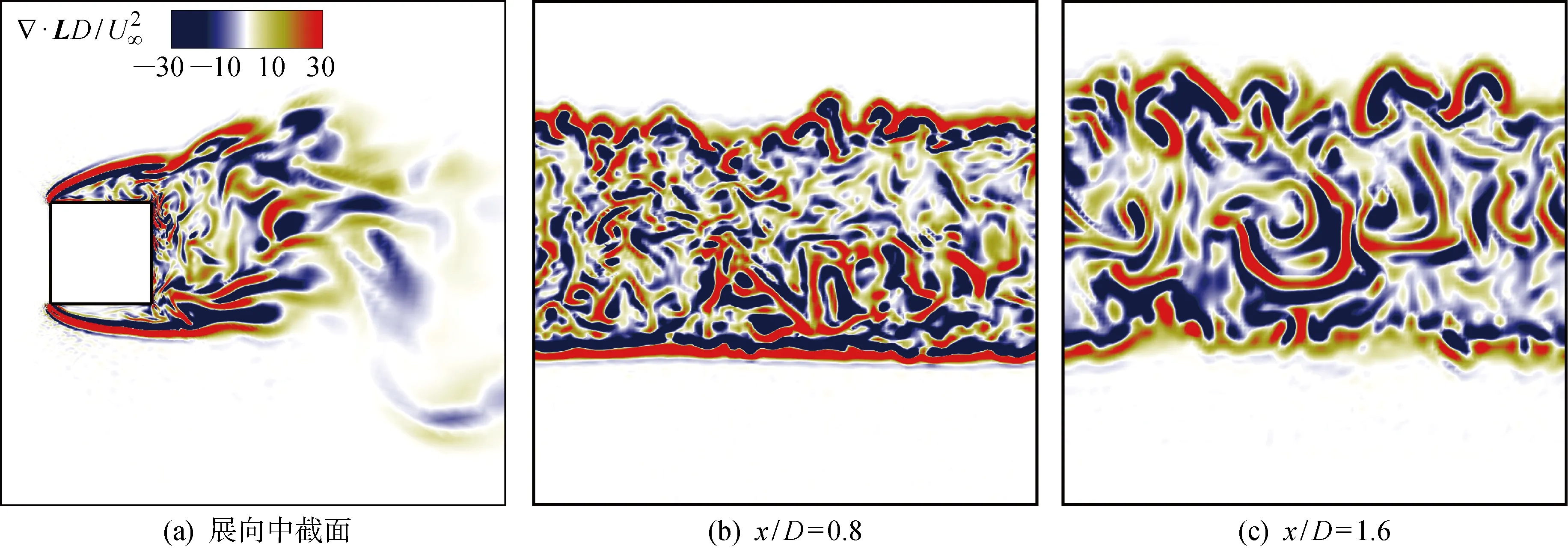
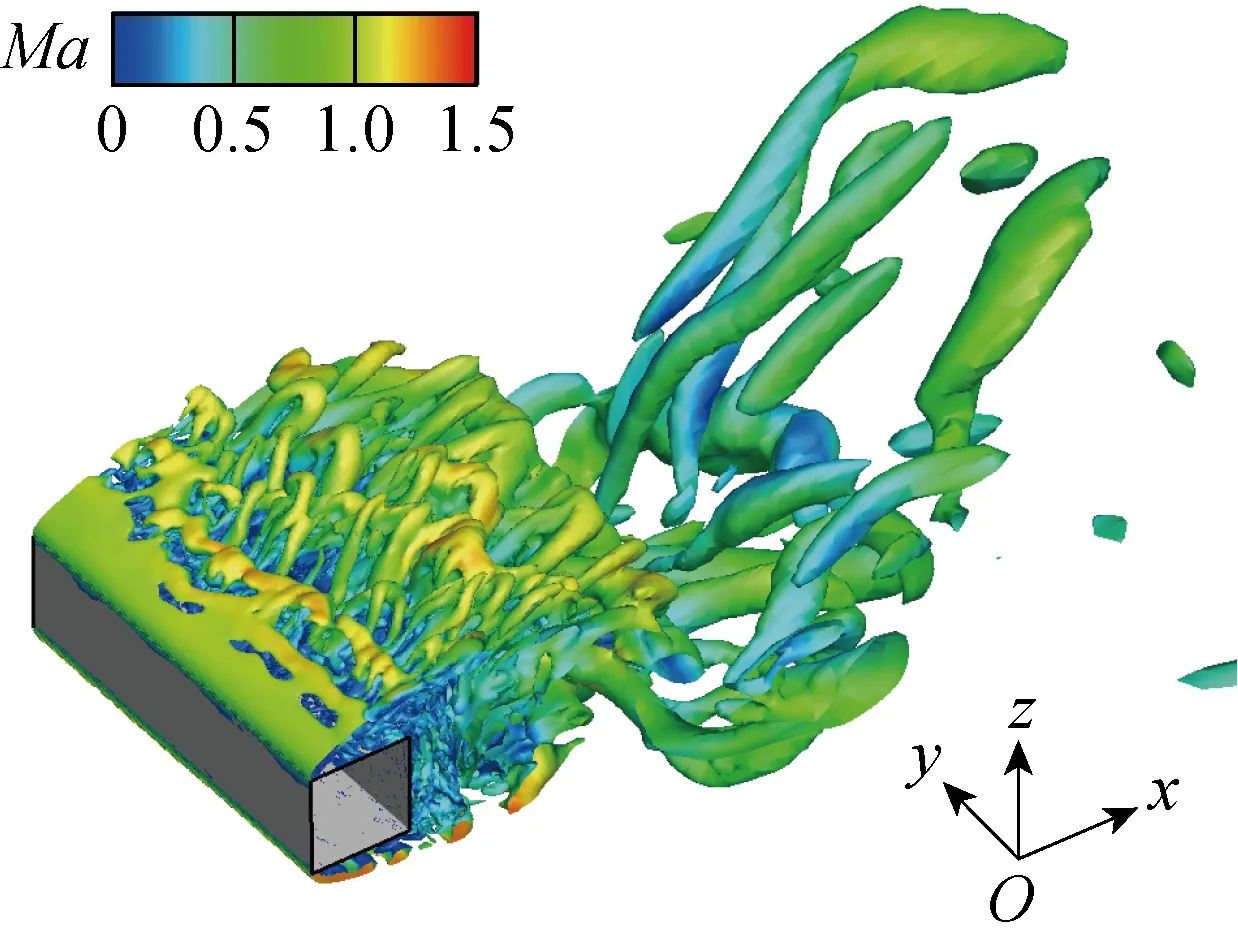


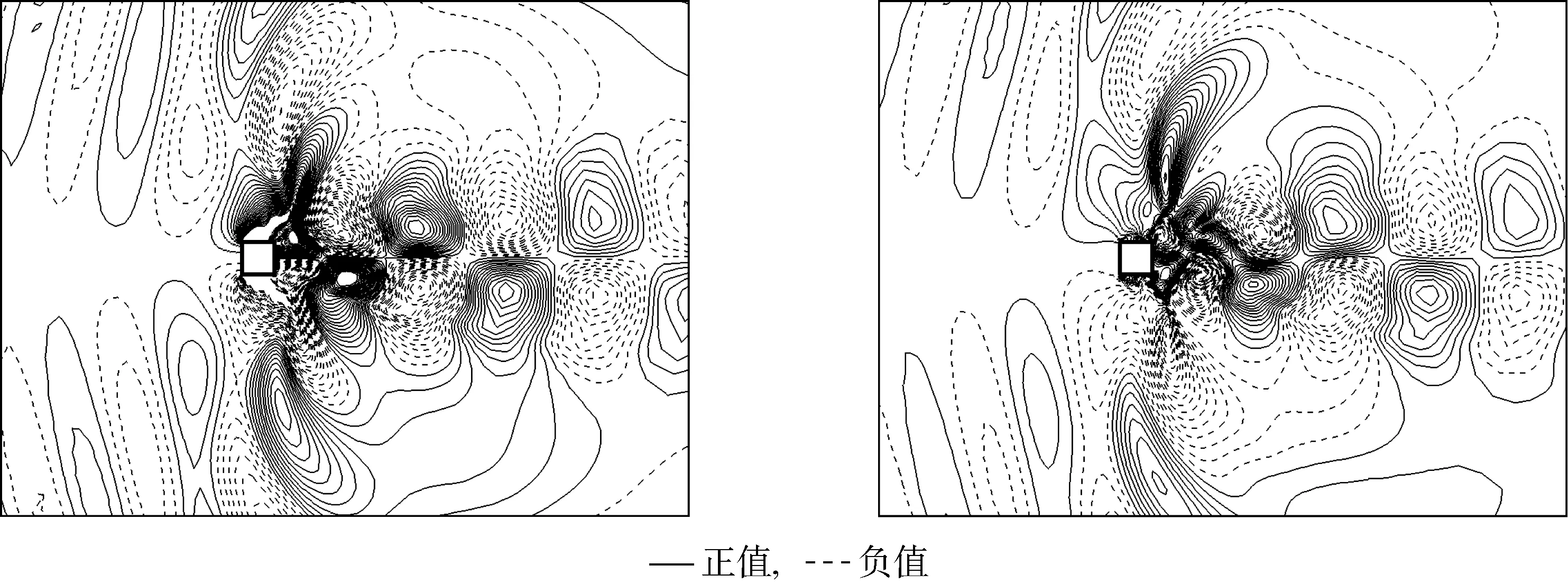
3 结论

