基于马尔科夫决策过程的带缓存双机系统不完美维护策略
田雪雁,王孟雅,潘尔顺
(上海交通大学 机械与动力工程学院, 上海 200240)
设备性能随使用时间退化,发生故障的概率增加,合理预防性维护能够有效提高设备的可用度.但进行预防性维护需要停机,而生产线设备间的退化状态不同,单台设备维护或故障都会造成产线停运.因此,常在设备间设置缓存区,以避免设备维护或故障时频繁中断生产过程.缓存的设置会影响原有的设备维护体系,而现有系统的预防性维护多凭经验决策,故有必要对带缓存生产系统的预防性维护策略的机理进行研究.
从20世纪60年代起,有学者开始关注设备维护优化问题,取得了较好的研究成果[1-5].但针对带缓存生产系统维护策略的研究相对较少.Rezg等[6]研究了生产线的预防性维护和缓存控制,设备到达维护年龄或出现故障立即维护,通过联合优化维护年龄和缓存容量,最小化平均成本.Cheng等[7-8]针对两设备一缓存系统,研究了当上游设备退化服从几何过程、非静态伽马过程时的固定周期维护策略.Gan等[9]考虑了维护、缓存和备件的相互影响.Niyamosoth等[10]研究了包含一台租赁设备和缓存区的系统,优化出租人的维护周期和承租人的缓存容量以最小化总成本.Nahas等[11-13]研究了维护频率与平均故障间隔时间的关系,通过遗传算法求解缓存和维护联合优化问题.Renna[14]对串行多设备生产线进行了类似的研究.Zandieh等[15]建立了包含生产率最大化、缓存区最小化及不合格品数最小化的多目标联合优化模型.
上述研究的优化目标多为固定的维护周期,虽然建模过程中考虑了缓存,但没有考虑特定缓存状态对维护决策的影响.因此部分学者通过建立马尔科夫模型优化设备维护策略,维护决策同时取决于设备退化状态和缓存状态.文献[16]只考虑上游设备的退化和维护,运用马尔科夫决策理论计算并证明了控制限策略是使得平均成本最优的策略.Dimitrakos等[17]扩展了文献[16]中的模型,考虑上游设备的非平稳退化和更完善的成本结构,将维护持续时间从几何分布拓展到连续分布.Karamatsoukis等[18]在上述研究的基础上考虑了上下游两设备的退化和维护决策.Fitouhi等[19]则考虑在生产率水平约束下最小化总成本.Zhou等[20]针对具有两个多组件系统和一个中间缓存区的串并联系统的预防性维护问题,开发了马尔科夫决策方法.Gan等[21]关注了缓存、预防性维护及部件更换之间的相互作用,除维护策略外优化备件一般订单的下达时间.
这类研究多假设故障维修和预防性维护是完美的,但这在实际中难以实现.此外,已有文献多以总成本作为优化目标,但缓存区的设置不仅引起成本变化,也会延长设备运行时间进而提高产量.针对这些问题,本文在现有文献的基础上有以下创新点:①考虑系统内其他设备和缓存状态的影响,针对特定系统状态进行预防性维护决策;②考虑不完美维护,维护改善设备状态但不一定使其恢复全新,基于此构建马尔科夫状态转移模型,更符合实际生产;③用系统运行利润代替成本作为优化目标,可以更全面地衡量维护决策的效果.
本文以两设备一缓存生产系统为研究对象,同时考虑上下游设备的退化和不完美维护,以两设备状态和缓存量描述系统状态,建立离散时间的马尔科夫决策模型.以系统的长期期望运行利润最大化为目标,优化不同系统状态下的设备维护决策.
1 问题描述
本文以两设备一缓存生产系统为研究对象,如图1所示,其中M1、M2分别为生产系统的上下游设备,B为缓存区.零件从系统外部流向M1,经由M1加工后流向缓存区,M2从缓存区提取零件,加工完成后流出系统.缓存容量为K,当缓存未满且两设备运行时,M1以生产率p供应缓存,M2以生产率d(p>d)消耗缓存.一旦缓存达到容量限制,将M1生产率从p调整为d.
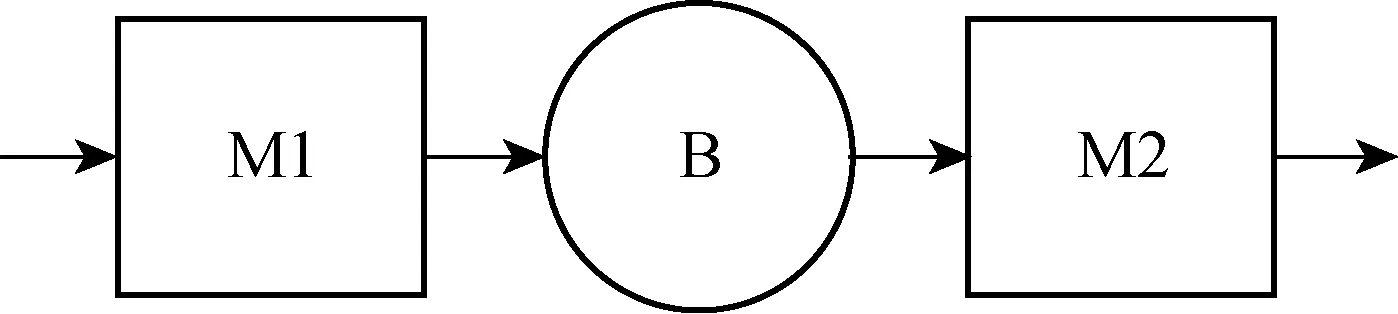
图1 两设备一缓存生产系统Fig.1 Two-machine one-buffer production system
上下游设备的失效率随役龄的增加而增加,可在离散等距的观测周期τ=0,1,…进行检查评估以确定设备状态.以上游设备为例,M1共有3m个状态:①根据失效率将运行状态划分为1,2,…,m,数值越大表示设备状态越差;②若设备在运行状态i发生故障,则转移至状态m+i,因此m+1,m+2,…,2m表示设备的故障状态,数值越大表示故障越严重,越不易维修,设备故障后立即小修,小修完成后返回故障前状态i;③若设备在运行状态i进行维护,则转移至状态2m+i,故2m+1,2m+2,…,3m表示维护状态,数值越大表示状态越差,越不易维护,不完美维护完成后,设备有可能转移至不劣于维护前状态i的任一运行状态j,即满足1≤j≤i.同样地,M2共有3n个状态.
生产系统的状态用3个变量(i,i′,κ)描述,i和i′分别表示上下游设备的状态,κ为缓存量.则生产系统的状态空间S={(i,i′,κ)|i∈{1,2,…,3m},i′∈{1,2,…,3n},κ∈{0,1,…,K}}.
两设备均有3种可以执行的行动,即a,a′∈{0,1,2},0表示不采取任何措施,1和2分别表示维护和小修,行动集用Π表示.设备处于运行状态时,需要决策是否进行预防性维护,可选择行动0或1;当且仅当设备故障时选择行动2.
本文采用离散时间的马尔科夫决策过程对带缓存双机生产系统进行预防性维护决策.以最大化的系统长期运行利润为目标,决策当上下游设备分别处于不同状态,以及不同的缓存状态下,是否进行设备的预防性维护.
为便于模型的构建,结合生产实际,本文提出如下假设:
(1) 初始时刻两设备均处于最佳状态,缓存量为0;
(2) 上下游设备的状态及状态转移相互独立;
(3) 上游设备不会出现零件供应短缺,下游设备不会阻塞;
(4) 小修和预防性维护持续时间均服从几何分布;
(5) 由于设备故障是非计划性的突发情况,因此小修过程相比于预知的维护更为复杂,故小修的期望完成时间和成本均大于预防性维护[22].
2 马尔科夫决策模型
2.1 设备状态转移模型
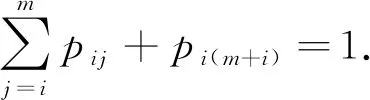
故障状态m+i不能从i以外的其他运行状态到达,即对于1≤i,j≤m且i≠j,满足pj(m+i)=0.μi为状态m+i的小修成功率,当M1处于故障状态m+i,下一周期只会:① 小修完成,以概率μi转移至故障前运行状态i;② 小修未完成,状态不变,即p(m+i)(m+i)=1-μi.M1运行状态和故障状态下的状态转移如图2所示.
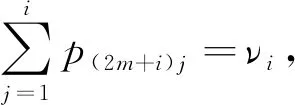
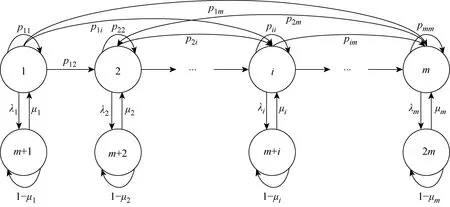
图2 M1运行和故障状态转移Fig.2 Transition of working and failure states of M1
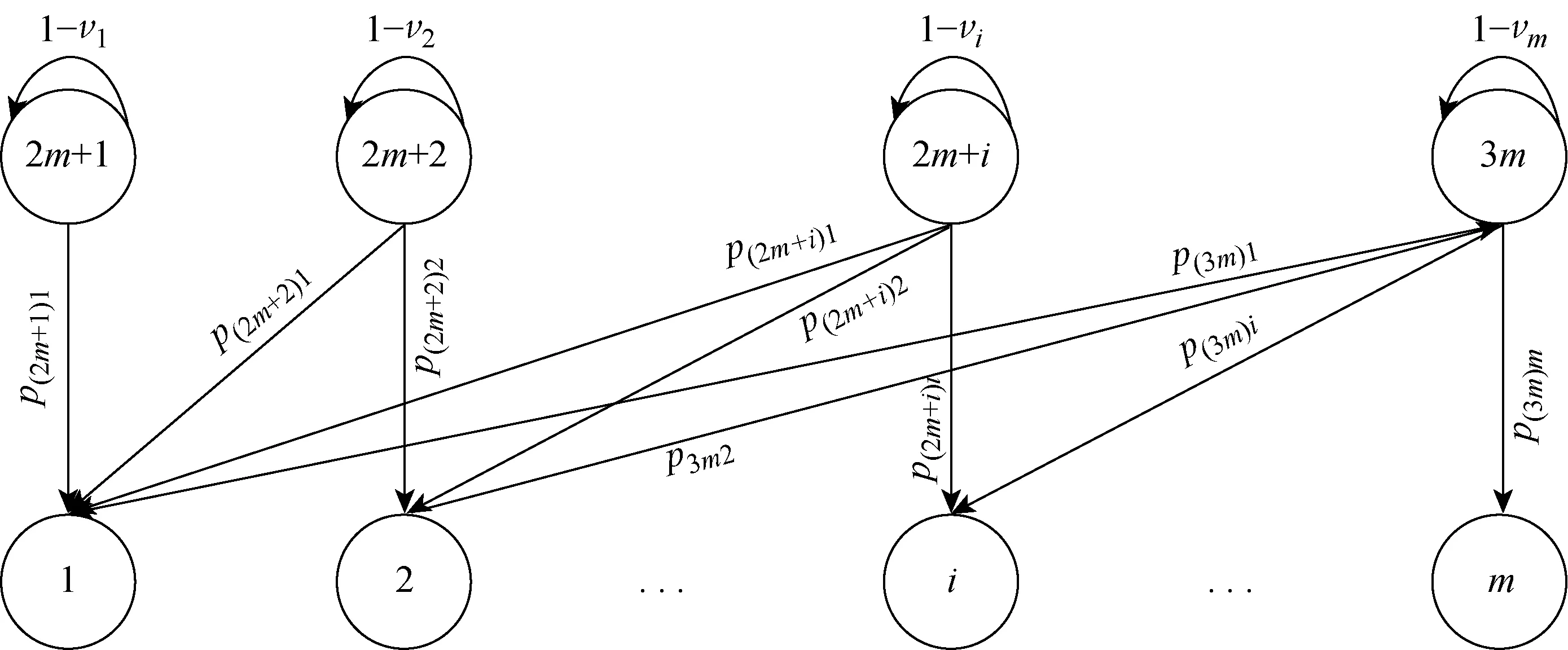
图3 M1维护状态转移Fig.3 Transition of maintenance states of M1
小修和维护的成功率与维护前的运行状态i有关,对于1≤i
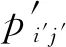
2.2 系统状态转移概率
对于带缓存双机系统的状态转移概率,若系统在周期τ处于状态s,当采取策略π=(a,a′)时,下一周期系统状态转移至状态u的概率Psu(π)为
(1)
(2)
(3)
(4)
(5)
(6)
(7)
上述公式均满足1≤i≤j≤m,1≤i′≤j′≤n,0≤κ≤K.式(1)、(2)表示两设备均运行时的转移概率;式(3)表示M1在状态i进行维护且本周期内维护未完成的概率;式(4)表示两设备均停机维护且均在本周期完成的概率;式(5)表示M1运行,M2故障小修且修复完成的概率;式(6)表示M1小修,M2维护且均完成的概率;式(7)为两设备同时小修且本周期内未修复成功的概率.其他状态下的转移概率与上述概率结构相似,不再赘述.
上述状态转移概率公式体现了状态空间的选择.以式(1)、(2)为例,当本周期初的系统状态为(i,i′,κ)且采取的策略为两设备均不维护时,本周期内两设备同时运行.当本周期结束时,缓存量只可能增加为κ+p-d或因容量限制保持K不变,且两设备只可能以相应概率转移至运行状态j和j′或出现故障停机.即下一周期生产系统只会在状态空间中选择其可能到达的状态,到这些状态的转移概率大于0,而到其他状态的转移概率为0.
2.3 利润函数
若周期τ系统处于状态s并采取策略π=(a,a′),在该周期内取得的利润用R(s,π)表示.R(s,π)为该周期内的收入与成本之差,本文考虑的成本结构包括材料成本、设备运行成本、缓存成本以及维护小修成本.
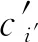
R((i,i′,κ),(0,0))=dg-min{p,K+d-κ}(cr+
(8)
(9)
R((i,n+i′,κ),(0,2))=-min{p,K-κ}(cr+
(10)
(11)
(12)
R((2m+i,n+i′,κ),(1,2))=
(13)
上式均满足1≤i≤m,1≤i′≤n,0≤κ≤K.式(8)表示两设备均运行时,该周期内的系统利润;式(9)表示当M1维护,M2运行时,周期内的系统利润;式(10)表示当M1运行,M2小修时,周期内的系统利润;式(11)~(13)表示上下游设备同时停机,进行维护或小修时,周期内的利润.其他状态下的系统利润与上述利润结构相似.
2.4 长期期望利润模型
考虑无限阶段的马尔科夫决策过程,对生产系统的长期期望利润进行建模.为保证长期期望利润收敛,取折扣因子0<α<1.则经过τ个周期的期望利润Vτ(s)满足
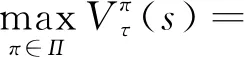
(14)
s∈S,τ>0
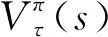
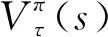
(15)
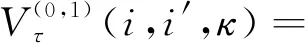

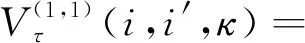
当一台设备发生故障小修而另一台设备正常运行时,以M1故障为例,采取不同维护策略时的期望利润为

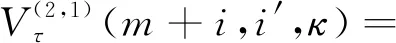
当一台设备正在进行预防性维护而另一台设备正常运行时,以M2维护为例,采取不同维护策略时的期望利润为
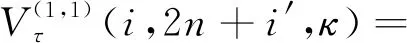
当上下游设备均发生故障小修时,期望利润为
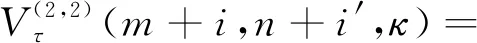
R((m+i,n+i′,κ),(2,2))+
根据假设(1),初始状态为s=(1,1,0),则当τ趋于无限大时,系统长期期望利润V*满足
(16)
式(16)即为维护决策的目标函数,通过最大化长期期望利润,即可得到各个系统状态下两设备的维护决策.
3 数值分析
值迭代方法是应用最为广泛的求解无限阶段折扣马尔科夫决策过程的方法,本文通过值迭代方法求解最优维护策略的步骤如下:
步骤1:初始化,对任意系统状态s=(i,i′,κ)∈S,设置V0(s)=0,令τ=1,取ε为一个足够小的正数;
步骤2:对于每个状态s∈S,通过计算式(14),求得Vτ(s);
步骤3:若|Vτ(s)-Vτ -1(s)|<ε,进入步骤4,否则,令τ=τ+1,返回步骤2;
步骤4:输出各状态下最优的设备维护决策,输出初始状态为(1,1,0)的最优长期期望利润V*,算法结束.
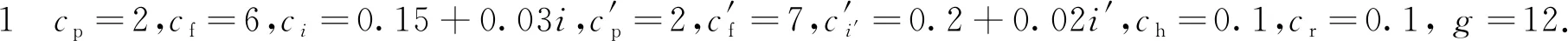
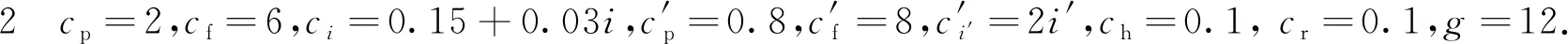
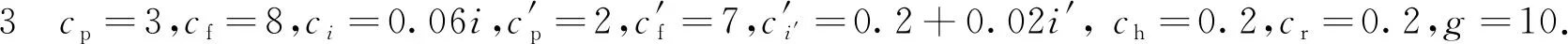
代入上述参数对模型进行求解,3个算例得到的最大长期期望利润分别为94.83、65.78及62.44,对应各系统状态下M1最优的预防性维护决策如表1所示,括号里的3个数字从左往右依次为3个算例的求解结果,表示在给定的M2状态i′和缓存状态κ下,M1的最优预防性维护起始状态i(i′,κ)*,即M1状态优于该值则正常运行,否则进行维护.
M2的最优预防性维护起始状态i′(i,κ)*如表2所示.

表1 M1最优维护策略Tab.1 Optimal maintenance policy of M1
从上述3个算例的求解结果都可以看出,对于一台设备而言,当缓存量和系统内其他设备处于不同状态时,其执行预防性维护的起始状态是不同的,即缓存量和其他设备所处的状态都会对其维护决策造成影响.接下来针对算例1进行更为详细的数据分析.
分别取上下游设备处于状态1及其对应的小修状态7和维护状态13,绘制另一台设备的维护起始状态与缓存状态的关系图,如图4、5所示.图中3条不重合的曲线体现了系统内其他设备状态对维护决策的影响,曲线的变化趋势体现了缓存对维护决策的影响.可以看出,两设备都倾向于在另一台设备停机时提前进行维护.M1受缓存状态的影响更大,更倾向于在缓存量能够满足M2需求时提前维护.M2则为保证产出,在M1运行或缓存充足时都不会提前维护,只有M1停机且缓存量不足时,才会进行提前维护.
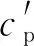
图4 不同系统状态下的M1维护起始状态Fig.4 Initial maintenance states of M1 in different system states

表2 M2最优维护策略Tab.2 Optimal maintenance policy of M2
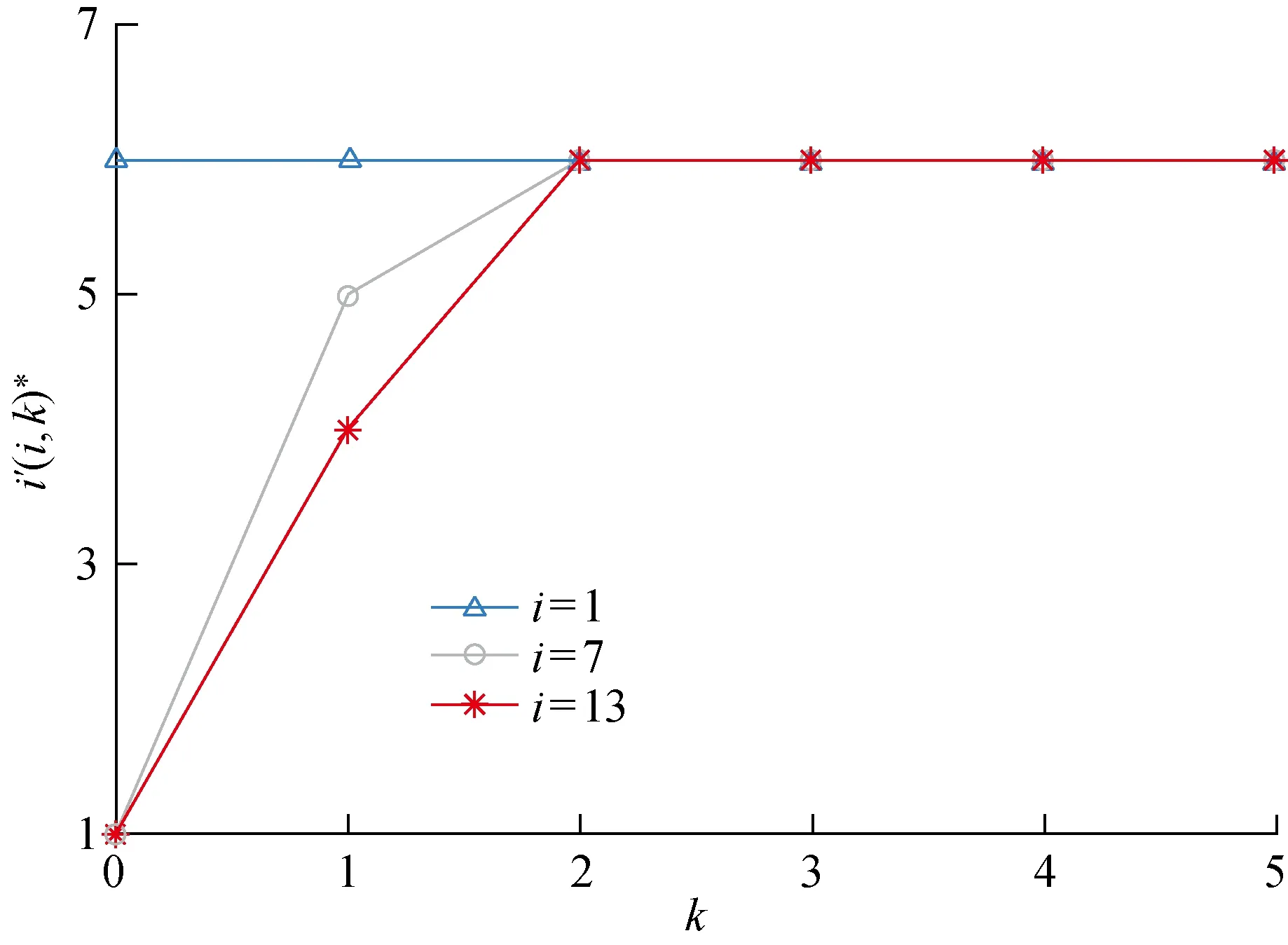
图5 不同系统状态下的M2维护起始状态Fig.5 Initial maintenance state of M2 in different system state

图6 不同cp和下的系统利润Fig.6 System profit at different cp and values
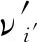
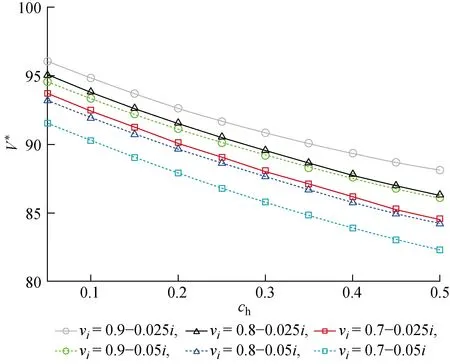
图7 不同ch和νi下的系统利润Fig.7 System profit at different ch and νi values
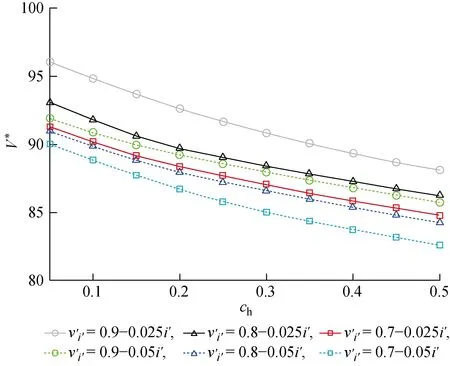
图8 不同ch和下的系统利润Fig.8 System profit at different ch and values
4 结语
本文建立了两设备一缓存的生产系统模型,上下游设备均有可能故障停机,故障后立即小修,正常运行时可以选择是否进行预防性维护,小修和维护都是不完美的.通过建立马尔科夫决策模型,考虑材料成本、设备运行成本、缓存成本以及维护小修成本,建立了系统的长期期望利润模型作为优化目标,在不同系统状态下进行设备的维护决策.算例求解结果表明,系统状态会影响设备的维护决策,根据系统状态采取更灵活的维护策略是有必要的.
本文结果对包含两台以上设备生产系统的设备维护问题具有一定的参考作用,未来可对更为复杂的生产系统进行进一步研究.

