三叶片H型垂直轴风力机风振与减振研究
杨梦姚,毛璐璐,韩兆龙,b,c,周 岱,b,c,雷 航,曹 宇
(上海交通大学 a. 船舶海洋与建筑工程学院;b. 海洋工程国家重点实验室;c. 水动力学教育部重点实验室, 上海 200240)
风能是一种重要的能源.2018年底,我国风电累计装机容量2.1亿千瓦,占全球风电市场的三分之一以上[1].风力发电机根据转动轴与来风方向的相对位置分为水平轴风力机和垂直轴风力机两类.以H型风机为代表的垂直轴风力机具有产生噪声更小、整体结构更简单、生命周期更长、发电效率更高等特点,具有广阔的发展前景[2].H型垂直轴风力机通常由2~6片与转轴平行的叶片组成,其结构特征使得必有叶片会处于迎风位置,易产生离心力,主轴螺栓连接处易断裂,叶片在风荷载的作用下易产生振动问题,抗风能力较弱[3].

图1 垂直轴风力机风振与减振技术路线图Fig.1 Flowchart of wind vibration and vibration reduction of VAWT
近年来,研究者对垂直轴风机(VAWT)风振响应开展了一些研究[4-7].潘博等[8]提出研究垂直轴风机必须考虑风致振动及气动力与叶片的共振.Campos等[9]提出结构柔度问题在风机生命周期评定中十分重要.对结构耗能减振,设置阻尼器是较为常用的方法.刘保文等[10]对大跨度斜拉桥桥塔设置纵向阻尼器,有效减小了主塔在地震荷载作用下的内力,使得内力重新分布,改善了结构受力性能.周云等[11]在某高层建筑上布置若干黏滞阻尼器,减震效果良好.目前,关于垂直轴风力机减振的研究较少.本文针对H型垂直轴风力机振动问题,在风机结构的不同位置上分别布置阻尼器,采用数值模拟的方法分析其耗能减振能力.
基于计算流体动力学,采用STAR-CCM+软件建立垂直轴风力机的空气动力学模型,计算风机旋转时叶片所受气动荷载.将气动荷载在MATLAB软件中进行拟合,获得时序性风机叶片荷载函数,并将其施加到基于ANSYS软件建立的垂直轴风力机的结构模型上,从而进行动力学分析,得到风机结构的位移响应时程.为抑制风力机的振动,在风机不同位置处施加基于COMBIN40单元而模拟的阻尼器,计算阻尼器耗能减振的能力.
1 风力机力学模型
本文的技术路线如图1所示.H型垂直轴风力机的几何模型如图2所示(其中数字为节点编号),其通常由2~6片叶片组成.目前2叶片或3叶片风机在风电市场上应用较广[1],兹选取典型3叶片H型垂直轴风力发电机为对象,研究风机旋转时风荷载对风机振动稳定性的影响.垂直轴风机多采用对称翼型,故本文中风机的叶片翼型截面选择NACA-0021[12],D型主梁处材料采用碳纤维,叶片蒙皮处材料采用玻璃纤维.主轴与支杆材料采用Q345钢材[13],弹性模量E=200 GPa,泊松比μ=0.17,密度ρ=7.8×103kg/m3.为减小计算量,选用某大型10 MW风机的100∶1缩尺模型.风机模型的几何尺寸为:弦长C=0.265 m,支撑杆长D=0.8 m,叶片高度H=1.2 m,主轴和撑杆截面皆取圆截面,主轴直径为0.2 m,撑杆直径为0.1 m.
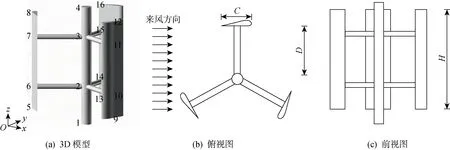
图2 H型垂直轴风力发电机的几何模型Fig.2 Geometric model of a H-rotor type vertical axis wind turbine
2 分析方法
2.1 风力机风荷载模拟
由于风机翼型截面的复杂性,故较难手动计算出风机表面荷载的数值.计算流体动力学方法常应用于解决流固耦合问题[14],兹基于计算流体动力学理论开展H型垂直轴风力机叶片表面风荷载时程的数值模拟研究.采用雷诺平均(Reynolds Averaged Navier-Stokes, RANS)和标准k-ε湍流模型[15]作为数值模拟方法,运用STAR-CCM+软件进行数值计算.雷诺平均纳维-斯托克斯(N-S)方程为
(1)
式中:ui、uj分别为i、j方向的速度分量,i、j为坐标轴方向;t为时间;xi、xj为坐标;ρ为流体密度;p为压力;ν为动力黏度系数;上标“ ′ ”代表来流的脉动值.
由于本文的研究目的侧重于风机减振,所以对于风机的气动荷载采用一些简化计算,具体如下:① 风力机处于自然大气边界层中,因其叶片高度不大,故可不考虑风速梯度的影响.② 考虑到在实际工程中,近地面的湍流强度较大.且当风力机转速恒定时,来流风速越低,风机叶尖速越大,因风轮转动引起的湍流强度随之增大.在这种高叶尖速比的条件下,湍流强度的大小会对风力机的气动力造成一定影响[16].为简化模型,本文的计算条件参考相关风洞实验条件设置[16],其中来流风速为8 m/s,湍流度为0.005.③ 因本文的研究对象是风力机的缩尺模型(1∶100),故本文的雷诺数是原模型的1/100,根据文献[16],雷诺数越大,风机的空气动力学性能越好,同时,由于叶片升力系数的增大,转子转矩也更大.因此本文所采用的缩尺模型的气动载荷特性与原模型存在一定的偏差,模型的折算气动载荷略小于实际载荷.④ 在CFD数值模拟过程中,为简化计算,未考虑叶片结构变形的影响.
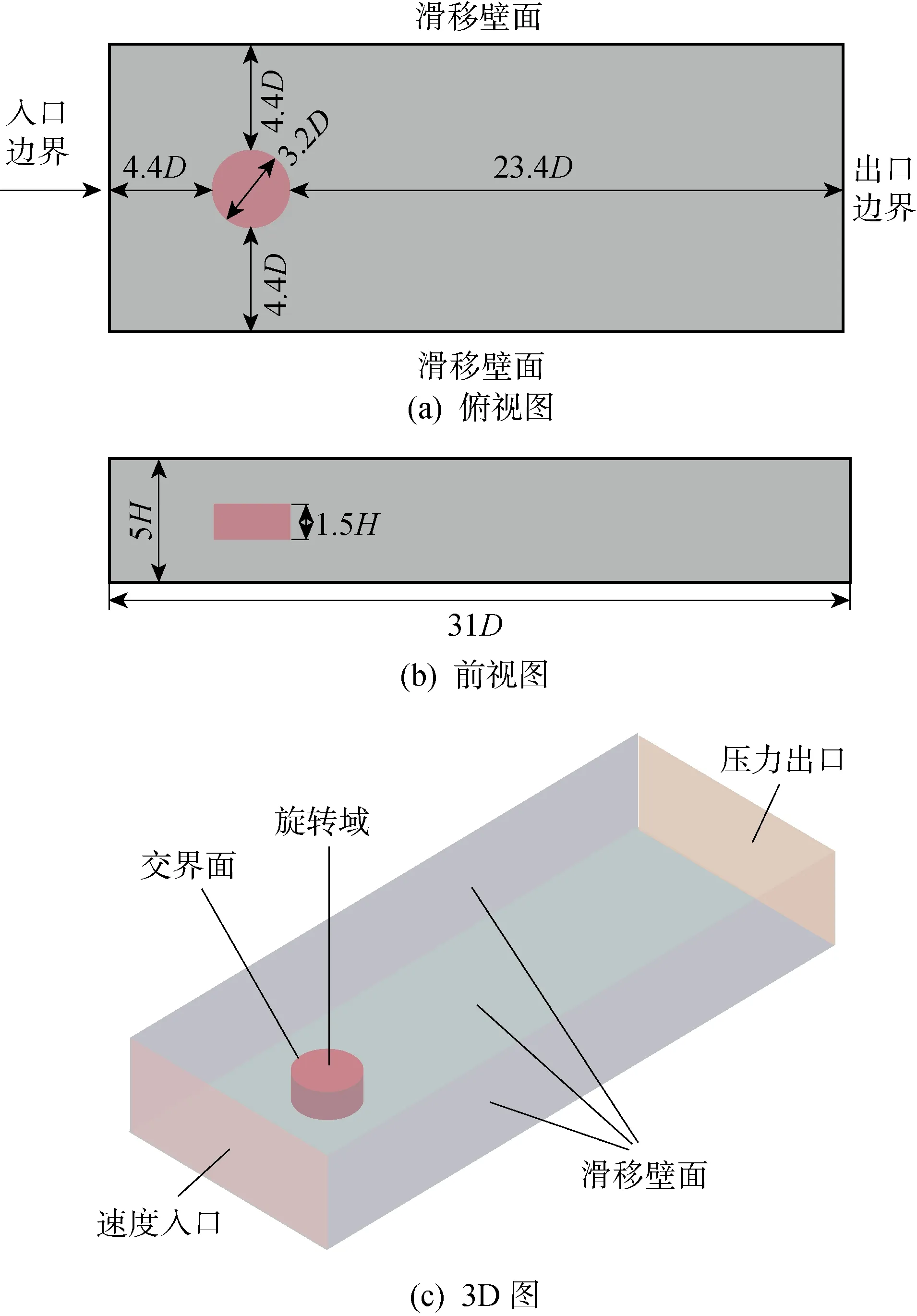
图3 风场计算域与边界条件Fig.3 Calculation domain and boundary conditions of wind field
为减少边界条件的影响,在选取风场计算域时,取其尺寸为31D×12D×5H[17]即24.8 m×9.6 m×6 m.将垂直轴风机的中心置于计算域的前1/3处,以确保计算域风场流动发展完全,如图3所示.入口选用速度边界条件,计算风速取8 m/s;出口选用自由扩展边界条件;风轮区域流体定义为旋转流体,风轮定义为相对旋转固体壁面;壁面选用滑移壁面.对风场计算域进行网格划分,使近叶片周围的网格较密集,远离叶片的网格较稀疏.由此共划得棱柱形网格约1.89×106个,风场计算域的阻塞率小于3%,无量纲化的壁面距离y+<1,满足数值模拟对于网格的要求[18].
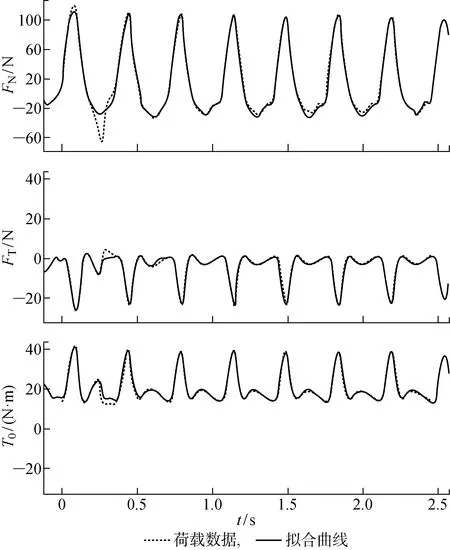
图4 叶片气动荷载时程曲线与函数拟合结果对比Fig.4 Comparison of blade aerodynamic load time history curve and function fitting results
本文计算得到叶片的转矩荷载时程曲线结果如图4所示.图中:T0为转矩,FT为切向力,FN为法向力.将其与Lei等[19]的转矩时程曲线进行对比,发现具有相同的波形且荷载数值接近.
由于风机的气动荷载呈现周期性,所以可采用周期函数对其进行拟合.在MATLAB中,采用多阶正弦函数对风机的切向力、法向力及转矩时程曲线进行拟合,获得相应的荷载函数,便于在ANSYS中对结构进行瞬态分析.以叶片的法向力为例,任一时间序列的荷载函数可近似模拟为
(2)
式中:fn(t)为t时间下的叶片法向力;ai、bi及ci分别为第i个正弦函数的各项系数.
如图4所示,法向力、切向力及转矩的荷载函数曲线的拟合效果较好,几乎与气动荷载时程曲线保持一致.因此,采用多阶正弦函数对气动荷载数据进行拟合的方法是可行的.
2.2 结构风致振动响应分析
运用ANSYS/Mechanical APDL 18.2软件开展有限元数值模拟研究,采用Newmark-β方法进行瞬态分析.Newmark-β方法是一种隐式时间积分方案,具有二阶时间精度[20],此处选取γ=0.5,β=0.25(γ和β分别为控制数值分析精度和稳定性的参数),即平均常加速度法.边界约束条件为底端固接,在叶片表面施加气动荷载,用四面体型三维实体单元对模型进行网格划分,共得到5.234×104个网格单元.图5为叶片表面所施加的荷载示意图.

图5 叶片施加荷载示意图Fig.5 Schematic diagram of blade loading
风机结构在荷载激励下的运动方程可以表示为
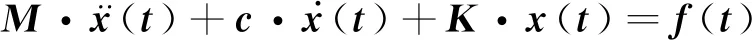
(3)
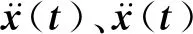
用有限元方法求解上述方程,可以得到各节点的风致响应.
2.3 阻尼器模拟
在建筑物或空间结构上安装单个或多个阻尼器,可以抑制结构的振动响应[21-22].阻尼器会随着风机的振动而振动,其产生的惯性力作用可部分抵消风荷载对风机所产生的力作用,从而减小振动水平.为验证阻尼器在垂直轴风力机上的减振性能,在原结构(模型1)的主轴与支杆连接处,即节点2和节点3处分别增加1个阻尼器,得到模型2和模型3,如图6(a)、(b)所示.

图6 加阻尼器后风力机模型示意图与弹簧-阻尼单元Fig.6 VAWT model with dampers and spring-damping unit
本文参考文献[23],采用多维减振阻尼器,它是6个自由度的并联机构,由法兰盘、连接耳板及阻尼元件3部分组成.其阻尼原件主要是由6个黏弹性阻尼单元构成的,在ANSYS软件中,将其简化为3个一维轴向COMBIN40 单元,提供三向平动自由度.3个一维转动COMBIN40单元提供三向转动自由度[23].COMBIN40单元是由相互平行的弹簧滑动器和阻尼器组成,并且串联着一个间隙控制器的弹簧单元.在本文的计算中,将其简化为相互平行的弹簧和阻尼器单元,如图6(c)所示,其中k为弹簧刚度,c为阻尼系数.
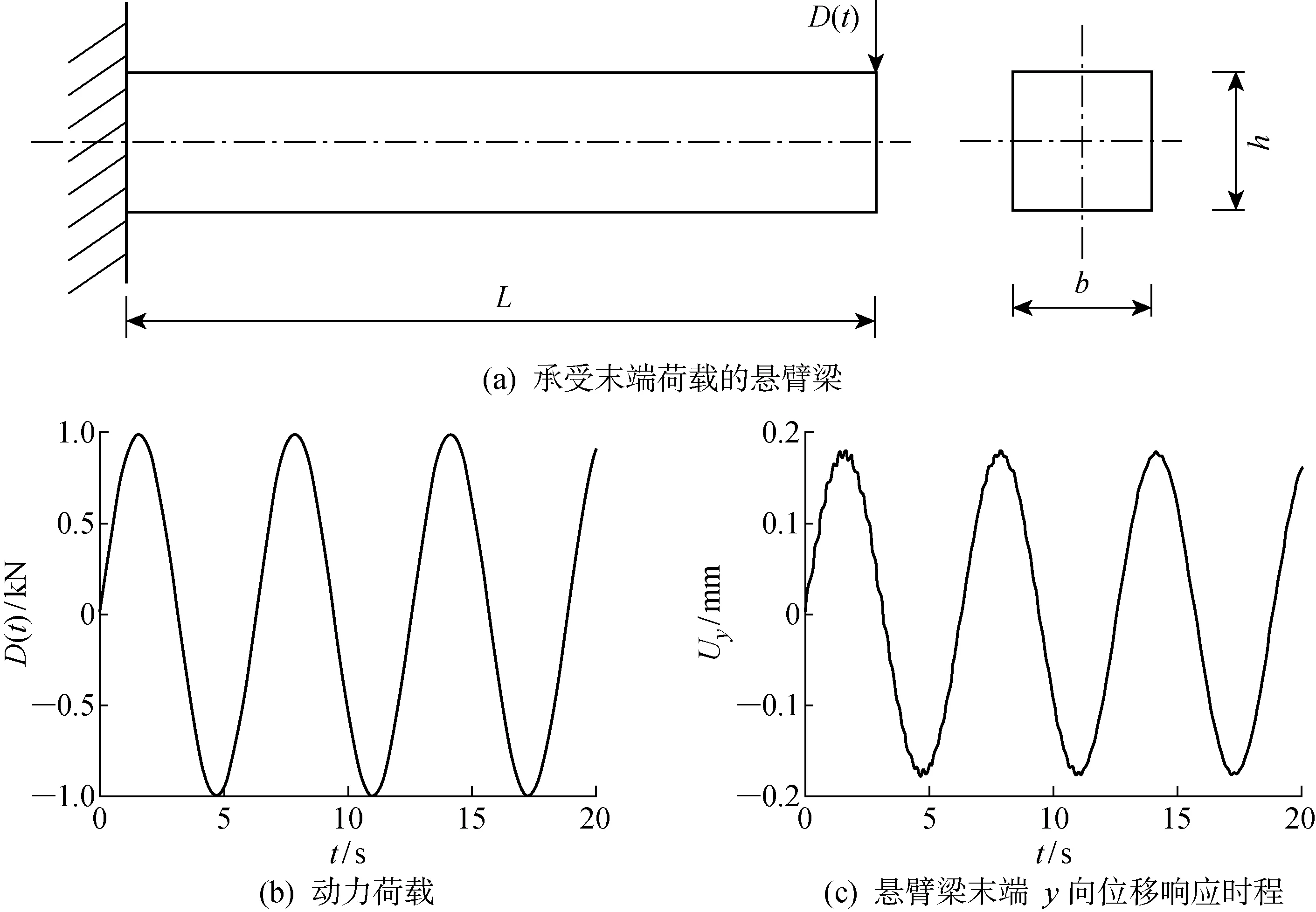
图7 悬臂梁受动力荷载的时程响应Fig.7 Time-history response of cantilever beam at dynamic load
阻尼元件的刚度和阻尼系数对于减振效果的影响非常明显.具体体现为:当阻尼元件刚度不变时,峰值位移在整体范围内随着阻尼系数的增大而减小,当刚度足够大时,阻尼系数的改变对峰值位移的影响不大.当阻尼系数不变时,峰值位移在整体范围内随着刚度的增大而减小,当阻尼系数足够大时,刚度的改变对峰值位移的影响不大.基于上述规律并经过反复试算,最终假定阻尼元件刚度为5×107N/m,阻尼系数为2.5×107N/(m·s).
3 数值算例验证
3.1 动力作用下悬臂梁变形验证
在结构力学中,二维悬臂梁问题既是经典问题也是基准问题,被广泛用于验证或测试研究者提出的各种数值方法.为验证本文方法的可靠性,考虑了在简谐荷载作用下的悬臂梁变形问题.问题定义及荷载曲线如图7(a)、(b)所示.悬臂梁的长度L=10 m,梁截面宽度b=1 m,高度h=1 m,弹性模量E=2.3×1010Pa,泊松比μ=0.27.在悬臂梁自由端施加简谐荷载D(t),荷载函数为D(t)=1 000sint,如图7(b)所示.计算所得最大位移为0.177 mm,如图7(c)所示,图中Uy为悬臂梁末端y向位移时程,与文献结果[24]对比,响应幅值与响应频率与文献结果相符.
3.2 时间步长选取
对于运用ANSYS分析瞬态动力学问题,选取不同的时间步长和时间步会对结果产生影响.时间步长越小,计算精度越高,但相应会造成计算资源的浪费,因此在数值模拟前应当先选取合适的时间步长.兹对计算模型进行在3种时间步长下的模拟,即:0.004、0.002及0.001 s,分别得到对应的结构关于x轴的底部弯矩M0(见表1):
(4)
式中:hi为结构物的高度;P(x)为x高度处结构表面压力;A,Ai为受力面积.

表1 不同时间步长下底部弯矩比较
从表1看出,当时间步长为0.002 s时,Mx为107.47 N·m,与时间步长取0.001 s时所得的结果相差仅0.7%,可看作近似相等.故时间步长为0.002 s时,既能保证所得结果的精确性,也能节省计算资源.兹选取时间步长为0.002 s.
4 数值结果与分析
4.1 风荷载模拟
本文仅考虑来流风速8 m/s,风机转子转速17.92 rad/s[19]的工况下,垂直轴风机所承受的气动荷载.风机旋转1个周期所需的时间 0.350 6 s.图8所示为第6个周期计算结束即t=2.103 6 s时其中1个叶片的压力(p′)分布,图中坐标系为叶片的局部坐标系.结果表明:较大的正压力出现在叶片翼型前缘,与文献结果相符[25].图4所示为叶片上的瞬时风压随时间的变化趋势.可见,在前两个周期内,相邻周期的压力峰值差距较大,在风机旋转了2~3个周期之后,压力数值趋于稳定.

图8 风机叶片压力云图Fig.8 Pressure cloud diagram of fan blade
4.2 风机结构的风致响应分析
在运用ANSYS软件计算垂直轴风力机的振动响应时,由于垂直轴风力机旋转过程中叶片的气动荷载随时间呈周期性变化,所以,将周期性变化的气动荷载加载到风机结构上,即是把原来的风载恒定,风机转动的问题转化成了风机不动,而风载随时间变化,从而计算风机的振动响应.在风机结构响应分析中,为简化计算,未考虑结构整体转动的自由度.同时,本文中未考虑风机转动对风振响应的影响,风机转动可能会使风机的风振响应更为复杂,在后续研究中将进一步展开分析.
分析发现t=10 s时,结构的振动幅值较大,故选取t=10 s时刻下的总位移云图分析,如图9所示,
图中Usum为风力机结构的总位移.图9(a)所示为t=10 s时,原结构(模型1)的总位移云图.可见,模型1的最大位移发生在位于叶片顶端的节点16处,达到2.7 mm.即在该时刻下,风机的危险点为节点16,由于风机叶片的对称性,可重点关注叶片顶端节点.图9(b)所示为t=10 s时,在上部支撑杆处加了阻尼器后的模型2总位移图,此时最大位移发生在位于叶片底端的节点9处,数值为1.5 mm,下降达44.4%.图9(c)所示为t=10 s时,在下部支撑杆处加了阻尼器后模型3的总位移图,此时最大位移仍旧发生在位于叶片顶端,数值为1.6 mm,下降达40.7%.
为更清晰地对比结构的三向位移,用图10表示t=10 s时3个模型在x、y及z向的位移云图,其中,Ux、Uy及Uz分别对应模型在x、y及z向的位移.由图10对比x向位移数值,可见模型1的Ux分布在-2.7~1.0 mm,模型2的Ux分布在-0.5~0.8 mm,模型3的Ux分布在-0.9~0.9 mm,位移最大值全部发生在叶片顶端或底端.对比y向位移数值,可见模型1的Uy分布在-1.5~2.0 mm,模型2的Uy分布在-0.4~1.2 mm,模型3的Uy分布在-0.5~1.4 mm.对比z向位移数值,可见模型1的Uz分布在-0.13~0.25 mm,模型2的Uz分布在-0.04~0.04 mm,模型3的Uz分布在-0.05~0.05 mm.3个结构的x向和y向的位移数值较大且处于同一数量级,z向位移较小.
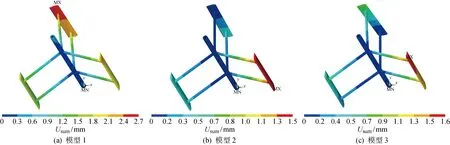
图9 不同垂直轴风力机模型总位移云图对比Fig.9 Comparison of total displacement contour map of different VAWT models
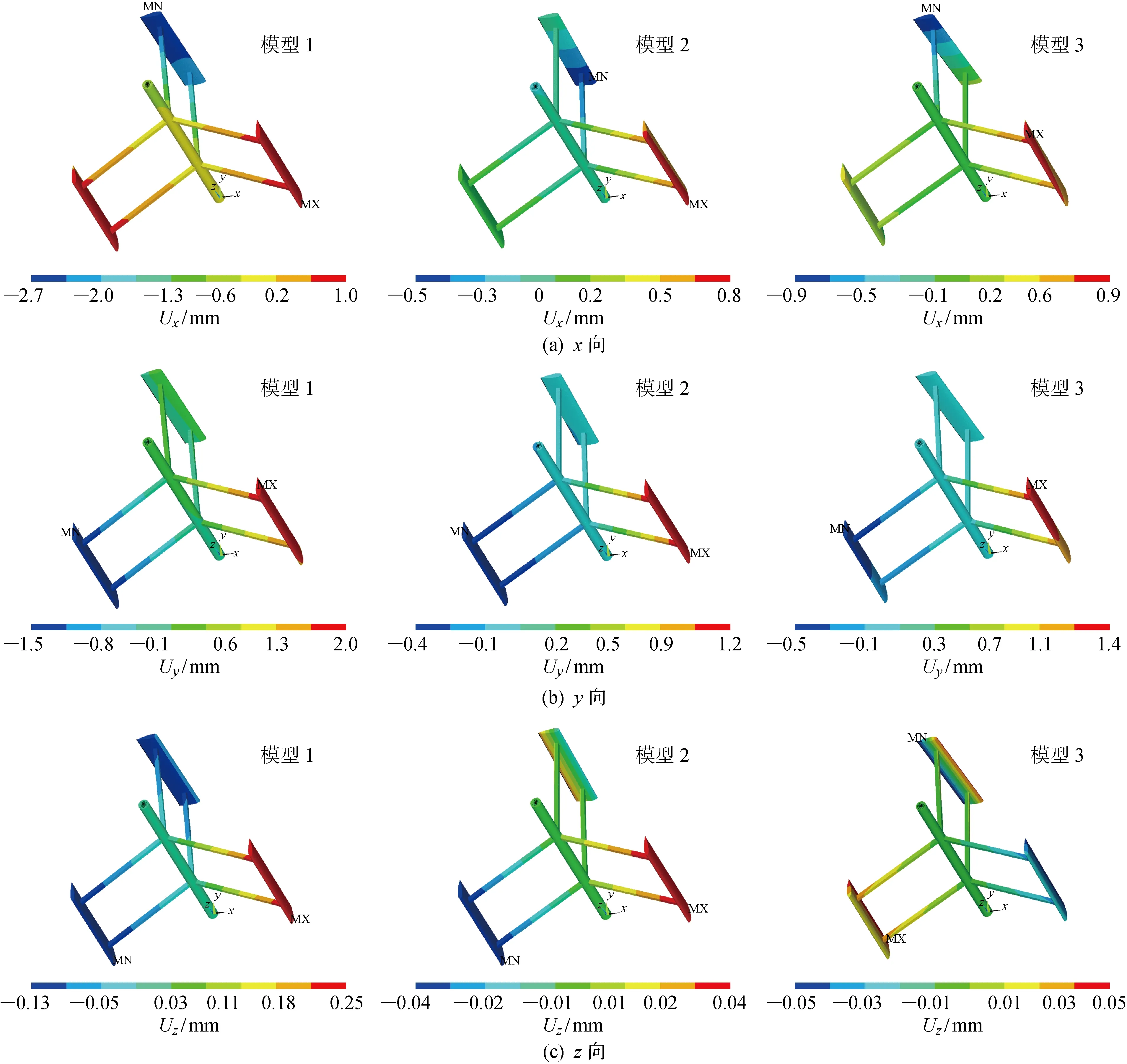
图10 风力机结构三向位移云图对比Fig.10 Comparison of three-way displacement contour maps of VAWT
由以上分析可知,原模型危险点出现在叶片顶端,故取节点8为对象,研究3个模型在风机叶片顶端的风致响应.又因x、y向位移数值较大,z向位移较小,故仅对比节点8的x、y向位移响应.图11所示为3个模型节点8的风致响应对比.图中Ux,8表示风力机节点8在x方向的位移,Uy,8表示风力机节点8在y方向的位移.可见,模型2和模型3在叶片顶端节点的位移抑制效果较为显著.表2所示为3个模型的节点8的三向位移改善率统计数据.可见,模型2在x方向的平均位移改善率约为44%,在y方向的平均位移改善率约为54%,在z方向的平均位移改善率约为5%.模型3在x方向的平均位移改善率约为40%,y方向的平均位移改善率约为53%,但在z方向未见明显改善.
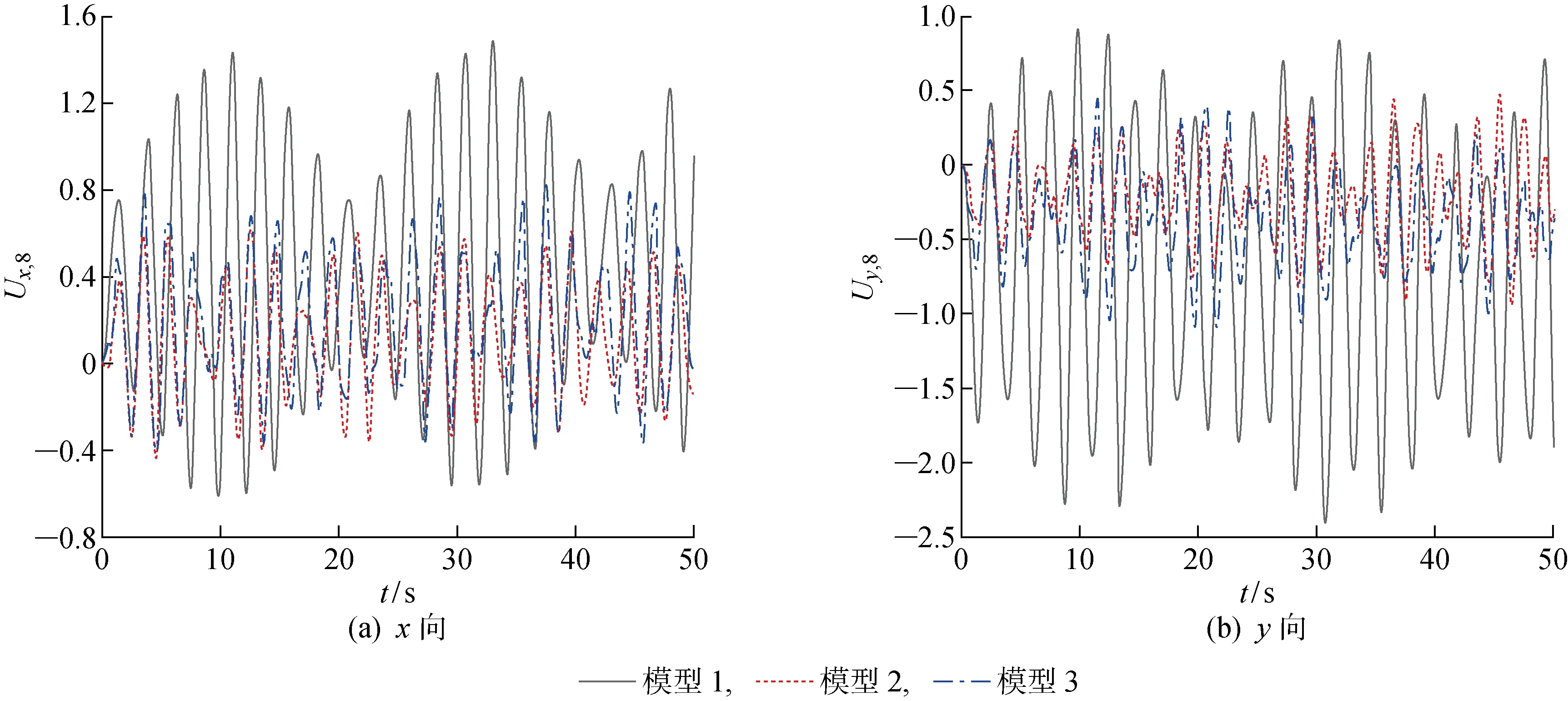
图11 3个模型节点8的风致响应对比Fig.11 Comparison of wind-induced response of three models at node 8

表2 3个模型节点8的三向风致响应统计
5 结论
本文针对H型垂直轴风力机振动问题,基于计算流体动力学方法,运用STAR-CCM+软件数值模拟风机旋转时叶片所受气动荷载,将气动荷载在MATLAB软件中实施函数拟合,获得时序性风机叶片荷载函数,再基于ANSYS软件开展时程分析,得到风机结构的三向位移响应时程.在风机不同位置处施加基于COMBIN40单元而模拟的阻尼器,数值模拟计算其耗能减振能力.主要结论如下:
(1) H型垂直轴风力机的风致位移响应曲线具有一定的周期性.t=10 s时,风机最大位移出现在叶片的顶端,风致x、y向位移处于同一数量级,z向位移较小.
(2) 在H型垂直轴风力机的主轴与支杆连接处布置阻尼器可降低结构位移响应,总位移最大降幅达44%.
(3) 阻尼器布置的位置与结构的位移改变密切相关.t=10 s时,在近风机叶片顶端连杆处布置阻尼器,结构最大位移出现在风机叶片底端,位移下降达44%;在近风机叶片底端连杆处布置阻尼器,最大位移则依旧出现在了风机叶片顶端,位移下降达40.7%.
本文成果可为垂直轴风力机减振研究提供一定的技术参考.

