不同温度下的乙烯-三氟氯乙烯共聚物薄膜单轴拉伸试验

刘昶江，赵 兵，陈务军

(上海交通大学 空间结构研究中心，上海 200240)

乙烯-三氟氯乙烯共聚物(ECTFE)是由三氟氯乙烯(CF2-CF-Cl)与乙烯(CH2=CH2)发生1∶1聚合反应得到的半晶高聚物，因具有良好的热、电、化学等性能，被广泛应用于化工、半导体、航空航天等领域[1].将ECTFE基材通过挤压、加工等工艺可以得到ECTFE薄膜，与典型的高分子热塑性薄膜相似，具有高透光度、耐化学渗透性、耐磨性、耐久性、各向同性及无经纬向纱线等特征，在建筑结构的大跨空间结构领域具有广阔的应用前景[2-3].

在众多含氟共聚物材料中，乙烯-四氟乙烯共聚物(ETFE)薄膜具有与ECTFE薄膜相近的物理、化学、热、电和力学等性质，自1995年起作为建筑与结构材料而被广泛应用于体育场、体育馆、温室和展览馆等大跨空间结构的屋面与立面[3-5].因此，针对ETFE薄膜已经展开的相关研究，对ECTFE薄膜与结构研究工作的开展具有良好的参考意义.Moritz[6]率先展开了对ETFE薄膜材料力学性能的试验研究.Galliot等[7-8]研究了ETFE薄膜的单轴拉伸力学性能.Hu等[9]研究了ETFE薄膜的循环拉伸与高温徐变等力学性能.Zhao等[10]对应用于双层气枕结构的ETFE薄膜在实际工作中的力学性能进行了试验与研究.吴明儿等[11]对ETFE薄膜材料进行了单轴拉伸试、循环与徐变等试验研究.赵兵等[12]研究了基于平面裁切成形ETFE双层气枕的结构行为.

ECTFE薄膜应用于建筑工程领域，其力学性能是主要的考察因素.然而，目前鲜有针对ECTFE薄膜力学性能的研究，相关公开文献较少.王文贵等[1]围绕ECTFE材料及实验室制备薄膜的基本特性进行了研究，陈务军等[2]对不同拉伸速率下的ECTFE薄膜单轴拉伸力学性能进行了试验与分析.由ETFE薄膜结构的工程应用可知，该类材料在实际使用过程中需要经受高-低温环境变化[13]，故亟需对ECTFE薄膜力学性能的温度依赖特性开展研究工作.

本文对不同温度下的ECTFE薄膜单轴拉伸力学性能进行系统试验研究，为ECTFE工程应用提供支撑，并为ECTFE应力应变行为的本构模型建立奠定试验基础.

1 不同温度下的ECTFE薄膜单轴拉伸试验

1.1 试验材料与试件尺寸

试验选取厚度为250 μm的ECTFE薄膜，由于ECTFE材料为各向同性材料[2]，因此在MD方向裁取试样.根据标准《塑料薄膜拉伸性能试验方法：GB/T 1040.1-2006》[14]进行试样设计和制备，使用锋利的裁刀将材料制成哑铃形试样，如图1所示，其中R为夹持端的倒圆角半径.

ECTFE薄膜和ETFE薄膜[3]的主要性能对比见表1.可以看出，ECTFE薄膜的灰度仅1.2%，透光性能胜过ETFE薄膜.ECTFE薄膜与ETFE薄膜的基本力学性能相似，因此作为结构材料的建筑应用前景广阔.

图1 试样尺寸和裁刀 (mm)Fig.1 Dimensions of specimen and cutting model (mm)

表1 ECTFE薄膜和ETFE薄膜的主要性能对比

图2 ECTFE薄膜在不同温度下的应力-应变曲线Fig.2 Tensile curves of ECTFE foil at various temperatures

1.2 试验分组与条件

1.3 试验方法与设备

试验在温控箱中进行，每组试验在温度达到要求并持续10 min后进行.随着温度箱内部温度的变化，试样温度会相应改变.温度箱的试验温度范围为-180～300 ℃，误差为±1 ℃.考虑到试样的屈服强度较低，为准确得到试验结果，拉伸初始预紧力取为5 N.测试时下夹固定，移动上夹拉伸试样，通过夹具间位移计算应变.深圳三思万能拉伸试验机的精度为0.1%，有效拉伸距离为900 mm.通过基于标准MTS(Mechanical Testing & Simulation，力学测试与模拟)测力传感器的力传感器测量力，其精度为±1 N，量程为200 N.

2 拉伸应力-应变曲线和分析

图2所示为ECTFE薄膜的拉伸应力-应变曲线，其中σ为应力，ε为应变.图2(a)是所有温度下的应力-应变曲线，图2(b)、2(c)、2(d)分别为80、20、-50 ℃下的应力-应变曲线.可以看出，ECTFE薄膜存在着明显的温度依赖性，在曲线屈服点处开始产生细颈与剪切带，这是自由体积增加的结果.拉伸曲线后期(应变硬化阶段)，大应变区域出现明显的非透明白化现象.从热力学角度分析，温度对试样的结晶结构有一定程度的影响，温度的改变可引起链段松弛特征、松弛机理和重新排列特征的变化，尤其是在玻璃化转化温度 (Tg点) 45 ℃ 附近曲线的特征变化显著.

ECTFE薄膜的温度依赖性主要体现在主要力学参数的变化.随着温度的降低，分子链段运动受到阻碍，曲线抬高，弹性模量、抗拉强度、冷拉平均应力和屈服强度增大，断裂延伸率减小.屈服应变和屈服时间的变化在Tg点附近出现极值点，因此临界流动应力等经典屈服理论不再适用，可采用将聚合物认为是高黏度应力活化流体的分子流动理论，如Eyring理论[15]、Argon双结理论[16]，这些方法精确描述了应变速率和温度的影响，但没有考虑应变软化和应变硬化效应.

通过对比可以发现：减慢拉伸速率与升高环境温度对材料拉伸行为有相似的影响，符合时温等效原理.相比较而言，ECTFE薄膜的速率依赖性较弱，在宽广的拉伸速率内均为韧性断裂，拉伸强度远远大于屈服强度[2].然而其温度依赖性较高，由拉伸应力-应变曲线可以发现，ECTFE薄膜在低温硬而弱，在高温软而韧.温度升高，分子链段热运动加剧，促进松弛过程，材料模量和强度下降，伸长率变大，拉伸应力-应变曲线被拉长.温度过高时，材料可能发生黏性流动，断裂伸长率大，强度和弹性模量小.接近常温时强迫高弹形变充分表现，符合高聚物基本力学特征，拉伸应力-应变曲线符合高聚物拉伸的典型特征.当温度降低时，拉伸应力-应变曲线明显抬升，这是由于链段运动所产生的内力与外力作用无法协调，强迫高弹形变无法充分发展，材料屈服需要更大的外力，因此强度增加；温度过低时，强迫高弹形变来不及发生，膜材在冷拉阶段开始后断裂，弹性模量和强度大.

3 主要力学参数的温度依赖性分析

主要力学参数的取值方法参考文献[2]，如图3所示.

图3 ECTFE薄膜拉伸应力-应变曲线的4个阶段Fig.3 Four stages of tensile curves of ECTFE foil

在宽广的温度条件下，ECTFE薄膜的抗拉强度、屈服强度、冷拉应力与温度呈线性关系.屈服应变、断裂延伸率、弹性模量、断裂能与温度的3次幂函数呈较好的非线性关系.屈服时间、断裂时间与温度的逆多项式呈较好的非线性关系，在Tg点附近出现峰值点.

由于弹性模量、屈服强度、拉伸强度及韧性是工程材料重要的力学性能指标，温度对弹性模量的影响较为显著，因此在工程设计中考虑到ECTFE薄膜材料的温度相关性，可以更好确定材料在实际工程中的受力特性.此外，辅以对其他力学参数的温度相关性分析，可以确定试验的可靠性，从而通过在不同温度下的力学性能参数及其拟合公式，作为薄膜结构设计的数据支持和参考.

3.1 屈服应力和屈服应变

ECTFE薄膜在初始段的拉伸应力-应变曲线如图4所示，在所研究的温度范围内，ECTFE屈服薄膜均受单一的主链松弛所控制，次级松弛的影响较小，同时结晶程度不同，强度变化较大.

图5是ECTFE薄膜在不同温度下的屈服强度

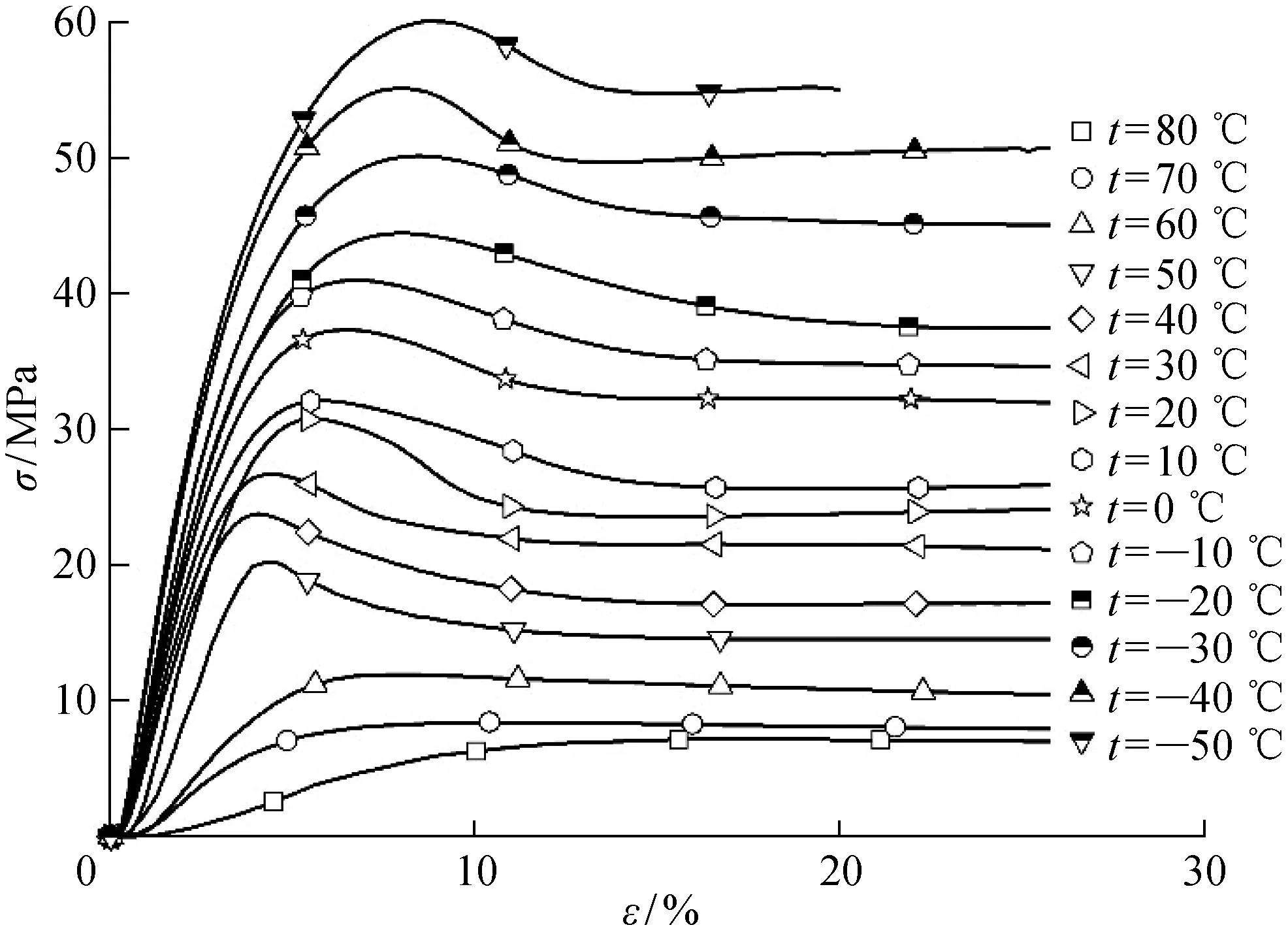
图4 ECTFE薄膜的拉伸应力-应变曲线初始段对比Fig.4 Comparison of tensile curves at initial phase of ECTFE foil

图5 屈服强度、屈服应变、屈服时间与温度的关系Fig.5 Yield stress, yield strain, and strain rate versus temperature

fy、屈服应变εy和屈服时间τy，由图可知，温度从20 ℃上升到80 ℃，屈服应力从31.465 MPa减小至6.635 MPa，降幅为78.9%.温度下降到-50 ℃，屈服强度增大至60.684 MPa，增幅达92.9%.屈服应变在40 ℃最小，为4.035%，受Tg点的影响显著.从40 ℃升温至80 ℃，屈服应变从359.3%增大至18.532%，降温至-50 ℃，屈服应变从128%增大至9.2%.屈服时间在50 ℃最小，接近Tg点，从50 ℃升温至80 ℃，屈服时间从0.947 s延长了32.3%至1.253 s，降温至-50 ℃，屈服时间从207%增加至2.907 s.ECTFE薄膜的屈服强度、屈服应变和屈服时间随温度变化的拟合方程为

图6 抗拉强度、断裂延伸率、断裂时间与温度的关系Fig.6 Tensile stress, stress at break, and break time versus temperature

fy=38.297-0.409t

(1)

(2)

(3)

3.2 拉伸强度和断裂延伸率

ECTFE薄膜的抗拉强度fu、断裂延伸率εu、断裂时间tu随温度变化的拟合方程为

fu=39.028-0.259t

(4)

εu=166.283+3.358t+0.001t2+

5.017t3+9.222t4-8.161t5

(5)

(6)

图6是ECTFE薄膜在不同温度下的抗拉强度、断裂延伸率和断裂时间，由图可知，温度从20 ℃上升到80 ℃，拉伸强度从35.02 MPa减小至19.26 MPa，降幅为45%.温度下降到-50 ℃，拉伸强度增大至55.56 MPa，增幅为59%.断裂延伸率随着温度上升而增加，从20 ℃升温至80 ℃，断裂延伸率从267.86%增至811.1%，增幅为202%，降温至-50 ℃，断裂延伸率减小了92%至20.8%.断裂时间在40 ℃最大为98.63 s，受Tg点的影响显著.从40 ℃至80 ℃，断裂时间减小至48.8 s，降幅为50.5%，降温至-50 ℃，断裂时间减小至6.4 s，降幅为93.5%.

3.3 弹性模量

小载荷下材料的行为具有线性黏弹性.温度从20 ℃上升到80 ℃，弹性模量从970 MPa减小至71 MPa，温度下降到-50 ℃，拉伸强度增大至 1 427 MPa.图7所示为弹性模量E与温度的关系.弹性模量与温度的关系式为

E=964.68+0.9t+0.126t2-

0.005t3-3.82t4+7.958t5

(7)

图7 弹性模量与温度的关系Fig.7 Elastic module versus temperature

通过分析图7可以发现，ECTFE薄膜在 40～50 ℃之间的弹性模量下降剧烈，这主要是由于该类高聚物膜材存在一个玻璃化转化点，试验测量为 45 ℃，因此从常温升温至50 ℃后，材料便从高弹态转变为玻璃态.在45 ℃以下，高聚物表现出线弹性的特征，晶区和非晶区的大分子链可以发生自由运动，材料的弹性模量较大.而在玻璃化温度以上，材料的强迫高弹形变无法充分发展，因此ECTFE薄膜的弹性模量会降低.

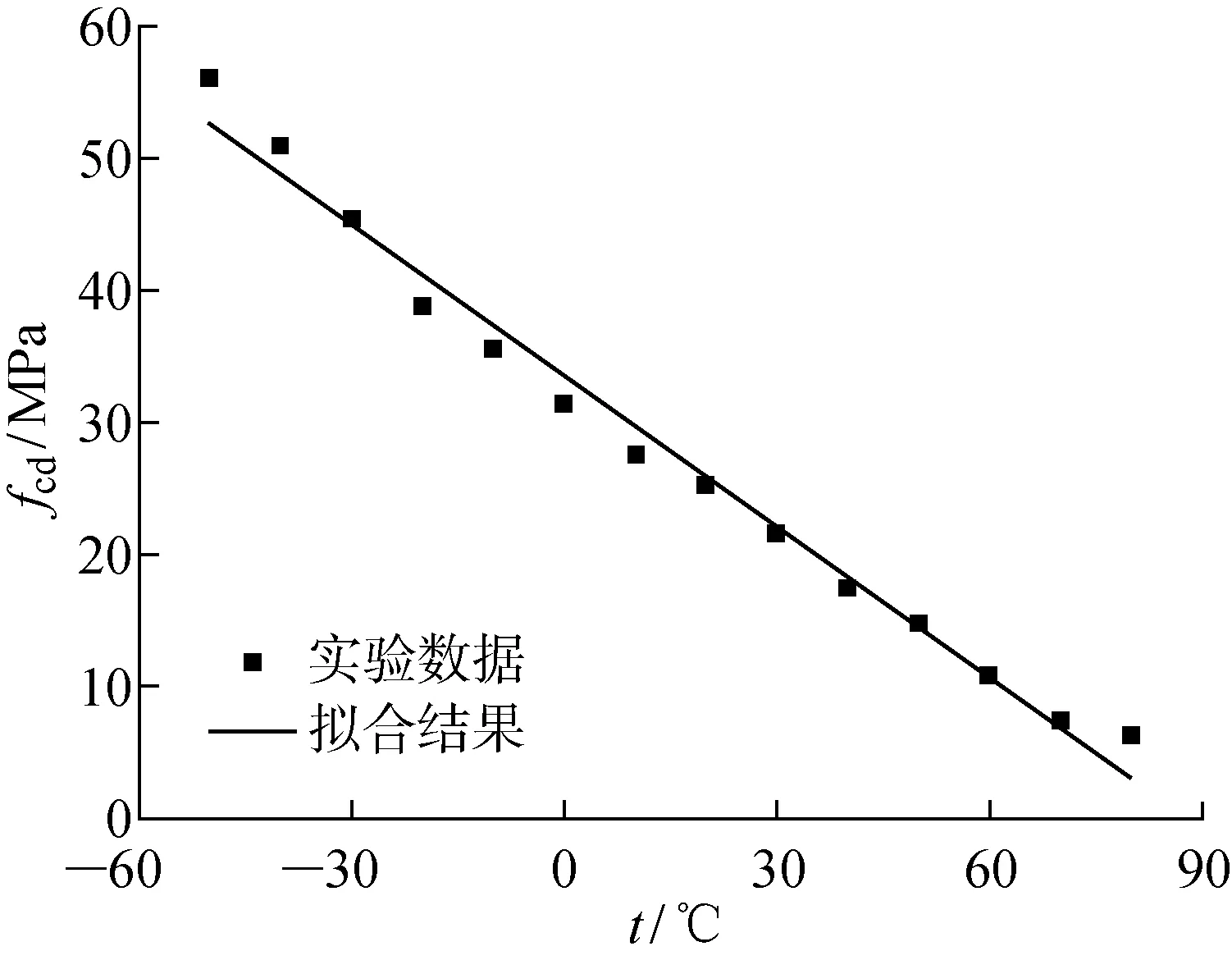
图8 冷拉应力与温度的关系Fig.8 Cold drawn stress versus temperature

3.4 冷拉应力

温度从-50 ℃提升到80 ℃，冷拉平均应力减小.从20 ℃升温至80 ℃，冷拉应力减少6.254 MPa，降温至-50 ℃，冷拉应力增大至56.098 MPa.图8所示的冷拉应力fcd与温度的关系为

fcd=33.491-0.38t

(8)

3.5 断裂能

断裂能反应了拉伸试样直至断裂所消耗的能量，可以表征材料韧性，又称应变能.温度从-50 ℃提升到80 ℃，断裂能增大，结晶度降低，材料黏性增加，塑性降低，韧度增强，这是由于分子链排列松散，孔隙率高，分子间作用减弱所致.从20 ℃升温至80 ℃，断裂能从 7 291 J/m3增大至 10 361 J/m3，降温至-50 ℃，断裂能减小至 1 033 J/m3，如图9所示，断裂能与温度的关系为

W=5 753.977+57.847t-1.684t2+

0.017t3+4.758t4-5.345t5

(9)

图9 断裂能与温度的关系Fig.9 Fracture energy versus temperature

4 结论

(1) ECTFE薄膜在宽广的温度范围内均表现出半晶高聚物的拉伸特性，出现了一次屈服现象.

(2) 弹性模量在Tg点附近存在最大切线斜率点.

(3) 随着温度的升高，拉伸应力-应变曲线整体下降并被拉长，拉伸强度、屈服强度、冷拉应力和弹性模量减小；断裂延伸率和断裂能增大；屈服应变和屈服时间先减小，在Tg点附近增加；拉伸时间在Tg点附近出现最大值；弹性模量减小.各主要力学参数与温度的多项式均呈良好的拟合关系.

(4) 本文得到的材料在不同温度下力学性能数据及评价方法，可以作为ECTFE薄膜结构设计的参考.