微结构梯度能表面振动液滴的运动特性

熊雪娇，贾志海，邓 勇，费媛媛

(上海理工大学 能源与动力工程学院， 上海 200093)

疏水和超疏水表面以其较大接触角和较小接触角的滞后特征在化工、能源、电力等领域获得了广泛应用[1].如何在工程中有效利用这些表面，进而对液滴运动进行操控也由此成为近年来的研究重点.

目前，在固体表面上操控液滴产生定向运动的方式主要有两种.① 改变表面上的微观结构以及几何参数[2-4]，如利用梯度能微结构表面进行液滴自推进[5-6]，所采用的梯度能表面结构主要有微柱状[7]、微孔状[8]、条带状[9]、球状[10]等.然而，这种单纯利用梯度能表面的方法并不能实现液滴的快速移动.② 利用外部刺激的方法促进液滴快速移动，采用的刺激方法主要有高温脉冲法[11-13]、电场法[14-15]、光化学法[16]、机械振动法[17-19]等.然而，如何有效地操控液滴运动，目前仍没有一定成法，许多方法仍处于探讨之中.

近些年来，疏水和超疏水表面在滴状冷凝传热研究中获得了广泛关注.然而，由于蒸汽冷凝形成的液滴呈现Wenzel状态，黏附力很大，冷凝液滴往往需要生长到很大尺寸才能在重力的作用下自然脱落，使得冷凝传热性能不能获得大幅提高，在蒸汽负荷较低的情况下尤其如此.所以，寻求快速的冷凝液滴脱落方法就显得至关重要.为了探讨该问题，本文尝试设计一种新型的微结构梯度能表面，并通过施加外部机械振动研究液滴在微结构梯度表面的运动特征，并在此基础上分析表面微观结构对液滴运动特性的影响.本研究对梯度能表面的工程应用以及浸润动力学理论的发展具有重要意义.

1 实验材料及方法

选用聚二甲基硅氧烷(PDMS)，采用光刻蚀技术构筑微方柱状拓扑结构.所制备的微方柱结构梯度能表面如图1(a)所示.其中：l为微方柱边长，最小微方柱边长为30 μm，相邻微方柱边长以4 μm依次递增；b=100 μm为相邻柱间距；微方柱的高度为60 μm；c=571 μm为相邻柱的距离.为了便于分析表面微观结构参数对振动液滴动态行为的影响，将表面划分为两个区域，微方柱边长l=30～294 μm的区域定义为I区(由接触角测量仪测定该区域的表观接触角θ=105°～118°)，微方柱边长l=298～566 μm的区域定义为 II 区(由接触角测量仪测定该区域的θ=118°～137°).液滴表观接触角与表面面积分数α的关系为α=l2/(lc+bc)，如图1(b)所示.由图1(b)可知，液滴表观接触角随着面积分数的增大而增大，且随着面积分数的增大，其增大幅度呈逐渐增大的趋势.

图1 梯度能表面微结构及表观接触角特征Fig.1 Schematic diagram of gradient energy surface with micropillared structure and its contact angles

实验装置如图2所示.采用平面喇叭振动膜产生的垂直机械振动作为振动源，振动频率为0～200 Hz，振幅为±2 mm.利用信号发生器和功率放大器调节振动频率和振幅，产生的正弦振动传导至液滴.采用高速摄像仪(Fastec Imaging Hispec 3)进行图像采集，采集速度为 1 000 帧/s.介质采用去离子水，实验室环境约为25 ℃，相对湿度在65%左右.

图2 实验装置Fig.2 Experimental setup

2 结果与分析

当对微结构表面施加的振动频率与液滴的固有频率一致时，两者会产生共振，此时振动台向液滴传递能量的效率最高.因此，本实验中施加的振动频率均为该尺寸液滴的固有频率.

液滴的固有频率fn为[20]

(1)

式中：ρ为液滴密度；γ为液滴表面张力；j为引发液滴的振动模式数；V为液滴体积.

固体表面的振动液滴主要存在两种形变模式[21]，即接触线固定模式和接触线移动模式.对于接触线移动模式一般存在两种情况(k=1或k=2，k为液滴初始状态与运动状态下两者轮廓线交点个数的一半)，则有：

(2)

液滴的三相接触线随振动不断变化.此时，液滴在振动模式下的节点数均为2，即k=1.由式(2)可知，j=k+1/2=3/2，进一步可通过计算获得液滴的理论固有频率.

将一个体积为12 μL、固有频率约为40 Hz的液滴轻轻沉积在微结构表面上.当对其施加40 Hz的外界振动并调节其振幅时，液滴不断产生弹性形变，但液滴的位置仍维持在原地不动.然而当振幅增加到一定阈值时，液滴虽不会脱离微结构表面，但会以蠕动的方式由面积分数较大的区域向面积分数较小的区域(从表观接触角较大的区域向表观接触角较小的区域)定向前进.液滴在区域I和区域 II 的蠕动前进特征如图3所示.

由图3可知，在振动过程中，液滴的湿接触直径d不断变化.为了表征液滴湿接触直径的变化特征，引入无量纲湿接触直径d*(d*=d/d0，d0为液滴初始状态的湿接触直径).d*随液滴运动时间t的变化情况如图4所示.结合图3和4可以看到，在振动初始阶段，液滴的接触角急剧减小，无量纲湿接触直径突然增大，这是由于加载振动后液滴由Cassie状态向Wenzel状态转变的缘故.此后，液滴向面积分数减小的方向蠕动，由于表面表观接触角逐渐减小，液滴和表面的浸润程度增大，所以无量纲湿接触直径呈逐渐增大的趋势.此外，液滴在蠕动过程中，d*随着振动不断收缩和延展，且随时间呈波动变化.随着振幅的增加，d*逐渐增大，液滴的形变程度加剧.对比I区和 II 区可以发现，随着振幅的增大，II 区的d*比I区要大.这是因为当振动能量增加时，液滴在竖直方向的形变更加剧烈，无量纲湿接触直径增大，同时在面积分数较大的区域，液滴的表观接触角增大，液滴和表面之间的初始湿接触直径较小的缘故.

图5 振动液滴滞后力的方向特征 Fig.5 Directional characteristics of vibrated droplets produced by hysteresis force

图6 梯度能表面振动液滴受力分析图Fig.6 Force analysis of gradient energy surface of vibrated droplets

根据Furmidge[22]研究， 液滴前进角余弦cosθa与液滴后退角余弦cosθr的差值反映了在水平方向由液滴接触角滞后产生的滞后力方向，其变化特征如图5所示.由图5可见，振动过程中由于滞后引起的作用力并非一直为液滴的驱动力，有时也会成为阻力.这是因为在液滴振动过程中，液滴的摇摆使得其前进角并非一直大于后退角，进而使得力的方向发生了改变.当液滴由于滞后引起的作用力和弹性形变引起的力方向一致，前进方向上的合力能够克服阻力时，液滴将会产生蠕动.此外，随着液滴向面积分数较小的方向蠕动，液滴的前进角和后退角逐渐接近，由滞后引起的作用力逐渐较小，水平方向引起的弹性力也逐渐减小，最终液滴停止蠕动.

对于初始轻轻沉积在微结构梯度能表面的液滴，液滴呈Cassie状态，液滴底部不同程度地侵入到微方柱间隙内，由此在液滴覆盖的每个间隙内均受到Laplace力的作用，如图6(a)所示.其中：Fex为液滴在水平方向产生弹性形变力；Fs为水平方向的作用力；Fvis为水平方向的黏附力；FG为液滴受到重力；FN为表面的支持力；FI为振动产生的惯性力；Fey为垂直方向上的弹性力.随着面积分数的减小，底部侵入到微方柱间隙内的深度减小，曲率半径增大，导致间隙内产生的Laplace力逐渐减小，间隙内的Laplace力如图6(b)所示.其中：Ri为陷入微柱之间液体的曲率半径；pliq为液体的Laplace压力；pg为气体的Laplace压力;θi为陷入微柱的液体的接触角.在这些力的作用下，液滴的重心产生偏移，引起液滴在水平方向产生弹性形变力Fex，进而造成液滴的前进角和后退角产生变化，即液滴水平方向的接触角滞后，并由此产生水平方向的作用力Fs.当液滴产生运动后，液滴受到水平方向的黏附力Fvis.同时，在垂直方向上，液滴受到重力FG，表面的支持力FN以及振动产生的惯性力FI.此外，由于液滴的重心发生了变化，液滴受到垂直方向上的弹性力Fey.在振动作用下，初始阶段液滴将由Cassie状态向Wenzel状态进行转变，液滴底部受到的Laplace力逐渐消失，液滴形变程度变缓，水平方向重心偏移程度减小，纵向偏移程度增大，如图6(c)和6(d)所示.其中：δx为液滴形变前后质心在水平方向的形变量；δy为液滴形变前后质心在垂直方向的形变量；O1为液滴形变前重心的位置；O2为液滴形变后重心的位置.

由图6(b)可知，对于初始沉积在表面的液滴，其陷入微柱之间液体和空气之间的Laplace压力差可表示为

(3)

式中：γL为液体的表面张力.随着液滴向面积分数减小的方向运动，液滴逐渐侵入到微结构间隙内，曲率半径Ri逐渐增大，间隙内产生的Laplace力Δpi逐渐减小，因此液滴在水平方向的形变程度减小，即液滴在形变过程中表面积变化量ΔS和液滴形变前后质心在水平方向的形变量δx减小，液滴的前进角θa和后退角θr逐渐接近.需要说明的是，随着振动过程中液滴发生向Wenzel状态的转变，底部间隙内的Laplace力消失，液滴只是在微结构表面的梯度表面能E作用下产生形变，其形变程度要比液滴发生浸润状态转变前有所减小，导致所受到的水平方向的驱动力也随之减小.

由振动台传导的能量引起的惯性力FI为

FI=ρVAf2

(4)

式中：A为振动幅值；f为振动频率.

液滴在振动过程中因形变而产生的垂直方向上的弹性力为

(5)

形变液滴的表面能变化量可表示为

ΔE=γlgΔS

(6)

式中：γlg为气液表面张力.根据式(5)和(6)可以推导出垂直方向上的弹性力Fey为

(7)

则液滴受到微结构表面的支持力FN为

FN=FG-Fey-FI

(8)

液滴在振动过程中因形变而产生的水平方向上的弹性力为

(9)

由液滴形变产生的水平方向上的作用力Fs[22]可以表示为

Fs=ψdγlg(cosθr-cosθa)

(10)

式中：ψ为滞留力系数，可由实验获取.

液滴在运动过程中受到的水平方向的黏附力Fvis为

Fvis=μFN

(11)

式中：μ为摩擦因数.将式 (8) 代入式 (11)，则有：

(12)

式中：g为重力加速度.

则液滴在水平方向的合力ΣF(以液滴向面积分数减小的运动方向为正方向)可表示为

ΣF=Fs+Fex-Fvis

(13)

将式(9)～(11)分别代入式(13)，可得

(14)

则水平方向液滴的加速度a为

(15)

式中：m为液滴质量.

根据式(14)可知，由于振动液滴的滞后力可正可负，水平方向的弹性力也可正可负，所以作用于液滴的合力也可正可负.在液滴振动的初始阶段，由于梯度表面能的作用，液滴的前进角大于后退角，滞后力大于0，且液滴水平方向形变大于0，所以水平方向的弹性力为正，导致最终作用于液滴的初始合力 ΣF>0，液滴开始以一定速度向正向开始运动.然而随着振动的进行，液滴受到的合力方向不断发生改变，导致液滴的运动速度呈波动变化.此外，随着液滴向面积分数减小的方向运动，振动液滴的形变程度逐渐减弱，液滴前进角和后退角逐渐接近，即(cosθr-cosθa)波动总体减小(见图5)，液滴表面积的变化量以及水平方向的弹性形变也逐渐减小，导致水平方向上的作用力减小，水平方向的弹性力也随之减小.在垂直方向，液滴形变程度增大，无量纲湿接触直径增大(见图4)，使得垂直方向的弹性形变增大，引起垂直方向上的弹性力减小，导致支持力增大，水平方向的黏附力增大，液滴在水平方向的合力减小，液滴加速度减小直至为0.采用式(15)进行计算，获得的理论计算结果如图7所示.

通过高速摄影仪采集到的实验图片可以获得振动液滴的运动时间，使用图像处理技术可以获得振动液滴的运动距离，由二者可计算出液滴运动过程中的速度，进而计算振动液滴的加速度(实验采用的振动频率为40 Hz，对应周期为25 ms，在加速度计算中图片之间的时间间隔为8个周期，即200 ms).由图7可以看到，液滴的加速度随振幅的增大呈递减趋势.在振动初始阶段，加速度剧烈下降而后逐渐平稳.这是因为初始时，沉积在表面的液滴呈Cassie状态，液滴受到底部的Laplace力的作用，使得液滴变形程度增加，前进角和后退角差异显著，导致水平方向的推动力增大，所以初始阶段的加速度较大.随后液滴在振动的作用下，发生由Cassie状态向Wenzel状态的转变，液滴底部受到的Laplace力消失，液滴的形变因此减弱.随着液滴向面积分数减小的方向运动，液滴的前进角和后退角逐渐趋近相同，水平方向的驱动力减小，加速度也随之减小.此外，I区的加速度比 II 区大，这是因为在I区，表观接触角的变化幅度较大，即底部受到的表面能梯度较大，液滴形变程度较大的缘故.根据图7的计算结果，理论模型值和实验结果吻合良好，从而验证了模型的正确性.

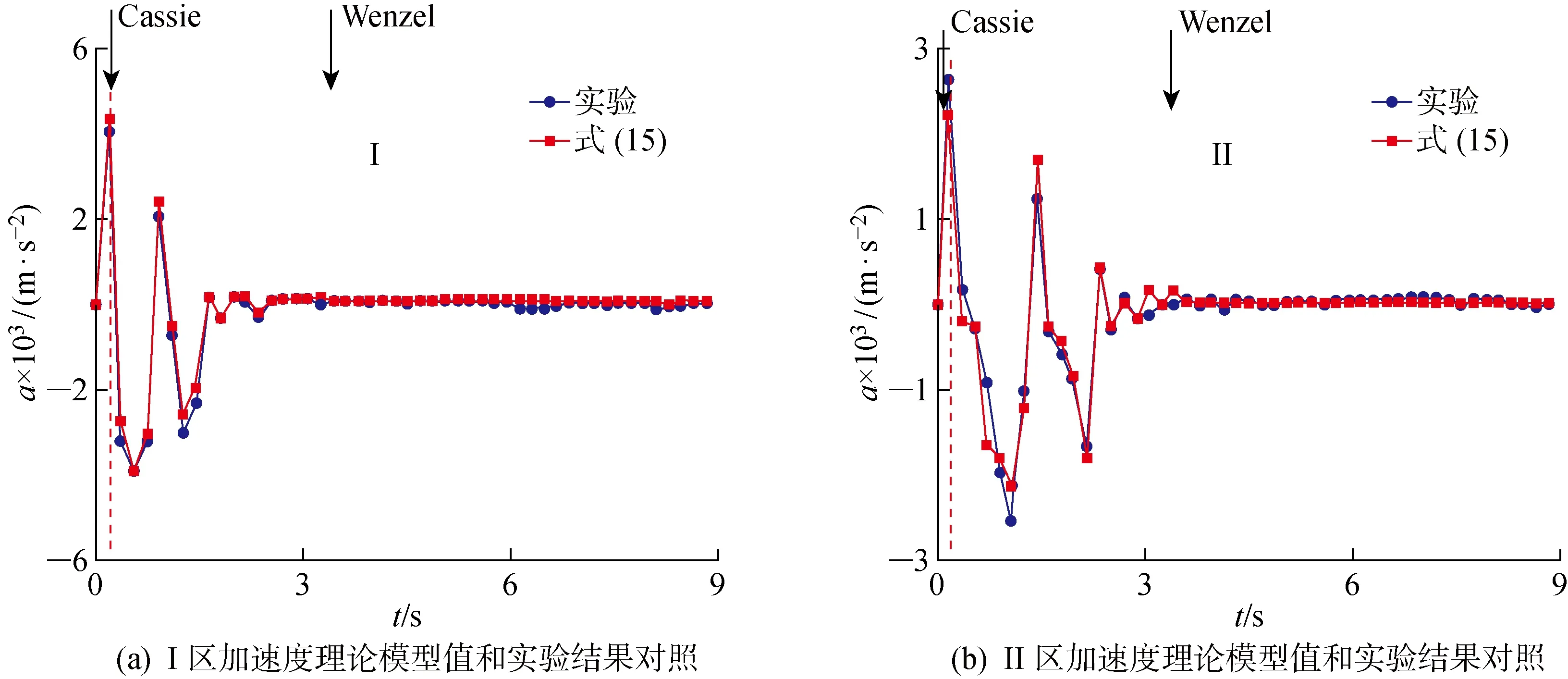
图7 振动液滴运动时的加速度特征Fig.7 Acceleration characteristics of vibrated droplets in motion

3 结论

(1) 在微结构梯度能表面，随着振幅的增加，液滴会发生由面积分数较大的区域向面积分数较小区域的定向运动.

(2) 在微结构梯度能表面，随着振幅的增加，运动加速度逐渐减小，且在面积分数更大的表面的运动加速度更小，湿接触直径变化的范围更大.

(3) 随着液滴的定向运动，液滴会发生由Cassie状态向Wenzel的浸润状态转变，底部Laplace力消失，液滴的形变程度随之逐渐减小，导致液滴受到的驱动力逐渐减小.此外，由于液滴湿接触直径的变化与浸润状态转变的影响，液滴运动所受阻力不断增加，液滴最终停止运动.

(4) 本研究为利用梯度能表面实现滴状冷凝液滴的快速脱落提供了思路，尤其针对重力影响减弱状态下，冷凝液滴不能利用重力自然脱落的情况.