钢球展开轮表面微结构几何参数优化研究
潘承怡,童圆栖,赵彦玲,李侠,曹冠群
(哈尔滨理工大学 机械动力工程学院,哈尔滨 150080)
钢球表面质量检测是轴承钢球生产中必不可少的环节。目前,捷克的AVIKO 系列钢球表面缺陷自动检测仪展开钢球的效果较好[1-2],其核心部件展开轮通过表面摩擦力将钢球全表面展开。展开轮与钢球均为镜面,在实际检测过程中,极易发生打滑现象,从而降低钢球检测效率,且展开轮因长期受到滚滑复合摩擦,导致过早磨损失效,增加了钢球的检测成本。有研究表明,表面微结构能改善材料的摩擦磨损特性和提高零部件的力学性能,国内外有许多学者对微结构的应用进行了研究[3-5]。胡天昌等[6]利用激光技术在GCr15 钢的表面进行微结构加工,使用扫描电镜观察微结构表面的磨损形貌,最终分析得出结论:干摩擦条件下,具有表面微结构的试件与表面光滑的试件相比,摩擦系数有所提高,抗磨性能更好。王丽丽等[7]在摩擦副表面加工了网状、沟槽和凹坑不同分布形式的微结构,通过摩擦磨损试验研究其减摩效果,发现与光滑表面相比,沟槽和凹坑状微结构的减摩效果更为显著,且能有效降低温升。Otero Nerea 等[8]通过在刀具表面增加微结构来降低磨损程度,从而增加刀具的使用寿命。在进行切削试验时发现,在同一工况和材料的条件下,加工有表面微结构的刀具寿命是未加工表面微结构刀具的10 倍。Y. Feldman 等[9]研究了在发动机汽缸内表面加工微结构的影响,发现在汽缸内加工微结构可以有效降低汽缸内的磨损,同时活塞环的磨损与发动机的耗油量都有所改善。
近年来,将微结构应用在展开轮表面的研究取得了一定进展。赵彦玲等[10]对展开轮表面凹坑微结构进行了试验研究,分析比较了不同形状和面积的凹坑对摩擦系数和磨损量的影响。孔泳力[11]对平面试件表面的条纹、网纹、凹坑微结构的摩擦特性进行了对比研究。孙蒙蒙[12]将展开轮简化为圆柱体试件,对圆柱体线接触表面微结构的摩擦特性进行了研究。车春雨[13]对不同载荷和微结构参数下展开轮的磨损量进行了摩擦磨损试验和数值模拟。李威[14]对展开轮不对称锥面的微结构摩擦磨损性能和展开轮寿命预测作了仿真研究。
以上研究均表明,表面微结构对提高展开轮摩擦磨损性能和寿命有显著作用,且凹坑微结构提高表面摩擦系数和降低磨损程度的效果最好,但尚未对展开轮表面增摩降磨性能最佳的凹坑微结构几何参数匹配进行优化研究。本文在物理试验和磨损数值模拟的基础上,建立了展开轮表面微结构的几何参数优化模型,并进行了多目标求解,以获得最佳增摩降磨特性的微结构几何参数匹配,从而最大限度地提高钢球检测效率,降低钢球检测成本,为微结构展开轮的设计及其在钢球表面质量自动检测仪中的应用提供方法和依据。
1 钢球与展开轮接触面积分析
展开轮表面的凹坑微结构面积取值非常重要,过小的微结构面积不足以发挥作用,而过大的微结构面积会使钢球在展开过程中产生跳动与漏检,降低钢球的检测质量。因此,需要计算工作时钢球与展开轮之间的接触面积范围,以此设计微结构面积。钢球与展开轮材料的属性见表1。采用Cr1Mo2W50 作为展开轮材料,此材料具有较高的耐磨性和弹性模量,以钴作为粘结剂金属使其具有较高的硬度。当钢球与展开轮接触时,作用力较小,因此展开轮接触表面的变形较小。在高弹性模量和低接触变形条件下,展开轮的接触变形主要是弹性变形,利用Hertz 理论可以计算钢球与展开轮之间的接触变形尺寸。

表1 钢球与展开轮的材料属性Tab.1 Material properties of steel ball and unfolding wheel
如图1a 所示,在法向载荷Q的作用下,钢球与展开轮之间的接触变形发生在接触点O 处,展开轮在接触点的曲率为R2。钢球与展开轮之间的接触为球体与锥体之间的接触,接触变形区域为不规则图形,其形状如图1b 所示。现有的Hertz 公式不能用于计算此接触变形区域的大小。

图1 钢球与展开轮的接触Fig.1 The contact between the steel ball and the unfolding wheel: a) contact model of steel ball and unfolding wheel; b) shape of contact deformation area
如图2a 所示,当圆柱体底面的半径等于展开轮锥面接触点处的曲率半径,即R2Ⅱ=R2时,球体与圆锥体之间的接触可以近似为球体与圆柱体之间的接触,接触变形面积的大小几乎相等。球体与圆柱体的接触变形区域是椭圆形的,如图2b 所示。设椭圆形接触变形区域的半长轴为a,半短轴为b,其面积为S。

图2 球体与圆柱体的接触Fig.2 The contact between the sphere and the cylinder: a) contact model of sphere and cylinder; b) shape of contact deformation area
对于球体与圆柱体的接触,可以参考球轴承中滚动体与内圈滚道的接触计算[15]。首先需要计算辅助变量cosτ:

式中:ρ1I、ρ1Ⅱ、ρ2I、ρ2Ⅱ表示接触物体的主曲率,下标1、2 分别表示两接触物体,下标Ⅰ、Ⅱ分别表示主曲率所在平面。可得R1I=R1Ⅱ,都等于钢球半径R1,R2I趋近于无穷大,因此ρ2I=0,R2Ⅱ等于接触点处圆锥面的曲率半径R2。即:

由式(3)将式(1)、式(2)化简可得:

冈本纯三对球轴承内钢球与内圈滚道的Hertz 接触问题进行了计算,得到接触椭圆长半轴a与短半轴b计算公式为[16]:

式中:Q为法向载荷;E*为综合弹性模量;μ、ν为cosτ决定的系数,根据cosτ查表可得μ=1.29、ν=0.80。其中综合弹性模量E*的计算表达式为:

式中:E1、E2分别为表1 中钢球与展开轮材料的弹性模量;υ1、υ2分别为表1 中钢球与展开轮材料的泊松比。代入式(9)计算可得综合弹性模量E*=1.62×105N/mm2。
在实际检测中,钢球与展开轮之间的载荷Q1为15~20 N[17]。由几何关系可得,钢球与展开轮在接触点处的法向载荷Q可以表示为:

展开轮能检测的钢球直径范围为 10.3188~30.1625 mm,因此钢球半径R1的范围为 5.1594~15.0812 mm。由几何关系计算可知,接触点处展开轮曲率半径R2的范围也为5.1594~15.0812 mm。将上述数据代入式(6)、(7)、(8),求得半长轴a、半短轴b和接触面积S最小与最大尺寸:amin=72 μm,amax=112 μm;bmin=45 μm,bmax=70 μm;Smin=9.8094×10–3mm2,Smax=2.4618×10–2mm2。
从上述数据可知,单个微结构面积应该与接触变形区域面积在同一数量级上,因此展开轮表面单个微结构面积取值范围为10–3~10–2mm2。
2 摩擦磨损试验
2.1 钢球-展开轮接触模型简化及试件制备
考虑到展开轮是非对称双圆锥面体,在展开轮圆锥面上激光加工微结构时,必须使用专用夹具。由于展开轮价格昂贵,在没有量产的情况下,制备微结构表面展开轮进行试验的经济和时间成本很高,因此需要对钢球与展开轮的接触模型进行适当简化,再进行摩擦磨损试验。为便于实验,将展开轮锥面沿母线扩展,形成一个封闭的圆环,并以此制备盘状试件,如图3 所示。

图3 接触模型化简过程Fig.3 Contact model simplification process
进行优化的展开轮表面微结构参数分别为形状、面积、深度和间距,每个参数设计3 种变量。若进行多种微结构参数不同匹配情况下的摩擦磨损试验,工作量过于巨大,几乎是不可能的,因此采用四因素三水平正交试验,微结构几何参数组合共9 组。微结构形状为圆形、正方形和菱形,其中菱形的锐角为60°。微结构的单坑面积依次为7.85×10–3、1.76×10–2、3.14×10–2mm2,三种单坑面积是按照当圆形微结构直径分别为100、150、200 µm 时所设计的。根据单坑面积,算出正方形微结构的边长分别为88.6、132.9、177.2 µm,菱形微结构的长/短对角线分别为164.9/95.2、247.4/142.8、329.8/190.5 µm。微结构的深度为50、100、150 µm。因为展开轮的工作表面为圆锥曲面,所以用角度θ表示圆锥面圆周方向上相邻微结构中心之间的距离,θ分别取2.5°、3.0°、3.6°。
加工后的微结构试件如图4 所示,盘状试件微结构区域到试件中心的距离l=8.3344 mm。利用超景深显微镜观测9 组试件表面的微结构,得到图5 中不同试件表面的微结构照片。

图4 微结构盘状试件Fig.4 Physical picture of microstructure disc-shaped specimen
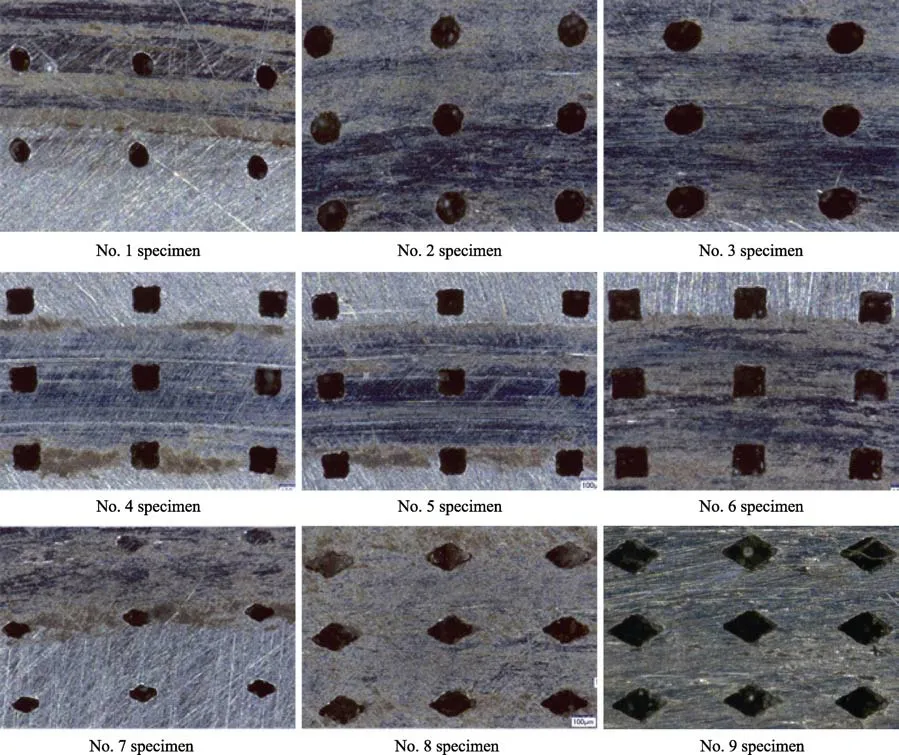
图5 超景深显微镜下不同试件表面微结构Fig.5 Surface microstructures of different specimens under ultra-depth three-dimensional microscope
2.2 试验方案及设备
根据钢球与微结构试件的接触运动状态,设计并搭建试验装置,如图6 所示。伺服电机带动试件旋转,电机转速为1500 r/min。钢球与钢球座胶接,并固定于传力杆。钢球与试件之间的运动形式为点接触滑动摩擦。考虑试验机及传感器的承载范围,采用缩小法将试验载荷定为2 N,并采用相对较长的试验时间(5 h)。在钢球座上方施加200 g 砝码,采用双面胶将砝码固定于钢球座上,以防脱落。同时打开计算机上力学传感器数据采集软件,并将数据归零,开始试验。力学传感器实时采集钢球与试件表面的摩擦力,并传送给计算机储存,所有试件均磨损5 h 后,停止试验。每组3 个试件,试验结果取平均值。

图6 球盘式点接触干摩擦磨损试验Fig.6 Ball-to-disk point contact dry friction and wear test
2.3 试验结果及分析
2.3.1 摩擦系数
该试验机采用力学传感器得到钢球与试件表面之间的摩擦力,在测试时间内,摩擦力无显著波动,同时考虑到传感器数据处理软件的存储量,因此选取中间10 min 的摩擦力数据。采用摩擦系数转换公式计算出平均摩擦系数,并将该系数作为此微结构试件表面的摩擦系数,将同一组中3 个微结构试样的平均摩擦系数作为该组微结构试样的摩擦系数。试验所得9 组微结构试件的摩擦系数见表2,并用直观分析法进行分析。

表2 不同几何参数微结构试件摩擦系数Tab.2 Friction coefficient of microstructure specimens with different geometric parameters
Rj值的大小反映该参数对摩擦系数的影响程度,数值越大,说明此参数的影响程度越大。从表2 中可以得到,微结构几何参数对试件摩擦系数的影响程度顺序为:形状>面积>间距>深度。
2.3.2 磨损质量
为确保微结构试件磨损质量测量结果的准确性,采用超声波清洗器对磨损试验前后的试件进行清洗,并烘干。采用电子分析天平测量试件磨损前后的质量,测量精度为0.1 mg。磨损质量结果见表3。
采用同样的方法对表3 中试件磨损质量数据进行分析,得到微结构几何参数对试件磨损质量的影响程度顺序为:面积>形状>深度>间距。
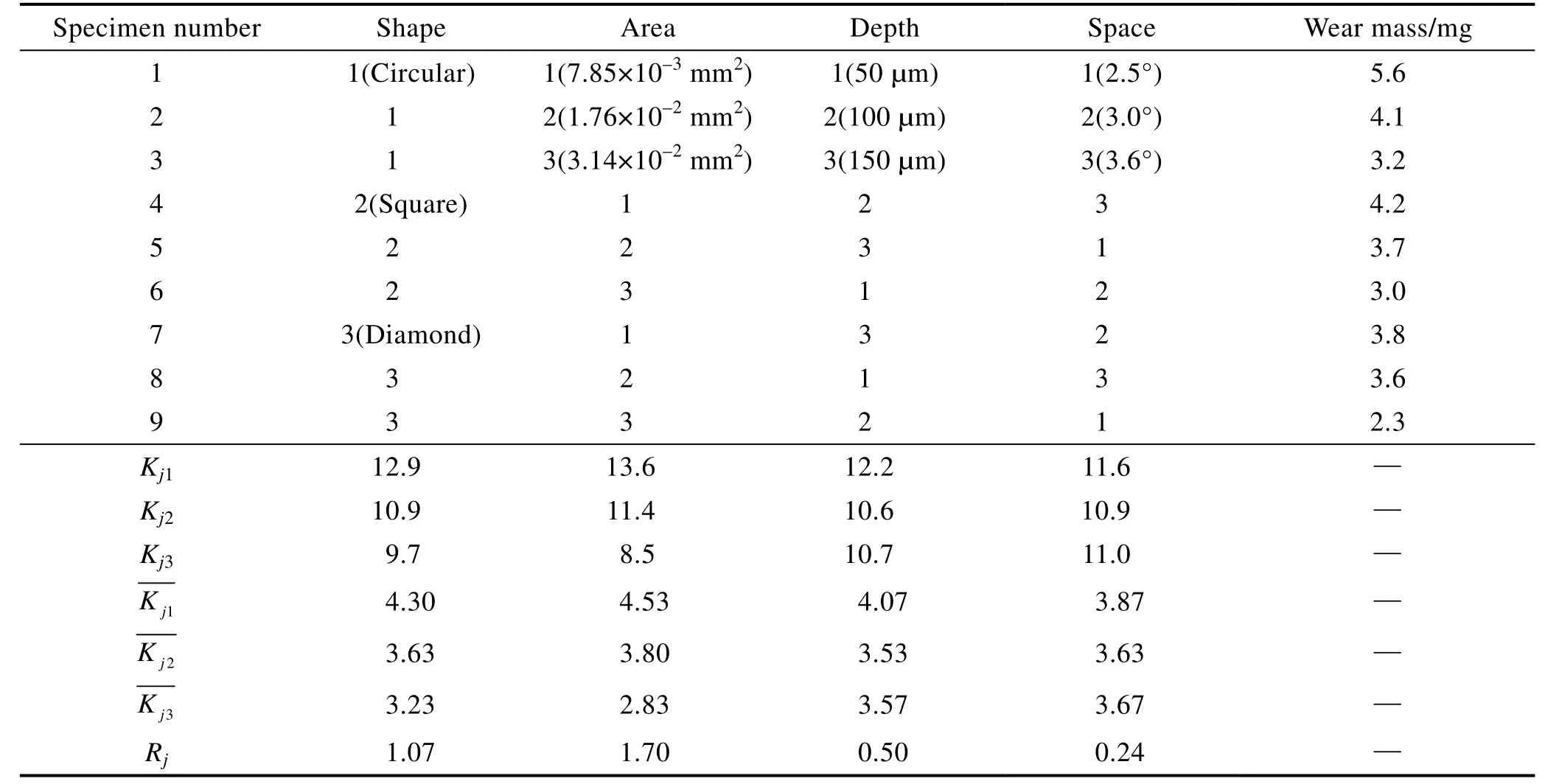
表3 不同几何参数微结构试件磨损质量Tab.3 Wear mass of microstructure specimens with different geometric parameters
3 表面微结构展开轮磨损数值模拟
3.1 基于Archard 理论的展开轮表面磨损深度计算模型
展开轮驱动面磨损后的磨损形貌放大图见图7。从图7 中可以看出,展开轮表面有清晰的凹坑、麻点和擦痕,符合粘着磨损的特征,因此展开轮表面的磨损类型以粘着磨损为主。以经典的Archard 粘着磨损模型为基础,推导微结构表面展开轮磨损深度计算公式。

图7 磨损后展开轮驱动面磨损形貌Fig.7 The wear profile of the drive surface of the unfolding wheel after being worn
Archard 磨损模型的一般表达式为[18]:

式中:V为磨损体积;L为相对滑动距离;K为磨损因子;Q为法向载荷;H为维氏硬度。钢球与展开轮之间的摩擦类型是滚滑复合摩擦,而式(11)中的L为两接触物体之间的滑移距离,因此需引入滑滚比η对滑移距离L进行修正,得到式(12)。

式中:Lg为滚动距离;η为滑滚比;dV、dLg可以表示为式(13)。

法向载荷Q可以表示为:

式(13)、(14)中:h为磨损深度;A为接触面积;σ为接触应力;vg为滚动速度;t为时间。
由式(11)—(13)可以推导出单位时间内的磨损深度表达式:

展开轮表面某一接触点处的接触应力并不是常量,而是随时间呈周期性变化的,展开轮每转1 圈为1 个周期。因此,微结构展开轮表面某一接触点处的应力是关于时间t的函数,式(15)可以表达为:

对时间进行积分,得:

对于微结构展开轮工作表面某一接触点而言,计算某一接触点在0~t时间内的磨损深度,就是计算钢球0~t时间内经过此接触点n次后的磨损深度,钢球第i次经过此接触点时的接触应力为σi,i=1,2,…,n。则0~t时间内,函数σ(t)的积分可以表示为:

根据式(18)、(19)可以将式(17)化简为:

式(20)为展开轮微结构表面磨损深度的计算公式。
3.2 钢球与展开轮有限元模型
使用三维设计软件NX.UG,对直径为16.6688 mm的钢球和与其配套的展开轮进行几何建模。展开轮表面9 种不同几何参数匹配的微结构如图8 所示。

图8 不同试验号的微结构展开轮模型Fig.8 Microstructure unfolding wheel models of different test number
将微结构展开轮三维模型导入到ABAQUS 中进行材料属性定义、接触设置和网格划分。按表1 中的弹性模量和泊松比对钢球与展开轮材料属性进行定义,其中钢球密度输入为7810 kg/m3,展开轮密度为15 630 kg/m3。钢球与微结构展开轮之间采用面-面接触,接触类型选择摩擦,摩擦系数设置与表2 中试验结果相同。之后对模型进行网格划分,单元体类型选择四面体,共划分节点数36 754,单元数为29 552。钢球-微结构展开轮的三维装配模型及有限元网格模型如图9 所示。在钢球中心施加一个始终指向展开轮中心的载荷Q1=2.828 N,即钢球与微结构展开轮一侧的接触压力为2 N。钢球绕图9b 中虚线旋转,角速度ω1设置为160 rad/s;展开轮绕y轴旋转,分析步时间长度设置为0.2 s。

图9 钢球-微结构展开轮模型Fig.9 Model of steel ball-microstructure unfolding wheel
3.3 仿真结果及分析
不同几何参数的微结构展开轮在某一时刻的接触应力云图见图10,最大接触应力值见表4。通过计算可得钢球在0.2 s 时间内以160 rad/s 的角速度旋转了5 圈,钢球总共经过标记接触点5 次,即n=5。展开轮维氏硬度H为1700 MPa,钢球与展开轮之间的滑滚比取值在0.1 左右[12],即η=0.1。点接触干摩擦情况下,磨损因子K一般取10–4~10–5[19],此处K取中间值5×10–5。将上述数据分别代入式(20),得到磨损深度的计算结果,见表4。

表4 0.2 s 时间内不同微结构展开轮的接触应力及磨损深度Tab.4 Contact stress and wear depth of unfolding wheels on different surfaces within 0.2 s

图10 不同参数微结构展开轮应力云图Fig.10 Stress simulation diagram of unfolding wheel with different parameters
Rj越大,说明该因素对磨损深度的影响程度越大。从表4 中可以看出,展开轮表面微结构几何参数对磨损深度的影响程度顺序为:面积>形状>深度>间距。微结构的面积与形状对展开轮磨损的影响较为显著,此结果与试验结果相同。将仿真所得每组模型磨损深度结果与试验结果进行对比,如图11 所示。可以看出,仿真结果与试验结果的曲线变化趋势基本一致,这表明了所建立的数值模拟用于计算展开轮微结构表面磨损的正确性,保证了后续基于磨损数值模拟结果建立展开轮表面微结构几何参数优化目标函数的合理性。

图11 仿真结果与试验结果的磨损量对比Fig.11 Comparison of wear between simulation results and test results
4 展开轮表面微结构几何参数优化
4.1 建立目标函数
首先定义形状系数c,对微结构形状进行量化,其参数关系如式(21)。

式中:s为单个微结构的面积;l为单个微结构上最远两点之间的长度。
当微结构形状设计为圆形时,l即为圆的直径d,计算得到圆形微结构的形状系数c1为0.785;当微结构形状设计为正方形时,l即为正方形的对角线长度,假如正方形的边长为a,那么其对角线长度可表示为,算得正方形微结构的形状系数c2为0.500;当微结构形状设计为菱形,且其中锐角为60°时,l即为菱形中长对角线的长度,假如菱形的边长为b,那么长对角线长度可表示为 3b,算得菱形微结构的形状系数c3为0.289。从上述数据可以发现,当形状系数满足0.289≤c≤0.785 时,形状系数的值越大,说明微结构的形状越趋近于圆形;形状系数的值越小,说明其形状越趋近于菱形。
4.1.1 以磨损深度为优化目标建立函数
磨损深度与微结构几何参数之间一般存在复杂的指数关系,因此建立磨损深度h的通用数学模型:

式中:k为与工况有关的系数;c为形状系数;s为微结构面积;d为微结构深度;θ为微结构间距;α1、α2、α3、α4为待定系数。
对式(22)两边分别取对数得:

令y=lnh,α0=lnk,x1=lnc,x2=lns,x3=lnd,x4=lnθ,则:

将表4 中微结构各参数与磨损深度数值模拟结果经过计算取对数后代入式(23),通过LINEST 函数计算可得α=(α0,α1,α2,α3,α4)T的最小二乘估计,从而建立微结构几何参数与磨损深度之间的数学模型:

利用EXCEL 软件的回归分析功能对表4 中的数据进行回归分析,得到的磨损深度方差见表5。试验次数n=9,自变量个数m=4,取检验的显著水平为0.05。因为P值小于选取的显著水平0.05,且查阅F分布表可得F(m,n–m–1)=F0.95(4,4)=6.388,此值小于统计量F,可以得出磨损深度数学模型与磨损数值模拟数据的拟合性良好。

表5 磨损深度方差分析表Tab.5 Variance analysis table of wear depth
4.1.2 以摩擦系数为优化目标建立函数
根据试验所得摩擦系数结果,采用同样的方法得到微结构几何参数与摩擦系数之间的数学模型:

同样使用方差分析的方法对摩擦系数数学模型进行显著性检验,结果见表6。P值小于选取的显著水平0.05,且查F分布表可得F0.95(4,4)=6.388,小于统计量F,得出摩擦系数数学模型与试验所得摩擦系数结果的拟合性良好。

表6 摩擦系数方差分析表Tab.6 Variance analysis table of friction coefficient
4.2 模型优化及求解分析
4.2.1 优化问题描述
1)优化变量:形状系数c、微结构面积s、微结构深度d、微结构间距θ。
2)目标函数:

3)约束条件:
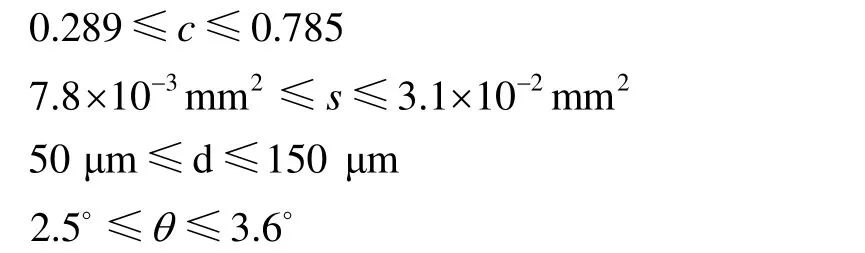
4.2.2 优化模型求解
展开轮表面微结构几何参数优化为多目标优化,由于多个目标之间相互制约,其解通常并不是只有1个最优解,而是1 个由多个非劣解组成的集合,因此采用基于Pareto[20]思想的遗传算法(NSGA-II)求解目标函数。利用MATLAB 自带的函数gamultiobj 对展开轮表面微结构参数优化模型进行求解,设置最优个体系数为0.2,种群大小为100,最大进化代数为200,利用MATLAB 软件求解后的Pareto 前沿解集如图12 所示。由图12 可知,gamultiobj 函数求解得到0.2 s 时间内微结构展开轮磨损深度h的取值范围为5.24×10–7~5.32×10–7mm,摩擦系数μ的取值范围为0.2600~0.2607。与之对应的20 个非劣解见表7。
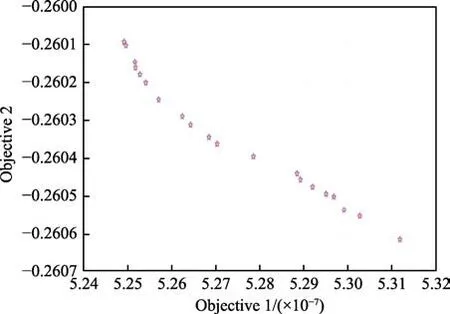
图12 Pareto 前沿解Fig.12 Pareto frontier solution
由表7 可知,非劣解的形状系数c数值在0.289左右,说明在三种微结构形状之中,增摩降磨性能最好的形状为菱形。面积s全部为0.0310 mm2,说明微结构的最佳单坑面积为0.0310 mm2。深度d为97~112 μm,大多数集中在100 μm 左右,说明微结构最优深度在100 μm 左右。间距θ在整个间距取值范围内都有分布,其中出现频数最高的为3.59°,考虑到加工与测量,将间距角度取值为3.6°。使用时,可根据具体情况,从20 个非劣解集中自行选择所需微结构参数匹配。

表7 非劣解集表Tab.7 Non-inferior solution set table
5 结论
1)对展开轮表面凹坑形微结构面积、形状、深度和间距,设计了四因素三水平正交试验。结果表明,微结构几何参数对展开轮表面摩擦系数的影响程度顺序为:形状>面积>间距>深度;对磨损量影响程度顺序为:面积>形状>深度>间距。以最大摩擦系数和最小磨损量为优化目标,获得展开轮表面微结构在可行域内的最小磨损深度为5.24×10–7~5.32×10–7mm,最大摩擦系数为0.2600~0.2607。与之对应的最佳几何参数匹配:形状为菱形,面积为0.0310 mm2,深度为100 μm 左右,间距为3.6°。
2)推导得到一种展开轮微结构表面磨损深度计算模型,将仿真结果与试验结果对比,磨损量变化趋势相同,验证了微结构表面展开轮磨损数值模拟的准确性,保证了基于数值模拟数据建立展开轮表面微结构几何参数优化模型的合理性以及求解所得最佳参数匹配的准确性。
3)微结构几何参数和摩擦系数与磨损深度之间的数学模型分别与试验结果和仿真结果数据拟合性良好,可根据微结构几何参数,直接估算出展开轮微结构表面的摩擦系数和磨损量。

