真实课堂深度学习——以“数与形”例析数学课堂的深度学习

（福州市亚峰中心小学，福建福州 350103）

教学改革多年来雷声大，雨点小，原地踏步；传统教学模式重应试，轻探究，牢不可破。教师重传授知识，轻思想方法；学生重解题技巧，轻实践应用。为了改变这种顽疾，将以教为本、以师为主教学模式让位给以学为本、以生为主的学习模式，笔者提出真实课堂，深度学习。深度学习是以真实课堂为依托，基于课堂中真实核心的问题为引领，以学生的真实探究为抓手，以知识的真实建构为依归，实现课堂的深度学习。［1］

人教版六年级上册“数与形”一课的内容核心是以数助形发现规律，以形助数解释数理，数形结合解决问题。教学目标的实现，必须让学生亲身经历真实核心问题的提出、真实的探究、知识真实的建构，才能开启数形结合之妙，体验数形结合之本，感受数形结合之广。［2］为了让学生更好地通过活动体会到数与形的完美结合，教师没有按教材原有安排进行教学。现结合“数与形”一课，谈谈如何实现数学课堂的深度学习。

一、精设计，巧引导，真问题：深度开启以数助形之妙

数形结合，一方面是以数助形，其本质是生活中“形”的问题往往蕴含着“数”的规律。让学生通过一定的观察方法，按照一定的观察顺序，经历用“数”的眼光发现和反映生活中“形”的现象，凸显用“数”解释“形”的准确、明白、入微。

在例1 中，教师先用正方形拼成的“心形”导入，并提出问题：同学们看到了哪些图形（由各种颜色的小正方形组成的“心”形）？这个图形中，用数学的眼光看到了哪些数字？让学生发现“心”中有数（红色正方形1 个，黄色正方形3 个，橙色正方形5 个，蓝色正方形7 个，总共16 个），数中有形。接着，结合核心问题，提出学习要求：你们能不能让“心”变形，摆成新的图案？要求既容易看出每种颜色的正方形各有几个，又容易看出整个图案中的正方形一共有几个。

教师组织学生利用平板动手拼摆，然后以小组为单位完成作品。有的小组按照颜色摆成“阶梯状图”（图1）；有的小组按照颜色摆成“塔状图”（图2）；有的小组摆成正方形的图，但图中各种颜色的正方形分布零乱（图3）；有的小组按“曲尺形”分颜色拼成正方形图（图4）。教师展示每个小组的作品，由小组代表汇报想法。经过汇报、追问、质疑、对比，学生发现“阶梯状图”或“塔状图”这两种摆法，虽容易看出每种颜色的正方形各有几个，但是不容易看出整个图案中的正方形一共有几个；正方形的图虽容易看出整个图案中的正方形一共有几个，但不容易看出每种颜色的正方形各有几个。学生经过尝试、调整、投票表决过程，最终明确：只有按“曲尺形”分颜色拼组成的正方形图，不仅能一眼看出有4×4=16 个小正方形，还能从中看到1、3、5、7 各种颜色的正方形块数。这样的教学在图形与数之间建立起某种奇妙的联系，使学生初步感受到1+3+5+7=16=42，逐步发现“平方数”的秘密。

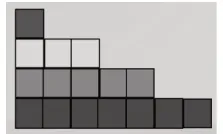
图1

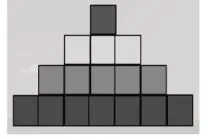
图2

图3

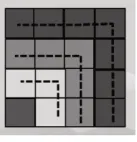
图4

最后，教师让各小组找一个自己喜欢的平方数，举例、验证、总结规律、应用。（表1）

表1

教师提出核心问题，精心组织小组合作，设计变“心”活动，引导学生通过汇报、质疑、比较，初步发现正方形总个数16（4 的平方）正好等于从1 开始的4 个连续奇数的和。大胆猜测，实验验证，自然建立起平方数和从1 开始的连续奇数的和之间的联系，实现二者的互化，深度开启以数助形之妙。

二、会观察，敢质疑，真探究：深度体验以形助数之本

数形结合，另一方面是以形助数，其本质是“数”的问题也可借助“形”的直观来解决。“数”往往是生活中的“形”的反映，所以一组数列的应用，不能只是通过化繁为简，从简单入手，发现规律，应用规律，解决问题，更需要让学生尝试用“形”的直观帮助解释“数”的本质，揭示数列的内在规律。

教师先将例2 改编为以下算式：

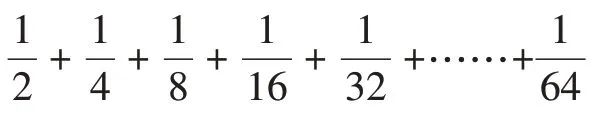
师：认真观察这组数列，有什么特征？

生1：分子都是1，后面一个数的分母都是前一个分数的分母×2。

接着，提出小组学习要求：你能利用规律，直接写出答案吗？你能解释其中的道理吗？学生独立思考，小组讨论，分工合作，然后以小组为单位完成作品并分享。

师：如果这些分数不断加下去，和会怎么样？

生：和会等于1。

师：这就是数学中常见的极值思想。其实，在学习圆面积公式转化时，也有碰到过类似现象，圆形无限切拼形成的就是长方形。

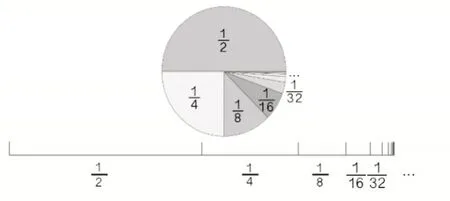
图5

通过类似的两道题目由浅入深的安排，巧妙引导学生学会从简单入手观察，发现规律，应用规律，并且学会画图来直观解释其中道理的学习方法。在学生质疑结果等于1 还是约等于1 的环节，教师主动介入，用课件直观演示+……的转化过程，引导讨论，形成了统一的意见。不仅让学生掌握解题技巧，学会借助“形”来解释“数”，渗透极值的思想，更深度体会到以形助数之本。

三、明数理，善梳理，真建构：深度感受数形结合之广

数学就是研究数与形的科学，数中有形，形中有数。华罗庚形象生动地指出二者的关系：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休。”数形结合是重要的数学思想，以形助数和以数助形就是数形结合的两个方面，以形助数更直观，以数助形更简单。［3］

例题之后，让学生做拓展提高的练习，进一步感受数形结合的好处。在这节课的尾声，教师提醒学生：“其实数形结合一点都不陌生。从一年级到六年级，大家经常使用数形结合的思考方法解决问题。”让学生畅所欲言，学生纷纷举例说明。教师实时推出整理好的数形结合的微课，帮助学生回顾各年级数形结合的典型例子，梳理、建构如下：

如一年级的退位减、进位加，借助小棒理解算理（图6）；三年级学习两位数乘两位数，借助点子图理解算理（图7）；六年级学习分数乘除法时，借助线段图，分析题目中的数量关系（图8）。数与形被看作某些几何图形中的点数的数目，成为几何和算术之间的纽带，如三角形数（图9）、正方形数（图10）（本课学习内容）、五边形数（图11）等。

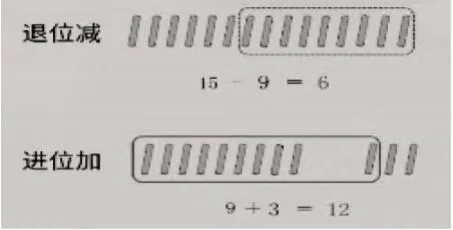
图6

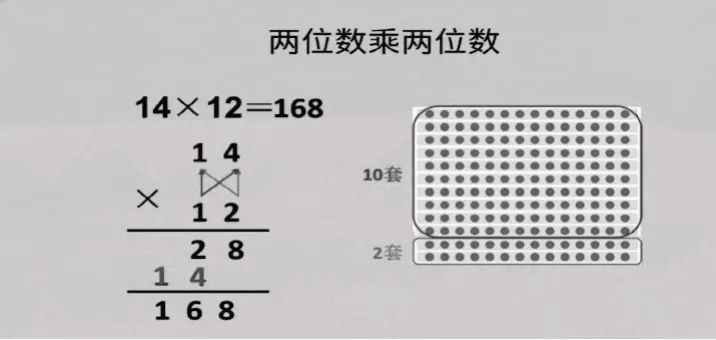
图7

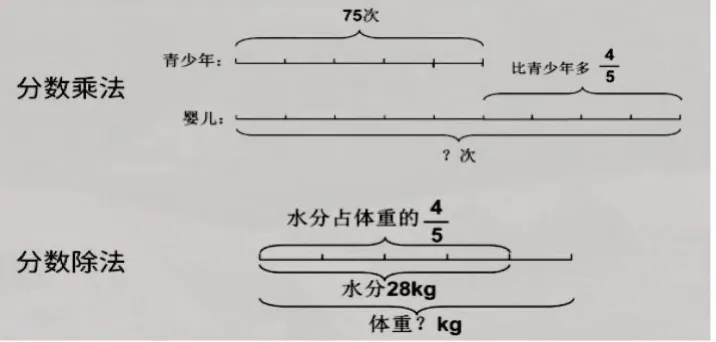
图8

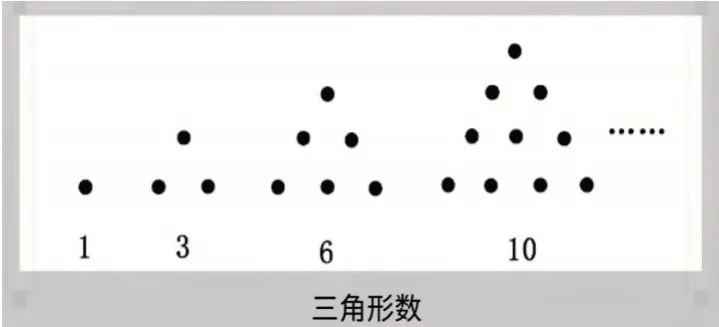
图9

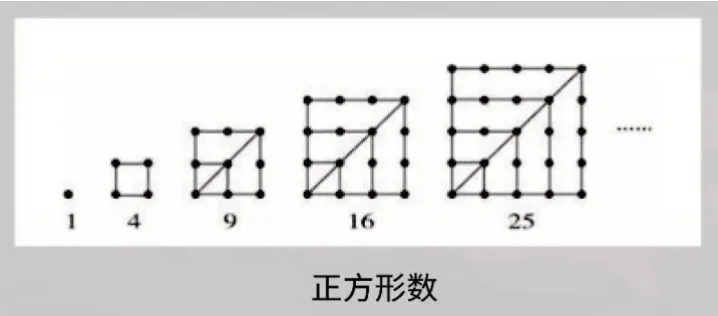
图10

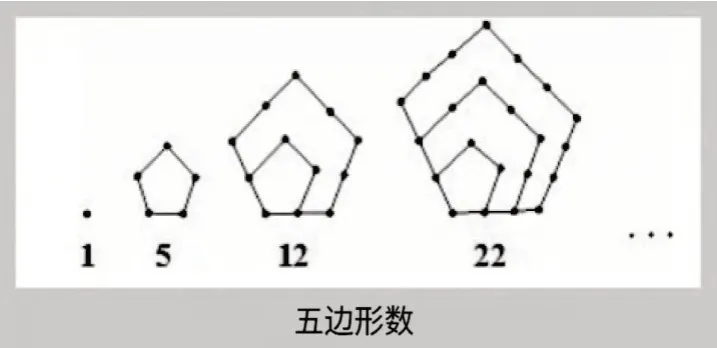
图11

教师最后总结：“历史上，数形结合一直很紧密，用几何（形）方法解决代数（数）问题，用代数（数）方法处理几何（形）问题，正是这种数形结合促进了数学的发展。在今后的数学学习中，同学们将会遇到更多精妙的数形结合的例子，比如负数、圆柱、圆锥、函数等（图12）。数学是一个精彩纷呈的广阔世界，关于数形结合的学习、探索、发现，你准备好了吗？”

数形结合在小学阶段数学教材中的渗透无处不在，但是学生未必有明确的意识。这段微课对数形结合的总结、梳理、建构，使学生明确数形结合的优势，回顾梳理数形结合的例子，真正建立起数形结合模型，深度感受数形结合之广。

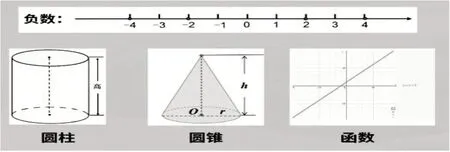
图12

总之，真实课堂是深度学习的前提，深度学习是真实课堂的归宿，两者相辅相成。要构建真实课堂，深度学习的课堂，实现以人为本，促进学生的全面发展。真实课堂与深度学习，离不开教师的精设计，巧引导，真问题；离不开学生的会观察，敢质疑，真探究；离不开课堂的明数理，善梳理，真建构。只有基于核心的问题为引领，以学生的真实探究为抓手，以知识的真实建构为依归的真实课堂，才是真正的深度学习。