数形结合 培养小学生的数学推理能力

周小青

推理能力是《义务教育数学课程标准（2011年版）》中的核心概念，是数学核心素养的重要内容。发展学生的推理能力是数学教学的重要任务，应贯穿于整个数学教学过程中。教学中，要让学生经历观察、实验、猜想、证明等数学活动过程，发展学生的合情推理能力和初步的演绎推理能力，并能有条理地、清晰地阐述自己的观点。

一、以“形”促“观”：培养学生推理能力的前提

推理是由此及彼的推演过程，没有观察就没有办法了解“此”与“彼”之间的关系，就谈不上推理。因此，观察是推理的重要前提。通过观察找到“此”与“彼”的关系并进行推理，直观图是一个很重要的载体。教学中，要通过直观图的“形”，促进学生更好地观察，使其将抽象的知识和关系直观化，并用直观图进行表示。这样，学生就能在直观观察中发现问题，引发思考，从而培养推理能力。

如教学“植树问题”一课时有这样一道题：在全长20米的小路一边植树，每隔5米栽一棵，一共要栽多少棵？教学中，可以先让学生画图表示如何栽种，并写出答案。然后，引导学生观察和思考他们得出的三种种法有什么相同与不同，并提问：“你能利用图示来解释为什么只栽一端和两端都不栽的列式依据吗？”学生借助图，从上往下观察（也可以从下往上观察），很快发现树与间隔的关系，利用间隔与树的一一对应关系解释三种不同种法的列式道理。最后，引导学生在观察的基础上进行比较，从相同处发现规律，从不同中找本质区别， 引发思考。学生就会明白：观察时要注意方法，做到有序观察，有重点地观察，多角度地观察。这样，学生在观察中获得了丰富的感知，为推理做好了准备。

二、以“形”促“思”： 培养学生推理能力的保障

数学知识的本质既表现为隐藏在客观事物背后的数学知识、数学规律，又表现为隐藏在数学知识背后的本质属性。学生只有将数学知识真正内化为自己的认知，才能完成由“此”及“彼”的推理过程。由此可见，围绕核心问题进行数学思考是学生推理的保障。教师可以把抽象的数学知识借助图形变得直观，激发学生的思考，让思考有目的、有对象、有方向，从而找到知识间的本质联系。

在“长方体体积”一课的教学中，我提出了以下核心问题引导学生思考：回忆一下长方形面积计算公式是如何推导的？长方体体积我们该怎样进行探究？长方体的体积会是怎样的？

当学生建议也可以用拼摆的方式来推导出长方体的体积时，我顺势出示几个相同的小正方体组成的长方体，学生借助直观图猜测、推理出了长方体的体积等于长×宽×高。如何验证用经验推断出的结论是否正确？学生有了不同的验证方法：

（1）利用手中的长方体再次摆一摆，通过观察记录和计算，发现：每排的数量×排数×层数=小正方体个数。也就是：长×宽×高=长方体体积。

（2）借助直观图，可以看成长方体是多个相同的长方形叠加在一起，由长方形的面积就是面积单位的累加类比推理出长方体的体积是体积单位的累加，从而推导出长方体的体积=长×宽×高。

这两种方法都利用直观图让长方体体积计算回到了源头，抓住了长方体长、宽、高与体积之间的关系。这个过程中利用演绎推理进行验证，都触及本质联系，都是在于让学生利用直观图形启发思考：是什么？为什么？循着问题一步一步完成推理，培养了学生的归纳推理能力。

三、以“形”促“说”：培养学生推理能力的关键

语言表达使图形语言过渡到符号语言，有了清晰的语言表达，才能进一步提炼为符号语言。通过语言表达把数学本质关系显示出来，这是数学推理的关键。在数学的教学活动中，要把数学结论与证明数学结论有机结合，让学生更好地感悟逻辑推理的形式和道理，在感悟的基础上积累数学思维的经验，逐步形成个性化的、合理的思维模式。

以“形”促“说”重在思维的外显性，重在表达学生自己的思考过程、推理过程或揭示数学内在的规律等，重在质的分析。表达时，可借助图形的直观来理清思路，也给听者直观的表象。如两位数乘一位数（进位）16×3，我先让学生借助具体操作表达抽象的竖式计算，学生边操作边把计算的每一步过程表达出来：先算6×3等于18，个位写8，向十位进1，3个十加上1个十，有4个十，十位上写4，所以16×3等于48的推理过程。接着，重点提问：为什么十位是4而不是3？让学生借助图说清算理，从而突破进位的难点。

推理的本质是关系的表达，找到本质联系，推理就水到渠成。因此，教师要加强学生以“形”促“说”的训练，说的过程要凸显思维的过程，重视思考问题的表现方式，让学生能有序地、较为严谨地表达逻辑关系。

四、以“形”促“构”：培养学生推理能力的途径

这里的结构一方面指的是数学知识具有结构性，是各个组成部分的搭配和排列。另一方面也指学生作为学习的主体，在学习过程中有自己的认知结构。数学学习过程是一个螺旋式上升的过程，前后知识彼此间紧密联系，有一張严密的整体结构网。如何找到知识之间的联结点，形成关系网，外显新知识的本质属性，是促进学生推理能力发展的重要途径。直观图犹如支架，能帮助学生顺利找到联结点，进行推理;经过推理后获得的新知识又纳入新的知识结构网中，让学生不断完成同化和顺应的过程。

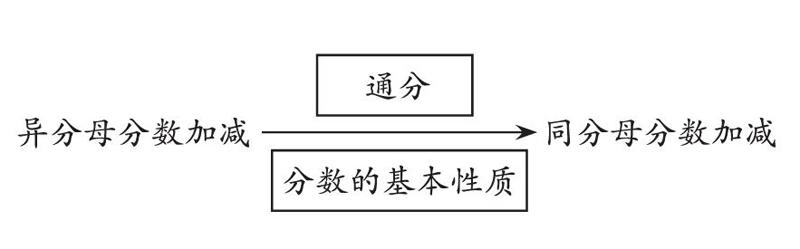
如在“异分母分数加减法”一课中，可以围绕“异分母分数如何计算”“为什么这样计算”这两个核心问题进行教学。先利用直观图，让学生理解每一份大小不相同无法直接相加减的道理。如何做到每一份大小都相同呢？学生提出借助通分，就可以把异分母分数变成了同分母分数，因此利用如下这个简单明了的结构图，就能很清晰地看出异分母分数与同分母分数的联结点：通分（分数的基本性质），就可以变成同分母分数加减。把异分母分数加减通过顺应（通分）纳入到同分母分数的知识结构中，让新知变得简单，符合学生的认知特点，与学生的认知结构联系起来。

简单明了的结构图示，不仅揭示了新旧知识的关系，也显示了借助联结点进行推理的过程与方法。

学习是一个不断经历“问题—探究—解决”的过程，这个过程往往要由推理来完成。而数学的抽象性需要借助“形”的直观来帮助理解，只有找到已知和未知的内在联结点，才能让学生真正做到知其然并知其所以然，逐步形成推理能力及数学核心素养。

课题项目：本文系福建省教育科学“十三五”规划课题“培养小学生科学归纳推理能力的教学研究”阶段性成果之一。课题编号：FJJKXB19-452。

（责任编辑：杨强）