政府科技经费投入、研发规模与高校基础研究科研产出的关系——基于省际面板数据的门槛回归分析

张宝生，王天琳，王晓红

(1.哈尔滨师范大学管理学院，黑龙江 哈尔滨 150025；2.哈尔滨工业大学管理学院，黑龙江 哈尔滨 150001)

0 引言

高等院校是创新人才与前沿技术的集聚地，是国家科技创新体系的重要组成部分和建设创新型国家的重要载体[1]。高校作为研发和创新活动的主要执行主体，近年来我国政府对高校科研投入呈现不断增加趋势，但从全局看，高校科研投入力度与科技产出并不协调[2]。在国家区域发展不平衡及科研资源有限的条件下，如何破解高校科研过程的瓶颈和障碍，协调科研投入和产出之间的关系，提升高校科研效率是政府和高校管理研究者关注的重要课题[3]。科研活动和产出根据研究性质的不同可以分为三大类，基础研究的特点是探索未知，成果主要是科学论文；应用研究得到的是技术原理、方法等，主要成果是专利；试验发展研究得到的是技术改进等[4]。高校获取的科技经费投入主要来源于政府科技拨款和企事业委托高校研发经费，其中企事业单位和高校的合作主要是从事应用研究和实验开发研究[5]。基础研究是创新的源泉，是原始性创新能力和积累智力资本的关键[6]。但是基础研究成果的公共产品属性明显，存在正外部性和市场失灵状况，需要政府支持和引导[7]。

我国科研资源的分配问题主要还是由政府来主导，政府科研投入和研发人员规模对高校研发活动、知识成果产出起到关键性作用，相关学者对此展开研究。Barro提出的内生增长理论模型指出政府科研投入是促进经济增长的重要内生动力，强调科技创新与经费投入间的关系[8]。Agasisti等指出影响高校科研投入产出效果的主要因素是高校的科研规模效率，效率低的高校科研规模扩大后反而降低了科研效果[9]。谈毅等运用多元线性回归将全国高校按照学校类型进行分类，指出政府科技投入对科技产出存在正相关关系[10]。李维春等运用面板数据模型从长期与短期角度分析科技投入与高校创新产出之间波动关系，并分析省域间存在的差异[11]。李晋等指出政府R&D投入对专利申请影响最为显著[12]。陈贤平运用门限模型指出政府科技投入对高校科技产出存在非线性影响关系[13]。郭江江指出高校科研投入并不能完全体现出对科研产出的促进作用，不同的投入指标会掩盖其投入规模的缺陷与不足，地区间经济差异和技术差异也会带来不同的影响效果[14]。

相关研究为本文奠定了研究基础，但相关研究多是从单一投入的总量上来度量，总量指标会掩盖不同研发资源的结构与特征，并不能完全反映投入产出的影响作用。政府投入科技经费作为财政资金相对可控，其对高校科研发展的效果是科研管理部门关注的重点，研究选取政府科技经费投入和研发人员规模作为衡量高校基础研究产出的核心解释变量，选取政府科研投入强度和人均政府科技经费能够反映出结构和资源匹配的相对性指标作为门槛变量，研究高校科研投入与科研产出间的非线性关系。

1 模型设定、变量与数据

1.1 门槛回归模型

(1)面板模型的构建。研究讨论政府科技经费投入、研发规模和基础研究科研产出的非线性关系，传统上讨论变量之间非线性关系，主要通过在面板回归模型中引入二次项与交互性，但容易使模型存在共线性且不能检测出结构突变点，导致估计结果与实际出现偏误。研究将相关数据进行面板处理，进而对其进行门槛回归，门槛回归的优点在于能够从样本数据中搜索其门槛值，并通过门槛值划分出合理区间，最后通过对建立的模型进行回归检验，从而判断门槛回归模型下自变量对因变量的非线性影响关系[15]。

单门槛回归模型公式为：

yit=μi+β1xit·I(qit≤γ)+β2xit·I(qit>γ)+eit

式中，下标i与t分别代表截面个体与时间，yit代表被解释变量，μi代表个体固定效应项，xit为核心解释变量，qit代表门槛变量，γ代表门槛值，I代表示性函数，当qit≤γ时，I=1，否则I=0，eit代表残差项。

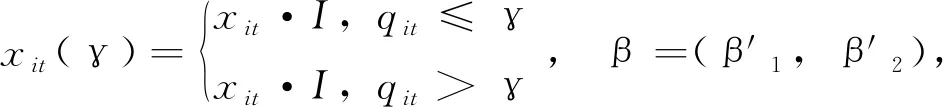
(2)面板门槛模型的估计。Hansen提出，对门槛回归模型进行估计，首先可以通过消除个体固定效应项μi，在时间维度t上计算截面内个体均值，门槛回归估计模型为：

对于给定的门槛值γ，可通过OLS方法得到参数估计值：

其中，残差平方和为：

(3)门槛效应检验。通过以上数据模型可以得出参数估计值，将门槛估计值与真实值对比，判断二者是否一致，对门槛数量、门槛效应显著性、门槛置信区间与门槛回归系数进行检验。门槛模型下LR统计量为：

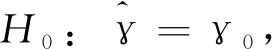
门槛估计值对应的置信区间是LR统计量小于特定要求水平下的临界值所对应的门槛区间，当LR=0时，所对应的值即为门槛估计值：

多重门槛模型可以通过以上方法进行设定、搜索与检验。

1.2 变量选取、样本及数据整理

知识生产和原创性成果多以科技论文的方式进行传播，基础研究成果的主要特点是探索未知，学术界的基本共识是基础研究的科研产出主要是科技论文[16]，但同样数量的论文可能在质量上存在巨大差异，需要综合考虑论文的质量，因此研究没有采用发表论文总数，而是采用国外及全国性刊物发表论文数作为被解释变量；政府科研投入以政府科技经费拨款指标衡量，研发人员规模以研究与发展人员全时当量指标衡量，作为核心解释变量；以企事业单位委托经费、研究与发展项目数和研究与发展项目参与研究生数作为控制变量。从科研经费来源结构角度考虑，选取相对数指标政府科研投入强度，即政府科技投入经费占高校科技经费总额的比例作为第一个门槛变量；从资源和人员匹配角度考虑，选取人均政府投入科技经费作为第二个门槛变量。

构建面板门槛回归模型如下：

模型Ⅰ：PAPit=ui+β1GIit·I(q1it≤γ1)+β2GIit·I(γ1γ2)+β4NGSit+β5EIit+β6NRDPit+εit

模型Ⅱ：PAPit=ui+β1RDPit·I(q2it≤γ1)+β2RDPit·I(γ1≤q2it≤γ2)+β3RDPit·I(q2it>γ2)+β4NGSit+β5EIit+β6NRDPit+εit

本研究数据来源于《高等学校科技统计资料汇编 (2011—2018年)》，选取2010—2017年中国30个省 (市、自治区)高校共计240个样本 (除西藏外)，变量描述性统计见表1。

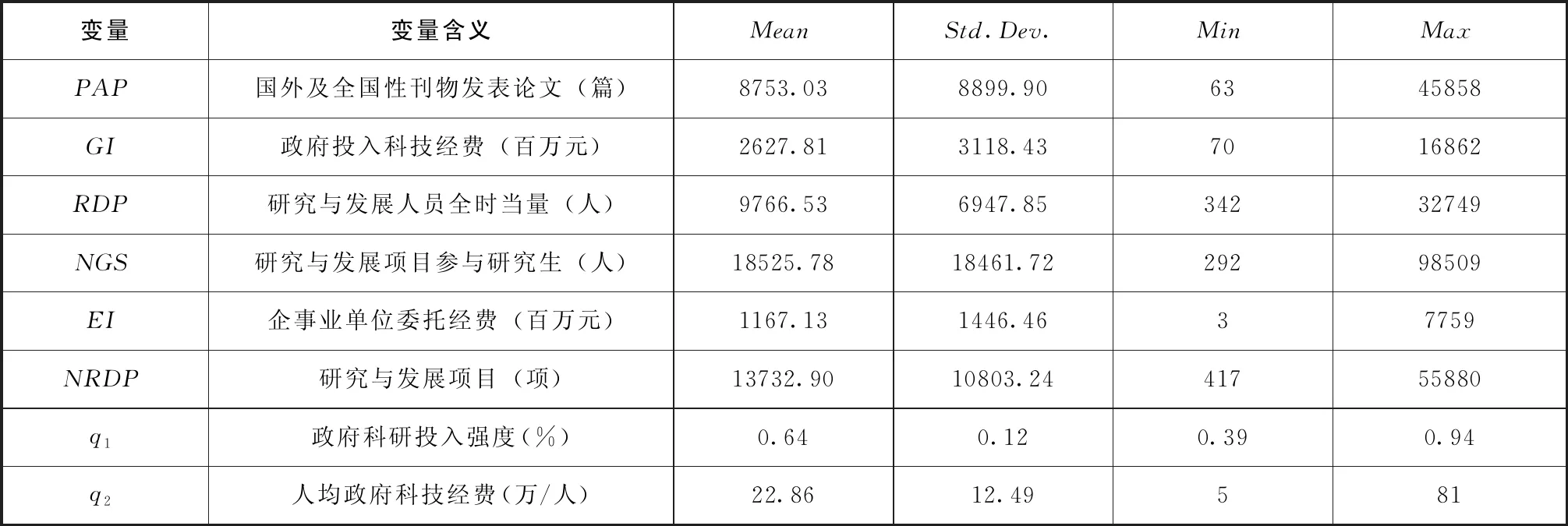
表1 变量描述性统计分析

2 门槛回归与结果分析

2.1 门槛效应与门槛值

(1)Hausman检验。通过Hausman检验确定设定模型符合固定效应模型或是随机效应模型，Hausman检验结果见表2。Hausman检验结果P<0.05，因此拒绝原假设，即拒绝随机效应模型，选用固定效应模型进行估计。研究的数据集为总体数据而非样本数据，也符合数据总体规则。

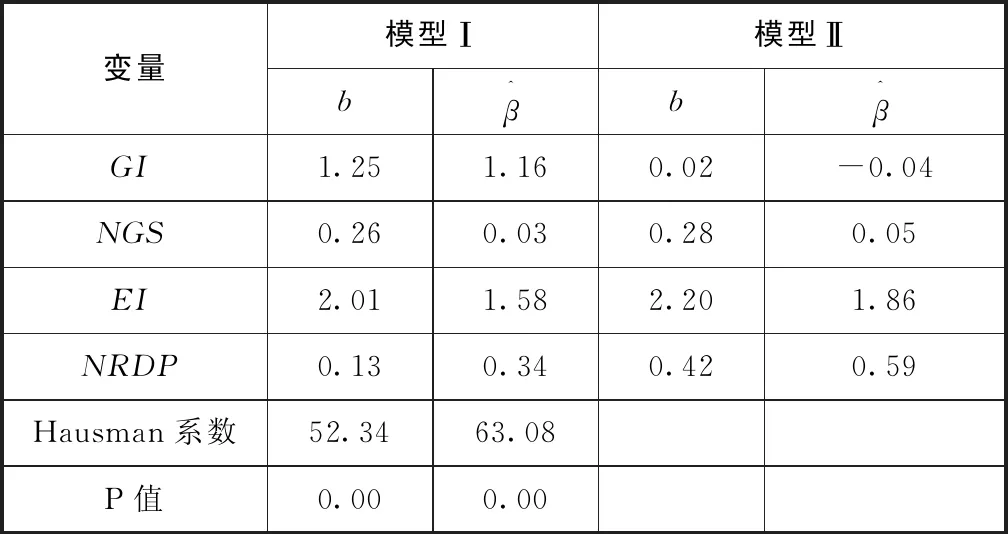
表2 Hausman检验结果

(2)门槛效应检验。应用Stata15.1将数据整理成面板数据，通过门槛自抽样验证是否存在门槛，并筛选出固定门槛值，以保证模型检验的准确性。门槛检验结果见表3。由表3可知，在模型Ⅰ中，双重门槛F值为5.937，在10%的水平下显著；在模型Ⅱ中，双重门槛F值为48.858，在1%的水平下显著，两个模型均通过了双重门槛模型的检验，说明政府科研投入和研发人员规模对高校基础研究科研产出具有双重门槛效应。

(3)门槛估计值。在模型检验结果存在双重门槛的基础之上，确定门槛估计值及其置信区间，结果见表4。由表4可知，模型Ⅰ中，政府科研投入强度的双重门槛估计值分别为0.54、0.71，分别位于[0.45，0.93]、[0.65，0.72]的置信区间之内；模型Ⅱ中，人均政府科技经费的双重门槛估计值分别为15、42，分别位于[11，37]、[42，43]的置信区间之内。

确定模型门槛值后，通过似然比来构造 “非拒绝域”，检验门槛估计值与真实值的一致性，可以看出门槛估计值有效，如图1和图2所示。

表3 门槛检验结果

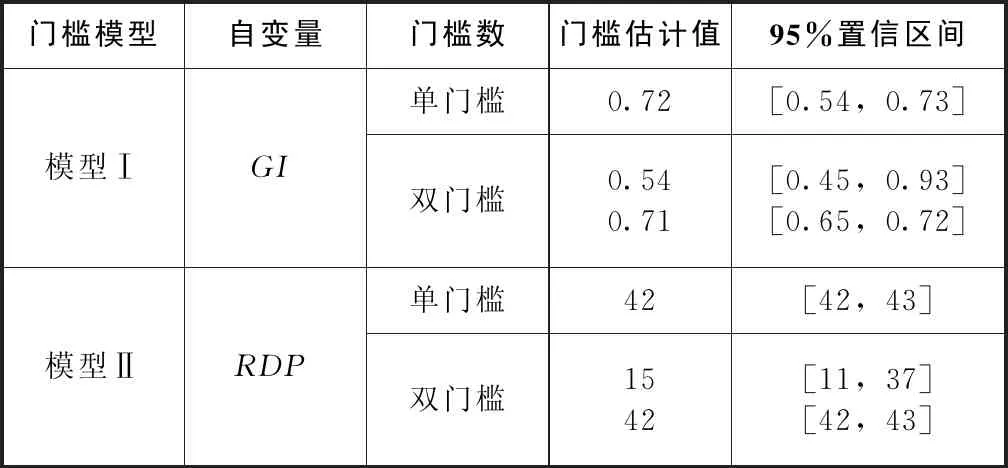
表4 门槛估计值与置信区间

2.2 模型Ⅰ的结果分析

对政府投入科技经费和高校基础研究科研产出的关系模型进行参数估计，各解释变量回归系数与稳健性标准误差估计见表5。基于政府科研投入强度的双门槛效应，政府科技投入经费与基础研究科研产出之间存在显著的非线性关系。模型的拟合优度R2分别为0.799，表明模型较好地解释了这种非线性关系。

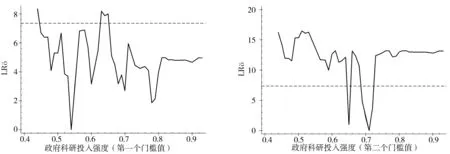
图1 政府科研投入强度门槛值LR图

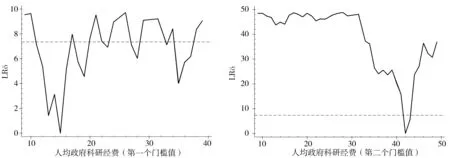
图2 人均政府科技经费门槛值LR图

模型Ⅰ的回归结果显示，当政府科研投入强度小于54%时，基础研究产出的回归系数为 -0.279，在10%的水平上显著，说明政府科技经费投入对高校基础研究产出的积极作用并没有得到体现，相反有一定的负向作用；当政府科研投入强度为54%～71%时，系数为1.800，在1%的水平上显著，转为正向作用并有较大幅度的提升，政府科技经费投入对高校基础研究产出的促进作用得到显著体现；当政府科研投入强度大于71%时，系数为-0.548，在1%的水平上显著，说明当政府投入强度过高，政府科技经费投入对科研产出呈现负向影响作用。政府科研投入强度并非越高越好，存在对基础研究科研产出的最优促进区间。

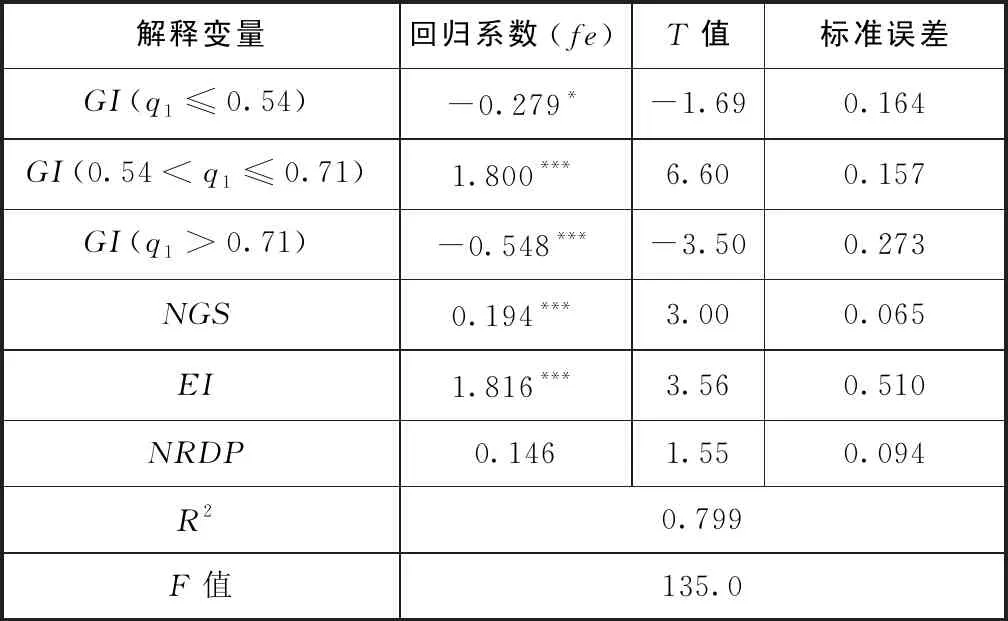
表5 模型Ⅰ回归估计结果

在政府科研投入强度处于低水平时 (低于第一门槛值)，从高校经费来源结构可以看出，横向经费占较大比重，高校科研活动主要是与企事业单位合作的应用型研究；此外基础研究对硬件条件和实验室建设的要求相对较高，而这部分投入对政府科技经费的依赖较强，因此在这一阶段高校主要处于科研基础设施条件积累阶段，真正用于科研活动的资源有限，较低的政府科技经费投入水平对基础研究有负向抑制作用。在政府科研投入强度达到一定水平时 (处于第一门槛和第二门槛之间)，高校资源配置的规模、来源和结构都处于最优阶段，政府科技经费投入对高校基础研究的积极促进作用充分显现，并出现较高的跳跃值。当政府科研投入强度过高时 (高于第二门槛值)，会导致高校科研活动对政府依赖程度过大，科研经费来源单一，高校科研活动的产学研结合不紧密，反而会对基础研究产生一定的负向作用；此外政府科研投入也需要高校科研水平的支撑，过高的科研投入强度对于实力和层次有限的高校会产生投入冗余的天花板现象。

2.3 模型Ⅱ的结果分析

对研发人员规模和高校基础研究科研产出的关系模型进行参数估计，各解释变量回归系数与稳健性标准误差估计见表6。基于人均政府科技经费的双门槛效应，研发规模与基础研究科研产出之间存在显著的非线性关系。模型的拟合优度R2为0.793，表明模型较好解释了这种非线性关系。

模型Ⅰ的回归结果显示，当人均政府科技经费小于15万元时，基础研究产出的回归系数为 -0.143，在1%的水平上显著，说明研发人员和基础研究产出为负向关联，呈现出消极作用；当人均政府科技经费在15万～42万元时，系数为0.043，转为正向作用，但并不显著；当人均政府科技经费大于42万元时，系数为0.233，呈现出较强的正向作用，在1%的水平上显著，说明在人均政府科技经费的保障下，研发人员规模效应可以得到充分发挥，对科研产出产生较强的促进作用。研发规模需要科技经费的匹配和保障，存在发挥研发人员作用的人均政府投入经费门槛。

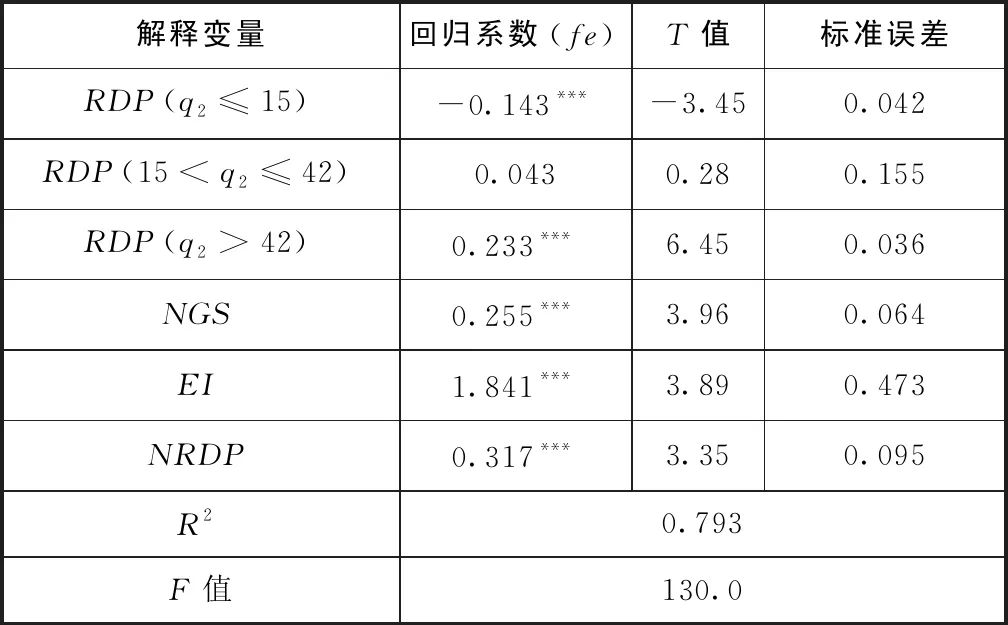
表6 模型Ⅱ回归估计结果

在人均政府投入科技经费处于低水平时 (低于第一门槛值)，在有限资源约束下，研发人员的作用并不能得到发挥，相反会进一步稀释资源，难以满足科研活动的基本保障，因此会对基础研究起到消极抑制的作用。在人均政府科研经费递进到一定水平时 (处于第一门槛和第二门槛之间)，科研资源和资本积累得到一定改善，但尚未达到合理配置，研发规模对基础研究转为不显著的正向作用，科研投入存在一定的风险性和不确定性。当人均政府投入科研经费得到充分保障时 (高于第二门槛值)，研发人员作用得到充分释放，科研活动全面增加，规模效应显现，对基础研究产生显著的推动作用。

3 政府科技经费投入和高校研发规模的实证分析

3.1 整体趋势分析

我国政府对高校的科技经费整体投入规模和强度的状态和变动趋势如图3所示。由图3可知，整体上看，2010—2017年我国政府对高校的科技经费投入规模和强度均处于逐年递增的状态，政府对高校的科研投入力度不断加强，政府科技经费投入从565亿元提高到1133亿元，年均增长10.44%；投入强度从62%上升至67%，各年份均处于对基础研究产出的最优促进区间，解释了这一时期我国通过高强度的科研投入使基础研究得到快速发展。

图3 2010—2017年政府对高校科技经费投入趋势

我国整体研发人员规模和人均政府投入科技经费的状态和变动趋势如图4所示。由图4可知，整体上看，2010—2017年我国高校研发人员规模和人均政府投入科技经费均处于稳步提升的状态，研发人员规模从26万人上升至33万人，年均增长3.29%；人均政府科技经费从17万元/人提高到31万元/人，年均增长8.52%，处于对基础研究产出促进作用不显著的次优区间，表明这一时期研发人员的规模效应并未充分显现，科研活动人员和资源的匹配程度存在优化空间。

3.2 门槛变量的区间描述性统计

对我国高校2017年的政府科技投入强度和人均政府投入经费进行区间描述性统计，见表7。

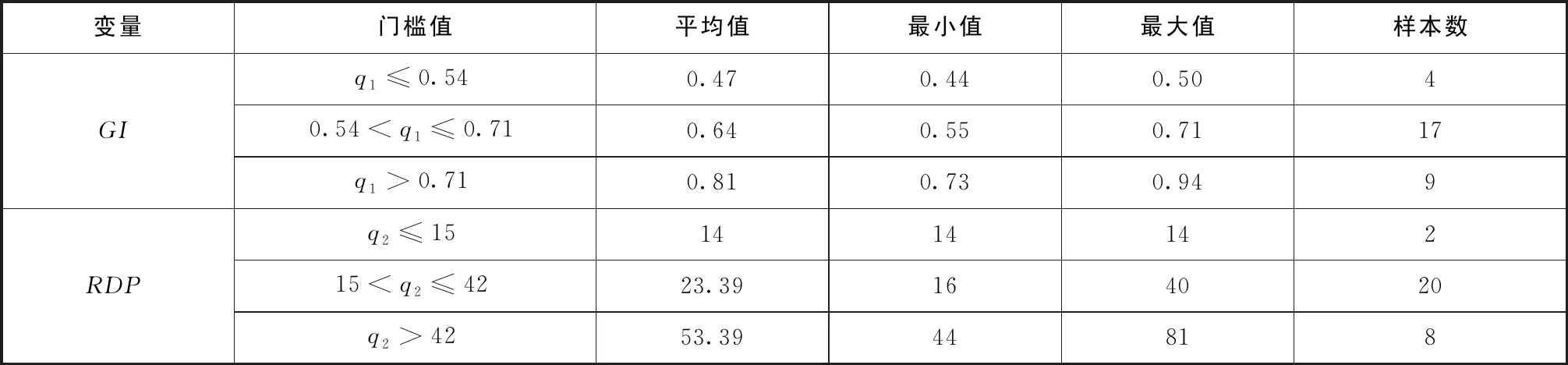
表7 2017年我国省际高校门槛变量的区间描述性统计

由表7可知，我国高校的政府科研投入强度处于最优区间的省份为17个，占比57%；处于第三区间的省份为9个，占比30%，其余省份处于第一区间。可以看出，整体上我国省份多数处于政府科研投入强度的合理区间；部分省份政府投入强度过大，这些省份或是由于政府科技投入存在冗余，或是由于来源于企事业单位的合作经费过少，科研经费结构不优。人均政府科技经费处于最优区间的省份为8个，占比27%；处于第二区间的省份为20个，占比67%，其余省份处于第一区间。可以看出，整体上我国省份多数处于研发规模对基础研究促进作用不显著的状态，需要进一步提高人均科技经费或控制人员规模，优化资源配置。

3.3 省际区间分布

各省份政府科技投入规模和强度的状态如图5所示。由图5可知，北京、上海和江苏这3个经济发达省份，处于政府投入强度的最优区间，同时政府科技经费投入较大的地区，因此基础研究产出效率较高。广东处于政府投入高强度的第三区间，存在一定投入冗余，但超过幅度不大。黑龙江、辽宁、重庆和四川等东部和西部四省，处于政府科技经费投入规模和强度的双低状态，科研资源稀缺对基础研究产生抑制作用；青海、宁夏、新疆、贵州、广西、海南、福建这7个主要位于西部欠发达地区的省份处于政府科技经费投入规模较低，但强度较高的状态，反映了这些省份科研经费来源渠道单一，与产业界的合作水平较低，这在一定程度上与区域经济发展水平相关。内蒙古、甘肃、云南、山西、河北、江西等省份处于政府科技经费投入对基础研究促进作用最优的区间，但经费投入规模偏低，可适当增加投入。

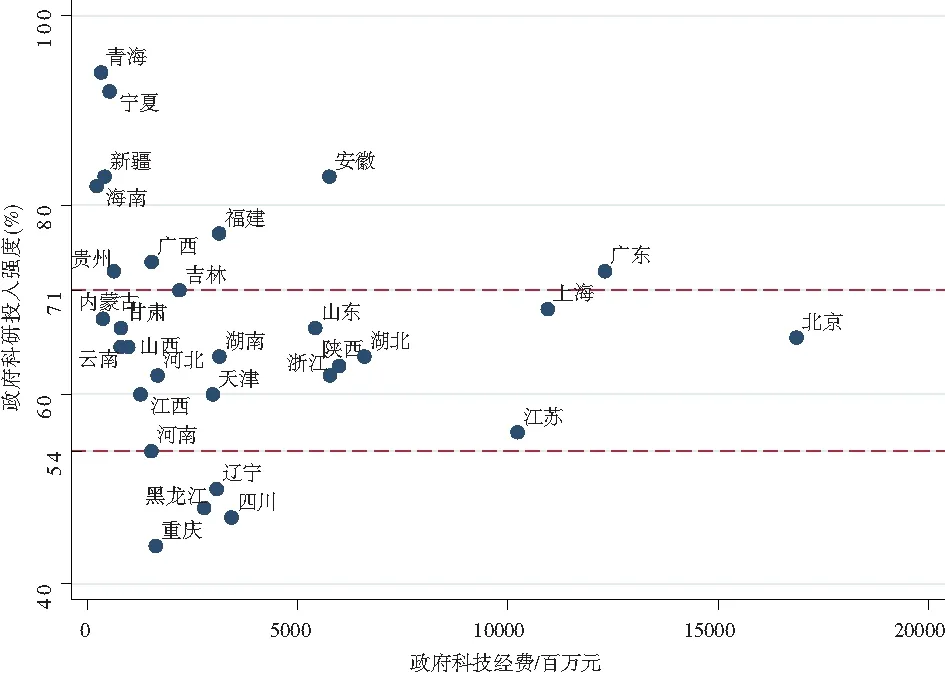
图5 政府科技经费投入规模和强度的区域分布

各省份研发人员规模和人均政府科技经费的状态，如图6所示。由图6可知，北京、上海、江苏和广东这4个经济发达省份处于研发人员规模和人均科研经费保障充足的最佳状态，研发人员对基础研究产出有较强的促进作用。青海人均政府科研经费较高，这主要是其研发人员规模偏低决定的。内蒙古和云南这两个西部省份处于研究人员规模和人均经费保障的双低状态，人员匮乏对基础研究产生消极影响；青海、宁夏、甘肃、贵州、新疆等西部欠发达地区研发人员规模偏低，人均政府投入科技经费也处于对基础研究促进作用不显著的第二区间，这与这些地区经济发展水平欠佳，对科研人员吸引力不强有关。

综合考虑政府科研投入强度和人均政府科技经费，其区域分布如图7所示。由图7可知，北京、上海、江苏、陕西和湖北这5个省份，政府科研投入强度和人均政府科技经费均处于最优区间，基础研究处于优势状态。重庆、四川、黑龙江和辽宁4个省份两个指标均处于偏低的非优区间，可适当增加政府科研投入。贵州、广西、福建、海南、新疆和宁夏6个省份处于人均政府科技经费不足，政府投入强度较高的状态，单纯依靠调整政府科技经费投入来优化两个指标存在一定悖论，无法同时满足最优区间，不能实现帕累托最优，此时应通过多元渠道改善资源配置状态，如可通过控制研发人员规模、增加高校其他渠道科研经费来源等。因此优化资源配置不能用同一种标准来衡量，需要综合考虑不同地区经济水平、发展状况、人员规模、经费来源和结构等方面。

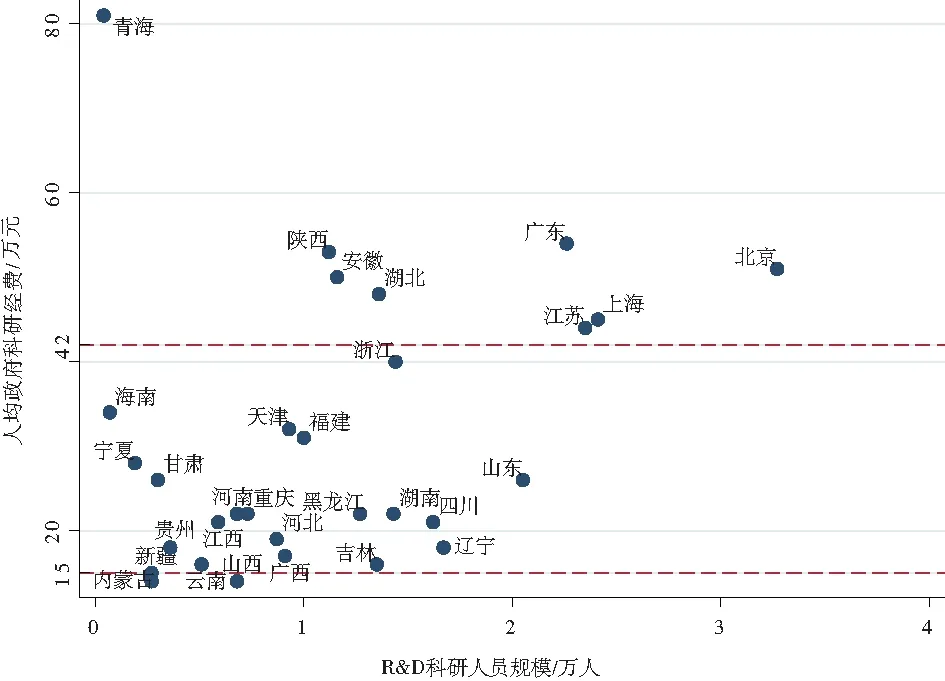
图6 研发人员规模和人均政府科技经费的区域分布

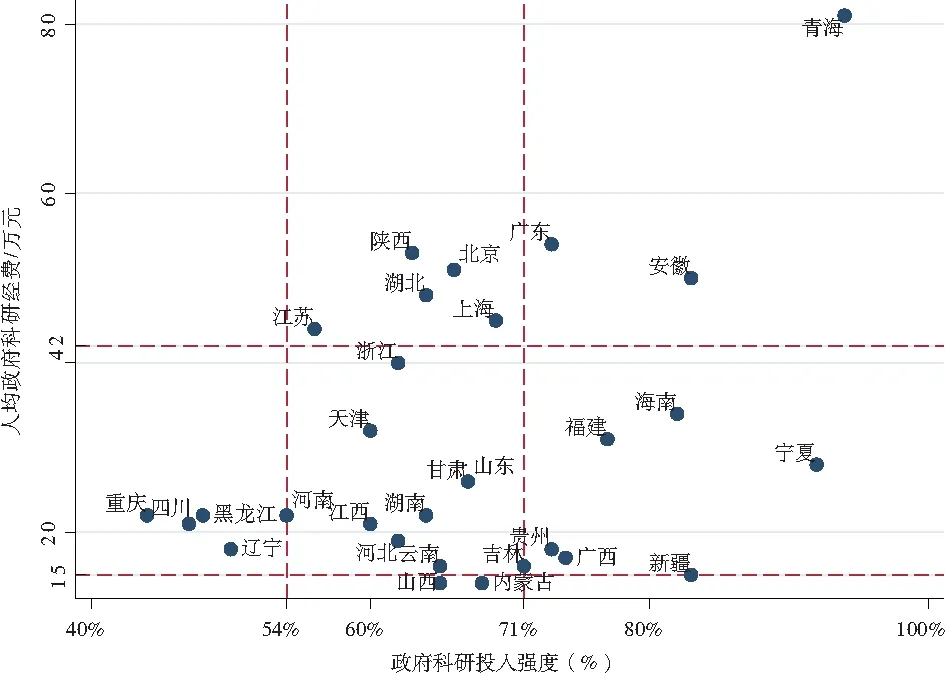
图7 政府科研投入强度和人均政府科技经费的区域分布

4 结论与启示

本研究选取2010—2017年我国30个省 (市、自治区)的面板数据，通过面板门槛模型实证分析政府科技经费投入和高校研发人员规模对于基础研究科研产出的影响。研究显示：基础研究投入产出效率受研发经费投入结构及人员经费匹配程度的影响和制约，因此综合考虑投入规模和资源配置结构就显得尤为重要。政府科技经费投入、研发人员规模和高校基础研究科研产出都存在非线性关系，政府投入强度适中时 (处于两个门槛值之间)是政府科技经费投入对基础研究产出的最优促进区间，政府科研投入强度过高 (高于第二门槛值)或过低 (低于第一门槛值)都会影响制约科研产出；在人均科技经费达到一定水平时 (高于第二门槛值)才能充分发挥研发人员规模对基础研究的促进作用，处于中等水平 (处于两个门槛值之间)促进关系会不显著，如果过低 (低于第一门槛值)则会负向影响基础研究产出。

我国整体上处于政府科研投入强度中等偏高、人均科技经费不足的情况，两个指标都呈现逐年递增的趋势。这反映了高校从企事业单位等途径获取的科研资源增长速度明显落后来自于政府科研投入的增长速度，高校对政府科研投入依赖性不断加强；各省 (市、自治区)科研资源和结构存在显著空间差异，相当一部分地区未处于最优水平。科研资源分布不均衡，与地区经济发展水平呈现出一定的相关性，东部经济发达地区科研资源较为丰富，来源渠道也较为多元；西部和中部欠发达地区则出现对政府依赖程度较大、政府投入相对有限的双重窘境。

本研究启示如下。

(1)高校科研要素 (人力资源、科研经费、设施设备、基地建设等)之间是相互联系、相互制约的复杂运行系统，要素之间协调匹配才能充分发挥各自功能和效益，政府科研投入和高校研发人员规模要考虑高校科研活动的承载能力。政府投入强度过低则直接作用于基础研究的资源有限；过高则会出现经费投入冗余和规模报酬递减现象，也会削弱高校产学研结合的动力和活力；人员规模过大则会出现人均科研资源不足的倾向。因此强调资源配置和优化结构比单纯追求规模的增加对基础研究活动更有意义。

(2)在保障政府科研投入强度一定水平的基础上，应注重优化高校科研经费来源结构，形成多元化经费投入体系。现实上，宏观政策层面上在短期内很难大幅增加对高校的科技经费拨款，微观层面上建立财政投入与社会资金搭配机制促进基础研究产出更具现实意义；理论上，适度的政府投入强度更能激发高校基础研究创新潜力。因此，应发挥政府的杠杆和导向作用，推动企事业单位参与高校科研活动，使高校通过产学研合作广泛吸纳和利用社会各方面的资金，优化科研经费配置结构。

(3)以全局视野统筹规划和调整我国省域高校科研资源。我国高校科研活动发展不均衡问题较为突出，政府科研投入的空间差距也较为明显。资源不足和投入冗余现象同时存在，需进一步协调优化省域间的科研资源和研发人员的配置和规模。此外，应加强高校间的资源共享和联动合作，加强高校间跨区域、跨类型的校际协同创新，打破资源分散、封闭和垄断的状况，提高研发人员协同效应和科研资源使用效益。

本研究存在以下不足：高校的科研产出分为许多形式，如代表应用研究的专利技术，代表成果转化的技术转让收入等，本研究在初步对产出几个指标做门槛效应分析后发现并不显著，为聚焦基础研究主题，并没有进一步讨论，在未来研究中将选择适合的计量方法进行专项分析。