Vortex Rossby Waves in Asymmetric Basic Flow of Typhoons
Tianju WANG,Zhong ZHONG∗,2,and Ju WANG
1College of Meteorology and Oceanography,National University of Defense Technology,Nanjing 211101,China
2Jiangsu Collaborative Innovation Center for Climate Change,Nanjing University,Nanjing 210023,China
1.Introduction
Observations have shown that when a tropical cyclone reaches a certain intensity,pronounced spiral cloud bands outside the eye wall of the tropical cyclone are formed(Huang and Chao,1980).Such spiral clouds are expected to grow along the radial direction and rotate around the typhoon center at a velocity not equal to the velocity of the basic flow(Liu and Yang,1980).Distinct wave-like fluctuations can be observed in the spiral cloud bands,indicating the existence of waves and eddies in the typhoon vortex(MacDonald,1968;Yu,2002).
Studies of wave structures in typhoons can be traced back to the 1940s,when it was found that the spiral cloud bands of typhoons exhibit many features similar to inertia-gravity waves in the shallow water model.These wave structures in typhoons could be well explained by gravity wave theory(Wexler,1947;Tepper,1958;Tatehira,1961).Huang and Chao(1980)indicated that the group velocity of inertiagravity waves in typhoons was about 90 km h−1,and Liu and Yang(1980)found that the average phase velocity of inertiagravity waves(C0)was 28 m s−1.Niu(1991)argued that inertia-gravity waves in an unstable condition is a key factor that determines the development of typhoons.Anthes(1972)and Kurihara(1976)simulated tropical cyclones and found that energy in typhoons is largely dissipated in the form of gravity waves.However,despite great progress in the study of typhoons with the theory of inertia-gravity waves,one critical weakness in the application of gravity wave theory for typhoon studies is that the theoretical propagation velocity of inertia-gravity waves is much faster than the observed moving speed of typhoon spiral cloud bands(Yu,2002).Thereby,it is necessary to seek other more reasonable explanations for the wave structures in typhoons.
As early as in the late 1960s,MacDonald(1968)found that wave structures similar to planetary Rossby waves exist in typhoons,which are actually the vortex Rossby waves proposed later by Montgomery and Kallenbach(1997).The theory of vortex Rossby waves overcomes the weakness of classical inertia-gravity wave theory,and yields a theoretical wave propagation velocity that is the same as in observations(Yu,2002).Shen et al.(2007)investigated vortex Rossby waves in both barotropic and baroclinic fluids,and their results indicated that barotropic and baroclinic vortex Rossby waves could be triggered by second-order horizontal and vertical shears in the basic flow of a typhoon.By studying the topographic impact on planetary Rossby waves,Luo and Chen(2003)investigated the influences of topography on the propagation of vortex Rossby waves using a quasi-geostrophic,barotropic model,and proposed the concept of topographic vortex Rossby waves.Deng et al.(2004)studied the effects of the Rossby parameter β in the formation of vortex Rossby waves using scale analysis and found that vortex Rossby waves could be triggered when the Rossby parameter β is introduced into a basic flow that even has no radial shears.Qiu et al.(2010)revealed a significant contribution of vortex Rossby waves to the formation of the secondary eye wall of a typhoon.In addition,based on their study of a typhoon process,Hall et al.(2013)indicated that the vortex Rossby waves with wavenumber-2 and 3 are closely linked with deep convection that develops rapidly in typhoons.Furthermore,wave ray theory has also been applied to study the impact of vortex Rossby waves on energy propagation in typhoons(Zhong et al.,2002).
Many previous studies have studied vortex Rossby waves from various perspectives.However,for simplicity,the basic flow of a typhoon is always assumed to be symmetrical;whereas,in reality,it is often asymmetrical.Due to the asymmetry in the basic flow of a typhoon,the vorticity gradient will change with azimuth angle,which could radically affect the nature of the vortex Rossby waves.Thereby,using an asymmetric typhoon basic flow that is more realistic will be helpful in improving vortex Rossby wave theory and obtaining more representative results.In the present study,based on wave ray theory,a model with an asymmetric typhoon basic flow is employed to discuss the group velocity of vortex Rossby waves and the nature of wave rays.
2.Vortex Rossby waves and rays in asymmetric basic flow of typhoons
Barotropic shallow water equations in the cylindrical coordinate system with thef-plane approximation can be written as(Liu and Liu,2011)

whereuis the radial velocity,vis the tangential velocity,ris the radius,θ is the azimuth angle(in radians),his the height of the free surface,f0is the Coriolis parameter,gis the gravitational acceleration,andtrepresents time.
The dimensionless variables listed below are introduced in the present study:

whereU0(∼ 101m s−1),R(∼ 106m),ΔH(∼ 102m)andT(∼105s)are the horizontal velocity,typhoon radius,temporal variability of height on the free surface,and characteristic time,respectively.Substituting the above variables for their corresponding variables in Eqs.(1)and(2),which are then divided by,we have
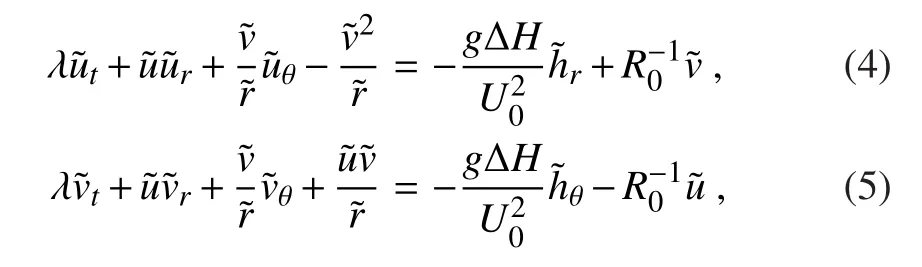

Assuming,both are constructed by basic flow and perturbation flow respectively,and substituting them foruandvin Eq.(6)yields
Without loss of generality,here,the tangential asymmetric basic flow is constructed by superimposing the wavenumber-1 perturbation flow on the symmetric tangential basic flow(Zhong et al.,2007).The dimensionless tangential asymmetric basic flow can be expressed by
With Eq.(8),the radial basic flow¯ucan be derived from the non-divergence equation as follows:

where µ (∼ 10−1)is the parameter of asymmetry for the basic flow,aandbare parameters for the basic flow structure,and θ0is the initial azimuth of the wavenumber-1 perturbation flow.When µ is set to zero,Eqs.(8)and(9)degenerate into an expression for the symmetric basic flow, and the larger value of µ corresponds to the stronger asymmetry in the basic flow.In addition,the radius of maximum wind(RMW)can be determined by parametersaandb.From Eq.(8),one can yield a value ofb−1/2for the RMW.In the present study,we seta=20 andb=100;then,the corresponding dimensionless RMW isr=0.1,which is about 100 km.Moreover,the locations of maximum and minimum velocities in the asymmetric basic flow are determined by the initial azimuth angle
Using the dimensional format of Eqs.(8)and(9)(Huang and Chao,1980)(i.e.,multiplied by the characteristic speedU0=50 m s−1)and specifying the initial azimuth angle θ0=0 and asymmetry intensity parameter µ =0.2,the distributions of the tangential symmetric basic flow,the tangential wavenumber-1 perturbation flow,the tangential asymmetric basic flow,and the radial basic flow,are shown in Figure 1.It is clear that the tangential asymmetric basic flow speed(Figure 1c)is no longer distributed as concentric circles symmetrical about the typhoon center due to the consideration of the tangential wavenumber-1 perturbation flow(Figure 1b).Instead,large values occur to the north of the typhoon center and the tangential basic flow speed is obviously not symmetric about the typhoon center.When µ=0.2,the maximum flow speeds in the tangential symmetric basic flow,the tangential wavenumber-1 perturbation flow and the tangential asymmetric basic flow are 50 m s−1,10 m s−1and 60 m s−1,respectively.Figure 2 shows the distributions ofandin Eq.(7),from which it can be seen thatis very small whenris relatively small,but it will increase quickly withr.So,in this study,we assume¯u(∂¯ζ/∂r)+(¯v/r)(∂¯ζ/∂θ)≈0 inr∼[0,0.35],as it is much smaller than the other items in this range.Moreover,the average tangential and radial speed within the ranges ofr∼ [0,0.35]and θ∼ [0,2π]in the asymmetric basic flow is 37.5 m s−1and −6.8 m s−1.
Based on the definition of the stream function(ψ),v=∂ψ/∂r,u=−(1/r)(∂ψ/∂θ),and the vorticity equation,Eq.(7),can be written in linear form inr∼[0,0.35]:

The solution to Eq.(10)can be obtained using the Wentzel-Kremers-Brillouin-Jeffreys(WKBJ)method.Suppose the solution to the slowly evolving wave packet(Zhong et al.,2002;Tao et al.,2012)is

where(R,T,Θ)= ε(r,t,θ)and ε is a parameter smaller than 1,we have
Fig.1.Distributions of the speed of tangential and radial basic flow(units:m s−1):(a)tangential symmetric basic flow;(b)tangential wavenumber-1 perturbation flow;(c)tangential asymmetric basic flow;(d)radial basic flow(the abscissa and ordinate indicate dimensionless distances from the typhoon center).
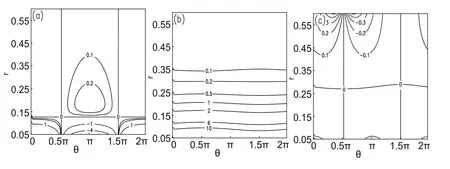
Fig.2.Distributions of(a)andon the θ–r plane.
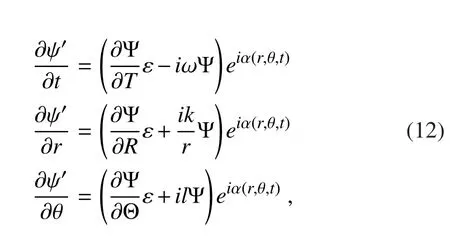
wherekandlare radial and tangential wavenumbers,respectively.Substituting Eq.(12)into Eq.(10)and omitting the small term that includes ε,we obtain the frequency equation for vortex Rossby waves:

which yields

where ω is the frequency.
The radial and tangential group velocities,Cg,randCg,θLiu and Yang(1980),can be expressed as
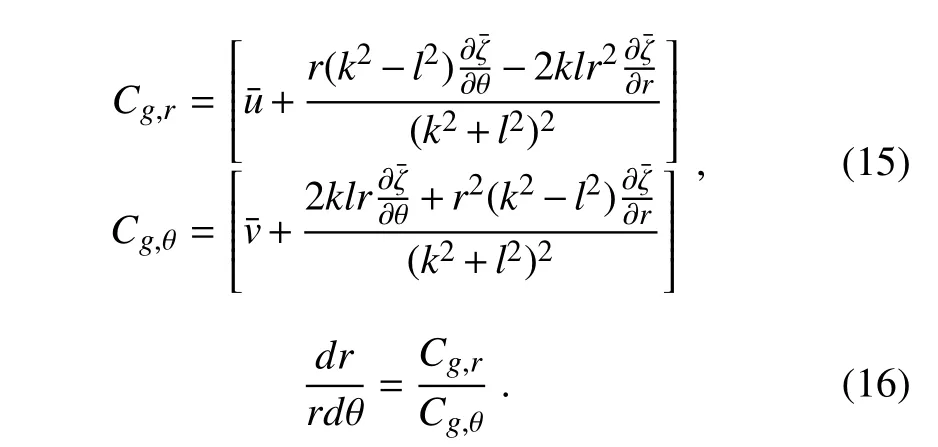
Substituting Eq.(15)into Eq.(16),we can obtain Eq.(17)shown below:

wheredr/(rdθ)is the slope of the wave ray.
Integration of Eq.(17)can yield the rays of vortex Rossby waves in asymmetric basic flow.
3.Numerical solution of the wave ray equation
Since it is hard to obtain the analytical solution of the wave ray,Eq.(17),here,we seek its solution by numerical integration.The scheme for numerical integration is written as

wherenis the number of integration steps,Δθ is the integration step,andf(r,θ)is the term on the right-hand side of Eq.(17).The initial value θ(0)is set to zero;the integration range ofris set to[0,0.35];the integration step Δθ=0.01;and wavenumberk=l=1.Figure 3 presents the wave rays obtained by numerical integration under the above conditions when µ is set to 0,0.2 and 0.3,respectively.

Fig.3.Wave rays corresponding to various values of µ(the abscissa and the ordinate indicate dimensionless distances from the typhoon center).
Figure 3 shows that the vortex Rossby wave rays propagate outward in a spiral pattern.The distances from the typhoon center of the wave rays increase with the azimuth angle and,apparently,the differences between the rays increase with the intensity of asymmetry(µ).The larger the value of µ,the greater the increase in the distance of the wave ray,and that makes a wave ray with larger µ farther away from the typhoon center.Although the difference between the asymmetric wave ray and the symmetric one is still large,the difference between wave rays for µ =0.2 and µ =0.3 becomes smaller with the increasing ofr.This suggests that the impact of the basic flow asymmetry on wave rays will generally decrease and ultimately be constrained within a certain radius.
4.Group velocity
Based on Eq.(17)for wave rays,the radial and tangential group velocities(Cg,randCg,θ)are two important factors affecting wave rays.In the following,we take µ =0.2 and θ0=0 as an example to explore the impacts of asymmetric basic flow on the vortex Rossby wave rays via analyzing characteristics of the radial and tangential group velocities.
Figure 4 displays the distributions of dimensionless radial group velocityCg,ron the θ–rplane in both symmetric and asymmetric basic flows.In the symmetric basic flow(Fig.4a),Cg,ris always irrelevant to azimuth angle θ and only changes with radiusr.The large value ofCg,rappears atr=0.1(where the maximum tangential wind speed appears).In the asymmetric basic flow(Fig.4b),Cg,rchanges with bothrand θ and the largest value also appears at aroundr=0.1.The average dimensionless value ofCg,ris about 0.50 and the largest is 1.21 within the ranges ofr∼[0,0.35]and θ∼[0,2π],corresponding to an average and maximum radial group velocity of 25 m s−1and 60.5 m s−1.With Eq.(8),it can be found that when µ=0.2 the dimensionless maximum radial basic flow velocity¯uis−0.16,corresponding to−8.0 m s−1,which is much slower than the maximumCg,r.The average dimensionless radial basic flow speed is−0.14,corresponding to the average value of−6.8 m s−1,which is also much slower than the averageCg,r.When compared with¯v,although the averageCg,ris smaller,the maximum value ofCg,ris almost the same as¯v.This indicates that the characteristic ofCg,ris identical to that of¯v,and the wave energy could propagate outward rapidly.
(2)当AFA 1和AFA 2的掺量分别为2.5‰和3.0‰时,UHPC的28 d抗压强度分别提高28.5%和21.5%;当AFA 1和AFA 2的掺量分别为3.5‰和3.0‰时,UHPC的28 d抗折强度分别提高了30.2%和28.8%。
The difference between radial group velocities in symmetric and asymmetric basic flows can be written as
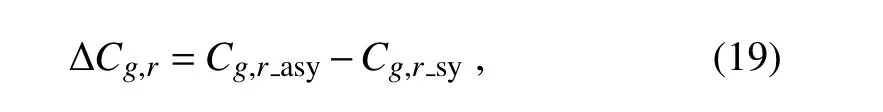
whereandare radial group velocities in symmetric and asymmetric conditions,respectively.
The distribution of ΔCg,ron the θ–rplane is displayed in Fig.5,which shows that ΔCg,ralso reaches its maximum at aroundr=0.1.
It is worth noting that the distributions ofCg,rand ΔCg,rshown in Fig.4 and Fig.5 are obtained under the condition of an initial azimuth angle θ0=0 in the tangential wavenumber-1 perturbation flow and the radial basic flow.Compared with Fig.1,it is easy to identify that ΔCg,ris affected by both the features of asymmetry in the tangential and radial basic flows.For example,the maximum and minimum values of the wavenumber-1 perturbation flow are located at azimuth angles of θ=0.5π and 1.5π,and the locations of maximum and minimum values of the radial basic flow are at a θ= π and 0.Whenris small,the maximum and minimum values of ΔCg,rappear at θ≈ π and 2π,which is close to the location of the maximum and minimum values of¯u.Whereas,for the largerr,the location of the maximum and minimum values of ΔCg,rwill rotate clockwise and approach those of¯v,as shown in Fig.5.This suggests that both the tangential asymmetric wavenumber-1 flow and the radial basic flow can affect the distribution of radial group velocityCg,r;however,the tangential and radial basic flow shows different importance for differentr.Generally,the locations of the maximum and minimum value of ΔCg,rare closely linked with the azimuth angles of the asymmetry.Therefore,if the asymmetries of the basic flows intensify at specific azimuth angles,thenCg,rwill increase around these angles,and the wave energy will propagate outward more rapidly there.Similarly,when the asymmetry decreases at specific azimuth angles,the wave energy will propagate outward more slowly along these directions.
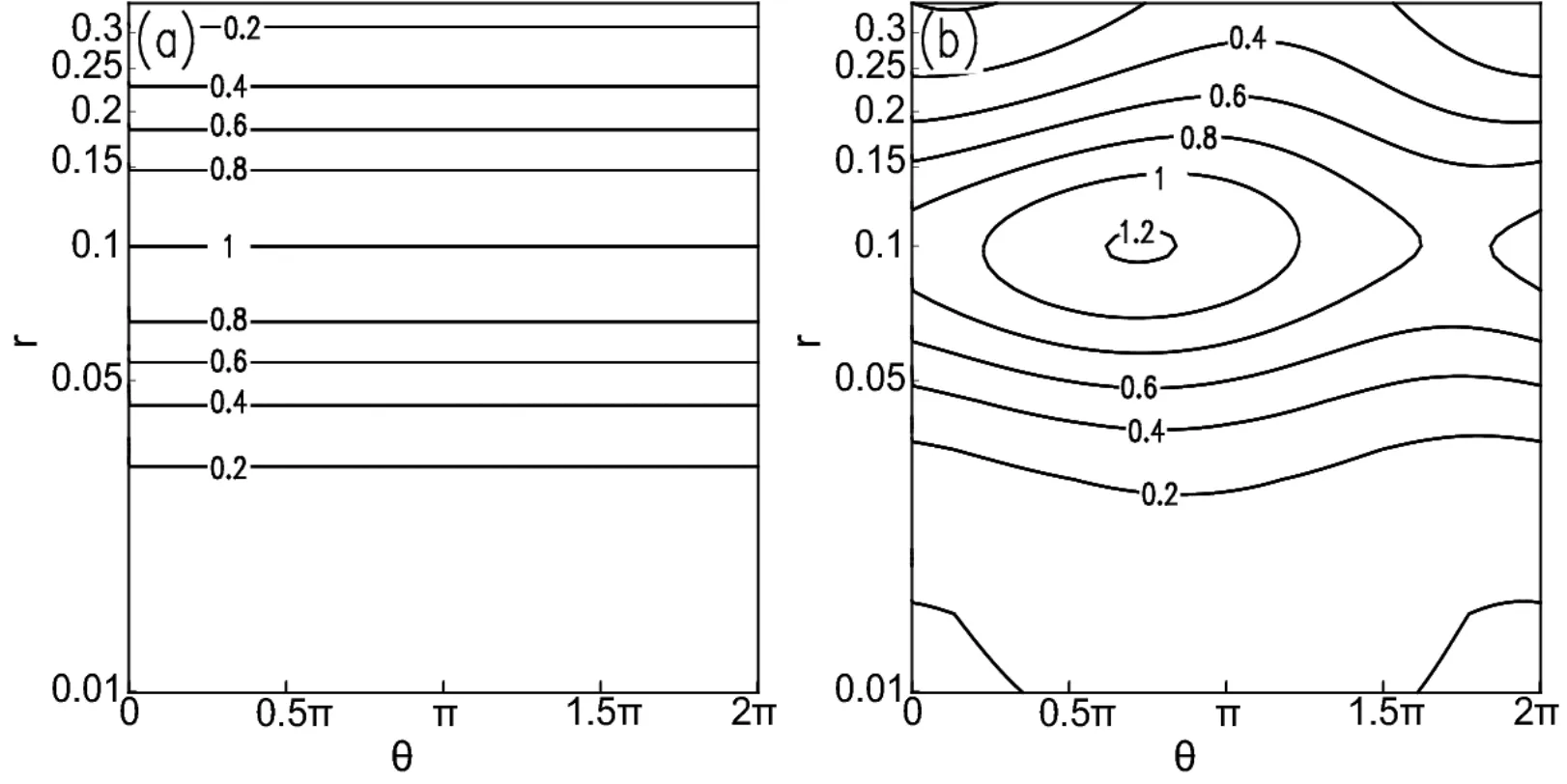
Fig.4.Distributions of dimensionless radial group velocity Cg,ron the θ–r plane in(a)symmetric basic flow and(b)asymmetric basic flow.
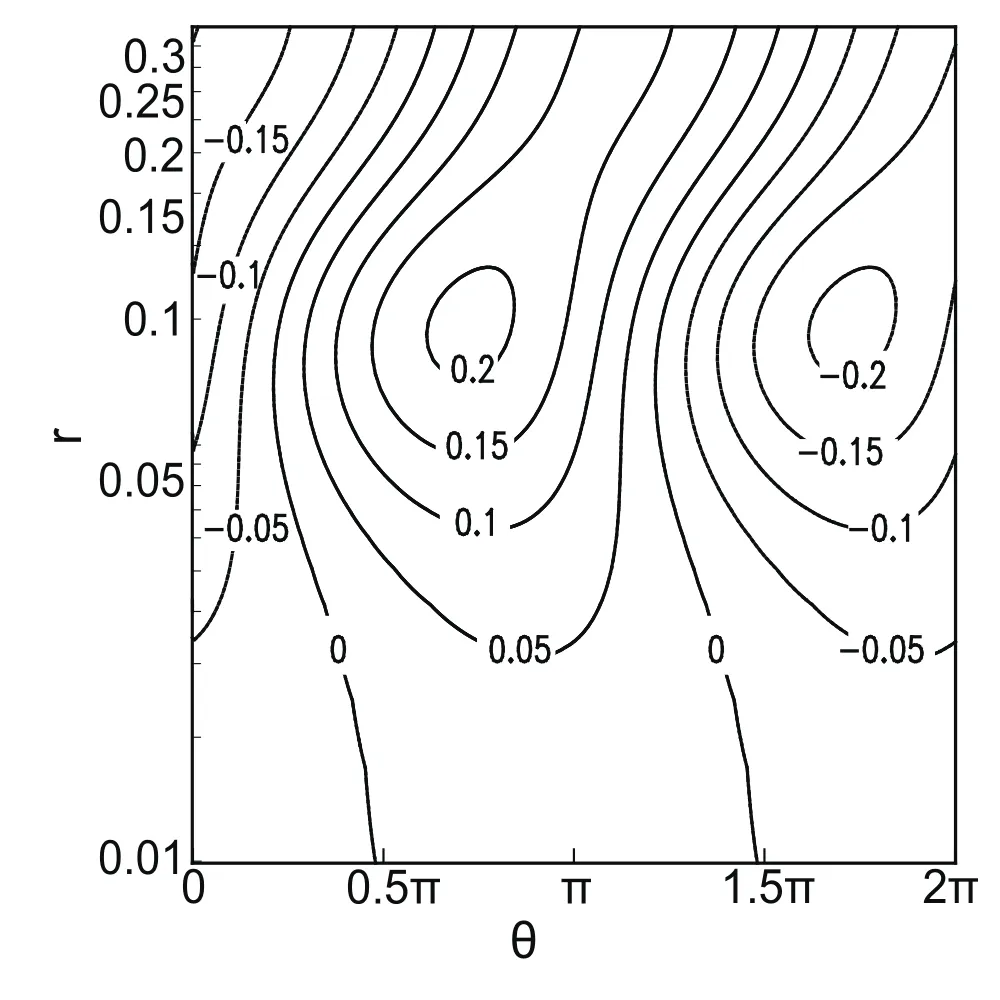
Fig.5.Distribution of ΔCgron the θ–r plane.
The distribution of tangential group velocityCg,θon the θ–rplane is presented in Fig.6,which shows that the distribution ofCg,θ(Fig.6a)in the symmetric basic flow is similar to that ofCg,r(Figure 4a),and both change only with radius and reach their maximum values atr=0.1.In the asymmetric basic flow,however,although the maximum values ofCg,randCg,θboth appear at aroundr=0.1(Fig.6b and Fig.4b),with little difference in values,Cg,θis much larger thanCg,rat a certain radius(e.g.,atr=0.3,Cg,r≈ 0.2,Cg,θ≈ 0.6),indicating thatCg,randCg,θare different from each other.Cg,rdecreases more rapidly along the radial direction,and thereby the speed of wave energy propagation along the radial direction will become slow beyond a certain radius.In contrast,the radial gradient ofCg,θis relatively small,so the tangential propagation of wave energy can still maintain in regions far away from the typhoon center.It can be estimated that the average value of dimensionlessCg,θin the region shown in Fig.6(r∼ [0,0.35],θ∼ [0,2π])is 0.75,which corresponds to 37.5 m s−1,and is just the same as the average value of¯v.Whereas,the maximum value of dimensionlessCg,θis 1.20,corresponding to 60.0 m s−1,which is also the same as the maximum value of¯v.This suggests that wave energy can propagate along the tangential direction at the average speed of the tangential basic flow.In short,the wave energy propagation along the tangential direction is much faster than that in the radial direction.
The difference between tangential group velocities in symmetric and asymmetric basic flows(ΔCg,θ)can be expressed as
whereandare the tangential group velocities in symmetric and asymmetric basic flows,respectively.
Figure 7 shows the distribution of ΔCg,θon the θ–rplane.ΔCg,θchanges with both azimuth angle θ and radiusr.The change in ΔCg,θwith θ demonstrates the asymmetric feature of tangential wavenumber-1 flow and the radial basic flow,and the azimuth angles corresponding to the locations of asymmetric maximum and minimum values also change withr.
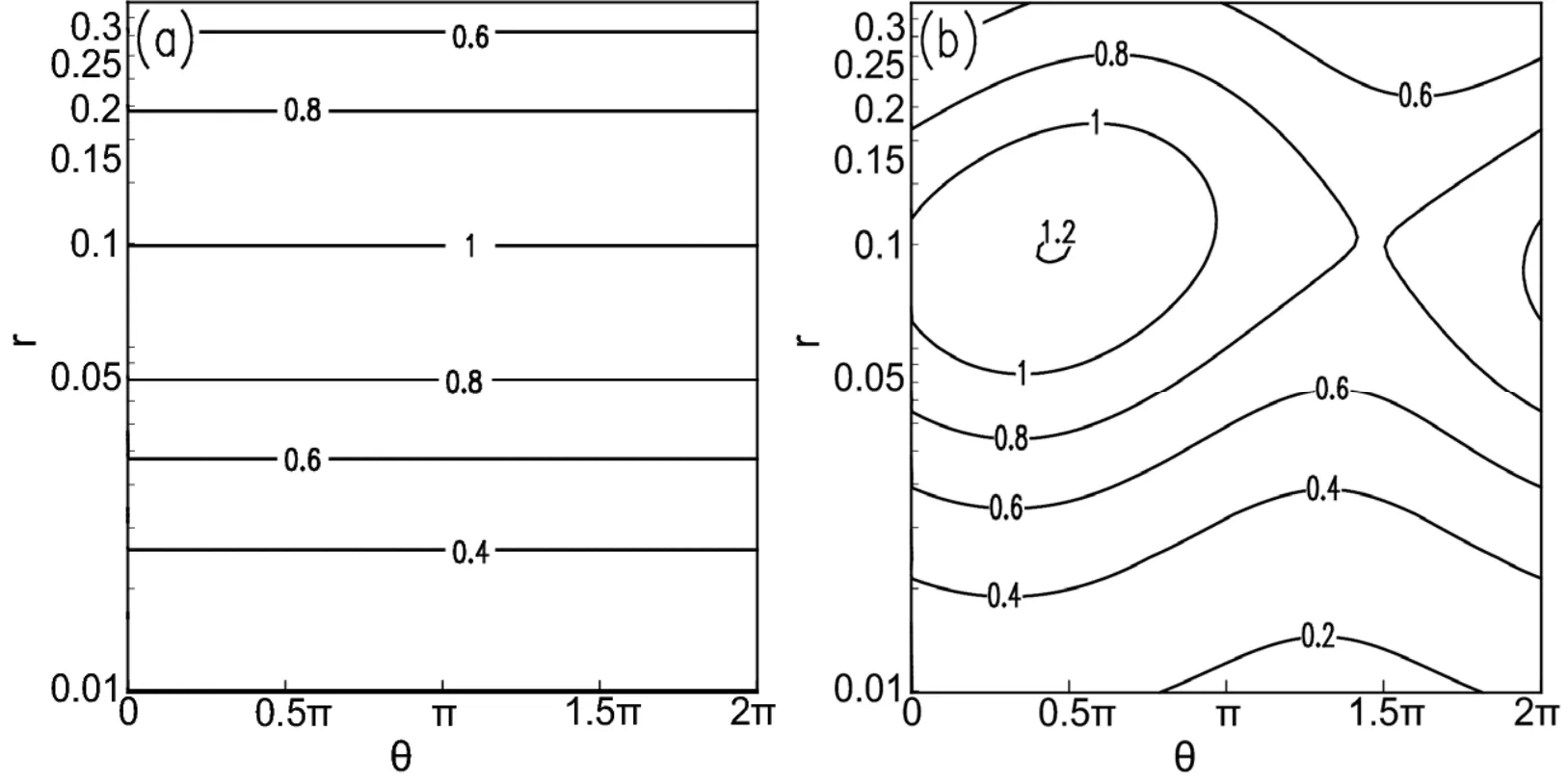
Fig.6.Distribution of dimensionless tangential group velocityCg,θon the θ–r plane in(aθ)symmetric basic flow and(b)asymmetric basic flow.

Fig.7.Distribution of ΔCg,θon the θ–r plane.
Compared with Fig.1,it is clear that whenris relatively small,the large and small values of ΔCg,θare located just between the locations of the maximum and minimum value of¯vand¯u(e.g.,whenr∼[0.01,0.05],the maximum and minimum values of ΔCg,θare located at about 0.3π and 1.3π),which means that the basic flow¯vand¯uare both important at this radial scope.However,whenrbecomes larger,areas of large and small values of ΔCg,θturn anticlockwise and basically overlap areas of large and small values of wavenumber-1 perturbation flow(e.g.,whenr≈0.1,the large and small ΔCg,θare located at about 0.5π and 1.5π),which suggests that the tangential wavenumber-1 perturbation plays a more important role for such conditions.Moreover,the locations of large and small ΔCg,θturn anticlockwise with a continuous increase ofr,indicating that the influence of radial flow decreases rapidly with increasingr.As a result,both the tangential wavenumber-1 perturbation flow and the radial basic flow both can increase(decrease)the value of ΔCg,θ,but the importance of the radial basic flow is only concentrated in areas for smallerr,and ΔCg,θis dominated by the tangential wavenumber-1 perturbation whenrbecomes larger.
Based on the wave ray equation,Eq.(17),the ratio ofCg,rtoCg,θdetermines the ray slope of vortex Rossby waves.Distributions of ray slopes in symmetric and asymmetric basic flows are shown in Fig.8,which indicates that in the symmetric basic flow(Fig.8a)the ray slope is only associated with the radius,and its distribution is similar to that of the group velocity,with the maximum value occurring atr=0.1.In the asymmetric basic flow(Fig.8b),the distribution of the ray slope is completely different to that of the group velocity,although the large ray slope still occurs at aroundr=0.1.Impacts of asymmetry in the basic flow on the wave ray slope are mainly concentrated near the RMW,and the azimuth angle corresponding to the maximum wave ray slope is at around θ=1.13π.Differences between the ray slopes in symmetric and asymmetric basic flows(Fig.9)indicate that large differences also occur around the RMW, whereas the azimuth angle corresponding to the largest difference varies with the maximum speed of tangential wavenumber-1 perturbation flow and the radial basic flow.It is worth noting that the influence of asymmetry is still important for largerr,and this can explain the reason why the difference between wave rays of asymmetric flow and symmetric flow is great in Fig.3.
5.Conclusions
In the present study,wave ray theory is applied to investigate the impact of asymmetry in basic flow of typhoons on vortex Rossby waves,including the wave ray path,the group velocity,and the wave ray slope.The major conclusions are as follows:

Fig.8.Distribution of the wave ray slope on the θ–r plane in(a)symmetric and(b)asymmetric basic flow.

Fig.9.Differences between wave ray slopes in asymmetric and symmetric basic flows on the θ–r plane.
(1)Compared to symmetric basic flow,the asymmetry in the basic flow will change the ray paths of vortex Rossby waves in typhoons.The wave rays of the asymmetric basic flow are always located outside that of the symmetric basic flow.Stronger asymmetry in the basic flow corresponds to a larger difference between the wave rays in symmetric and asymmetric basic flows.The impacts of the asymmetry in the basic flow on the wave ray path are mainly concentrated in areas for smallerr,and it will diminish generally with increasingrbeyond a certain radius.
(2)The asymmetry in the basic flow has substantial impacts on radial and tangential group velocities of vortex Rossby waves.In the asymmetric basic flow,the radial and tangential group velocities change not only with the radius,but also the azimuth angle.The impact of asymmetry in the basic flow on group velocity is mainly concentrated near the RMW.Maximum wave energy propagation speeds along the radial and tangential directions near the RMW are almost equivalent to the maximum speed of tangential basic flow.Both the tangential basic flow and the radial basic flow can affect the group velocities,but the influence of radial basic flow only appears for smallerr,whereas the influence of tangential basic flow can maintain in the whole area we studied.
(3)The asymmetry in the basic flow can change the wave ray slope by affecting the radial and tangential group velocities of vortex Rossby waves,and eventually influence the wave ray path.However,the impact of asymmetry in the basic flow on the wave ray slope is mainly concentrated near the RMW.
Note that the above results are based on vortex Rossby waves on thef-plane;the β-plane and the three-dimensional structure of vortex Rossby waves in asymmetric conditions should be considered in the future.
Acknowledgements.This work was sponsored by the National Natural Science Foundation of China(Grant No.41430426).
Anthes,R.A.,1972:Development of asymmetries in a three dimensional numerical model of the tropical cyclone.Mon.Wea.Rev.,100,461–476,https://doi.org/10.1175/1520-0493(1972)100<0461:DOAIAT>2.3.CO;2.
Deng,L.T.,S.K.Liu,X.D.Xu,and Z.T.Fu,2004:The effect of Rossby parameter in vortex Rossby wave.Journal of Tropical Meteorology,20(5),483–492,https://doi.org/10.3969/j.issn.1004-4965.2004.05.004.(in Chinese with English abstract)
Hall,J.D.,M.Xue,L.K.Ran,and L.M.Leslie,2013:High-resolution modeling of typhoon Morakot(2009):vortex Rossby waves and their role in extreme precipitation over Taiwan.J.Atmos.Sci.,70(1),163–186,https://doi.org/10.1175/JAS-D-11-0338.1.
Huang,R.X.,and J.P.Chao,1980:The linear theory of spiral cloud bands of typhoon.Scientia Atmospherica Sinica,4(2),148–158,https://doi.org/10.3878/j.issn.1006-9895.1980.02.06.(in Chinese with English abstract)
Kurihara,Y.,1976:On the development of spiral bands in a tropical cyclone.J.Atmos.Sci.,33,940–958,https://doi.org/10.1175/1520-0469(1976)033<0940:OTDOSB>2.0.CO;2.
Liu,S.K.,and D.S.Yang,1980:The spiral structure of the tropical cyclone.Acta Meteorologica Sinica,38(3),193–204,https://doi.org/10.11676/qxxb1980.024.(in Chinese with English abstract)
Liu,S.K.,and S.D.Liu,2011:Basic equations of atmospheric motions.Atmospheric Dynamics,2nd ed.,S.K.Liu and S.D.Liu,Eds.,Peking University Press,Beijing,39–40.(in Chinese)
Luo,Z.X.,and L.S.Chen,2003:The influence of topography on vortex Rossby waves.Progress in Natural Science,13(4),372–377,https://doi.org/10.3321/j.issn:1002-008X.2003.04.007.(in Chinese)
MacDonald,N.J.,1968:The evidence for the existence of Rossbylike waves in the hurricane vortex.Tellus,20,138–150,https://doi.org/10.1111/j.2153-3490.1968.tb00358.x.
Montgomery,M.T.,and R.J.Kallenbach,1997:A theory for vortex Rossby-waves and its application to spiral bands and intensity changes in hurricanes.J.Roy.Meteor.Soc.,123,435–465,https://doi.org/10.1002/qj.49712353810.
Niu,X.X.,1991:The effect of inertial gravity waves on the occurrence,development and movement of typhoon in unsteady state.Acta Oceanologica Sinica,13(3),325–332.(in Chinese)
Qiu,X.,Z.-M.Tan,and Q.N.Xiao,2010:The roles of vortex Rossby waves in hurricane secondary eyewall formation.Mon.Wea.Rev.,138,2092–2109,https://doi.org/10.1175/2010MWR3161.1.
Shen,X.Y.,J.Ming,and K.Fang,2007:The properties of wave in typhoon and its numerical simulation.Scientia Meteorologica Sinica,27(2),176–186,https://doi.org/10.3969/j.issn.1009-0827.2007.02.009.(in Chinese with English abstract)
Tao,J.J.,X.H.Hu,and C.K.Li,2012:The formation mechanism and change characteristics of the wavenumer-1 vortex Rossby wave in the typhoon.Acta Meteorological Sinica,70(6),1200–1206,https://doi.org/10.11676/qxxb2012.101.(in Chinese with English abstract)
Tatehira,R.,1961:Analysis of small precipitation areas and bands,case study of typhoon “Hellen”.Second Technology Conference of Hurricanes,Miami,FL,American Meteorology Society,115–126.
Tepper,M.A.,1958:A theoretical model for hurricane radar bands.Preprints of 7th Weather Radar Conference,Miami,FL,American Meteorology Society,56–65.
Wexler,H.,1947:Structure of hurricanes as determined by radar.Annals of the New York Academy of Sciences,48(8),821–845,https://doi.org/10.1111/j.1749-6632.1947.tb38495.x.
Yu,Z.H.,2002:The spiral rain bands of tropical cyclone and vortex Rossby waves.Acta Meteorologica Sinica,60(4),502–507, https://doi.org/10.3321/j.issn:0577-6619.2002.04.014.(in Chinese with English abstract)
Zhong,K.,J.W.Kang,and Q.P.Yu,2002:Vortex Rossby waves in hurricane.Acta Meteorologica Sinica,60(4),436–441, https://doi.org/10.3321/j.issn:0577-6619.2002.04.006.(in Chinese with English abstract)
Zhong,Z,X.-T.Wang,and J.-S.Zhang,2007:The possible mechanism on the formation and intensification of the maximum wind core in tropical cyclone.Asia-Pacific Journal of Atmospheric Sciences,43,101–110.
 Advances in Atmospheric Sciences2018年5期
Advances in Atmospheric Sciences2018年5期
- Advances in Atmospheric Sciences的其它文章
- Analysis of the Characteristics of Inertia-Gravity Waves during an Orographic Precipitation Event
- Geometric Characteristics of Tropical Cyclone Eyes before Landfall in South China Based on Ground-Based Radar Observations
- Characteristics and Preliminary Causes of Tropical Cyclone Extreme Rainfall Events over Hainan Island
- Numerical Study of the Influences of a Monsoon Gyre on Intensity Changes of Typhoon Chan-Hom(2015)
- The 30–60-day Intraseasonal Variability of Sea Surface Temperature in the South China Sea during May–September
- Organizational Modes of Severe Wind-producing Convective Systems over North China
