收入动因成本性态分解模型有效性实证研究

董笑怡 吉林财经大学

引言

近年来，对于成本的分类和计算经历着巨大变革。传统的、完全财务会计性质的成本计算已不能适应现代企业的经济情况。在现实的经济生活中，完全固定成本或完全变动成本是非常极端的状况，比较少见。大多数的成本是处于两者之间的混合状态，因此合理有效的成本性态分解模型是非常值得研究的。

成本性态的方法计算成本强调成本总额依据业务总量而变化，例如，产量或销售量，此时变动成本=单位变动成本×业务量。该汽车公司的产量和销量都比较明显，作为本文实证分析的研究对象之一。然而，有越来越多行业的业务总量已经变得越来越模糊，根据成本习性计算成本，由于业务量不明确，管理会计所能发挥出来的作用也被弱化。

传媒行业是一个业务量非常模糊的行业。随着互联网的发展，传媒行业带来的附加值不断升高，竞争越来越激烈。努力调整产业结构，优化企业价值链，降低成本，是管理者必须要做的。因此，对成本和收入的预测、管理就显得尤为重要。

一、收入动因成本习性分解模型的提出

当企业的业务量不能明显地被捕捉到时，研究者必然会寻找另外的动因来代替业务量。该动因应该不仅是所有企业共有的、明显的并且容易获得的，更应该展示出它与成本之间紧密的联系。马元驹、杨琳在2016 年提出一个新的动因——营业净收入。用营业净收入替代产销量作为新的成本动因，计算出变动成本。得出下面的运算公式：

收入成本动因=固定成本+变动成本=固定成本+变动成本率×营业净收入。

在两位学者提出新动因的基础上，本文对动因做一次线性回归模型提供的预测方程，发现一次回归分析常数项不够显著，不能对系统的数据进行合理有效的分析。除此之外，一次线性回归模型常数项有可能出现负数，在现实生活中，固定成本几乎不可能为负数，该模型往往与经济实质不相符。为了解决问题，在一次线性回归模型的基础上进一步研究二次函数回归模型，展示出二次函数回归分析的优越性。

二、构建模型解决问题

（一）问题的提出

一次函数回归分析模型中的常数项不显著，或常数项为负。

研究案例：以某汽车公司为例，结果常数项不显著。

根据新浪财经网中该汽车公司2019-2020 年的季度、半年以及年度财务报表，经过简单计算得出的研究数据；数据包括2019 年四个季度和2020 年前三个季度的成本费用、营业净收入。

构建一次函数的模型为Y=a+bX，自变量和因变量具体含义如表1，这里指的营业收入不是指财务报表上的营业总收入，而是扣除了营业税金及附加的部分，在构建模型时，从经济实质的角度上来看，认为企业这营业税金及附加这部分没有真正的控制权。而收入成本动因也不简单的指营业成本，在企业运营中，管理部门、销售部门以及财务部门为支持部门，这些部门虽不是生产产品的部门，但是这些部门对于生产产品以及公司几乎全部的经营活动都是必不可少的，所以收入成本动因也包括了由这些部门产生的相关费用。

经过计算分析后可以得出直线的表达式为Y=1832476379+ 0.8675849932*X，使用该一次模型R2=0.95415，显然一次回归分析模型拟合优度较好，X 显著，但是常数项Prob=0.2852，这远超过既定的0.05 的范围，常数项不显著。一次函数回归分析模型并不理想。

研究案例：传媒行业，常数项不显著且小于0。

本文又选取了五大传媒企业（以下代称A、B、C、D、E），根据2019 年的年度财务报表，摘选出成本、费用（收入动因）以及营业净收入等相关数据，搜集数据来自新浪财经网，构建Y=a+bX（自变量与因变量的具体含义如表1 所示）。

经过计算分析后可以得出一次函数模型为Y=-107147089.3+ 0.8233284994*X，该一次函数模型R2=0.9585，R2趋近于1，拟合优度较好，X 显著，但是常数项Prob=0.9021，这远超过设定的0.05 的范围，常数项不显著且常数项为负。一次函数回归分析的有效性、适用性较差。

表1 自变量与因变量的具体含义

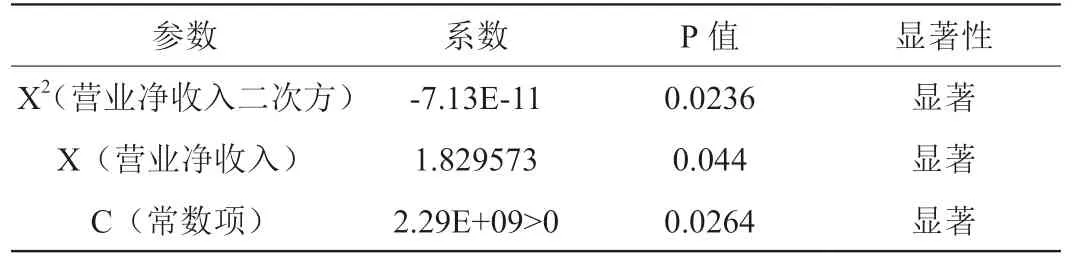
表2 传媒行五家公司二次回归模型分析数据

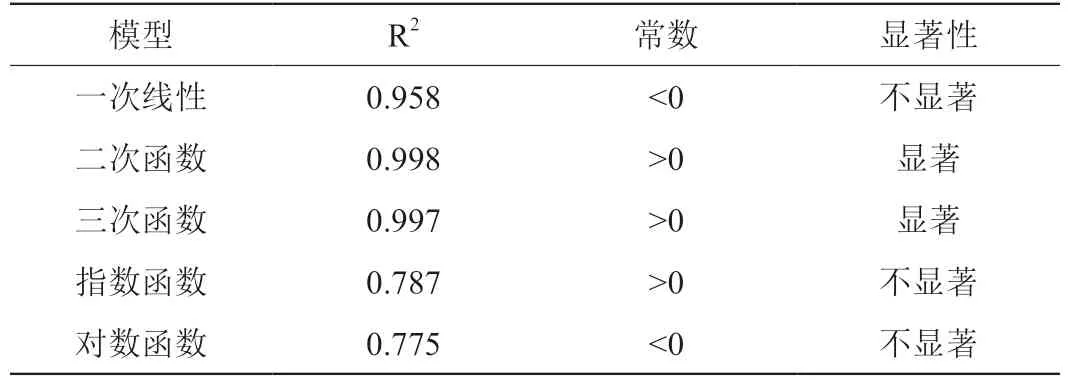
表3 传媒行五家公司收入成本动因模型汇总

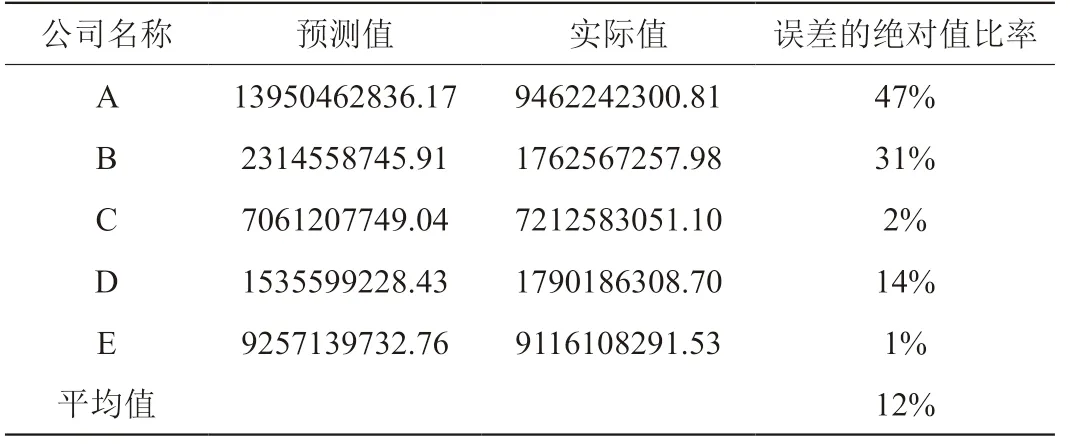
表4 传媒行业5家公司根据收入成本动因计算出成本的预测值与真实值得对比

（二）解决问题

为了解决一次回归线性分析中常数项不显著以及常数项为负的问题，对二次线性回归方程展开了分析，按照上述的传媒行业为研究对象，计算出二次函数的回归分析常数项显著且避免为负的结果，表明可以用二次函数分解模型代替一次函数分解模型。

按照财务报表中的数据，传媒行业的五大公司的收入成本动因二次函数的回归分析如表2 所示。

二次函数模型为Y=2 2 8 7 6 4 0 5 4 4+1.8 2 9 5 7 2 8 0 7*X- （7.134215112E-11）*X2，R2=0.998，由此可见，二次函数回归分析常数项显著，常数项大于0，且二次函数的R2大于一次函数的R2，这说明二次函数的拟合优度要比一次函数好。

除此之外，针对传媒行业，简单探讨了另外几种模型，例如，三次函数，指数函数，对数函数。最终发现二次函数的拟合优度最高，常数项显著，且为正数，可以推理出二次函数分解模型是更为理想的模型。表3 简单列出了另外几种模型的相关分析。

（三）问题的验证

为了进一步验证二次函数模型拟合的准确性，根据已有的二次函数模型，预测了五家传媒公司的2019 年度的成本，并与实际情况对比，如表4 所示。

表4 中计算出的误差比率=（预测值-实际值）/实际值，将误差比率算术平均后，可以得到平均误差比率为12%，因此可以推理出二次函数的回归分析较为准确，为较理想的模型。

为了更好地管理成本，管理者完全可以根据二次函数回归分析的模型，预测成本。将预测的成本与实际成本加以对比，寻找差异之处，调查成本差异的原因。找到问题后及时解决，提高公司整体运营的效率，提高利润。与此同时，可以对公司在行业当中的竞争对手进行分析，进行横向对比，这样既可以了解对手的运营情况，又可以向竞争对手学习，不断优化、提高自己，以求得在市场上获得更高的竞争力。

结语

随着越来越多的行业业务量增加，单一的使用单位变动成本×业务量已经不能满足企业成本核算的需求，构建成本性态分解模型无疑是好的选择。本文选取产销量较为确定的汽车公司以及业务量比较模糊的传媒行业作为实证研究对象，构建一次回归方程的，发现一次回归方程可能出现常数项不显著以及常数项为负的问题，为了解决问题，继续研究二次回归方程，二次分解模型的拟合优度比一次更高，且避免了常数项不显著以及常数项为负的问题，展示出了二次回归模型的优越性。

在现实经济生活中，准确地找到并核算出成本动因往往是非常困难的，利用财务报表中的营业净收入为成本动因，不仅提高了准确性，还大大降低了企业为寻找成本动因所付出的成本。与此同时，也可以通过查看其他公司的财务报表中的数据，进行回归分析，作为横向对比。

本文研究仍待改进之处：首先由于搜集数据较少，所以有一定的局限性。其次，本文主要针对传媒行业搜集的数据，对其他行业的是否具有普适性还有待进一步探讨。最后，本文在探讨二次函数是否为最优模型时，仅与一次函数、三次函数、指数函数以及对数函数做了对比，对比的函数种类较少，结论可能具有片面性。财