微结构阵列超精密车床快刀伺服装置及试验研究*

关朝亮，刘俊峰，李 飞，王贵林

(1. 国防科技大学 智能科学学院， 湖南 长沙 410073； 2. 湖南航天环宇通信科技股份有限公司， 湖南 长沙 410205)

微透镜阵列、辊子表面微结构、衍射元件和全息透镜等新型微光学元件在光学薄膜、原子光学、异形靶以及通信与显示设备等领域的应用需求越来越大，这些零件表面轮廓大多为非对称的复杂面形且精度要求高，模仿形加工、研磨抛光等传统加工方法加工精度低且难以满足技术指标，更难以在曲面上制作混合光学元件；而刻蚀、激光束直写、LIGA(lithographie galvanoformung abformung)等现代加工技术对设备和材料要求高，加工一致性较差且刻蚀图形边缘不清晰，同时会对环境造成一定的污染[1]。

目前，基于超精密车削技术衍生的飞刀切、慢刀伺服和快刀伺服(Fast Tool Servo, FTS)是加工微结构阵列的主要技术，其中FTS加工的机床系统主要控制主轴和刀具进给轴运动，FTS控制系统独立于机床控制系统，各轴运动相对独立，使用条件门槛低[2]，且一次加工便可获得很高的尺寸精度和形状精度，加工效率和柔性化程度高，经济效益明显，是目前最常见的微结构阵列加工技术[1]。

国内外学者针对FTS加工技术进行了大量的研究。21世纪初，美国哥伦比亚大学的Altintas等研制的FTS系统采用压电陶瓷作为驱动器并设计了刚度为23 N/μm的柔性铰链，在普通计算机数控(Computerized Numerical Control, CNC)车床上实现了轴的精密加工[3-4]。McCall等研制了频响为1 000 Hz的FTS系统，结合Nanoform 350超精密车床在不同材料圆柱面上进行了各种微结构加工，PV值可达30 μm[5-6]。新加坡国立大学机械工程系针对金刚石车削FTS系统加工微结构提出切削力线性误差表面分析模型，并通过轮廓误差补偿将微结构表面加工进度提升至1 μm[7-8]。东京大学的Chen等通过传感器监控FTS系统加工过程中的高刚性力，结合分子动力学仿真方法优化了工艺参数，并成功地应用到脆性材料的加工中[9-10]。韩国釜山大学的Lu等发现切削速度和陶瓷驱动频率是影响FTS系统加工微结构质量的重要因素，并对加工出的微结构进行了建模与评价[11-12]。压电驱动型FTS系统已被国外Precitech、Kinetic Ceramics等公司商业化，且针对相关技术对我国大陆地区实行封锁。南京理工大学的Zhu等通过监控FST系统加工微结构过程中的切削力优化工艺参数，有效地提高了加工精度[13]。国防科技大学杨海宽利用自主研制的FTS对各种端面微结构开展了理论与试验研究，在口径4 mm、深度10 μm且呈圆周排列的微透镜阵列表面上实现了Ra11.4 nm的表面粗糙度[14]。湖南航天环宇通信科技股份有限公司的王贵林通过误差纠正方法有效地提高了FTS系统加工透镜阵列的精度，深度误差PV值高达0.06 μm[15]。浙江科技学院吴礼琼等设计了三自由度的FTS刀架，并通过有限元仿真证明了该刀架满足车削加工要求[16]。

以上工作主要研究FTS结构设计以满足加工需求，对于系统机械和电路系统性能对加工性能的影响则鲜有研究。鉴于此，本文建立了FTS系统机电耦合模型，通过参数优化研制了高性能FTS装置，并通过微结构加工实验验证了该装置的可靠性，为高性能FTS系统设计提供了依据。

1 FTS系统机电耦合模型建模与分析

1.1 建模

目前比较成熟的FTS系统大多采用压电陶瓷作为驱动元件，其工作原理如图1所示[17]，图中Uc、Ue分别为控制电压与陶瓷输入电压，R、C分别为压电陶瓷等效电阻和电容，P为增益放大器的放大倍数，kp、bp分别为压电陶瓷刚度和阻尼，Z0、Z分别为压电陶瓷实际和理论输出位移，k、b分别为柔性铰链刚度和阻尼，M为系统运动部分质量，F为压电陶瓷驱动力。

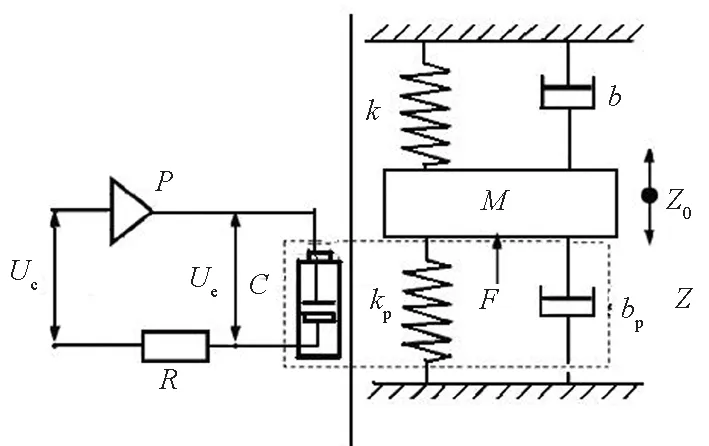
图1 FTS系统工作原理Fig.1 Function diagram of FTS system

图1右半部所示的FTS系统机械部分可视为质量-弹簧-阻尼系统，其运动方程为：

(1)

左半部电路系统的平衡方程为：

(2)

FTS系统输入为Uc，输出为Z0，将式(1)、式(2)作Laplace变换，可得到系统的传递函数为：

(3)

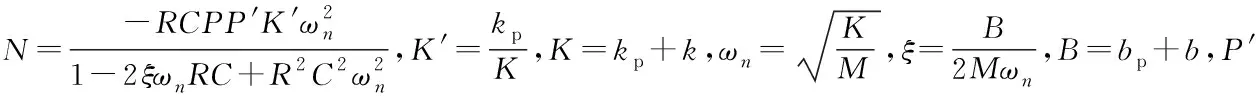
对式(3)进行Laplace反变换可得FTS系统的阶跃响应表达式为：

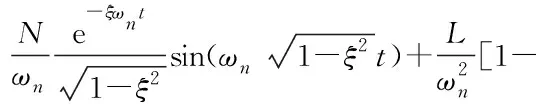
(4)

式中：φ=arccosξ。给电路系统阶跃输入，其输出响应会有延迟，定义时间常数τ为RC，则输出延迟随着时间常数的增大而增大，其最终稳态值为PP′。

故该系统阶跃响应的稳态值为：

(5)

最终稳态误差为：

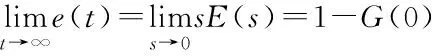
(6)

从式(4)可以看出，FTS系统阶跃响应由三个环节组成，第一部分为绕零点的衰减振荡环节，第二部分为二阶机械系统环节，第三部分为电路系统分压环节。

1.2 分析

设定M=0.1 kg，B=2 kg/s，K=280 N/μm，RC=0.001 ΩF为基准，只变动模型中某一个参数数值而其他参数不变，可得到该参数对机电耦合系统各环节阶跃响应的影响，如图2～5所示。

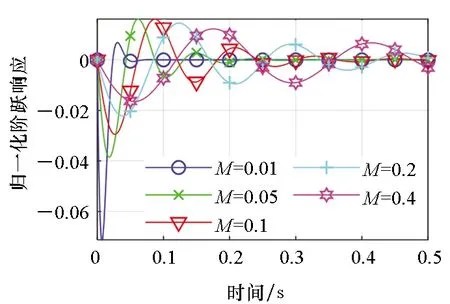
(a) 第一环节(a) The first part

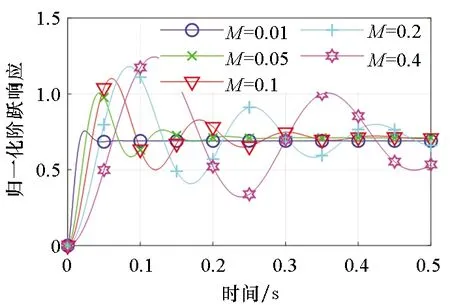
(b) 第二环节(b) The second part

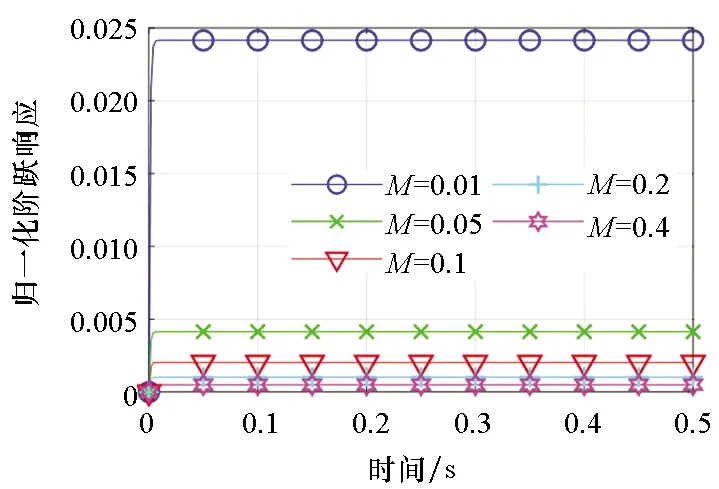
(c) 第三环节(c) The third part

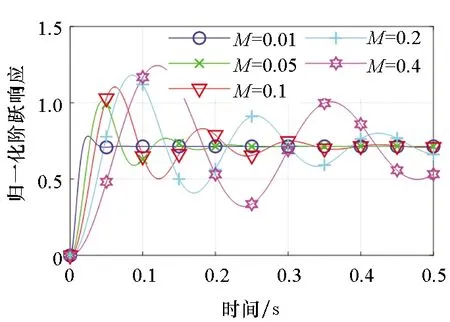
(d) 全部环节(d) All parts图2 M对系统阶跃响应的影响Fig.2 Influences of M on the step response of system

(a) 第一环节(a) The first part

(b) 第二环节(b) The second part

(c) 第三环节(c) The third part

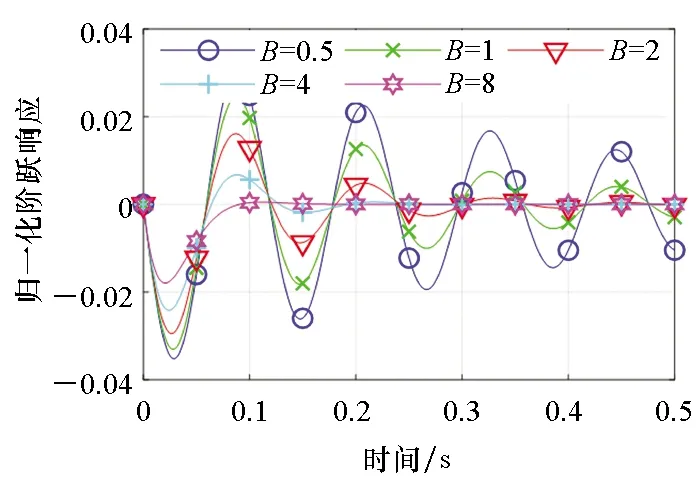
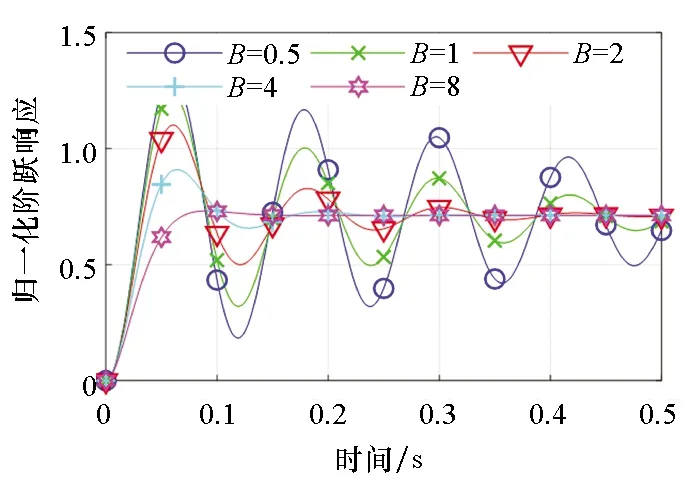
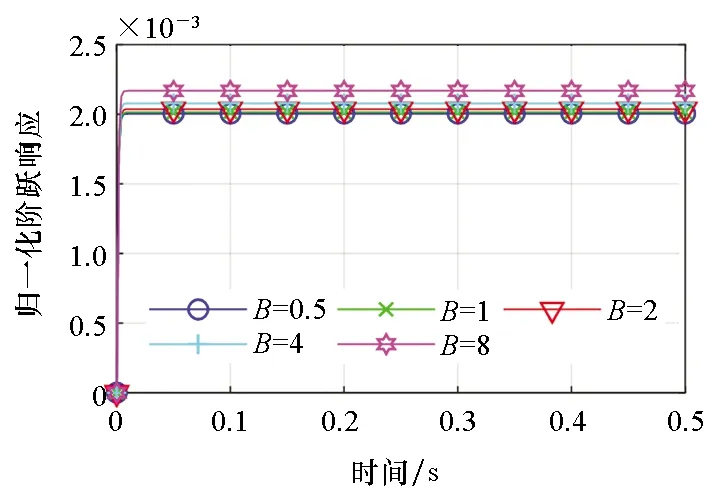
(d) 全部环节(d) All parts图3 B对系统阶跃响应的影响Fig.3 Influences of B on the step response of system

结果表明，运动质量M对系统第一环节(衰减振荡环节)影响体现在衰减速度上，增大质量衰减速度减慢，则第一环节的阶跃响应逼近稳态值零的时间增长，见图2(a)；质量较小时，第二环节(二阶机械系统环节)快速上升达到稳态，质量增加则达到稳定的时间增长，见图2(b)；质量大小对第三环节(电路系统分压环节)总体影响较小，质量越大，此环节越短，对总体阶跃响应的影响可以忽略，见图2(c)。

(a) 第一环节(a) The first part

(b) 第二环节(b) The second part

(c) 第三环节(c) The third part

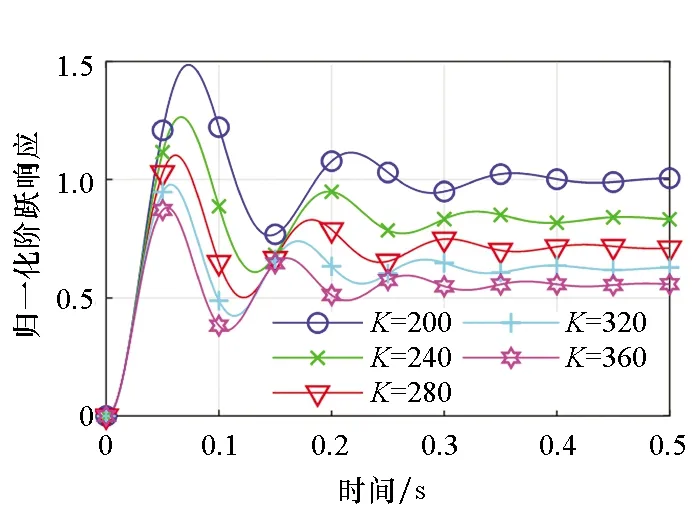
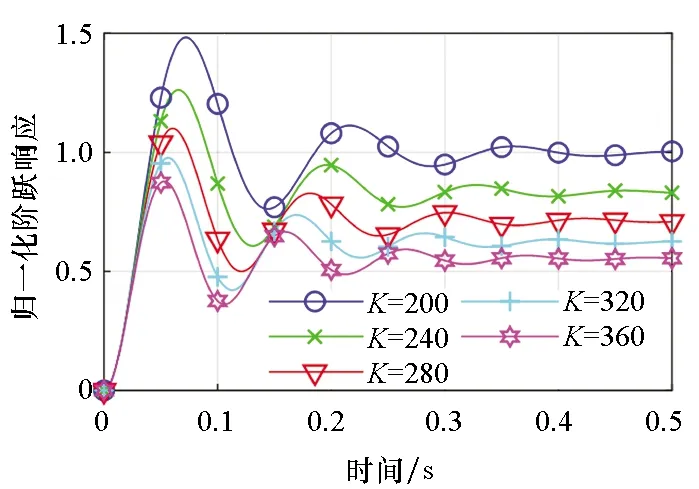
(d) 全部环节(d) All parts图4 K对系统阶跃响应的影响Fig.4 Influences of K on the step response of system

(a) 第一环节(a) The first part

(b) 第二环节(b) The second part

(c) 第三环节(c) The third part

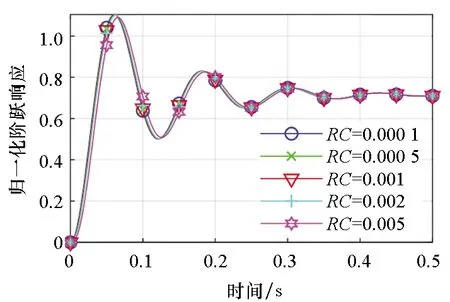
(d) 全部环节(d) All parts图5 RC对系统阶跃响应的影响Fig.5 Influences of RC on the step response of system

除第一环节外，系统阻尼B对各环节阶跃响应的影响与运动质量类似。增大阻尼则第一环节的阶跃响应快速逼近稳态值零，见图3(a)；阻尼较小时，第二环节快速上升达到稳态，阻尼增加则达到稳定的时间增长，见图3(b)；阻尼大小对第三环节总体影响较小，影响小于0.25%，对总体阶跃响应的影响可以忽略，见图3(c)。

刚度K对第一环节衰减振荡周期有一定影响，但不大，见图4(a)；对第二环节影响较大，刚度越大阶跃响应的稳态值越小，稳态误差越大，见图4(b)；对第三环节总体影响较小，影响小于0.25%，对总体阶跃响应的影响可以忽略，见图4(c)。

时间常数τ，即RC对第一环节的影响小于1%，见图5(a)；对第二环节的影响也不大，当τ≤0.002时，第二环节的阶跃响应曲线几乎重合，见图5(b)；主要对第三环节产生影响，RC越大第三环节阶跃响应的稳态值越大，见图5(c)。

实际工程中，通常将时间常数设置得比较小，以利于跟踪响应，这时整个系统主要由机械部分呈现阶跃响应，见图2～5的子图(b)、(d)。

2 柔性铰链优化设计

在FTS系统中，压电陶瓷与刀具之间通常通过刀架进行力与运动的传递，设计的刀架既能保证压电陶瓷位移精确输出，又能有效地保护压电陶瓷使其不被损坏。目前FTS系统大多采用柔性铰链作为刀架结构。铰链刚度太大会“吃掉”压电陶瓷的输出位移，太小则容易在刀具回程中造成陶瓷与铰链分离，因此铰链刚度应在满足需求的范围内结合工况而定，工作频率高则在范围内越大越好，工作频率低则在范围内越低越好，一般采用直梁型的柔性铰链来进行刚度优化[1]。

图6所示为单个直梁型铰链受力示意图和刀架运动简图，铰链在驱动力F的作用下主要产生绕z轴的弯转变形α和沿y轴的线性变形Δy。图中Rb表示铰链中过度圆弧处的半径，l为两圆弧中间直梁的长度，h、w分别为直梁厚度和铰链宽度，M′为铰链承受的弯矩。

图6 单个直梁型铰链受力示意图Fig.6 Force diagram of single straight beam hinge

根据理论分析结果和加工需求选择P225.4S型号压电陶瓷，铰链结构整体结构跟文献[14]中的铰链一致，以铰链刚度为优化目标，采用有限元仿真方法对直梁长度和最小厚度进行优化，其余参数与文献[14]中一致。

图7为直梁长度和最小厚度对铰链刚度的影响，由图可知，直梁长度越大，铰链刚度越小；最小厚度越大，铰链刚度越大。根据加工需求选定直梁长度为7 mm，最小厚度为0.6 mm。

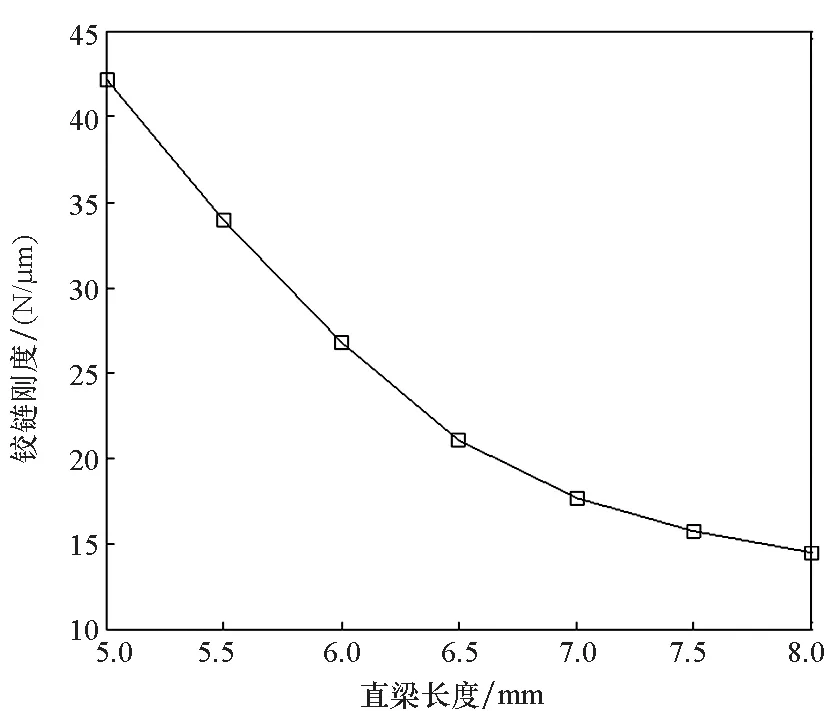
(a) 直梁长度影响(a) Effect of the length of straight beam

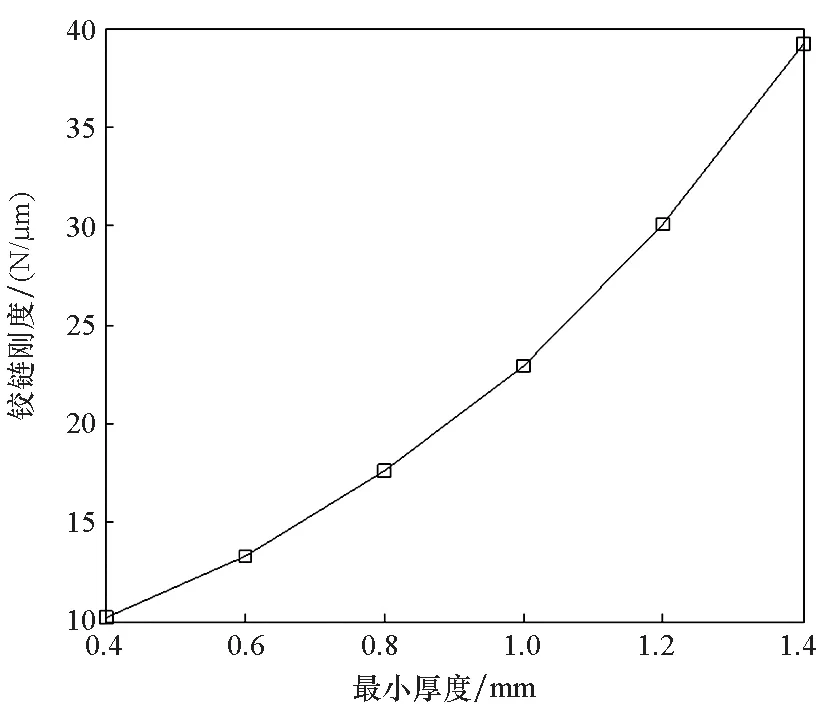
(b) 最小厚度影响(b) Effect of the minimal thickness图7 直梁长度和最小厚度对铰链刚度的影响Fig.7 Influences of length of straight beam and minimal thickness on the hinge stiffness

优化后的铰链最大工作位移下的范式应力以及一阶振型如图8所示。由图可知，与刀具相连接的运动块位移40 μm时铰链最大范式应力为0.157 GPa，远小于铰链材料60Si2Mn的屈服极限1.176 GPa；铰链一阶固有频率为2 552.4 Hz，远高于系统最高工作频率1 000 Hz。

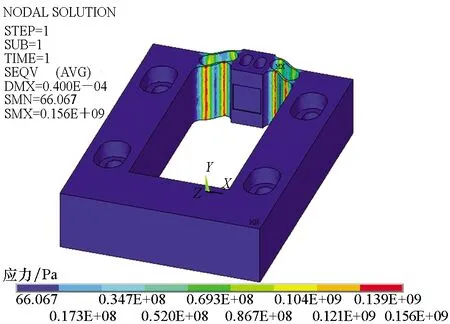
(a) 范式应力分布(a) Paradigm stress distribution

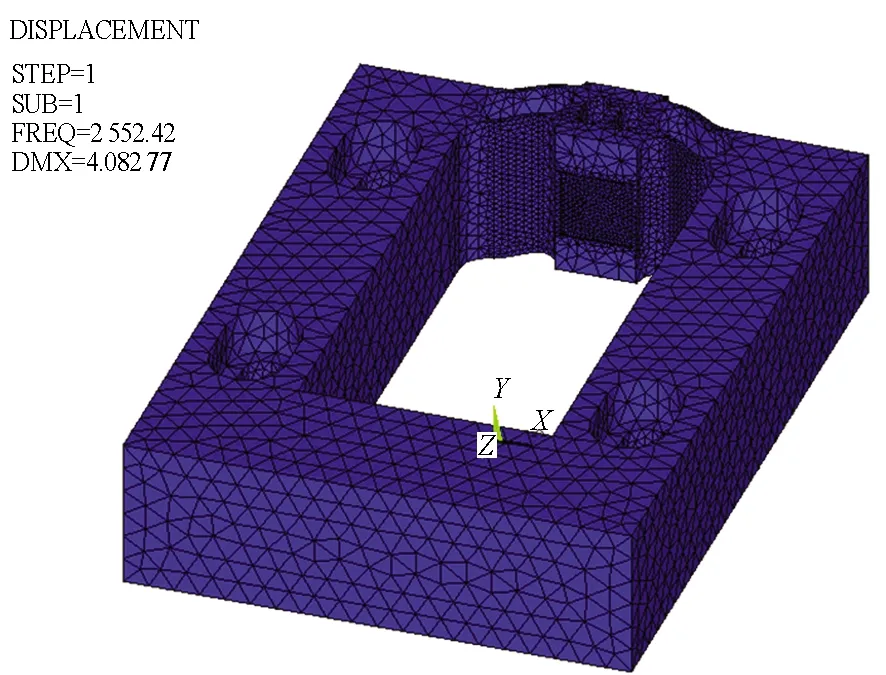
(b) 一阶振型(b) First-order vibration type图8 应力与一阶振型仿真Fig.8 Simulations of stress and first-order vibration type

3 测试与加工试验

3.1 线性度测试

为测量FTS装置输出位移的线性度，对系统电源输入等间隔递增的控制电压，用Keyence的激光位移传感器测量刀架前端位移。该传感器采样频率高，方便固定而减小环境振动干扰，分辨率为10 nm；为提高测量精度，传感器设置成截止频率5 Hz的低通滤波形式以降低噪声影响[17]。表1为输入电压为1～6 V时测得的刀架前端位移，相同输入电压重复测量三次刀架前端位移。测试结果表明研制的FTS装置输出位移线性度误差优于0.5%，重复定位误差优于20 nm，具备良好的静态输出性能。

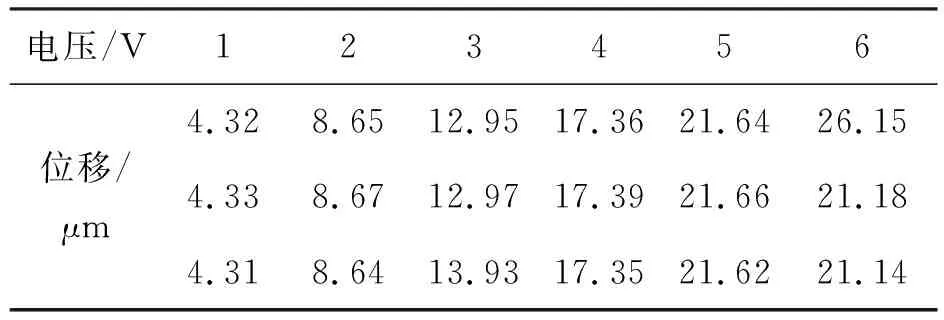
表1 FTS装置输出位移Tab.1 Output displacements of FTS device

3.2 正弦网格微结构加工试验

正弦网格微结构沿机床X轴方向的切削深度tX的方程为：

(7)

式中：As、AZ分别为周向和轴向幅值；λs、λZ分别是周向和轴向周期；Rw为工件半径，θ为主轴转角；tZ为切削点的轴向位置。

以红铜材料圆柱工件为加工对象，在其圆柱面不同段分别加工正弦网格微结构。表2所列的是试验参数。

表2 正弦网格试验参数Tab.2 Test parameters of sinusoidal grids

按表2试验参数加工后，利用轮廓仪PGI1240沿工件轴向测量一条过正弦阵列最高和最低点的轮廓线(见图9)，评价正弦阵列的加工情况。前4 mm为第一段，进给速度为0.2 mm/min；后4 mm为第二段，进给速度为0.1 mm/min。图9中将轮廓测量数据的高频成分(对应粗糙度轮廓)提取出来，可知微结构加工进给速度fZ越小，其轮廓粗糙度也越小。统计分析第一和第二段各4个周期的节距误差，如图10所示，可知微结构加工进给速度越小，节距误差越小且更稳定。

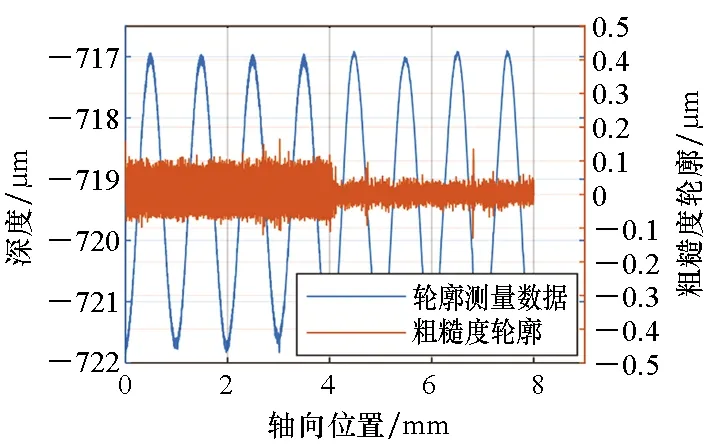
图9 轮廓仪测得的轴向轮廓Fig.9 Axial outline measured by profilometer

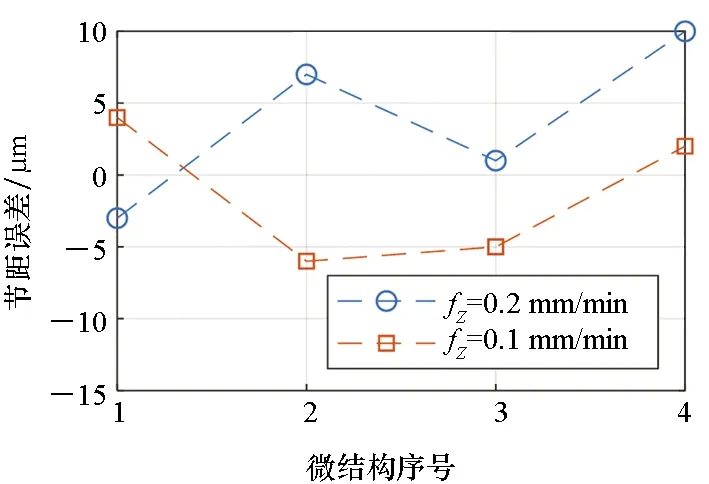
图10 节距点节距Fig.10 Varieties of pitch at pitch points

图11所示的是两段微结构第一个周期轮廓曲线，表明不同进给速度下理论曲线峰谷值相对实测曲线较小，但趋势吻合，误差主要来自系统的控制误差和振动及其作用力。第一个周期轮廓深度方向的误差如图12所示，可知进给速度越大，机床X方向(深度方向)的误差越大，这是因为大的进给速度会带来更大的切削作用力，导致振动加剧。因此在满足效率要求的前提下，Z轴进给速度应尽可能小。图13为加工出的正弦微结构。

(a) fZ=0.1 mm/min

(b) fZ=0.2 mm/min图11 两段微结构第一圈单个轮廓Fig.11 Single outlines of the first circle of two segments microstructures

(a) fZ=0.1 mm/min

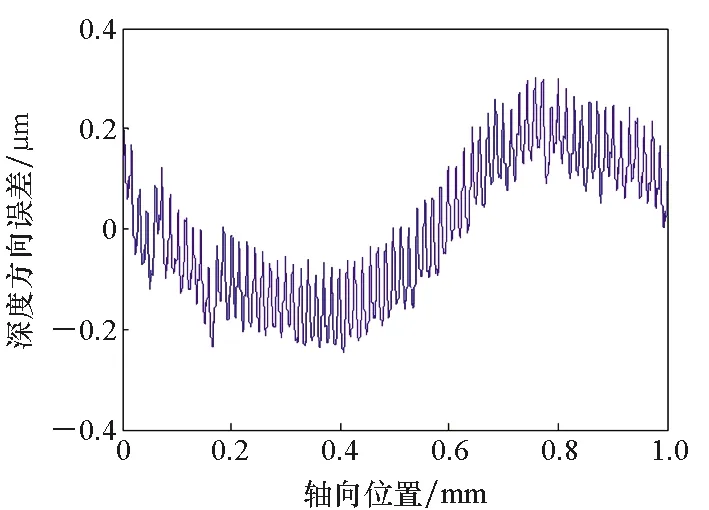
(b) fZ=0.2 mm/min图12 不同进给速度对应的单个轮廓深度方向误差Fig.12 Errors in the depth direction of single outlines with different feed speeds

图13 加工实物Fig.13 Manufactured material object

4 结论

对压电陶瓷驱动的FTS系统进行了机电耦合建模预分析，通过有限元方法对刀架铰链进行了结构优化，并基于研制的FTS装置进行了正弦网格微结构加工，理论和实验结果表明：

1)对于压电陶瓷驱动的FTS系统，选取RC值较小的压电陶瓷驱动器，运动质量越小越好，系统刚度、阻尼则视工况而定。

2)对于直梁型铰链，铰链刚度随着最小厚度的增大而增大，随直梁长度的增大而减小。

3)根据优化参数研制的FTS装置能够准确有效地加工出正弦网格等复杂微结构，可指导高性能FTS系统设计。